基于支持向量回歸積和改進粒子群算法的特定區間盾構機作業參數選取

許哲東 侯公羽 楊 麗 黃小軍

1.安徽工程大學建筑工程學院，蕪湖，2410002.中國礦業大學(北京)力學與建筑工程學院，北京，100083

0 引言

在盾構機施工過程中，掘進參數對地表沉降有著非常重要的影響[1],如何選取最佳掘進參數是一個需要不斷研究的課題。以地表沉降值為控制目標，掘進最優參數的選取包括非線性關系模型的建立和參數優化，非線性建模和優化方法的性能直接影響參數選取的準確性和可靠性。學者們采用了不同的方法來解決此類問題。基于對所選參數的分析，MOEINOSSADAT等[2]應用神經模糊推理系統建立所選參數與地面沉降值之間的非線性關系，通過不斷更改選定的參數值，使地面沉降值最小化。李杰等[3]為在確保開挖面穩定的基礎上提高實際施工現場盾構機掘進效率，進行了正交試驗，同時，建立了掘進速度與掘進參數之間的數學模型，在MATLAB中對隧道參數進行了優化。曹曦等[4]分析了密封艙土壓與掘進參數的關系，并采用最小二乘支持向量機建立了土壓預測模型，同時基于粒子群算法實現了掘進參數的在線優化。羌培[5]針對超大直徑的掘進參數匹配問題，采用BP神經網絡模型建立了各盾構施工參數與隧道軸線上方地表沉降值之間的關系，再采用遺傳算法實現了參數尋優。

學者們在一定程度上采用了不同的方法實現掘進參數匹配，但是，隨著施工復雜度的提高，傳統的參數選取方法難以實現，另外，隨著工程項目越來越復雜，考慮的因素越來越多，對數據挖掘技術的性能要求也越來越高，在解決實際問題時，由于數據的不同特點，數據挖掘方法應用的性能也存在差異。因此，在目前盾構直徑以及深度在逐漸增大的情況下[6]，如何提高特定區間掘進參數選取的準確性和可靠性是一個需要研究的問題。本課題從掘進參數選取中非線性建模和參數優化兩個方面分別進行研究。

對于難以準確建立數學表達式的非線性關系建模，通常采用機器學習方法，如支持向量回歸積(e-support vector regression，e-SVR)、隨機森林(random forest，RF)和人工神經網絡(artificial neural network，ANN)[7-9]，這些方法各有優缺點，在解決實際問題時，有必要根據具體問題分析選擇最佳方法。為了更準確地實現特定區間掘進參數的選取，同時考慮地層參數、幾何參數、掘進參數與地表沉降值之間的非線性關系，建立盾構機作業參數非線性關系模型。以實際盾構施工數據為基礎，分析e-SVR、RF和ANN模型性能，得到建立盾構機作業參數非線性關系模型的最佳方法。

對于工程參數優化，智能算法是首選，它為各個行業提供了很多有效的解決方案。智能算法包括退火算法[10]、PSO算法[11]和遺傳算法[12]等，其中，PSO算法廣泛應用于許多領域[13-14]，但是，研究表明，標準PSO算法存在一些缺陷，很多學者對標準PSO算法進行了改進。SHI等[15]提出了一種線性遞減的慣性權重調整等式，且給出了權重取值范圍0.4～0.9。韓江洪等[16]為了降低算法出現“早熟”現象的概率，提出一種自適應調整慣性權重的PSO算法。封京梅等[17]為了求解不可微的NP難的絕對值方程問題，結合指數函數的曲線特征，提出了慣性權重指數遞減的策略。根據學者們的研究得出慣性權重在迭代前期應取較大值，在迭代后期應為較小值的結論，然而，學者們并沒有研究在迭代過程中，慣性權重下降速度對PSO算法性能的影響，因此，本文基于指數遞減調整等式，采用指數函數中不同指數形式來控制迭代過程中慣性權重的下降速度，通過仿真實驗，分析慣性權重降低速度對PSO算法性能的影響。根據實驗結果，提出一種改進慣性權重降低速度粒子群優化(improved inertia weight decreasing speed particle swarm optimization，IIWDSPSO)算法。最后，基于e-SVR和改進粒子群算法實現對特定地層參數和幾何參數區間的掘進參數優化選取。

1 PSO算法及其慣性權重降低速度仿真實驗

PSO算法是模擬鳥群覓食的過程[18]。在迭代過程中，粒子速度和位置主要由兩個最佳位置更新，包括粒子個體最佳位置和所有粒子中全局最佳位置。速度和位置由下式更新[19]：

vis(t+1)=ωvis(t)+c1r1(pis(t)-xis(t))+
c2r2(pgs(t)-xis(t))

(1)

xis(t+1)=xis(t)+vis(t+1)

(2)

式中，ω為慣性權重；r1、r2為位于(0,1)的隨機值；c1、c2為加速因子；pis為第i個粒子在第s個方向上的個體最優位置；pgs為在第s個方向上的全局最優位置；xis為第i個粒子在第s個方向上的位置；t為迭代次數。

目前學者們所研究的慣性權重調整等式主要有線性遞減調整等式：

(3)

隨機調整等式：

ω=ωmin+(ωmax-ωmin)·rand(·)

(4)

非線性遞減調整等式：

(5)

(6)

式中，ωmin為慣性權重最小值；ωmax為慣性權重最大值；rand(·)為隨機函數；t為當前迭代次數；T為總迭代次數；d1、d2為常數。

根據指數遞減函數曲線特點，可以發現這種函數曲線的變化趨勢與迭代過程中慣性權重的變化是一致的。因此，采用指數函數中不同形式的指數來控制迭代過程中慣性權重的降低速度，可以看出它對算法性能的影響。

1.1 實驗設置

根據指數遞減函數式

(7)

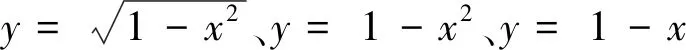
(8)

(9)

(10)

(11)

設置T為100，ωmin為0.4，ωmax為0.9，四種調整等式下慣性權重在迭代過程中的變化曲線如圖1所示。

圖1 慣性權重變化曲線

由圖1可得，式(8)對應的慣性權重值在前期下降最慢，能夠較長時間保持較大值，其次是式(9)和式(10)對應的慣性權重下降速度較慢，式(11)對應慣性權重值在早期階段下降最快。保持其他條件相同，采用表1中10個經典測試函數研究慣性權重降低速度對PSO算法性能的影響。

表1 10個經典測試函數

表1中f1、f2、f3、f4、f5為單峰值函數，只有一個最優值，f6、f7、f8、f9,、f10為多峰值函數，存在局部最優值。四種不同慣性權重降低速度對應算法分別對每個函數獨立運行20次。評價算法性能的指標有：20次運行的最小值、平均值、均方根誤差(RMSE)和收斂目標完成率。實驗參數設置如下：T=100，ωmin=0.4，ωmax=0.9，學習因子c1和c2為2，粒子種群規模為50。使用四種不同慣性權重降低速度的粒子群優化算法分別對10個函數進行優化,最終實驗結果如圖2～圖5所示。

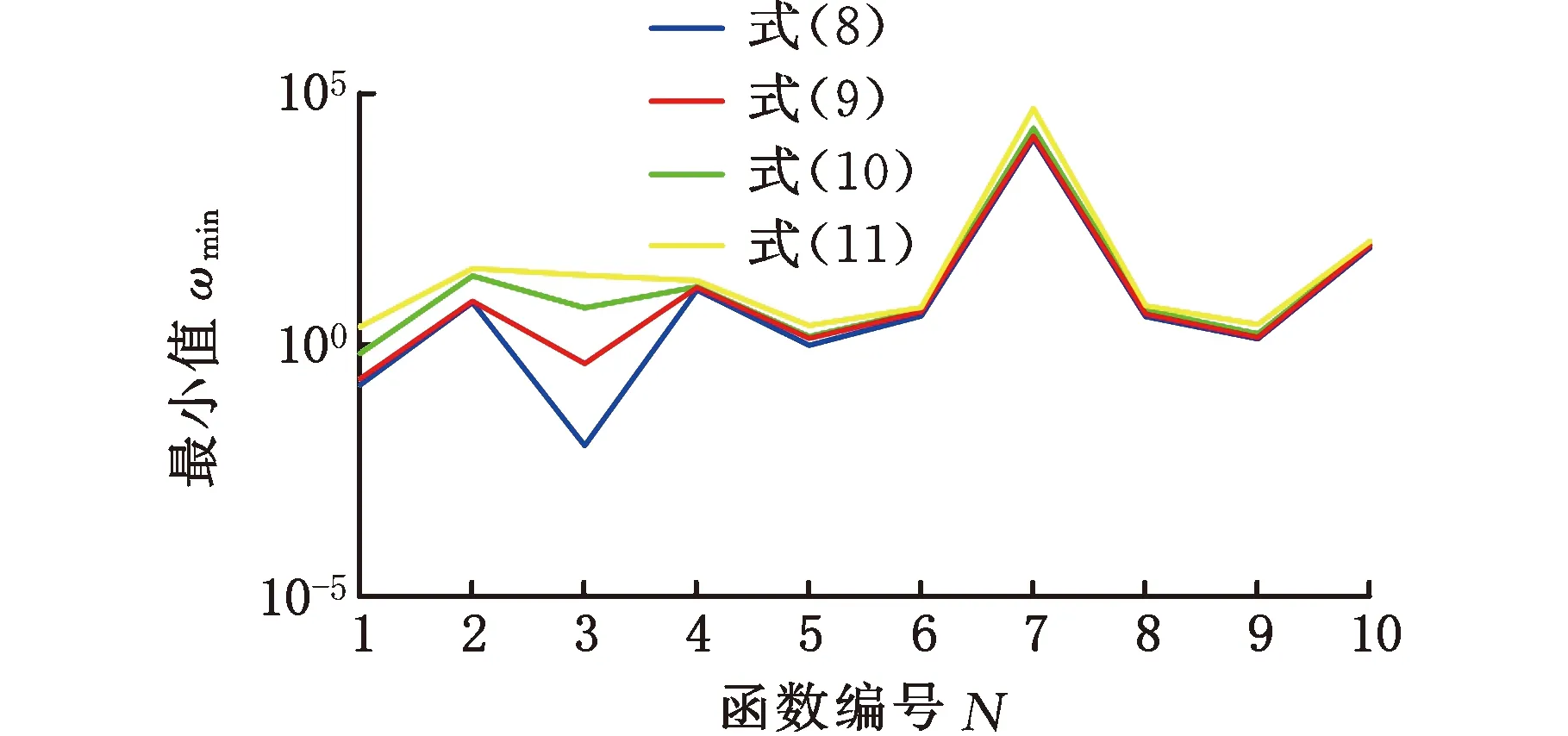
圖2 20次獨立運行的最小值

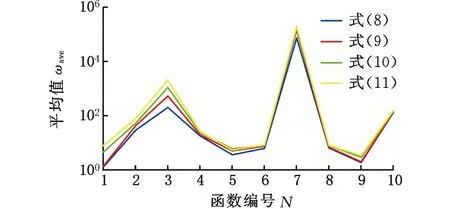
圖3 20次獨立運行的平均值

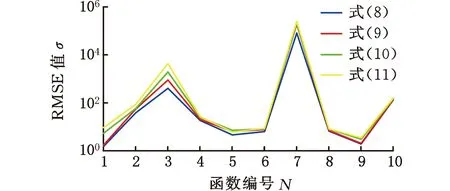
圖4 20次獨立運行的RMSE

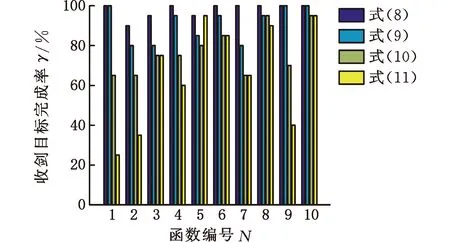
圖5 收斂目標完成率

1.2 實驗結果分析

由圖2可知，四種不同慣性權重降低速度的算法對單峰值和多峰值函數20次獨立運行的最小值折線從低到高依次是式(8)、式(9)、式(10)和式(11)。與求解單峰值函數實驗結果相比，四種不同慣性權重降低速度的算法求解多峰值函數得到的最小值折線比較接近，主要原因是多峰值函數中存在多個局部極值，因此獲得全局最優值的難度更大。圖3中，除了式(11)對應算法在f5函數中獲得的尋優平均值低于式(10)對應算法尋優平均值外，在其他函數中，式(8)～式(11)對應算法獲得的尋優平均值從小到大排序為：式(8)、式(9)、式(10)、式(11)。結果表明，在迭代初期，慣性權重下降速度越慢，算法優化單峰值和多峰值函數的準確性越高。

RMSE值是一個評價穩定性的指標。由圖4可知，僅函數f5中式(11)對應算法尋優的RMSE值小于式(9)和式(10)對應算法尋優的RMSE值，但仍大于式(8)對應算法尋優的RMSE值。在其他函數中，RMSE值從小到大排列為：式(8)、式(9)、式(10)、式(11)。RMSE值表明在迭代初期慣性權重下降速度越慢，PSO算法在求解單峰值和多峰值函數中的穩定性越好。

根據圖5中的收斂目標完成率條形圖可得，除了f5，其他函數中收斂目標完成率值γ均滿足γeq.(8)≥γeq.(9)≥γeq.(10)≥γeq.(11)，因此，從整體數值規律可以得出，在前期迭代中慣性權重下降速度越慢，收斂目標完成率越高。

由四種不同慣性權重降低速度對應算法在單峰值和多峰值函數中的性能分析可得，迭代前期慣性權重降低速度越慢，PSO算法精度、穩定性、收斂目標完成率越好。因此，基于實驗結果，當采用指數遞減函數式(7)的形式調整慣性權重時，指數x的最佳形式是圓心為0、半徑為1的圓形公式，因此基于此提出了IIWDSPSO算法。

2 基于e-SVR和IIWDSPSO的特定區間盾構機作業參數選取模型

2.1 基于e-SVR的盾構機作業參數非線性關系建模

以地表沉降值作為控制目標，建立掘進參數、地層參數、幾何參數與地表沉降值之間的非線性關系模型。掘進參數、地層參數與幾何參數數值組成輸入變量X，對應的地表沉降值作為輸出變量yi。將訓練樣本映射到一個高維(l維)特征空間，采用下式線性回歸：

f(X)=WTφ(X)+b

(12)

式中，W為l維權重向量；φ(X)為高維空間映射函數；b為偏置項。

基于ε不敏感損失函數，將回歸問題轉化求最優值問題：

(13)

約束條件為

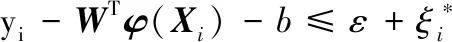
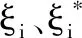
將以上優化形式進行轉化：

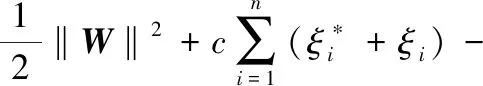
(14)

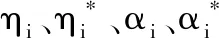
對式(14)中W、b、ξ、ξ*求偏導，且令其為零，得

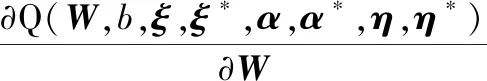
(15)

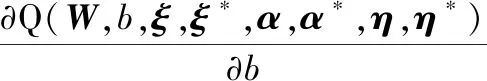
(16)

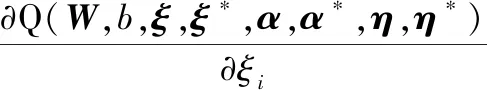
(17)

(18)

將式(15)～式(18)代入式(14)中，得其對偶問題：

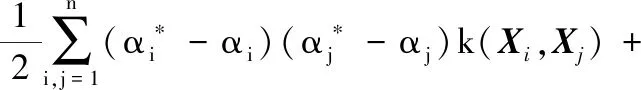
(19)

約束條件為

基于實際盾構施工參數數據，求得最優解：

(20)

偏置項b通過卡羅需-庫恩-塔克條件求解：

(21)

(22)

2.2 IIWDSPSO算法優化特定地層參數和幾何參數區間的掘進參數

基于e-SVR構建的能夠表達幾何參數、地層參數、掘進參數與地表沉降值之間非線性關系的模型，以地表沉降值最小為優化目標，運用IIWDSPSO算法對特定幾何參數和地層參數的區間掘進參數進行優化。

首先設置慣性權重的ωmin和ωmax，加速因子c1和c2，最大迭代次數T以及種群規模M。粒子空間位置向量由掘進參數、幾何參數和地層參數構成，假設掘進參數、幾何參數和地層參數共q個，則每個粒子空間位置Xs=(xs1,xs2,…,xsq)(s=1,2,…,M)。初始化算法迭代過程中掘進參數變化值作為粒子速度Vs=(vs1,vs2,…,vsq)(s=1,2,…,M)。注意，幾何參數和地層參數是人為無法改變的量，因此，對應方向的速度需設為0。

根據最終訓練得到的e-SVR模型計算IIWDSPSO算法中每一個粒子的適應度值，粒子j(j=1,2,…,M)的適應度ffit計算為

(23)

ffit(s)=1/f(Xs)

(24)

將初始化的粒子位置分別作為第一次迭代之前的每個粒子的個體極值Ps=(p1,ps2,…,psq)=(xs1,xs2,…,xsq)(s=1,2,…,M)，其中適應度值最大的粒子g的位置作為群體極值Pg=(pg1,pg2,…,pgq)=(xg1,xg2,…,xgq)。通過式(1)和式(2)更新迭代，慣性權重調整等式采用式(8)，循環迭代直到滿足最大迭代次數結束。

3 基于實際盾構施工數據的模型驗證

3.1 基于e-SVR構建的盾構作業參數非線性關系模型實際性能

結合實際工程盾構施工數據，對e-SVR建立的幾何參數(深跨比H/D)，地層參數(水位d和重度W)，掘進參數(扭矩T0、總推力F、土艙壓力ps、出渣量V、注漿量S和貫入度C)與地表沉降值h之間的非線性模型進行訓練和測試，與此同時，和RF和ANN模型進行對比分析。施工數據來源于長株潭城際鐵路工程項目[20]。所選參數和相應的樣本數據折線圖見圖6～圖8所示。

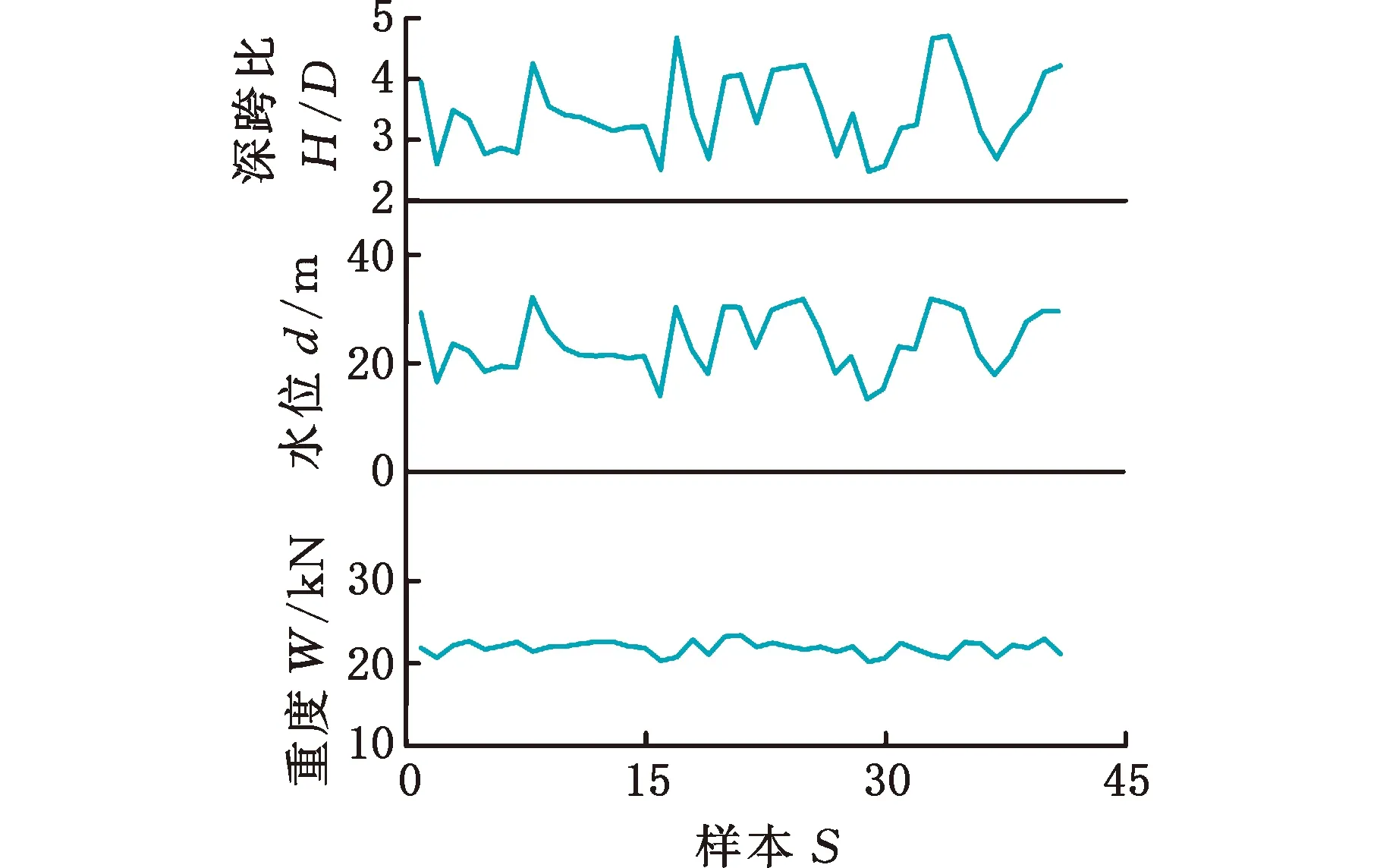
圖6 41組幾何參數值和地層條件參數值

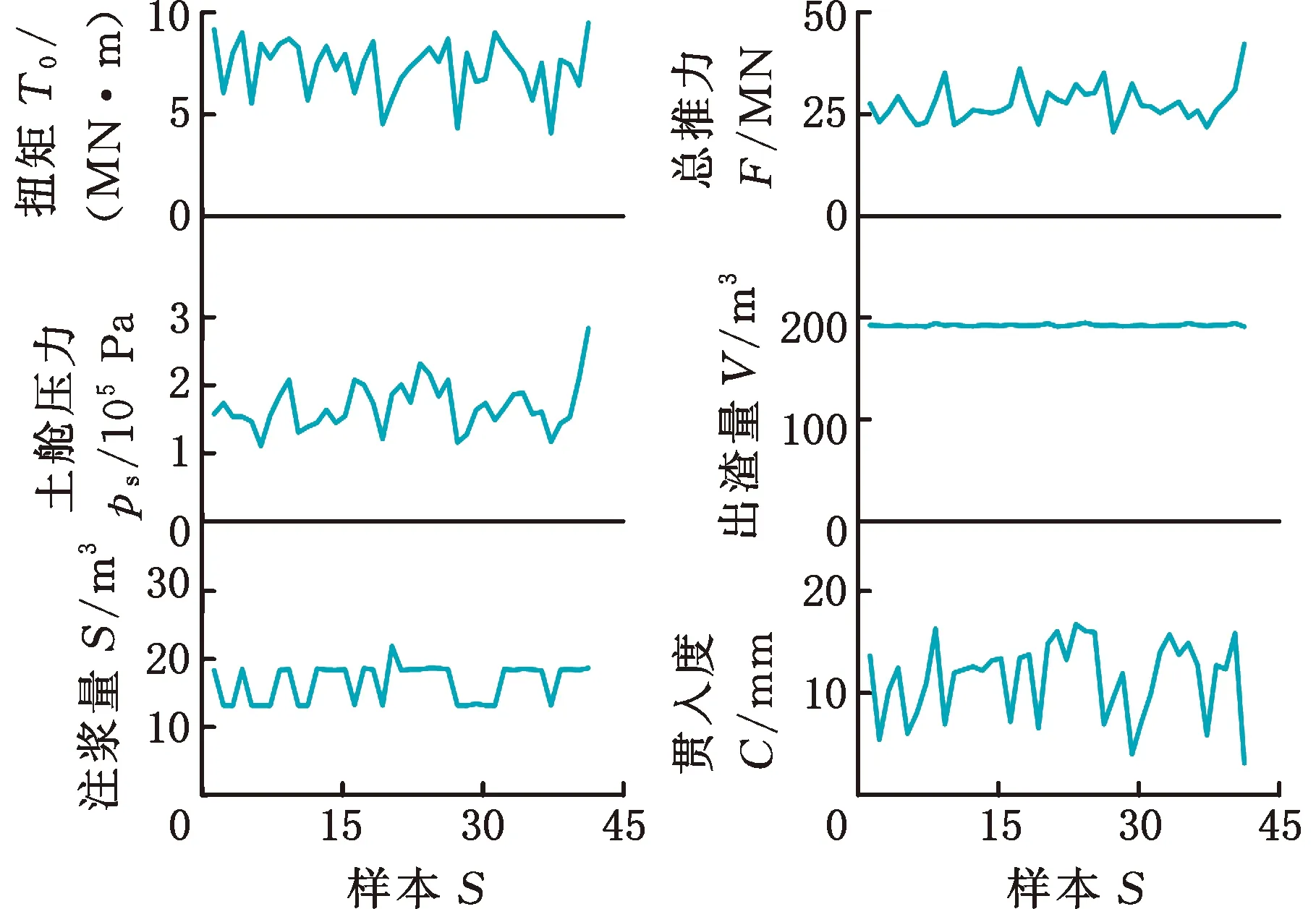
圖7 41組掘進參數值

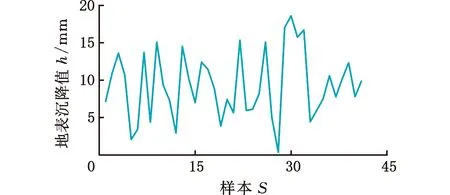
圖8 41組地表沉降值

將圖6和圖7中前37組幾何參數、地層參數和掘進參數作為訓練輸入樣本，對應的圖8中前37組地表沉降值作為訓練輸出樣本,對e-SVR、RF和ANN模型進行訓練。在實驗中，通過反復訓練得到各模型的最優結果。最終e-SVR模型中的參數值設置如下[21]：核函數類型為RBF，懲罰參數c=1.8，核函數的系數g=1.5，損失函數值為0.0001；RF模型主要參數設置為[22]：決策樹最大深度為14，樹的數目為50，分裂邊界的個數為5；ANN模型參數值[23]：最大迭代次數為5000，學習效率為0.1。

最終得到的e-SVR、RF和ANN模型地表沉降預測值和實際值比較如圖9所示。由圖9可知，e-SVR模型中除了4個點不在直線上，其他點均擬合較好。RF模型各點基本都在直線上，而ANN模型對樣本點的擬合較差。

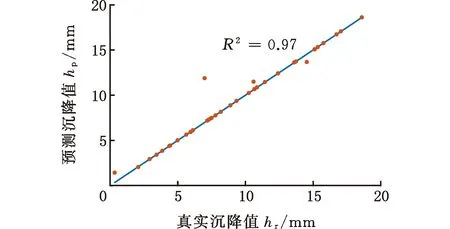
(a)e-SVR模型

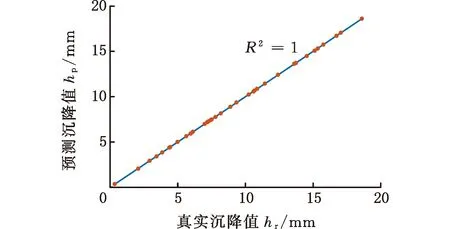
(b)RF模型

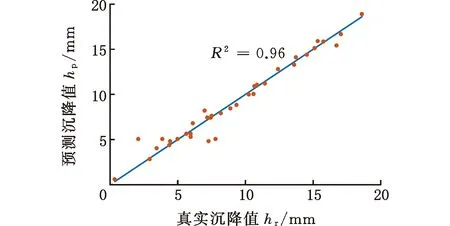
(c)ANN模型圖9 模型擬合效果

基于訓練得到的e-SVR、RF和ANN模型，使用測試集測試模型泛化能力，測試結果如表2所示。測試集中e-SVR、RF和ANN模型預測的相對誤差平均值分別為0.06、0.24和0.07。所以，e-SVR模型得到的相對誤差平均值最小。雖然RF模型對盾構作業參數樣本有很好的擬合效果，但其測試結果相對誤差平均值是最大的，表明了RF模型的泛化能力較差。因此，綜合模型對盾構作業參數樣本的擬合和泛化能力，可以得出e-SVR模型綜合性能最好的結論。

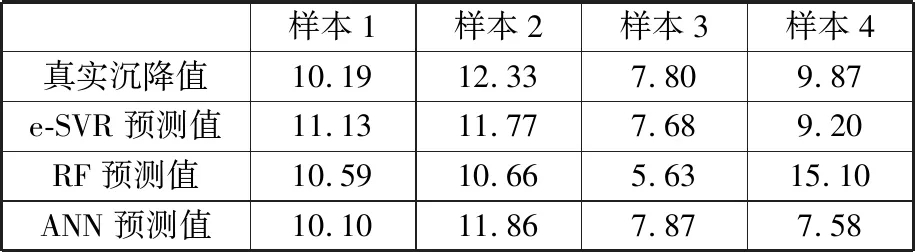
表2 測試結果

3.2 IIWDSPSO算法優化特定地層參數和幾何參數區間的掘進參數性能

基于3.1節獲得的長株潭城際鐵路工程數據建立的e-SVR模型，采用IIWDSPSO算法對幾何參數和地層條件參數值如表3所示的隧道區段掘進參數進行優化，同時，與其他三種不同慣性權重降低速度的算法進行比較，最終優化得到的地表沉降值如表4所示。

表3 幾何參數和地層條件參數值

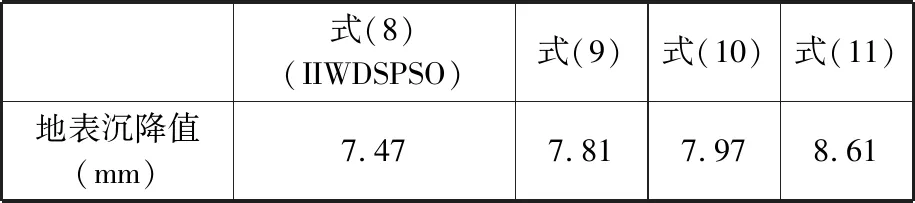
表4 優化所得地表沉降值

由表4可得，IIWDSPSO算法獲得的地表沉降值相對更小。基于IIWDSPSO算法得到的各掘進參數值分別為：刀盤扭矩值8406.99 kN·m，盾構推力值28 481.97 kN，土艙壓力值1.85×105Pa，出渣量值194.32 m3，同步注漿量值17.96 m3，貫入度值16.27。最終優化得到的地表沉降值較為接近，但是根據本文方法的性能分析可知，基于e-SVR和IIWDSPSO模型獲得的結果具有更高的可靠度。

在實際工程中，影響地表沉降的因素很多。目前，在模型中很難考慮所有因素，因此，在施工過程中，還需要根據模型得到的掘進參數值再進一步微調，模型的準確性和可靠性直接影響后期參數調整的效率。通過實驗分析，本文提出的基于e-SVR和IIWDSPSO特定區間盾構機作業參數選取模型可以為實際工程中掘進參數的選取提供更準確和可靠的方法。

4 結論

為了提高特定區間盾構機作業參數選取的可靠性和準確性，研究了優化方法中PSO算法慣性權重降低速度對算法性能的影響，并提出了改進慣性權重降低速度粒子群優化(IIWDSPSO)算法。同時考慮掘進參數、地層參數、幾何參數與地表沉降之間的非線性關系，基于實際盾構施工數據，將e-SVR與ANN、RF算法分別用于構建其關系模型并進行性能對比分析。最后基于e-SVR和IIWDSPSO算法實現特定幾何參數和地層參數區間的掘進參數優化，得出主要結論如下：

(1)以地表沉降控制為目標，基于實際盾構施工數據，分析了e-SVR、RF和ANN模型的擬合和泛化能力，結果表明，e-SVR、RF模型對盾構作業參數樣本有較好的擬合效果，但RF模型的泛化能力較差。綜合考慮模型的擬合和泛化能力，e-SVR模型是盾構機作業參數建模的最佳選擇。

(2)無論是單峰值函數還是多峰值函數，PSO算法的慣性權重在迭代初期降低速度越慢，PSO算法的優化能力越好。當采用指數遞減函數(式(7))的形式調整慣性權重時，指數x的最佳形式是圓心為0、半徑為1的圓形公式，即式(8)。

(3)基于實際工程中獲得的掘進參數、地層參數、幾何參數與地表沉降值之間的非線性關系e-SVR模型，采用IIWDSPSO算法和其他三種不同慣性權重降低速度的算法對特定地層參數和幾何參數區間掘進參數進行優化，基于IIWDSPSO算法得到的最終地表沉降值相對更小。因此，所提出的基于e-SVR和IIWDSPSO算法的特定區間盾構機作業參數選取模型可以為實際工程中參數調整提供更準確可靠的參考。