從數系的擴充談起
卞書彥
我們在七年級已經系統地學習過有理數,知道了數的擴充源于兩方面的需求:一是為了解決實際生產、生活中的某些問題;二是為了數學內部的運算可以進行(即運算的封閉性)。我們也知道了每次數系擴充遵循的基本原則:第一,增加新元素;第二,原有的運算性質仍然成立;第三,新數系能解決舊數系中的矛盾。
本章一開始以運用勾股定理計算直角三角形邊長為情境,讓我們感受到“數的開方”的必要性,順理成章地讓我們學習平方根的概念。我們在七年級就知道非完全平方數(如數2)的平方根(算術平方根)是客觀存在的,能用逼近法知道它是無限不循環小數,并能用數軸上的點將它表示出來。為了進一步研究這樣的數,我們有必要用符號來表示。法國數學家笛卡爾使用符號“[]”很好地解決了這類數的表示問題。
有了平方根概念和表示符號后,我們就可以研究其性質與應用了。根據平方與開平方互逆的關系可以得到:一個正數有兩個平方根,它們互為相反數;0的平方根是0;負數沒有平方根。我們可以類比學習三次方根的概念以及符號“[3]”所表示的意義,根據立方與開立方互逆的關系得到:正數的立方根是正數;負數的立方根是負數;0的立方根是0。同理,根據平方根與立方根的學習經驗,我們也可類比得到“n次方根”的符號“[n]”及其有關的性質了。
我們認識到,開方開不盡的數是無限不循環小數。無限不循環小數除了開方開不盡的數外,還有像化簡后含“π”的數與0.1010010001…(1后面的0依次多一個)這一類數,以后我們還會學習到其他形式的無限不循環小數。為此,我們將無限不循環小數定義為無理數,并將有理數和無理數統稱為實數。由此,我們就實現了從有理數集到實數集的擴充。
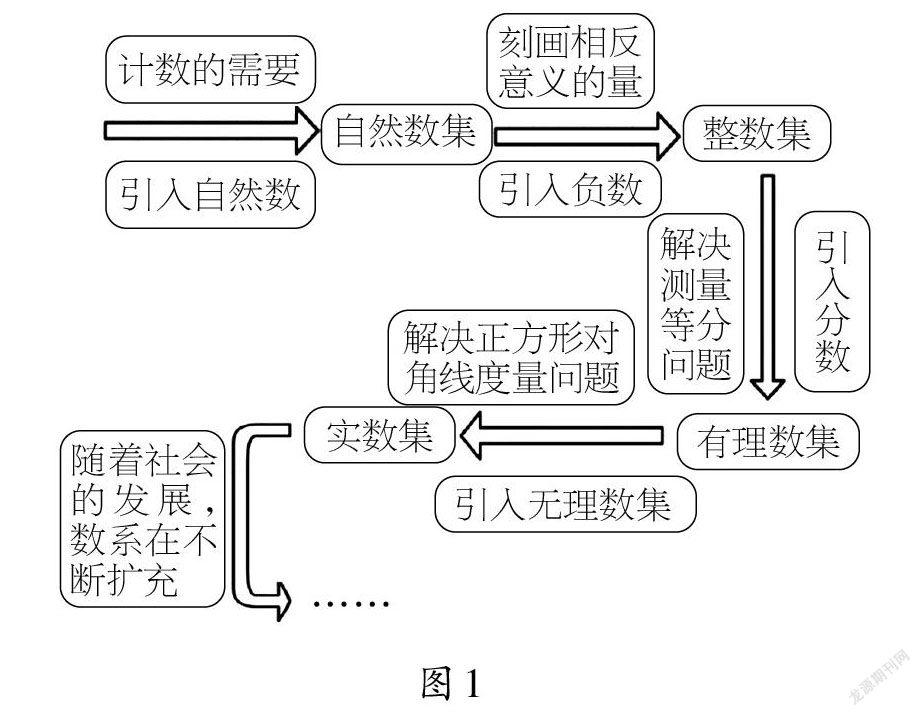
下面,我們通過圖1一起回顧一下人類對數的認識吧。
數系擴充到實數后,對有理數的絕對值、相反數、倒數的意義,有理數比較大小的方法,有理數的運算性質、運算律,仍然都適用。在實數范圍內,不僅可以進行加、減、乘、除、乘方運算,還可以進行開立方運算以及非負實數的開平方運算。
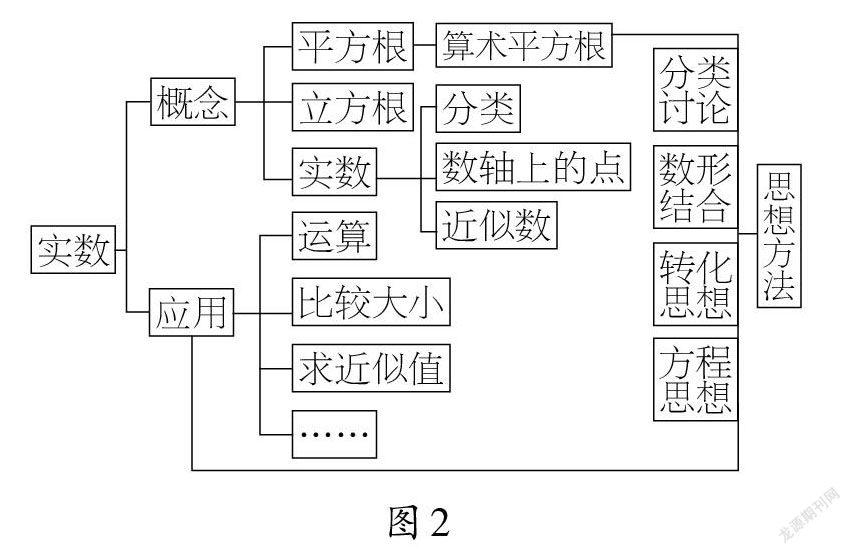
由于無理數是無限不循環小數,有時根據實際需要,我們要用它的近似值來代替。因此,我們還要了解近似數的概念,體會近似數的意義以及近似數在生產、生活中的作用,并能根據要求對結果取近似值。于是,我們得到本章的知識框圖(如圖2)。
實數這一章的知識是我們學習二次根式、一元二次方程以及解三角形等知識的基礎,為今后數系的擴充提供了范式,相信同學們一定能夠學好本章的有關內容。
(作者單位:江蘇省鹽城市大岡初級中學)

