廣義Tikhonov正則化工況傳遞路徑分析

唐中華， 昝 鳴， 張志飛， 徐中明， 晉 杰

(1. 重慶大學 機械與運載工程學院，重慶 400044； 2. 交通運輸部公路科學研究院，北京 100088)

工況傳遞路徑分析(operational transfer path analysis，OTPA)是定位與辨識振動噪聲問題及傳遞路徑的有效方法[1-2]。相比經典傳遞路徑分析(classic transfer path analysis,CTPA)，工況傳遞路徑分析僅需要不同工況下目標點與指示點的響應數據，不需要拆分系統及測試系統頻率響應函數與工況載荷力，從而能夠節省實驗時間，實驗效率較高[3-4]。廣泛應用于汽車[5]、高速列車[6-7]及船艦[8]等工程領域。

工況傳遞路徑分析基于傳遞率函數展開實驗，傳遞率定義為運行工況下目標點響應與指示點響應之間的比值[9]。但在實際工程應用中，指示點響應矩陣通常是病態的[10]，因此工況傳遞路徑分析估計傳遞率函數矩陣的過程是一個病態的反問題。Tikhonov正則化是處理反問題的有效方法，通過引入正則化矩陣L和正則化參數[11]，可以提高反問題解的準確度。成瑋等[12]將Tikhonov正則化引入工況傳遞路徑分析中，仿真與實驗結果均表明，相比傳統奇異值分解(singular value decomposition，SVD) 法，Tikhonov正則化法所獲取的各路徑貢獻量精度更高，誤差更小。Li等[13]提出了一種基于條件數準則的多參數Tikhonov正則化方法來估計傳遞率函數。實驗結果表明多參數Tikhonov正則化法有效提升了工況傳遞路徑分析的精度。但在估計傳遞率函數矩陣過程中，正則化矩陣為單位矩陣(即：L=I)，此時稱為標準Tikhonov正則化。標準Tikhonov正則化經過奇異值分解得到的奇異向量振蕩較嚴重，構成的正則化解準確度較低[14]，會影響各路徑貢獻量的計算精度。而正則化矩陣可以約束正則化項，并且正則化矩陣可以控制反問題解的基向量的選擇，因此正則化矩陣可以選擇非單位矩陣[15-16]，此時稱為廣義Tikhonov正則化。采用一階偏導矩陣作為正則化矩陣時，結合廣義奇異值分解，得到的廣義奇異向量振蕩幅度較小，因此構成的正則化解準確度更高。Beck等[17]將廣義Tikhonov正則化引入圖像去模糊中，重構的圖像優于標準Tikhonov正則化結果。Gauthier等[18]利用廣義Tikhonov正則化進行波束形成聲源識別，重構的聲源更加清晰，更加接近原始聲場。因此，廣義Tikhonov正則化是處理反問題更優的選擇，但在工況傳遞路徑分析中應用較少。

為提高工況傳遞路徑分析的準確度，將廣義Tikhonov正則化應用于工況傳遞路徑分析中。將一階偏導矩陣作為正則化矩陣，以廣義奇異值分解得到的廣義奇異向量作為解的基向量，并采用L曲線法選擇正則化參數，分析得到各路徑的貢獻量。最后，在集中質量塊模型上進行工況傳遞路徑分析仿真及在一鋁板上展開工況傳遞路徑分析實驗，驗證廣義Tikhonov正則化工況傳遞路徑分析方法的有效性。

1 工況傳遞路徑分析

假設一系統為線性時不變系統，根據工況傳遞路徑分析理論，指示點響應矩陣X與目標點響應矩陣Y之間的關系可表示為

Y=XT

(1)

式中，T為傳遞率函數矩陣。式(1)展開成矩陣形式

(2)

式中：r為目標點個數；n為指示點個數；m為工況數。為了保證指示點響應矩陣X可逆，要求工況數大于等于指示點數，即m≥n。

1.1 奇異值分解

工況傳遞路徑分析，如式(1)，在估計傳遞率函數矩陣T時，由于指示點響應矩陣X通常是病態的，因此式(1)可看作是一個病態的反問題。奇異值分解常用在反問題求解中。對指示點響應矩陣X進行奇異值分解，有

(3)

式中：U和V分別為左奇異向量ui和右奇異向量vi構成的酉矩陣;VH為V的共軛轉置矩陣；Φ為所有奇異值構成的對角矩陣，Φ=diag(φ1,φ2,…,φn)，且有φ1≥φ2≥…≥φn>0，即所有奇異值按降序排列。

于是通過指示點與目標點響應矩陣得到的傳遞率函數矩陣可表示為

(4)

通過傳遞率函數矩陣及指示點響應矩陣，即可得到每種工況下每條路徑的貢獻量，例如工況1下，各路徑對目標點1的貢獻量為

(5)

由式(4)可知，在求解傳遞率函數矩陣過程中，當目標點響應Y在測量過程中被噪聲ΔY干擾時，較小的奇異值會放大噪聲的影響。最大的奇異值與最小奇異值之比φ1/φn定義為矩陣的條件數，反映矩陣的病態程度。當矩陣條件數越大(矩陣病態越嚴重)，TSVD受誤差影響越嚴重。且根據Hansen和Christensen-Dalsgaard等的研究，隨著i的增大，奇異向量ui和vi振蕩越嚴重，因此TSVD的準確度較低，同時影響每條路徑貢獻量的準確度。為提高其準確度，常用Tikhonov正則化來改善反問題的病態性。

1.2 標準Tikhonov正則化

Tikhonov正則化在最小二乘法的基礎上，通過引入正則化項，并通過Lagrange方程將反問題轉換為無約束最優化問題，從而求解。其目標函數為

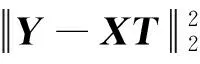
(6)

式中:λ為正則化參數，可通過L曲線選取[19-20]；L為正則化矩陣，通常L=I，即標準Tikhonov正則化。

則標準Tikhonov正則化的解TSTik可表達為

TSTik=(XHX+λ2I)-1XHY

(7)

結合式(4)可得

(8)

式中:ui,vi,φi意義與1.1節中一致，分別為指示點響應矩陣X的奇異向量和奇異值;fi為過濾因子

(9)

用TSTik替換式(5)中TSVD，即可得到每條路徑的貢獻量。

對于較大奇異值，fi趨近1；而對于較小奇異值，fi<1。因此，較小奇異值的影響可通過fi得到改善。

TSTik通過標準Tikhonov正則化引入了過濾因子fi，其準確度相比TSVD有一定程度的改善，但其仍由指示點響應矩陣X的奇異向量構成，仍然會受奇異向量ui和vi較大振蕩的影響。且根據Hansen的研究，雖然奇異向量ui和vi分別為指示點響應矩陣X的列空間和行空間的最佳基向量，但是vi不一定是期望正則化解的最佳基向量。因此，有必要引入非單位矩陣作為正則化矩陣來控制正則化解的基向量選擇，進一步提高傳遞率函數矩陣的準確度。

1.3 廣義Tikhonov正則化

式(6)中，當L≠I時，則稱為廣義Tikhonov正則化。而正則化矩陣L可選擇一階偏導矩陣L1

此時，廣義正則化問題可用矩陣對(X，L)的廣義奇異值分解(generalized singular value decomposition，GSVD)來分析

(10)

γi=ci/si

(11)

最后可得廣義Tikhonov正則化解TGTik

(12)

(13)

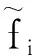
2 仿真分析

為了驗證廣義Tikhonov正則化在工況傳遞路徑分析中的有效性，在九自由度集中質量塊模型[21]上開展工況傳遞路徑分析，如圖1所示。

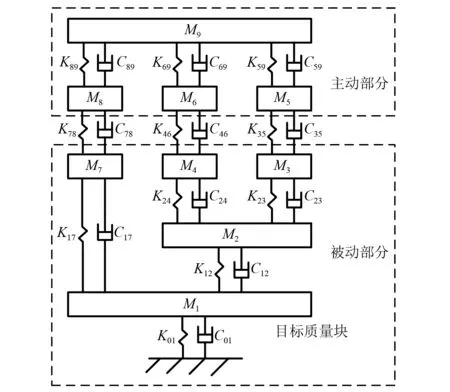
圖1 九自由度模型Fig.1 Nine degrees of freedom model

該模型共包含9個質量塊，各質量塊之間通過彈簧和阻尼單元連接，各質量、剛度與阻尼參數如表1所示。僅考慮各質量塊的平動自由度，忽略轉動自由度。

表1 質量、剛度和阻尼參數Tab.1 The parameters of mass, stiffness and damping

若將被動部分的質量塊M1當作目標點，則主動部分的振動可通過3條路徑傳遞至M1，即路徑35，路徑46和路徑78。用F=10 N(如圖2)分別激勵質量塊M9，M5，M6和M8形成4組工況用來估計工況傳遞路徑分析的傳遞率函數矩陣，分別記為工況一、工況二、工況三和工況四，保證工況數大于路徑數。

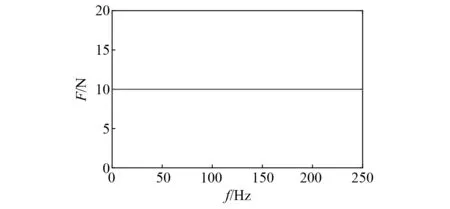
圖2 仿真激勵載荷Fig.2 The load for simulation

2.1 經典傳遞路徑分析

經典傳遞路徑分析雖然耗時長，工作量大，但其準確度較高，因此將經典傳遞路徑分析所得的各路徑貢獻量當作準確值[22]，來驗證廣義Tikhonov正則化在工況傳遞路徑分析中的有效性。

經典傳遞路徑分析第一步需要將系統拆分，如圖3所示，然后獲取被動部分的頻響函數H13，H14和H17。

圖3 拆分模型Fig.3 Split model

經典傳遞路徑分析第二步是獲取質量塊M3，M4和M7受到的工況力(僅考慮工況一)。對于該九自由度模型，可采用懸置剛度法獲取工況力

(14)

式中,(x3,x5,x4,x6,x7,x8)為工況一下的各質量塊位移響應。

最后，通過工況力和對應的頻響函數，即可得到工況一下各路徑的貢獻量(如圖4～圖7所示)。

(15)

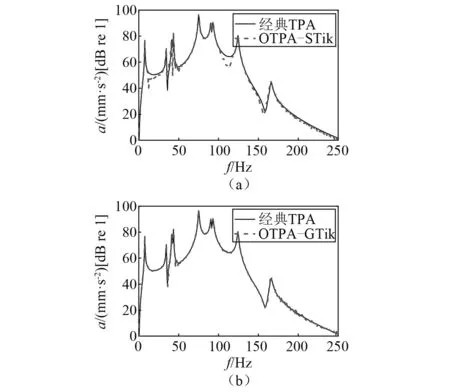
圖4 目標點總響應Fig.4 The total response of the target point

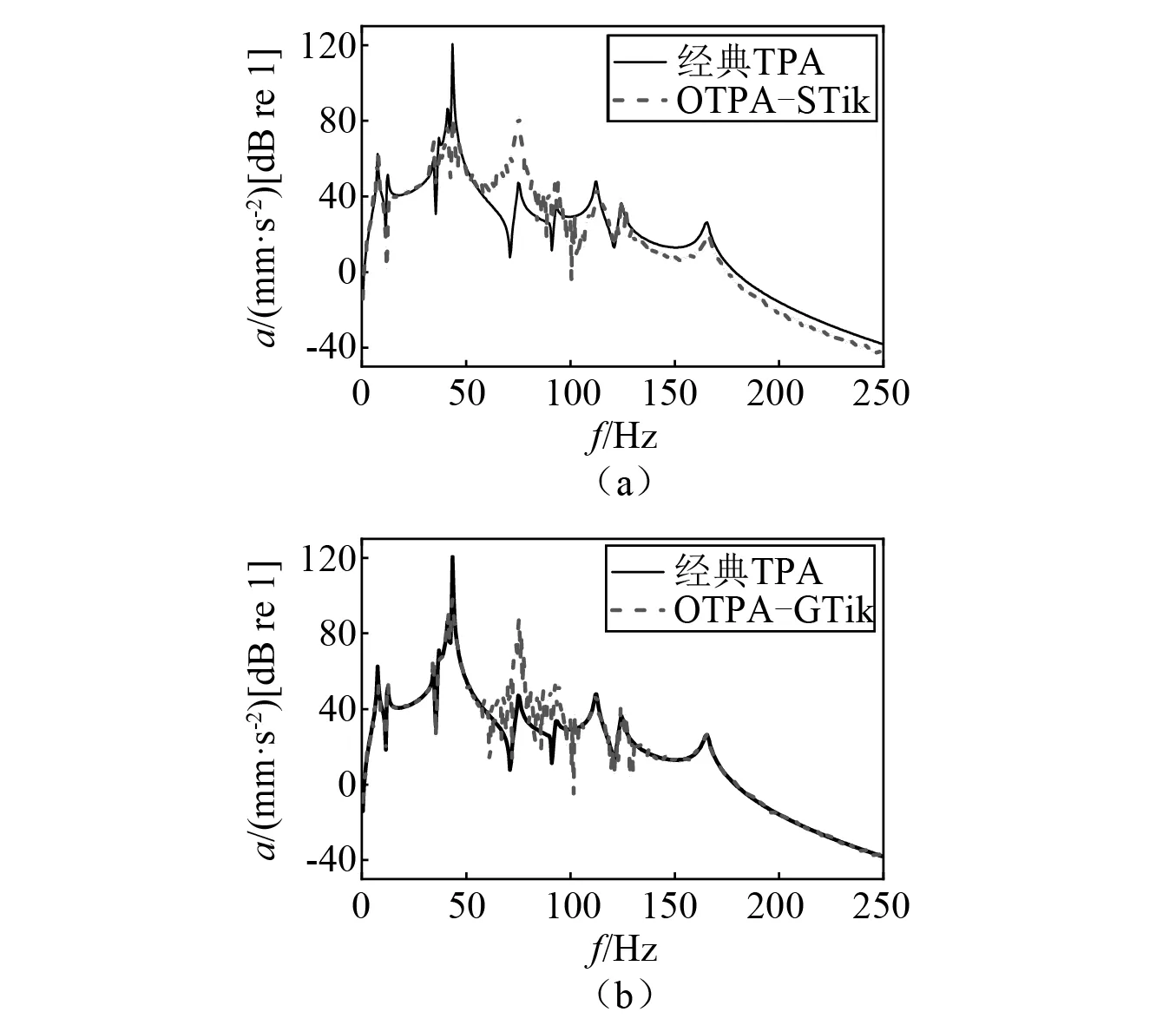
圖5 路徑35Fig.5 The contribution of path 35

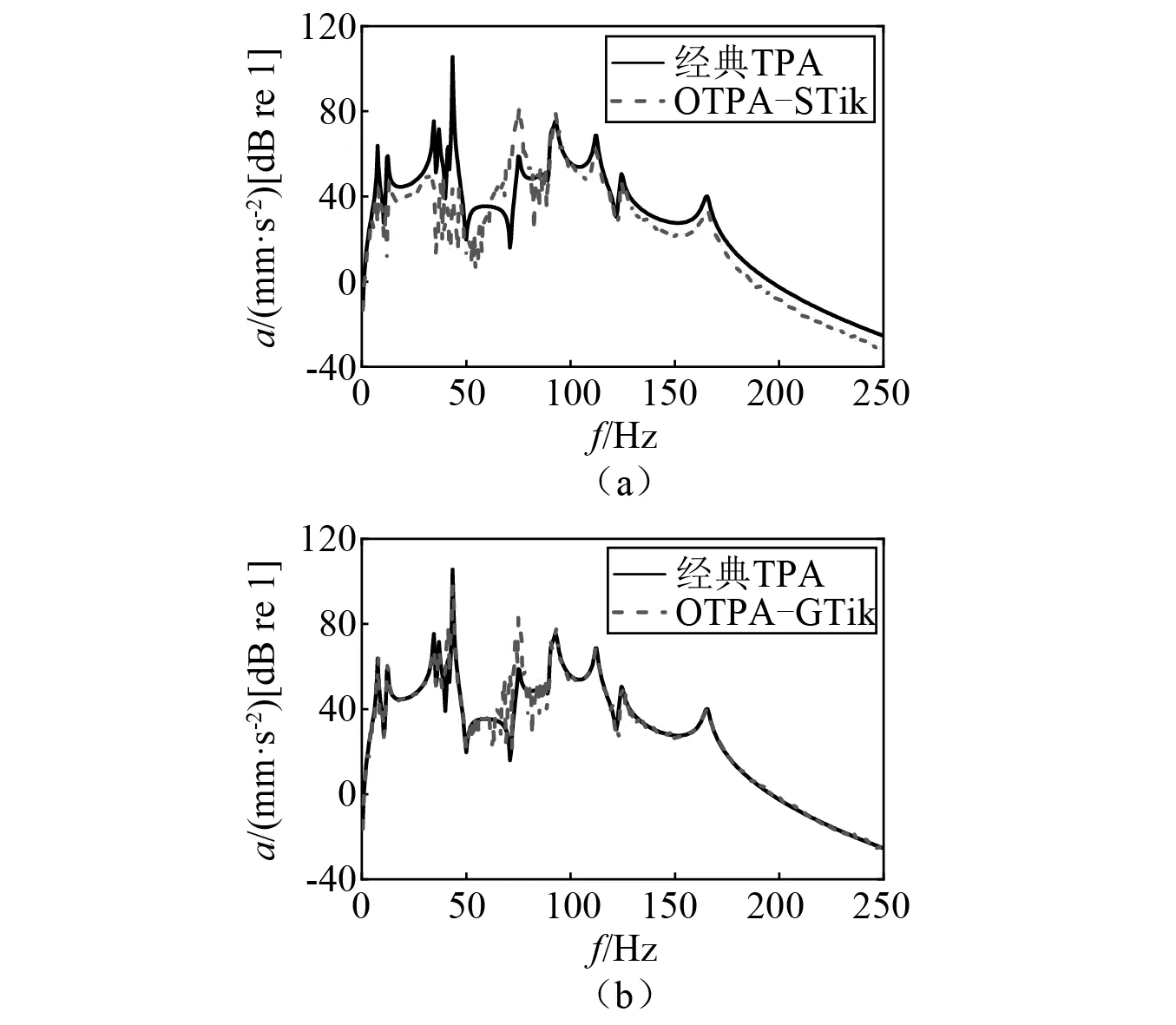
圖6 路徑46Fig.6 The contribution of path 46

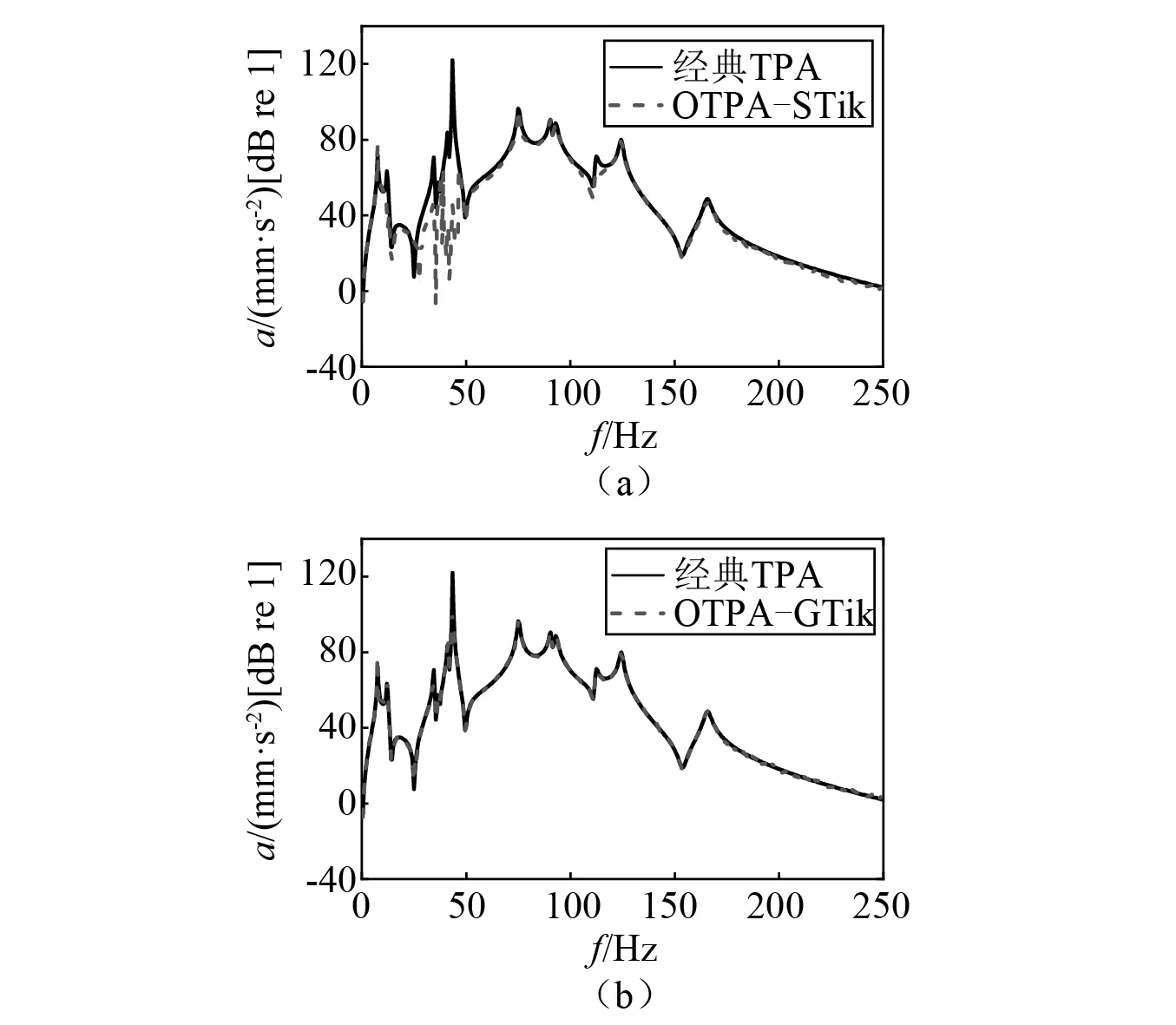
圖7 路徑78Fig.7 The contribution of path 78

2.2 工況傳遞路徑分析

2.2.1 耦 合

在工況傳遞路徑分析中，某個指示點的信號應僅為相應源的響應信號。然而，每種工況下，所有源同時工作，因此每個指示點的信號均耦合有其他源的信息。耦合會影響工況傳遞路徑的貢獻量辨識，若以含有耦合的信號進行工況傳遞路徑分析，準確度較低。在存在耦合的情況下

(16)

為消除耦合的影響，可在主、被動部分上分別布置一個指示點，然后以兩個指示點的響應差進行工況傳遞路徑分析，即指示點響應矩陣取

X=[x3-x5x4-x6x7-x8]

2.2.2 工況傳遞路徑分析

在實際測量過程中，測量數據不可避免會受到噪聲的干擾，因此假設仿真所得的目標點響應矩陣Y和指示點響應矩陣X受隨機噪聲的影響，噪聲服從高斯分布

(17)

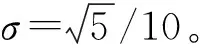
結合4組工況數據，分別運用標準Tikhonov正則化法與廣義Tikhonov正則化法估計目標點與指示點之間的傳遞率函數矩陣。得到傳遞率矩陣后，根據式(5)計算工況一的各路徑貢獻量，并與2.1節的經典傳遞路徑分析各路經貢獻量進行對比，見圖4～圖7。

由圖4可知，廣義Tikhonov正則化法合成的工況傳遞路徑分析總響應與經典傳遞路徑分析總響應吻合很好，而標準Tikhonov正則化法合成的工況傳遞路徑分析總響應在某些頻段稍有偏差。對于路徑35，在60～80 Hz處，兩種工況傳遞路徑方法得到的貢獻量均有偏差，而在其他頻率段，廣義Tikhonov正則化法比標準Tikhonov正則化法準確度高。對于路徑46和路徑78，廣義Tikhonov正則化法得到的貢獻量在整個分析頻率段與經典傳遞路徑分析的貢獻量吻合均較好，而標準Tikhonov正則化法在分析頻段內誤差較大。由此可知，當采用廣義Tikhonov正則化法來估計傳遞率函數矩陣，最后獲取的路徑貢獻量準確度更高，驗證了廣義Tikhonov正則化法在工況傳遞路徑分析中的有效性。

為量化兩種工況傳遞路徑分析法獲取的貢獻量與CTPA結果的匹配程度，引入FRAC(frequency response assurance criteria)值CFRA[23]

(18)

式中：f1與f2為分析的頻段上下限；YOTPA(f)為工況傳遞路徑分析獲得的貢獻量；YTPA(f)為經典傳遞路徑分析獲得的貢獻量；“*”為復共軛。FRAC值介于0～1，1為兩個頻域數據完全匹配。

圖8是兩種工況傳遞路徑分析法的FRAC值。由圖8可知，廣義Tikhonov正則化法的FRAC值均大于標準Tikhonov正則化法的FRAC值，也表明廣義Tikhonov正則化法獲取的路徑貢獻量準確度更高。

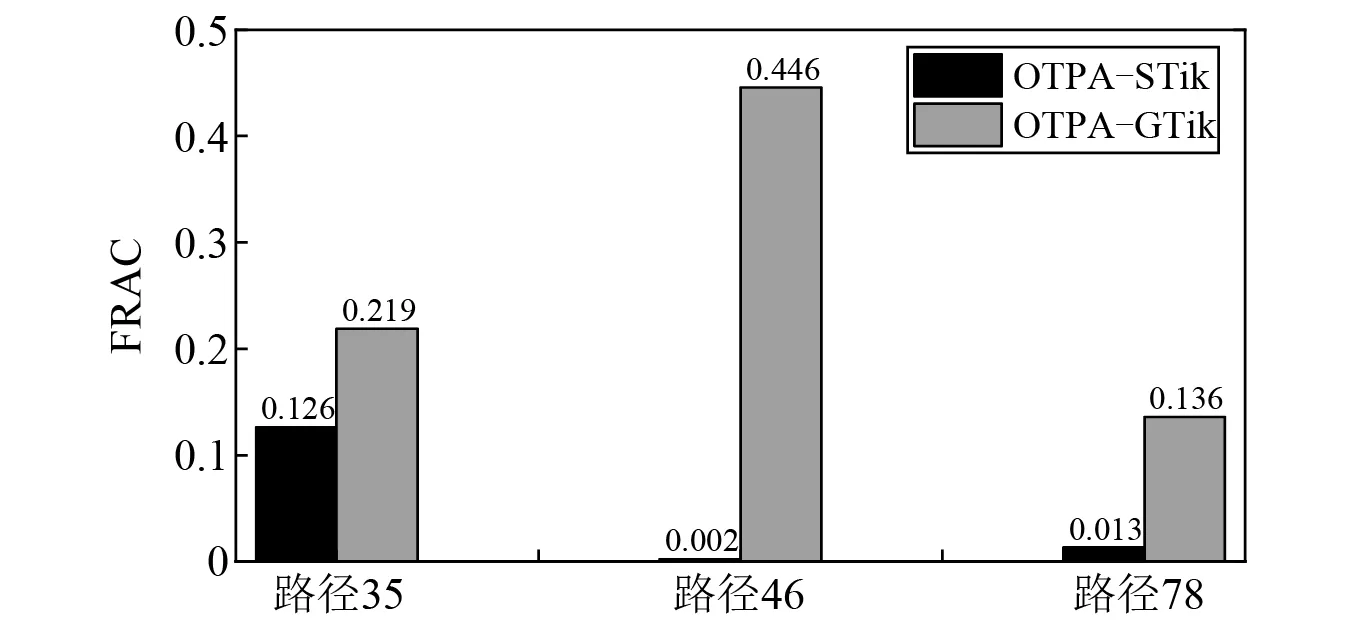
圖8 仿真FRAC值Fig.8 The FRAC value of simulation

3 實驗驗證

為了進一步對比標準Tikhonov正則化法和廣義Tikhonov正則化法在工況傳遞路徑分析中的效果，在一鋁板上進行工況傳遞路徑分析實驗，如圖9所示。鋁板一端固定在支架上。鋁板長×寬×厚為800 mm×400 mm×5 mm，密度為2 700 kg/m3，泊松比為0.31，彈性模量為71 000 MPa。

圖9 實驗布置圖Fig.9 The setup for experiment

激勵源為兩個激振器，記為源a和源b。通過改變激勵類型，產生4組垂直于板面的激勵力(即4組工況，如表2所示)，并分別用兩個力傳感器記錄激勵力的大小。對每個激勵源布置一個指示點(指示點1和指示點2)，指示點應盡量靠近激勵源；選擇點Y為目標點，用加速度計測試指示點與目標點垂直于板面的振動加速度。

表2 實驗工況Tab.2 The experimental operations

3.1 經典傳遞路徑分析

仍以經典傳遞路徑分析獲取的貢獻量為準確值，因此首先進行經典傳遞路徑分析。經典傳遞路徑分析第一步測試源a和源b到目標點Y的頻率響應函數Hya和Hyb。第二步，以力傳感器的輸出值為工況力，即直接測量法獲取激勵源的工況力。頻響函數Hya和Hyb如圖10所示。源a和源b的工況力(工況一)如圖11所示。

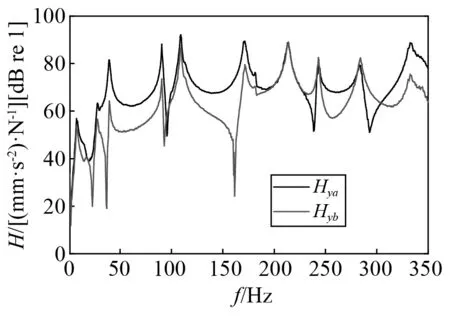
圖10 頻響函數Hya和HybFig.10 FRF Hya and Hyb

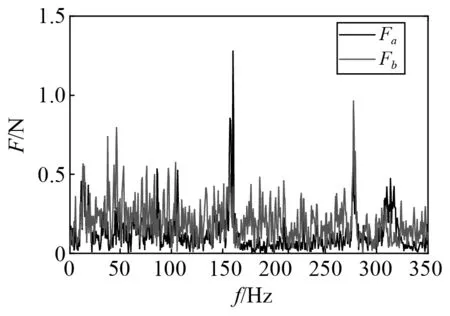
圖11 工況力Fa和FbFig.11 The operational load Fa and Fb

最后通過已獲取的頻率響應函數和工況力，即可得到兩條路徑的貢獻量。兩條路徑貢獻量的總和即為目標點的總響應，并與實際所測目標點響應對比驗證經典傳遞路徑分析的正確性，如圖12所示。由圖12可知，在整個分析頻段內，合成的總響應與目標點實測響應吻合較好，表明經典傳遞路徑分析結果可信。

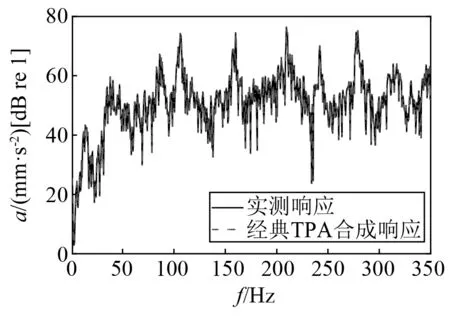
圖12 目標點Y的實測響應與CTPA合成響應Fig.12 The measured response and synthesized response of target point Y

3.2 工況傳遞路徑分析

3.2.1 耦 合

與仿真一致，指示點信號若耦合有其他源的信息，如圖13所示。耦合同樣會影響實驗工況傳遞路徑結果的準確度。因此在進行工況傳遞路徑分析之前，需要消除耦合的影響。

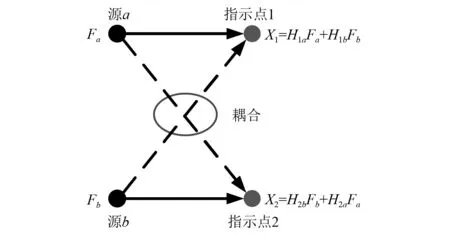
圖13 耦合示意圖Fig.13 The sketch for crosstalk

對于指示點1，其實測響應X1可表示為

X1=H1aFa+H1bFb

(19)

式中:Fa和Fb分別為源a和源b的載荷；H1a和H1b分別為源a和源b到指示點1的頻率響應函數；H1bFb即為X1含有的耦合;Fb通過力傳感器可測得，因此只需測試獲得頻響函數H1b，即可消除X1的耦合部分

(20)

對于指示點2，可采用同樣的方式消除耦合部分。指示點1和指示點2的響應(工況一)消除耦合前后對比，如圖14所示。由圖14可知，指示點信號消除耦合前后，在某些頻段變化較大。因此，若以未消除耦合的信號進行后續工況傳遞路徑分析，勢必降低工況傳遞路徑分析結果的可信度，也說明消除耦合的重要性。

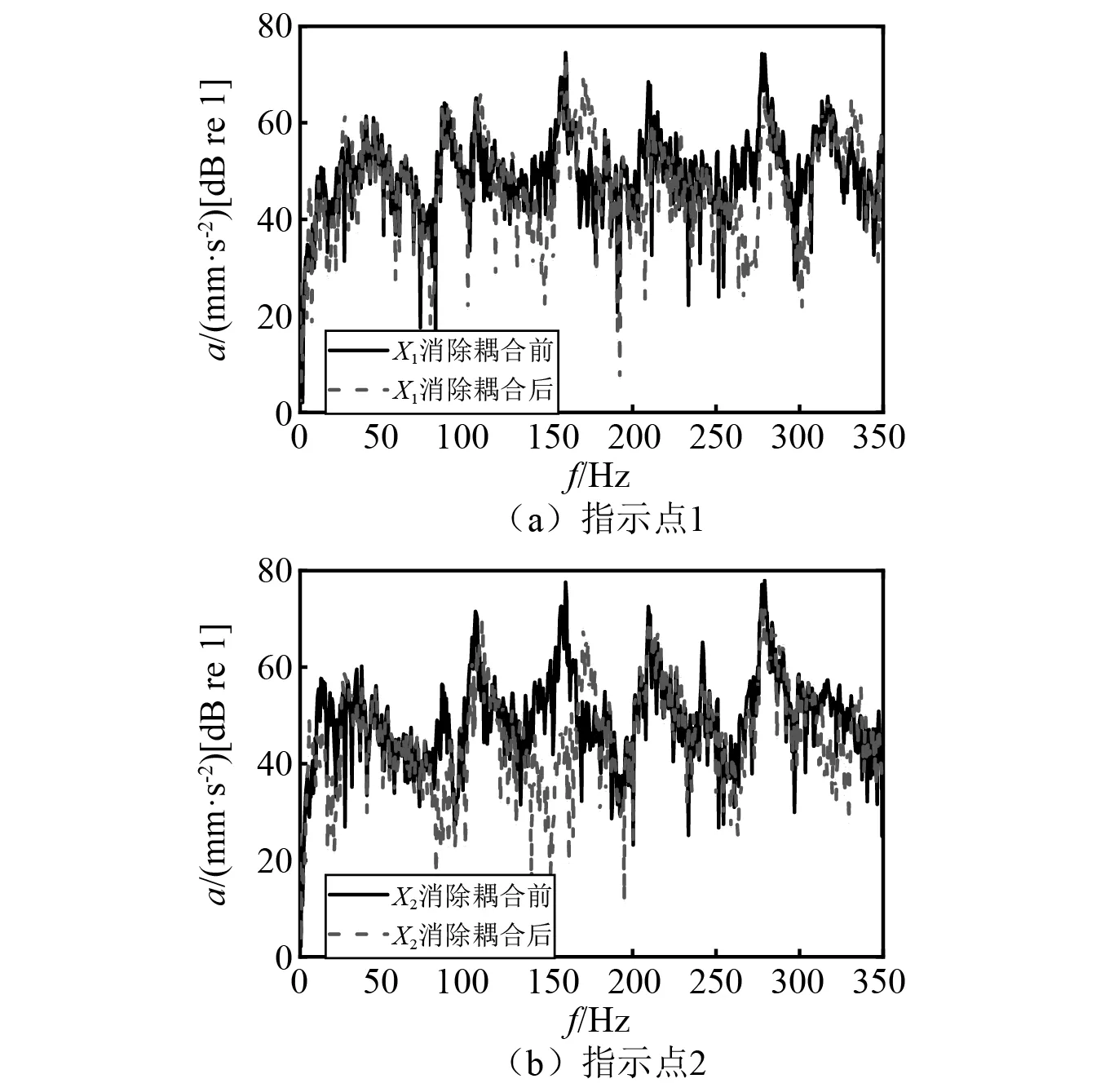
圖14 消除耦合前后對比Fig.14 Comparison before and after eliminating coupling

3.2.2 工況傳遞路徑分析

根據式(20)消除4組工況數據中指示點1和指示點2的耦合部分后，然后分別利用標準Tikhonov正則化法和廣義Tikhonov正則化法估計目標點與指示點之間的傳遞率函數矩陣，最后根據式(5)得到每條路徑的貢獻量。圖15是兩種工況傳遞路徑分析方法合成的目標點總響應曲線圖。圖16與圖17分別是路徑1與路徑2的貢獻量圖。

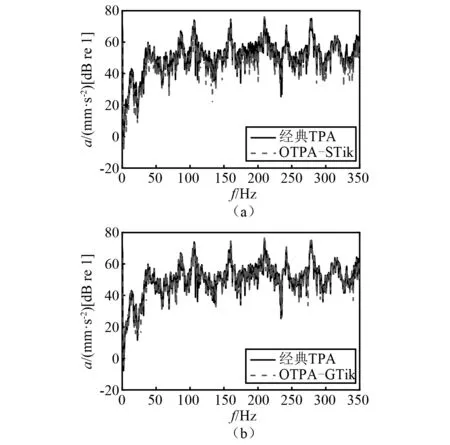
圖15 目標點總響應Fig.15 The total response of target point

圖16 路徑1貢獻量Fig.16 The contribution of path 1

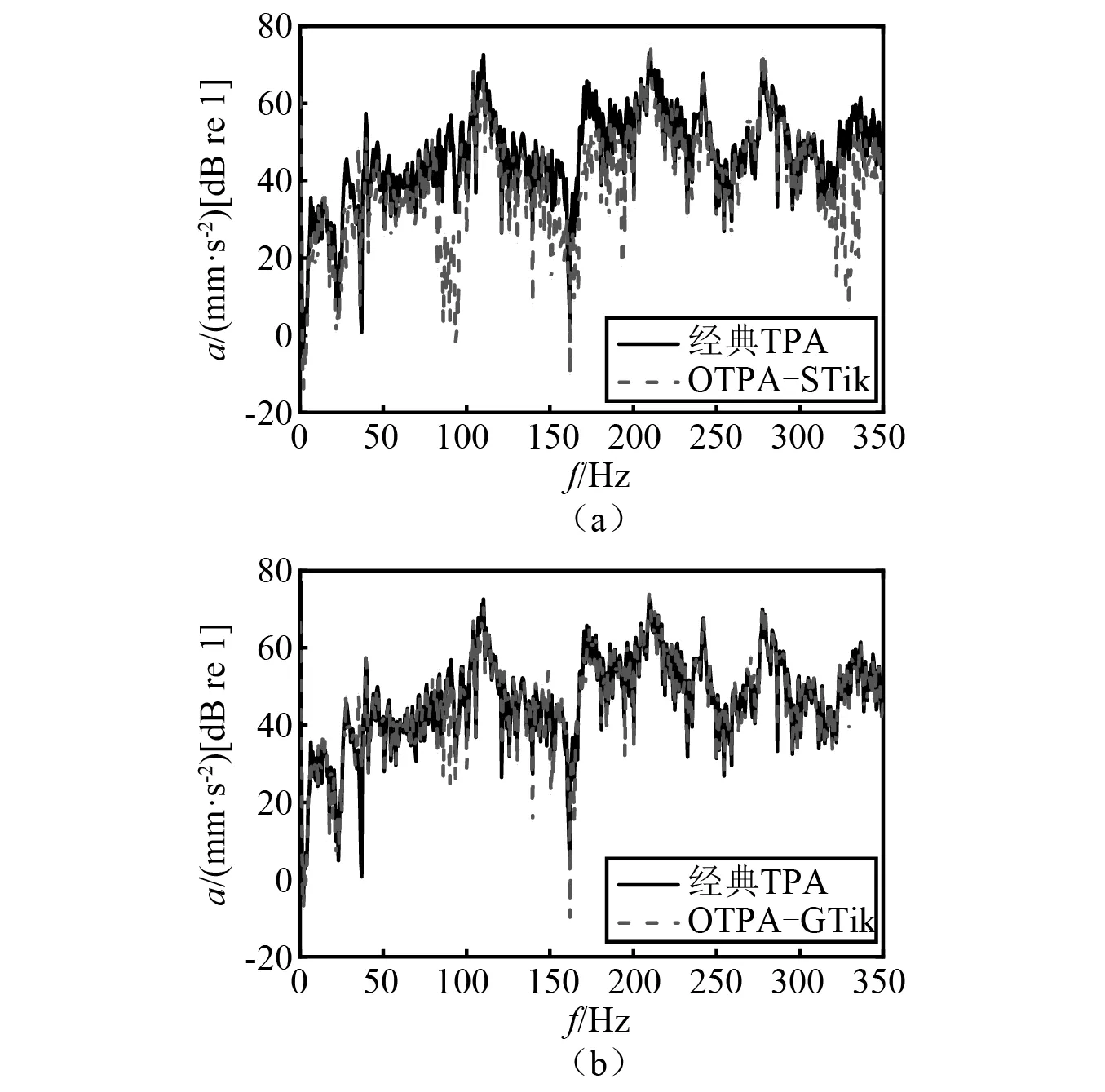
圖17 路徑2貢獻量Fig.17 The contribution of path 2

圖15中，廣義Tikhonov正則化工況傳遞路徑分析法合成的總響應與CTPA結果吻合較好，誤差較小。而標準Tikhonov正則化工況傳遞路徑分析法合成的總響應與CTPA結果有些許偏差，表明標準Tikhonov正則化法在估計傳遞率函數矩陣時，出現了較大的誤差。

從圖16與圖17每條路徑貢獻量結果可知，廣義Tikhonov正則化工況傳遞路徑分析法獲得的每條路徑貢獻量與CTPA結果在整個分析頻段內吻合較好，只在某些頻率有偏差，表明廣義Tikhonov正則化法獲得的傳遞率矩陣準確度較高，識別貢獻量效果較好。而標準Tikhonov正則化工況傳遞路徑分析法獲得的每條路徑貢獻量在整個分析頻段內失真較嚴重，識別貢獻量的準確度較低。

同樣采用FRAC值來對比兩種工況傳遞路徑分析法獲取的貢獻量與CTPA結果的匹配程度。圖18是兩種工況傳遞路徑分析法的FRAC值。由圖18可知，廣義Tikhonov正則化工況傳遞路徑分析法的FRAC值為0.858和0.799，大于標準Tikhonov正則化工況傳遞路徑分析法的FRAC值：0.741和0.635，表明廣義Tikhonov正則化工況傳遞路徑分析的各路徑貢獻量與CTPA結果匹配更好，也說明廣義Tikhonov正則化法用于工況傳遞路徑分析中，能獲得準確度更高的貢獻量，能更準確地識別振動傳遞的主導路徑。

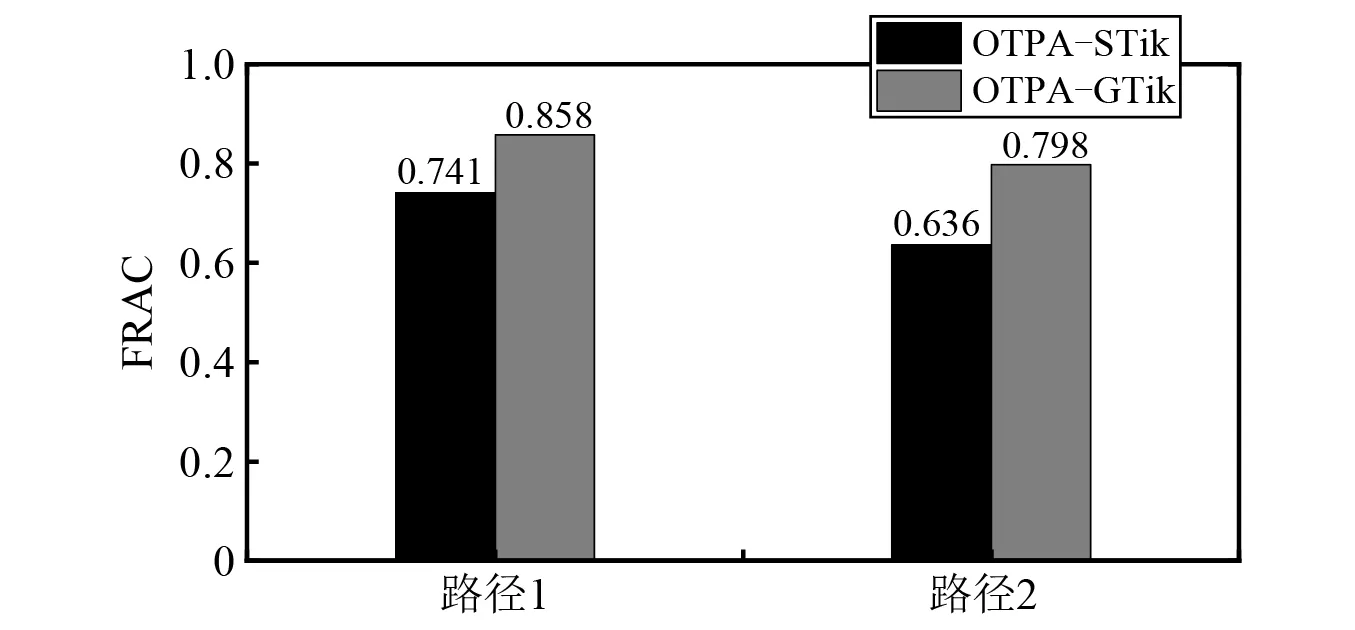
圖18 FRAC值Fig.18 The FRAC value

4 結 論

將以一階偏導矩陣作為正則化矩陣的廣義Tikhonov正則化應用于工況傳遞路徑分析中，利用廣義奇異值分解得到正則化解的基向量和L曲線法選取正則化參數，得到了廣義Tikhonov正則化工況傳遞路徑分析的各路徑貢獻量。最后通過工況傳遞路徑分析仿真與實驗發現，與標準Tikhonov正則化相比，廣義Tikhonov正則化在識別路徑貢獻量方面準確度更高。