從洛書到幻方

張影

什么是幻方

幻方是把從1到n²的自然數(shù)排成的行列的正方形數(shù)表，其每行、每列、每條對角線上的數(shù)之和都相等，這個“和”稱為幻常數(shù)，幻常數(shù)等于n（n²+1）／2?。圖1 是一個三階幻方，即n等于3，n²等于9，幻常數(shù)n（n²+1）／2等于15。

已知三階幻方有8 組，四階幻方有880組（1693年數(shù)據(jù)），五階幻方有275305224 組（1973 年數(shù)據(jù)），更高階幻方的組數(shù)至今還無法確定。

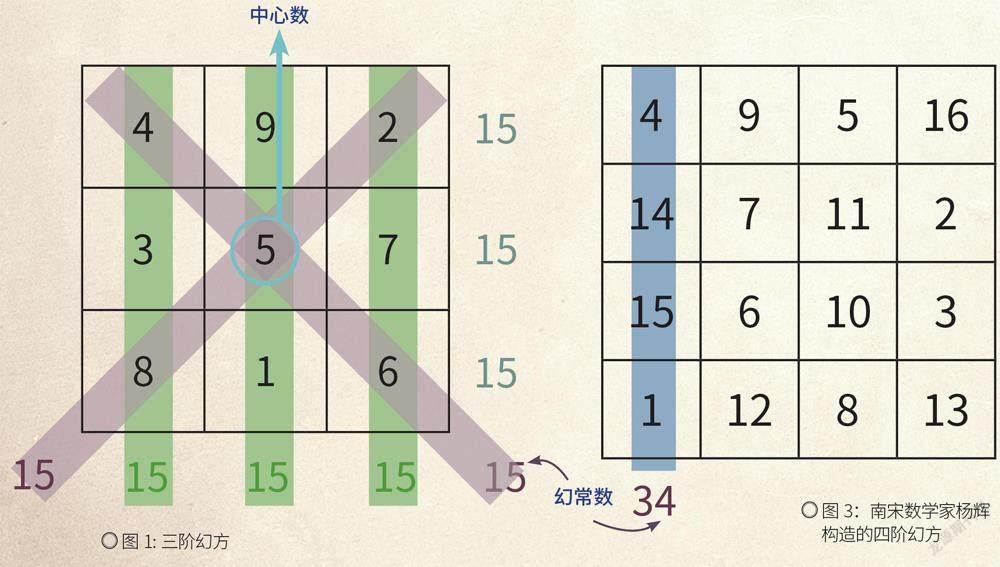
圖2：洛書示意圖

洛書的傳說與縱橫圖

世界上最早的幻方出現(xiàn)在中國。相傳，上古時期，洛河中浮出神龜，背馱洛書，獻給大禹。大禹因此治水成功，劃天下為九州，制定九章大法，治理國家。在長期的歷史發(fā)展中，洛書演化為中國文化的代表符號之一，并被賦予多種解釋。1977 年，阜陽西漢汝陰侯墓（位于安徽省阜陽市）出土的太乙九宮占盤，為洛書提供了考古實物證據(jù)。

圖2 是洛書的示意圖。在數(shù)學上，洛書剛好是三階幻方，按現(xiàn)代書寫順序，正是圖1。

幻方在中國古代被稱為“縱橫圖”。南宋數(shù)學家楊輝的著作《續(xù)古摘奇算法》中記錄了從三階直到九階幻方，連同十階的半幻方（ 不滿足對角線條件），分別稱為四四圖、五五圖、六六圖、衍數(shù)圖、易數(shù)圖、九九圖、百子圖，還給出了三階、四階幻方構造方法的說明。楊輝還研究了幻方的6 種變形。圖3 是楊輝構造的四階幻方。

幻方在現(xiàn)代科學技術中也有廣泛的應用，例如：它的構造原理與飛機的電子回路設置密切相關，研究人員創(chuàng)造的64 階方陣儀可以用于計算機、測量儀、通信交換機及水電、火電、航空等的管理系統(tǒng)。

南宋數(shù)學家楊輝的著作《續(xù)古摘奇算法》