磁電機械天線的阻抗特性分析*
宋凱欣 閔書剛 高俊奇? 張雙捷 毛智能 沈瑩 儲昭強?
1) (哈爾濱工程大學,水聲技術重點實驗室,哈爾濱 150001)
2) (海洋信息獲取與安全工信部重點實驗室(哈爾濱工程大學),哈爾濱 150001)
3) (哈爾濱工程大學水聲工程學院,哈爾濱 150001)
4) (青島哈爾濱工程大學創新發展中心,青島 266071)
機械天線被認為是目前能夠實現甚低頻和超低頻天線小型化的新方案.本文針對1-1 型和2-1 型磁電機械天線的阻抗特性進行系統研究.基于天線振子的阻抗曲線和修正的Butterworth-van Dyke 模型,分別獲得阻抗最小頻率 fm、串聯諧振頻率 fs以及諧振頻率 fr .在此基礎上,本文通過實驗分析了驅動電壓、偏置磁場和機械品質因數(Q 值)對磁電機械天線阻抗特性的影響規律,并結合磁電機械天線的實際工作頻率 fd,獲得了1-1 型和2-1 型磁電機械天線的電阻和電抗分量.實驗結果表明: 無論是1-1 型還是2-1 型磁電機械天線,其電抗分量均小于100 Ω,基本可以看成一個純阻性振子.但是高Q 值的磁電機械天線非線性效應強,且自身阻抗相對較小,難以支持高驅動電壓的加載,輻射能力有限.本文對磁電機械天線的設計優化,特別是在認識其阻抗特性的基礎上進行Q 值選擇,為下一代高輻射性能天線振子的設計提供了重要數據參考.
1 引言
為了實現在損耗介質以及跨域環境中的信息交換,發展高效率、小型化的低頻通信天線是學術界的一個研究熱點和難點[1,2].傳統射頻偶極子天線依賴導體中電子的加速運動產生時變電磁場,其輻射效率與物理尺寸相互制約,無法同時滿足高效、便攜的應用需求[3,4].從突破傳統天線設計思路的角度出發,2018 年美國國防高級研究計劃局(Defense Advanced Research Projects Agency,DARPA)首次公布了機械天線的研究計劃(AMEBA)[2].所謂的機械天線是通過控制電偶極子或者磁偶極子的機械運動,在空間建立時變的電場或磁場來傳輸信息.在4 種典型機械天線的設計方法中[5],宏觀上旋轉駐極體或者永磁體,受限于驅動電機,存在信息加載困難的突出問題.而在微觀上動態調制材料中的電/磁偶極子,基于降低的機械能密度,更易提高天線的輻射效率和信息帶寬[3,5].其中,基于磁電耦合效應的偶極振蕩式機械天線綜合了壓電驅動的高效性和偶極調制的可控性,是發展甚低頻通信技術的關鍵基礎[5].目前,以美國為主的多家研究機構在磁電機械天線的基礎理論及原型樣件方面已開展了一些重要的工作[5?20].例如,2017 年美國東北大學Nan 等[15]首次在實驗上報道了基于磁電多鐵異質結FeGaB/AlN 的NEMS機械天線,解決了傳統天線小型化的設計難題.2019 年,弗吉尼亞理工學院的Xu 等[10]證實: 基于2-1 型磁電復合材料的機械天線與同等尺寸下的線圈發射天線相比,輻射效率提高了近104倍.最近美國東北大學孫年詳教授課題組[21]進一步利用2-1 型磁電復合材料,搭建了甚低頻磁場通信系統,在400 mW 的功耗下,實現了120 m 的發信距離和100 Hz 的調制帶寬.此外,Schneider 等[16]提出的應力耦合型PZT/FeGa 多鐵天線在極低頻(10 Hz)400 V/mm 的驅動電場下有望在1 km 遠處,產生近1 fT 的交流磁場.理論方面,美國加州大學洛杉磯分校的Luong 和Wang[11]基于LLG (Landau-Lifshitz-Gilbert)方程和磁性材料中有效場的來源,定量分析了磁電機械天線中磁彈耦合過程的影響因素.北京大學的儲昭強等[22,23]基于軟磁材料中的Delta-E 效應和磁電諧振器中的非線性動力學模型,研究了磁電機械天線在高場諧振驅動下的雙穩態非線性響應行為,也為進一步優化機械天線的結構設計,提高其功率容量和信息帶寬提供了物理基礎.
機械天線相較于傳統天線的優勢,學術界一般的觀點在于: 1)為了提高輻射效率,傳統天線的口徑大小應與發射電磁波的波長相比擬.但是在同一介質中由于聲速遠小于光速,機械天線基于聲波驅動可以突破傳統低頻天線體積龐大的限制;2) 磁電機械天線工作在聲學諧振模態,基本沒有歐姆損耗,也無需饋電的阻抗匹配網絡,具有進一步增強的輻射效率[1,3,5].現有的研究主要是通過參考同等尺寸下的環形天線,驗證了磁電機械天線中增強的輻射效率,但是基本沒有涉及機械天線的饋電問題,對其阻抗特性也需更加系統和深入地分析.
本文以1-1 型(Metglas/PMN-PZT/Metglas)和2-1 型(Metglas/PZT/Metglas)磁電諧振器為研究對象,實驗總結了應變耦合型磁電機械天線的阻抗特性,并揭示了機械品質因數(Q值)對天線設計的關鍵作用.首先,通過實驗觀察兩種天線振子的阻抗曲線,闡明驅動電壓和偏置磁場對磁電機械天線阻抗特性的影響規律.然后基于修正的Butterworth-van Dyke (modified Butterworth-van Dyke,MBVD)模型,提取磁電機械天線的3 種特征頻率(阻抗最小頻率fm、系統諧振頻率fr以及MBVD 模型中的串聯諧振頻率fs),進一步對比了不同Q值磁電機械天線的阻抗特征.研究發現: 2-1型低Q值天線振子不具有純阻性特點,其逆磁電耦合最強的頻率點不是諧振頻率而是串聯諧振頻率.而對于高Q值的磁電機械天線,三種諧振頻率基本一致,但是均偏離其實際工作頻率.此外,實驗測得1-1 型磁電機械天線的阻抗實部約為200 Ω,難以支持高電壓加載,不滿足磁電機械天線在電場驅動下歐姆損耗小的基本假設.而2-1 型磁電機械天線的阻抗實部則高達6000 Ω,導致其耦合能力較弱,但一定程度上可以通過增大驅動電壓來彌補,實測的磁場輻射能力強于高Q值的1-1 型天線振子.但是兩種天線的電抗分量均小于100 Ω,因此都不需要大的阻抗匹配網絡進行調諧.
2 樣品性能
圖1(a)和圖1(b)分別給出了1-1 型和2-1 型磁電機械天線的結構示意圖和實物照片.有關1-1型和2-1 型磁電復合材料的制備與性能信息,可以參考早期的文獻[24,25].兩種結構均使用非晶軟磁合金Metglas 作為壓磁相,所采用的壓電材料則分別為[011]切向厚度方向極化的單晶纖維PMNPZT (Pb(Mg2/3-Nb1/3)O3-Pb(Zr,Ti)O3)和叉指極化的宏觀陶瓷纖維PZT(Pb(Zr,Ti)O3).兩相材料通過環氧樹脂(West System,105/206)進行復合.這兩種振子分別工作于L-T 模式和L-L 模式,具有很好的代表性.圖1(c)和圖1(d)對比了1-1 型和2-1 型磁電諧振器的正/逆磁電耦合系數和對應的機械品質因數(Q值).正/逆磁電系數用來衡量磁電機械天線磁-電耦合能力的強弱.逆磁電系數的測量,實驗中通過法拉第電磁感應定律,將接收線圈的感應電壓轉換為磁通密度值Br,再根據公式計算出振子軟磁材料中磁感應強度的調制幅度 ?Bmat,其中V為軟磁材料體積,r為接收線圈與磁電機械天線之間的距離,β為輻射電磁場的波數,當接收線圈與磁電機械天線在同一矢徑上時θ為0°[16].已有研究指出: 在磁電諧振器的諧振頻率處發生的是逆磁電效應的共振增強現象,而在反諧振頻率處產生的是正磁電效應的共振增強[26].從圖1(c)和圖1(d)可知對于1-1 型磁電諧振器,測試得到的正/逆磁電效應分別為6000 V/(cm·Oe)和68 (Oe·cm)/V (1 Oe=103/(4π) A/m),而2-1 型磁電諧振器只有2250 V/(cm·Oe)和23 (Oe·cm)/V.本文旨在分析Q值對磁電機械天線的阻抗特性和振子輻射性能的影響規律.聚焦到逆磁電耦合系數,計算得出兩種樣品的Q值分別為189 和113,具有很好的代表性.
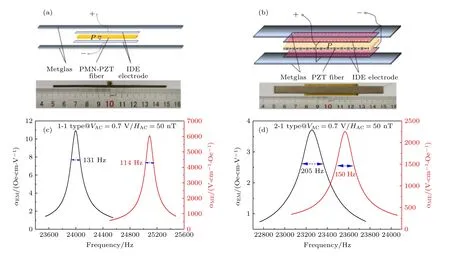
圖1 (a) 1-1 型和(b) 2-1 型磁電機械天線結構示意圖及實物圖;(c) 1-1 型和(d) 2-1 型磁電機械天線的正、逆磁電系數的頻響曲線;對于正磁電系數的測量,激勵磁場為50 nT;對于逆磁電系數的測量,驅動電壓為0.7 VFig.1.Schematic diagram and the snapshot of 1-1 type (a) of and 2-1 type (b) of magnetoelectric antenna;(c),(d) the direct magnetoelectric coefficient αMEand the converse counterpart αEM as a function of driving frequency for 1-1 type (c) of and 2-1 type(d) of magnetoelectric antenna.The driven magnetic field for direct magnetoelectric coefficient measurement and the driven voltage for converse magnetoelectric coefficient measurement is 50 nT and 0.7 V,respectively.
3 結果和討論
圖2 給出了對兩種磁電機械天線阻抗曲線的測試結果,主要研究了磁電機械天線驅動電壓和偏置磁場對阻抗特性的影響.在圖2(a)和圖2(b)中固定直流偏置磁場,將加載在磁電機械天線壓電材料上的驅動電壓從0.1 V 增至0.9 V.阻抗曲線通過阻抗分析儀(E4990A,Keysight,USA)掃頻獲得.從圖2(a)可知,隨著驅動電壓的增大,1-1 型磁電機械天線的諧振峰向左偏移,即系統發生了彈簧軟化行為(是指對于一個非線性的振動系統,其等效剛度隨著振動幅度的增大而下降).而2-1 型磁電機械天線的諧振峰位置則基本不變,系統維持了很好的線性動力學響應.在圖2(c)和圖2(d)中,設置磁電機械天線的激勵電壓為1 V,偏置磁場從2.68 Oe 增至29.48 Oe.這里單獨給出兩種磁電機械天線阻抗的幅頻響應曲線,可以看出逐漸增大1-1型磁電機械天線的直流偏置磁場時,其諧振峰位置先左移后右移,滿足軟磁材料Delta-E 效應[22].而2-1 型磁電機械天線也表現了類似的行為.以上是傳統文獻對磁電諧振器阻抗特性的基本描述.借鑒水聲換能器理論,諧振式磁電器件客觀上有3 個所謂的“諧振頻率”: 第1 種為阻抗最小的頻率點fm,在此頻率點上磁電機械天線整體的阻抗模值最小.第2 種為純阻性頻率點fr,在此頻率點上磁電機械天線的阻抗角為0°,可認為整體為純阻性的狀態.第3 種為磁電機械天線等效電路MBVD模型中的串聯諧振頻率點fs.但是目前對磁電機械天線的研究基本不區分這3 種頻率.下面,本文將通過MBVD 模型[27,28],提取出磁電機械天線的串聯諧振頻率fs,并在不同驅動條件下分析3 種特征頻率的變化規律,以進一步認識其阻抗特性.
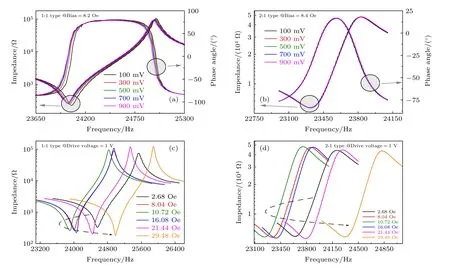
圖2 不同驅動條件下磁電機械天線的阻抗特性 (a),(b) 不同驅動電壓下(a) 1-1 型和(b) 2-1 型磁電機械天線的阻抗、阻抗角頻響曲線;(c),(d) 不同直流偏置磁場下(c) 1-1 型和(d) 2-1 型磁電機械天線的阻抗頻響曲線Fig.2.Impedance characteristics of 1-1 type (a),(c) of and 2-1 type (b),(d) of magnetoelectric antenna under different driven conditions: (a),(b) Different driven voltages with constant bias fields;(c),(d) different bias fields with constant driven voltage.
如圖3 所示,磁電機械天線可以通過等效電路模型進行分析.常見的有Mason 模型、BVD 模型和MBVD 模型等.MBVD 模型可以更準確地體現元器件整體的損耗特性,多用于壓電器件的等效分析.磁電機械天線的典型等效電路MBVD 模型如圖3 所示,其中Lm,Cm,Rm分別為磁電機械天線的等效電感、等效電容和等效電阻,三者構成了動態支路;C0和R0分別是靜態電容與靜態電阻,Rs表示電極損耗.在圖3 所示電路中,fs對應動態支路的串聯諧振在磁電機械天線實際工作時,從輸出磁場的掃頻曲線中提取的諧振頻率,稱為工作頻率fd.
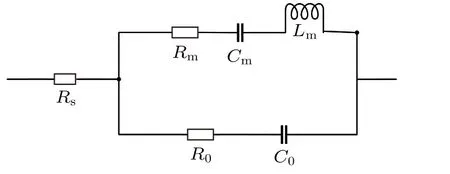
圖3 磁電機械天線的等效電路MBVD 模型Fig.3.Equivalent circuit MBVD model of magnetoelectric antenna.
由圖3 可知: 整個回路的阻抗模值
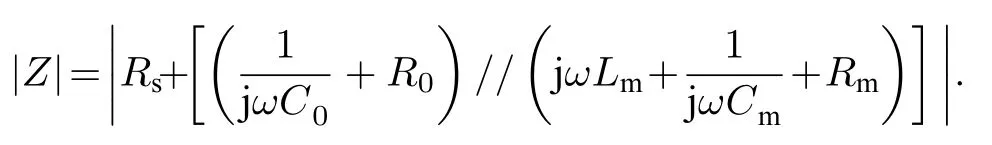
基于實驗測量的阻抗模值曲線和非線性參數擬合可以確定MBVD 模型中的參數值,進而獲取串聯諧振頻率fs.非線性曲線擬合方法較多,常用的有Levenberg-Marquardt 法、Gauss-Newton 法、Gradient descent 法以及Powell 法等,本文擬合中選擇Levenberg-Marquardt 法.Levenberg-Marquardt算法作為非線性優化的標準方法,能提供非線性最小化(局部最小)的數值解,適合對于諧振頻率和非諧振頻率的搜索,并且具有Gauss-Newton 法和Gradient descent 法的優勢,同時又降低了初始值離局部極小值太遠時優化失效的失敗率,即對初值不敏感.擬合結果如圖4 所示.
圖4(a)和圖4(b)中,兩種磁電機械天線的驅動電壓統一為0.5 V,偏置磁場分別固定為8.2 Oe和8.4 Oe.從圖4 可以看到,阻抗曲線的MBVD模型擬合結果和實測結果基本吻合.相應的擬合參數在圖中也有標注(見圖4(a)和圖4(b)中的插圖).通過計算,圖4(c)和圖4(d)分別給出了1-1 型和2-1 型磁電機械天線中3 種諧振頻率(fm,fs,fr)的位置.對于Q值更高的1-1 型機械天線,3 種諧振頻率相差較小fm≈fs≈fr,說明此時磁電機械天線的機械損耗很小.在這種情況下基本可以認為諧振式磁電機械天線工作于純電阻狀態,這對于磁電機械天線的阻抗匹配,即“饋電”的設計是有利的.但是對于Q值較低的2-1 型磁電機械天線,3 種諧振頻率之間的關系則為fm 圖4 (a),(c) 1-1 型和(b),(d) 2-1 型磁電機械天線的實測阻抗曲線及其擬合計算結果.(c),(d)分別標注了對應的3 種特征頻率fm,fs,frFig.4.Measured and the fitted impedance curves for 1-1 type (a),(c) of and the 2-1 type (b),(d) of magnetoelectric antenna.Three kinds of resonance frequencies fm,fs,fr are marked on panel (c) and (d). 以1-1 型和2-1 型兩種不同Q值磁電機械天線中的3 種諧振頻率為觀察對象,圖5 定量分析了驅動電壓和偏置磁場對兩種磁電機械天線的影響規律.從圖5(a)可看到在固定偏置磁場時,1-1 型磁電機械天線在較低的電壓(驅動電壓 ≤ 1 V)驅動下表現了明顯的彈簧軟化行為,頻率的變化說明此時系統存在非線性效應.3 種諧振頻率在不同驅動電壓下也是基本重合(?f <10 Hz).有關磁電諧振器的非線性動力學理論可參考我們過去的研究結果[22,23].而對于2-1 型磁電機械天線,3 種諧振頻率在不同驅動電壓下基本保持不變,說明此時系統基本沒有非線性效應.考慮偏置磁場對3 種諧振頻率的影響,圖5(c)和圖5(d)給出的結果和前文的分析結論一致.只是在較低的磁場偏置(Hbias<10 Oe)下,2-1 型磁電機械天線中的3 種諧振頻率的大小關系出現了異常,其原因不是本文的關注內容,有待將來進一步的研究. 圖5 (a),(c) 1-1 型和(b),(d) 2-1 型磁電機械天線的3 種特征頻率(fm,fs,fr)與驅動電壓(a),(b)和偏置磁場(c),(d)的關系.Fig.5.Three kinds of resonance frequencies fm,fs,fr for 1-1 type (a),(c) of and 2-1 type (b),(d) of magnetoelectric antenna as a function of the driven voltage (a),(b) and the applied bias field (c),(d). 圖6 分析了磁電機械天線的實際工作頻率fd與3 種諧振頻率的關系,并計算了其工作狀態下的阻抗實部與相角.采用文獻[23]中的試驗方法.通過空芯螺線管來接收磁電機械天線在近場(距離30 cm)產生的磁能量.圖6(a)和圖6(b)給出了接收螺線管中感應電流的掃頻結果,其中工作頻率fd對應于掃頻曲線中峰位.圖6(c)和圖6(d)匯總了3 種諧振頻率及工作頻率隨驅動電壓的變化情況.從圖6(c)可以看到,在驅動電壓低于1 V 的情況下,1-1 型磁電機械天線的實際工作頻率偏離其諧振頻率.另外需要注意的是,對于高Q值的磁電機械天線,隨著驅動電壓的增加,其Q值有明顯下降的趨勢(見圖6(c)的右側軸).圖6(c)中,在1 V驅動時,1-1 型機械天線的Q值從225 下降到190.此時其實際工作頻率基本和其串聯諧振頻率相重合.對于低Q值的2-1 型磁電機械天線,可以明顯看到: 其實際工作頻率接近串聯諧振頻率.和1-1型磁電機械天線所不同,2-1 型磁電機械天線的Q值隨著驅動電壓的增大,沒有表現出下降的行為,反而有輕微的上升趨勢.最后圖6(e)和圖6(f)計算了兩種天線的阻抗實部和相角,以反映其電抗和電阻大小.可以看出1-1 型磁電機械天線的阻抗實部只有250 Ω 左右,但是其低場驅動下的相角較大.2-1 型磁電機械天線的阻抗實部大約是6000 Ω,但是其相角小,容抗并不大,大約只有幾十歐姆.因此,無論是1-1 型還是2-1 型機械天線,均不需要大的匹配網絡進行調諧. 圖6 不同驅動電壓下,1-1 型(a)和2-1 型(b)磁電機械天線輻射場強(以接收螺線管中的感應電流為替代測試對象)的掃頻曲線;不同驅動電壓下,1-1 型(c)和2-1 型(d)磁電機械天線的3 種特征頻率與實際工作頻率(對應于接收信號頻響曲線的最高值);不同激勵電壓下1-1 型(e)和2-1 型(f)磁電機械天線實際工作的電阻和相角Fig.6.Induced current in the pick-up coil as a function of the driving frequency under different driving voltages for 1-1 type (a) of and 2-1 type (b) of magnetoelectric antenna;three kinds of resonance frequencies (fm,fs,fr) and the working frequency fd as a function of the driving voltages for 1-1 type (c) of and 2-1 type (d) of magnetoelectric antenna;the resistance component and the phase angle of 1-1 type (e) of and 2-1 type (f) of magnetoelectric antenna under different driving voltage. 圖7 最后對比了1-1 型和2-1 型磁電機械天線磁場輻射能力和功率容量的差異,實驗中磁場接收線圈與磁電機械天線距離30 cm.對于高Q值的1-1 型磁電機械天線,在驅動電壓增至25 V 時,系統表現出了強的混沌現象.輻射的磁場強度在6×10–5—1.9×10–4Oe 之間呈現無規律的跳變,其物理起源是高Q值諧振器在高場諧振驅動下強的非線性特性.而對于2-1 型機械天線,當驅動電壓增至90 V 時,此時系統的輻射能力趨于飽和,最大輻射磁場強度約為5.5×10–4Oe.在進一步降低驅動電壓的過程中,2-1 型磁電機械天線的輻射性能表現了一定的洄滯現象,這可以歸因于軟磁材料中磁疇的不可逆翻轉.不難看出2-1 型磁電機械天線的輻射能力強于1-1 型磁電天線.前者的功率容量受限于系統的飽和問題,而后者則是系統的非線性混沌現象. 圖7 1-1 型和2-1 型磁電機械天線輻射能力對比 (a) 1-1 型磁電機械天線在正向掃場下的輻射磁場大小;(b) 2-1 型磁電機械天線在正反向掃場下的輻射磁場Fig.7.Comparison of the radiation capability of magnetoelectric antennas with different Q values: The received magnetic field from 1-1 type (a) of and 2-1 type (b) of magnetoelectric antenna by electric field sweeping. 本文系統研究了1-1 型和2-1 型磁電機械天線的阻抗特性,重點分析了天線振子機械品質因數對天線設計的重要影響.研究發現: 對于低Q值的磁電機械天線,輻射強度在串聯諧振頻率處具有最大值;對于高Q值的天線振子,本文研究的3 種特征頻率基本重合,但是均偏離其實際工作頻率.另一方面,兩種天線的電抗分量均小于100 Ω,因此都不需要大的阻抗匹配網絡進行調諧.然而高Q值的磁電機械天線振子在串聯諧振頻率處,阻抗實部只有200 Ω 左右,難以支持高電壓加載,而且非線性效應較強,輸出響應容易飽和.低Q值高帶寬機械天線耦合能力弱的不足,一定程度上則可以通過增大驅動電壓來彌補.因此在進行磁電機械天線的結構和饋電設計時,需要對Q值進行平衡,以同時實現強耦合強輻射的應用需求.在本文的基礎上,我們也在進行下一代磁電天線振子的結構設計,期望能夠解決目前甚低頻磁電天線難以走向應用的瓶頸問題.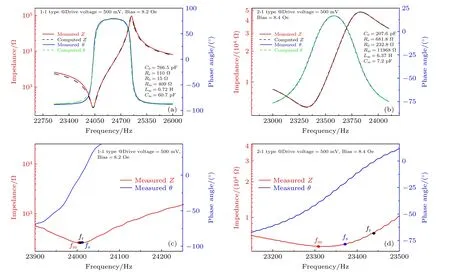
4 結論

