Fe 基合金應力感生不可逆磁各向異性機理*

張建強 秦彥軍 方崢 范曉珍 楊慧雅 鄺富麗 翟耀 苗艷龍 趙梓翔 何佳俊 葉慧群 方允樟?

1) (浙江師范大學物理與電子信息工程學院,金華 321004)

2) (天水師范學院電子信息與電氣工程學院,天水 741001)

3) (浙江師范大學浙江省固態光電器件重點實驗室,金華 321004)

4) (浙江旅游職業學院,杭州 311231)

Fe 基合金因獨特的磁性能和簡單的生產工藝,被視為是重要的“雙綠色”節能材料.本文對Fe73.5Cu1Nb3 Si13.5B9 非晶薄帶進行不同物理時效處理(張應力退火、回火),采用動態應變測量技術,結合縱向驅動巨磁阻抗效應和同步輻射X 射線衍射研究應力感生磁各向異性和晶格各向異性的弛豫動力學,探尋應力感生磁各向異性的物理起源.結果表明: 退火過程薄帶軸向應變在玻璃轉變點以下表現為彈性,在玻璃轉變點以上主要表現為塑性;感生磁各向異性和晶格各向異性表現出不同的弛豫動力學,數值擬合預言前者通過無限次回火歸一化的磁各向異性趨于 κ=0.144 的穩態值,而后者僅通過有限次回火便可弛豫為0;構建納米晶分布各向異性模型,主張應力感生不可逆磁各向異性Kd 是由納米晶分布各向異性 ?δ所致,且滿足 Kd=k?δ 的函數關系.本文認為應力感生磁各向異性起源于納米晶晶格各向異性和分布各向異性的協同作用,對理解應力感生磁各向異性機理具有指導意義.

1 引言

Fe 基軟磁非晶/納米晶合金,因其獨特的磁性能(高磁導率和低矯頑力)及簡單的生產工藝[1?3],被業界視為是重要的“雙綠色”節能材料[4?7].然而,以Fe 基合金為基礎材料制備的非晶/納米晶軟磁器件并未真正體現出材料應用的性能優勢,其中一重要原因是對應力敏感問題的認識尚存爭議.

眾多學者以應力感生磁各向異性(stress-induced magnetic anisotropy,SMA)機理研究為突破口,試圖在理論和技術上致力于應力敏感問題的突破[8?11].基于Néel[12]在二元合金體系中提出原子對有序模型,Hofmann 和Kronmüller[13]指出Fe-Si 原子對的有序化是SMA 的主要原因.Herzer[14]在滯彈性極化模型[15]基礎上提出α-Fe(Si)納米晶殘余內應力與其磁致伸縮的磁彈耦合是SMA 的物理機制.Ohnuma 等[16,17]采用透射X 射線衍射技術研究張應力退火Fe 基合金的微觀結構,發現衍射矢量平行于張應力方向晶面衍射峰往低角度偏移,垂直應力方向往高角度偏移,指出晶格各向異性(lattic plane anisotropy,LPA)是SMA 直接的實驗證據.隨后Ohnuma 等[18]再次發現α-Fe(Si)納米晶的晶格應變是淬滅的彈性應變,指出Fe 基非晶合金晶化形成α-Fe(Si)納米晶鑲嵌于非晶基底的雙相結構是晶格彈性應變能夠得以保留的原因.方允樟等[19?21]采用同步輻射X 射線原位測試技術動態觀測研究退火過程Fe 基合金薄帶微觀結構演變規律,指出LPA 是SMA 的微觀結構起源.迄今為止,多數學者認為磁彈耦合是SMA 的物理機制[3,22?24].然而,磁彈耦合理論卻面臨諸多挑戰,如大磁致伸縮材料中感生小的磁各向異性,相反小磁致伸縮或近零磁致伸縮材料中卻感生了大的磁各向異性[23,25,26].此外,在磁彈耦合模型框架內,晶格彈性應變貢獻的磁各向異性可以通過回火的方式完全消除[13,15,23].近期許校嘉等[27]采用實驗和數值擬合的方法研究了磁各向異性與回火次數的函數關系,指出SMA 不能通過回火的方式完全消除.基于以上實驗結果,有必要重新審視SMA 的物理起源,理由是磁彈耦合模型僅考慮了α-Fe(Si)納米晶的殘余彈性應變,而忽視了雙相結構中非晶基底塑性應變對SMA 的貢獻.

因此,本文借助動態的應變測量技術,研究張應力退火過程合金薄帶軸向宏觀應變的演變規律及退火結束后殘余宏觀應變與外加張應力的函數關系.利用縱向驅動巨磁阻抗(longitudinally driven giant magneto-impedance,LDGMI)效 應和同步輻射X 射線衍射(synchrotron radiation xray diffraction,SRXRD)研究SMA 和LPA 的弛豫動力學.以自由退火Fe 基合金納米晶各向同性分布結構為參考,構建納米晶分布各向異性(nanocrystalline grain distribution anisotropy,NGDA)模型,提出α-Fe(Si)納米晶LPA 和NGDA 的協同作用是SMA 的物理起源.本研究對深入理解SMA機理具有重要的指導意義.

2 實驗與方法

2.1 張應力退火及回火

單輥快淬制備組分為Fe73.5Cu1Nb3Si13.5B9(Fe基)的非晶合金薄帶,取長220 mm、寬1 mm、厚33 μm 的非晶帶,氮氣氛圍沿薄帶軸向施加張應力退火(升溫速率為51 ℃/min,退火時間為30 min,退火溫度為540 ℃,退火張應力分別為0,53,117,170,223,270,341,410 MPa).退火過程中利用Supereyes B011 5MP 500X 數字攝像顯微鏡及Supereyes 軟件,動態檢測合金薄帶軸向宏觀應變的演變規律,其應變按(1)式測量計算:

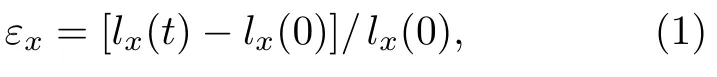
其中,lx(t) 為退火過程某一時刻t合金帶的長度,lx(0)為退火前合金帶的初始長度.文中規定t=∞為退火終了時刻(卸載載荷后時刻),則lx(∞) 為卸載載荷后合金帶的長度,由(1)式可測量合金帶的軸向殘余應變.而橫向殘余應變按(2)式測量計算:

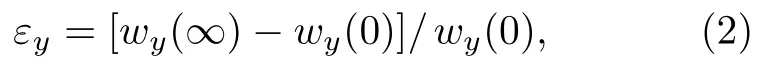
其中,wy(∞)為卸載載荷后合金薄帶的寬度,wy(0)為張應力退火前合金薄帶的初始寬度.此外,在相同退火條件參數下對170 MPa 張應力退火合金薄帶實施多次等溫回火處理,回火次數n分別為0,1,2,3,4,5,15,24,48 和140.

2.2 巨磁阻抗測量

直徑φ=0.1 mm 的銅漆包線繞制內徑 1.5 mm、長10 mm 的驅動線圈,將長度15 mm 的Fe 基合金薄帶插入線圈組成等效阻抗元件,置于直徑?=200 mm 的Helmholtz 線圈所提供的直流勻場區,測量過程使薄帶軸向始終與地磁場保持垂直.在幅值為10 mA 的正弦激勵信號和外加直流磁場下,采用HP4294A 型阻抗分析儀測量張應力退火及回火合金薄帶的LDGMI 效應.利用求半高寬的方法測量橫向磁各向異性場,其測量關系式為

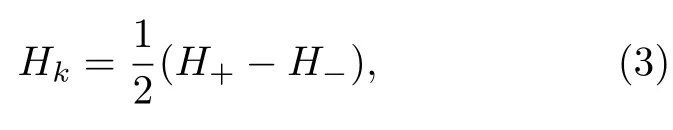
其中,Hk為橫向磁各向異性場,H+和H–分別為LDGMI 曲線最大值一半處所對應的正向和反向外加磁場.由(3)式和可計算合金帶的磁各向異性,其中Js=1.24 T[13]為Fe 基納米晶合金的飽合磁極化強度.

2.3 同步輻射X 射線衍射

采用自行設計并搭建于上海同步輻射光源的專用測試裝置[21],利用BL13W 線站硬X 射線衍射技術拍攝張應力退火及回火Fe 基合金帶的平面衍射圖,其中硬X 射線能量E=30.0 keV,波長λ=0.0414 nm,分辨率為2.5×10–4.隨后利用FIT2D軟件將平面衍射圖轉換為衍射強度I關于2θ角的SRXRD 譜,測量記錄各晶面衍射峰半高寬B和峰位角2θ,以標樣硅的衍射半高寬作為BL13W 線站的儀器展寬,經扣除后再利用布拉格公式和謝樂公式:

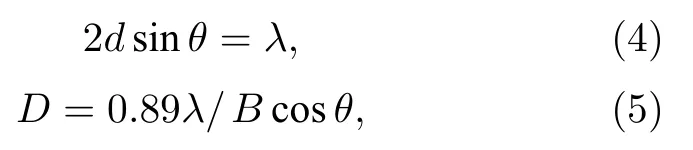
計算晶面間距d和晶粒尺寸D.選自由退火Fe 基納米晶合金SRXRD 譜的(110)峰,利用分峰擬合和Pseudo-Voigt 方法[28,29]按(6)式計算納米晶晶化分數:

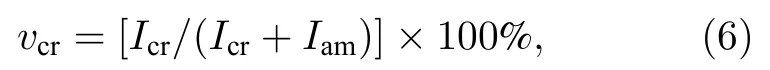
其中,Icr和Iam分別為晶化峰和非晶峰的積分強度.

3 結果與討論

3.1 宏觀應變及巨磁阻抗效應

文中規定Fe 基合金薄帶長度方向為軸向,寬度方向為橫向,分別用x,y表示.張應力退火引起合金薄帶軸向伸長同時橫向收縮,由于受測量精度限制,厚度方向未觀測到明顯的形變發生,因此本文僅考慮x和y方向的形變進行討論.圖1(a)為170 MPa 張應力退火過程合金薄帶軸向宏觀應變曲線,可見升溫前期(b—c)應變緩慢增大到0.0045;然后從633 s 開始偏離線性急劇增大,直至1733 s時達到最大值0.047(c—d).b—c 和c—d 兩部分應變表現出明顯的差異,可能與非晶基底的玻璃化轉變有關,圖1(a)中插圖(圓圈標注區放大圖)定義應變開始偏離線性時的溫度為玻璃轉變點(Tg=426 ℃),在玻璃轉變點以下應變主要是剛性的彈性應變,而在玻璃轉變點以上主要是非均勻的塑性應變.保溫中后期(d—e)應變保持0.047 的穩定值直至保溫結束,已有研究表明[30],Fe 基合金在保溫中后期形成納米晶鑲嵌于非晶基底的雙相結構,納米晶的形成減少了非晶流變單元[31]的自由體積,從而導致非晶基底塑性應變硬化,這可能是應變保持恒定的原因.降溫階段(e—f)應變以先快后慢的速率減小并趨于0.044 的穩定值.卸載載荷階段(f—g)應變從0.044 線性減小至0.041,即卸載載荷引起6.82%的應變以彈性的形式恢復,表明張應力退火過程薄帶軸向應變主要是非均勻的塑性應變.圖1(b)為退火過程薄帶軸向應變速率曲線,其中尖銳的正峰表示合金薄帶軸向應變速率在晶化溫度附近出現極大值.彌散的負峰表示降溫初期熱膨冷縮效應使薄帶軸向應變減小,因此導致應變速率變為負值且形成彌散的負峰.卸載階段線性的應變速率表示彈性應變的恢復過程.

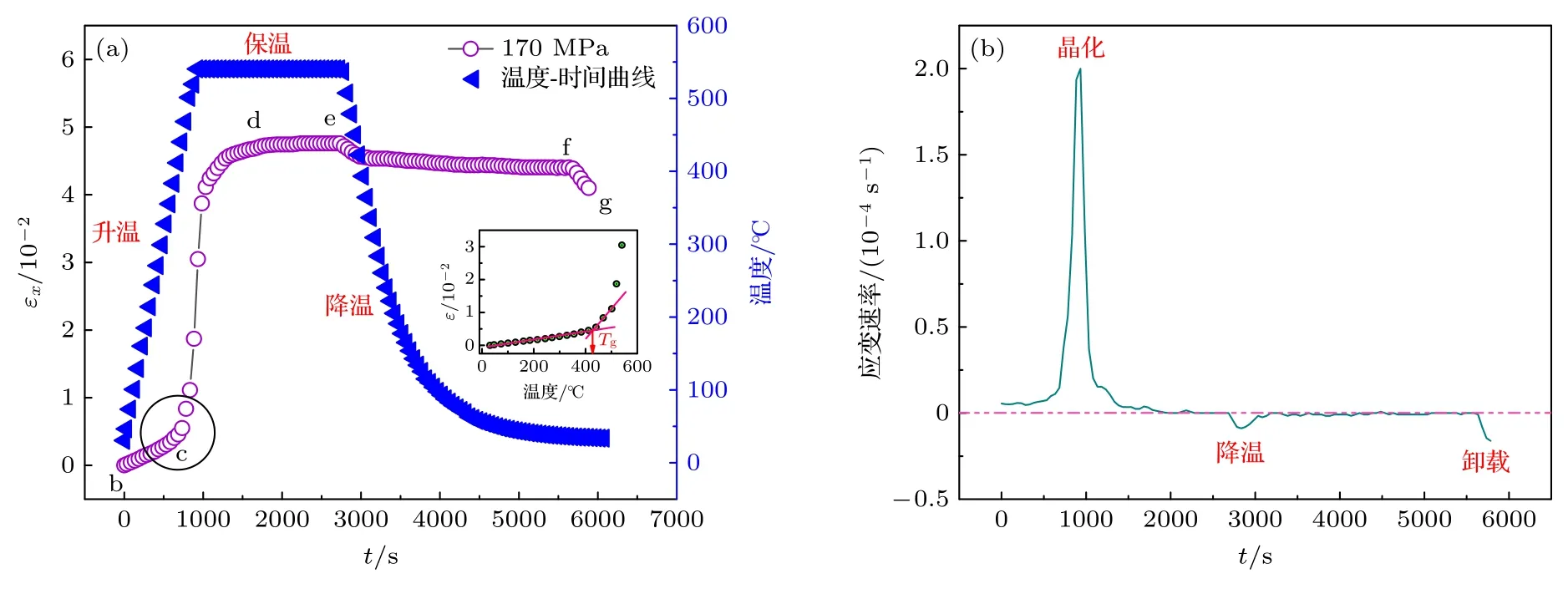
圖1 張應力退火過程Fe 基合金應變及應變速率曲線 (a) 應變;(b)應變速率Fig.1.Strain and strain rates curves of Fe-based alloy ribbons during tensile stress annealing: (a) Strains;(b) strain rates.

圖2 為張應力退火Fe 基合金薄帶的殘余宏觀應變與應力關系曲線,可見殘余應變以非線性的規律隨退火張應力變化.如圖2(a)和圖2(b)所示,當張應力小于223 MPa 時,軸向應變和橫向應變隨張應力線性變化.然而,當張應力大于223 MPa時卻失去了線性變化特征.對圖2 實施數值擬合得函數表達式為

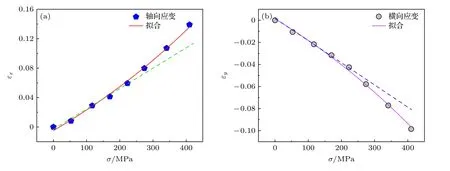
圖2 張應力退火Fe 基合金殘余應變與應力關系曲線 (a) 軸向;(b)橫向Fig.2.Residual macro-strains of Fe-based alloy ribbons as a function of annealing tensile stress: (a) Axial direction;(b) transverse direction.

式 中σc(ε)=800MPa,εx0=0.215和εy0=0.146為擬合常數.σc(ε) 具有應力單位量綱,文中將其定義為與材料某種力學性能相關的應力常數,反映殘余宏觀應變隨應力變化的快慢程度,其值越大則殘余應變變化越慢,相反則變化越快.

圖3(a)為張應力退火Fe 基合金薄帶的LDGMI效應,可見隨退火張應力的增大,LDGMI 曲線由尖銳的“單峰”狀轉變為頂部平坦的“平原”狀.最大巨磁阻抗比以先快后慢的速率減小,同時LDGMI曲線逐漸寬化且出現平頂,表明張應力退火誘導感生的磁各向異性隨退火張應力的增大而增大.圖3(b)為退火誘導感生的磁各向異性K與退火張應力σ的函數關系,可見在小應力下K以線性規律變化,然而在大應力退火下K表現出偏離線性的變化特征.已有研究表明[18,19],張應力退火Fe 基合金薄帶形成α-Fe(Si)納米晶鑲嵌于非晶基底的雙相結構,這種結構使得α-Fe(Si)納米晶晶格彈性應變得以保留.較普遍的觀點認為,α-Fe(Si)納米晶的LPA 是張應力退火誘導感生磁各向異性的微觀結構起源[16,20].為了解SMA 和LPA 間的相關性,本文分別對SMA 和LPA 的弛豫動力學行為進行討論.

3.2 磁各向異性和晶格各向異性的弛豫行為

SMA 可調制優化材料的軟磁性能以滿足不同應用要求,較普遍的觀點認為,張應力退火誘導感生的磁各向異性是由α-Fe(Si)納米晶的晶格彈性應變所致,這種彈性應變可通過回火的方式消除以達到消除SMA 的目的[13,14,17].圖4 為170 MPa 張應力退火Fe 基合金薄帶SMA 的弛豫動力學曲線,文中定義歸一化的磁各向異性為κ=Hk(n)/Hk(0),Hk(n)為經n次回火處理后薄帶的磁各向異性,Hk(0)為張應力退火感生的磁各向異性.采用logistic 擬合得SMA 的弛豫動力學遵循如下規律:

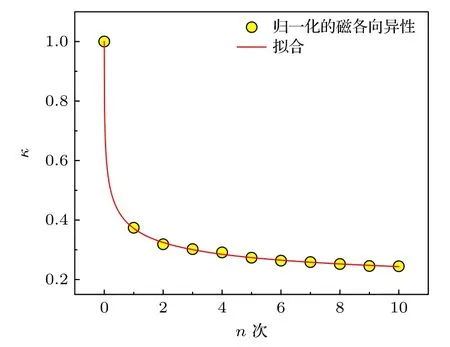
圖4 Fe 基合金薄帶SMA 的弛豫動力學曲線Fig.4.Relaxation dynamics curve of SMA in Fe-based alloy ribbons.

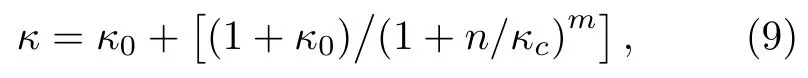
式中κ0,κc和m為擬合常數.由(9)式可知,當回火次數n →∞時,κ →κ0=0.144,表明張應力退火誘導感生的磁各向異性通過回火的方式無法完全消除,仍然有14.4%的磁各向異性永久殘留.

材料磁各向異性的弛豫行為與其微觀結構的弛豫行為密切相關.為闡明兩者間的相關性,本文對自由退火、張應力退火及多次回火處理Fe 基合金薄帶實施SRXRD 衍射實驗,利用FIT2D 軟件對衍射矢量分別平行于帶軸向和橫向的平面譜進行小角度積分,獲得如圖5(a)和圖5(b)所示具有不同物理時效(退火、回火)作用的SRXRD 譜.可見張應力退火使α-Fe(Si)納米晶(200)晶面衍射峰在平行帶軸向往低角度偏移,相反在平行帶橫向往高角度偏移,表明α-Fe(Si)納米晶(200)晶面間距沿帶軸向增大,同時沿帶橫向減小.經多次回火處理發現(200)晶面衍射峰逐漸往自由退火(200)晶面衍射峰位偏移,且當回火次數n=140 時,軸向和橫向(200)晶面衍射峰基本與自由退火重合.圖6為Fe 基合金納米晶LPA 的弛豫動力學曲線,定義歸一化的LPA 為γ=?d(n)/?d(0) ,其中?d(n)=dx(n)?dy(n)為n次回火處理納米晶的LPA,?d(0)=dx(0)?dy(0)為張應力退火(n=0)納米晶的LPA,dx和dy為衍射矢量分別平行于軸向和橫向時(200)晶面間距.對歸一化的LPA 實施logistic 數值擬合,發現LPA 的弛豫動力學遵循如下規律:

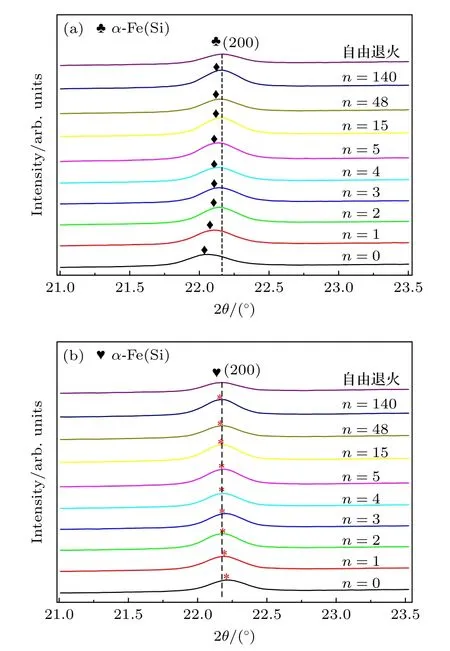
圖5 張應力退火及回火Fe 基合薄帶XRD 譜 (a)軸向;(b)橫向Fig.5.The XRD patterns of Fe-based alloy ribbons annealed with tensile stress and isothermal tempered treatment: (a) The diffraction vector is parallels to ribbon’s axial direction;(b) the diffraction vector is parallels to ribbon’s transverse direction.

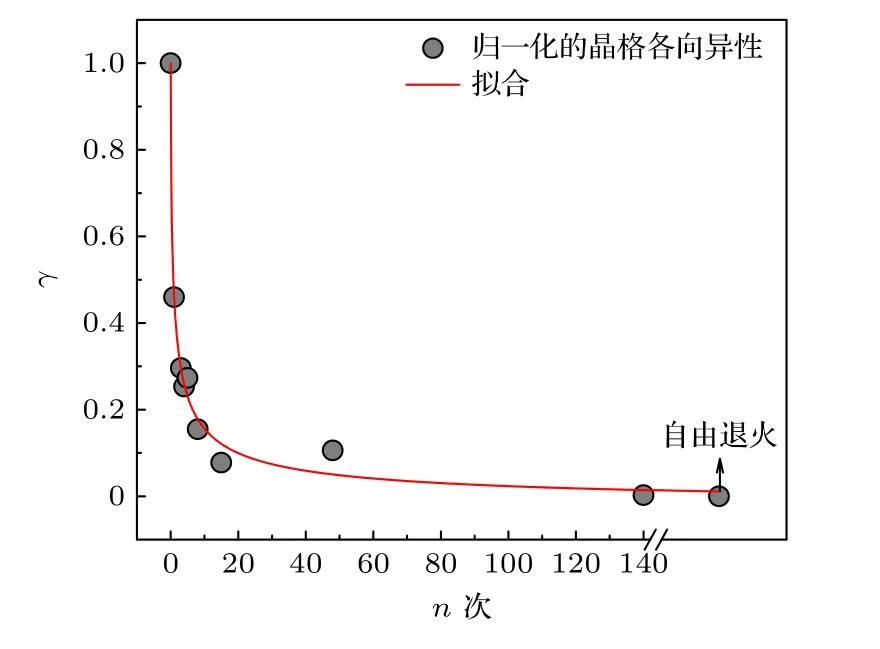
圖6 Fe 基合金LPA 弛豫動力學曲線Fig.6.Relaxation dynamics curve of LPA in Fe-based alloy ribbons.

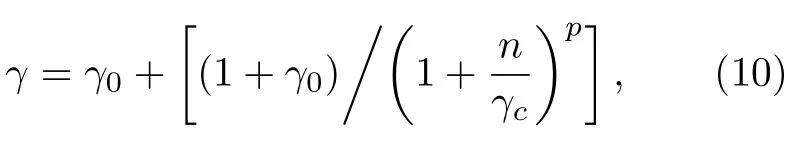
式中γ0,γc和p為擬合常數,當n →∞時,γ →γ0≈0,表明LPA 可通過回火的方式完全消除,即α-Fe(Si)納米晶的LPA 由各向異性變為各向同性.結合SMA 和LPA 的弛豫動力學,發現SMA 由兩部分磁各向異性組成,其中一部分可通過回火的方式消除(可逆),另一部分不能通過回火的方式消除(不可逆).研究表明,Fe 基合金應力感生可逆的磁各向異性起源于α-Fe(Si)納米晶的LPA[27].張應力退火引起合金薄帶主要發生不可逆的塑性形變,它可能會導致鑲嵌于非晶基底的納米晶在空間的分布出現各向異性.

3.3 分布各向異性模型

本文以自由退火Fe 基合金納米晶各向同性分布結構為參考模型,假設直徑為D的納米晶以平均間隙δ0均勻分布于非晶基底,晶化分數為vcr.任選一晶粒為參考點,則與該晶粒相鄰為δ0+D的空間范圍內納米晶的晶化分數可近似表示為

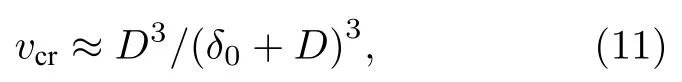
則晶粒平均間隙δ0為

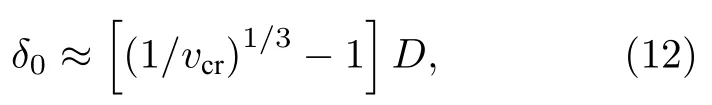
可見晶粒平均間隙δ0與晶化分數vcr和晶粒尺寸D相關.圖7(a)為自由退火Fe 基合金薄帶的SRXRD譜,對其實施峰分析及擬合處理,扣除儀器展寬后結合謝樂公式計算α-Fe(Si)納米晶的平均直徑.取SRXRD 譜的(110)峰,采用如圖7(b)所示的分峰擬合和Pseudo-Voigt 方法計算納米晶晶化分數,相關結構參數如表1 所列.將α-Fe(Si)納米晶結構參數代入(12)式得自由退火Fe 基合金納米晶平均間隙δ0≈2.75 nm.

表1 自由退火Fe 基合金薄帶的結構參數Table 1.Structural parameters of Fe-based alloy ribbons annealed without tensile stress.

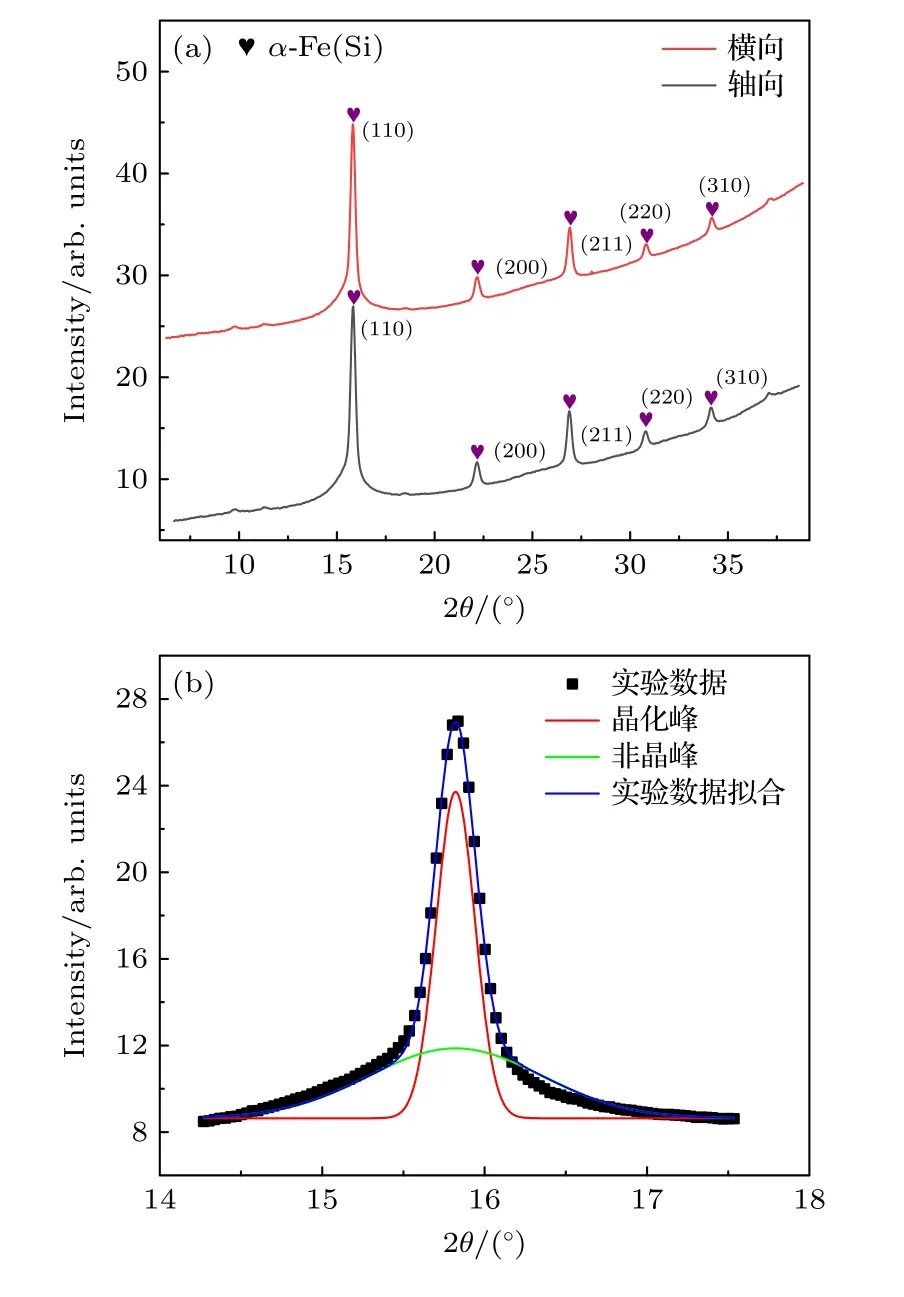
圖7 自由退火Fe 基合金薄帶SRXRD 圖譜 (a)全譜(3°—38°);(b) (110)分峰擬合Fig.7.The SRXRD patterns of Fe-based alloy ribbons annealed without tensile stress: (a) The full spectrum diagram of SRXRD (3°—38°);(b) the multi-peaks fitting of(110) diffraction peak.

現將張應力退火對納米晶分布狀態的影響視為是在各向同性均勻分布結構的基礎上(自由退火),張應力使納米晶晶間距離(平均間隙)在平行應力方向(帶軸向)增大,同時在垂直應力方向(帶橫向)減小.結合宏觀殘余應變測量,忽略張應力退火對納米晶形狀和晶化分數的影響,則張應力退火納米晶在帶軸向和橫向的平均間隙分別表示為

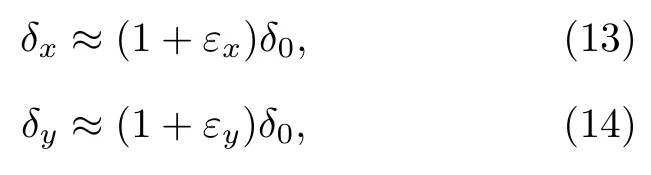
則NGDA(帶軸向和橫向平均晶粒間隙差)可定義為

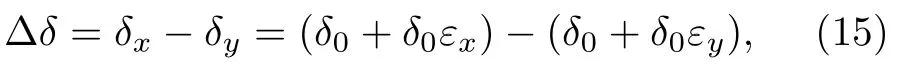
將(7)和(8)式代入(15)式得

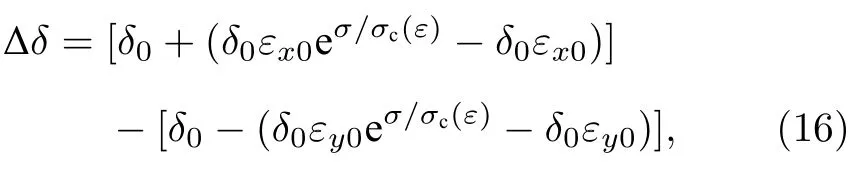
式中右邊第一部分圓括號表示晶粒間隙在帶軸向的增加量,而第二部分圓括號表示晶粒間隙在帶橫向的減小量.(16)式為NGDA 的數學表達式,描述NGDA 和退火應力間的函數關系,其中σ=0 MPa時,?δ=0 nm 表示自由退火納米晶的各向同性分布;σ >0MPa 時,?δ >0 nm 表示張應力退火納米晶的各向異性分布;σ <0MPa 時,?δ <0 nm表示壓應力作用所導致納米晶的各向異性分布.將(16)式變形為

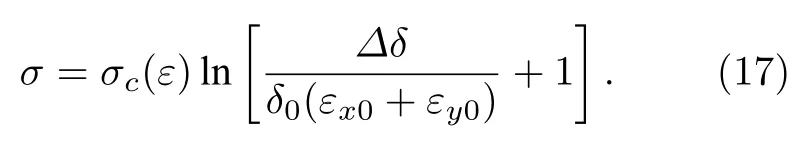
則該式是(16)式的反函數形式.

表2 為張應力退火Fe 基合金薄帶的結構和磁學參數,其中Hk為張應力退火感生的磁各向異性場(從圖3(a)測量獲得),K為SMA(由(3)式計算獲得),Kd為不可逆的SMA,Ke為可逆的SMA.由SMA 的弛豫動力學知,SMA 中包含可逆和不可逆的SMA,其中不可逆的SMA 占14.4%.因此,本文將不同張應力退火誘導感生的磁各向異性K分別乘以系數0.144 便計算獲得不可逆的SMA,將其與張應力的關系繪成如圖8 所示的曲線,實施非線性指數擬合得函數表達式為

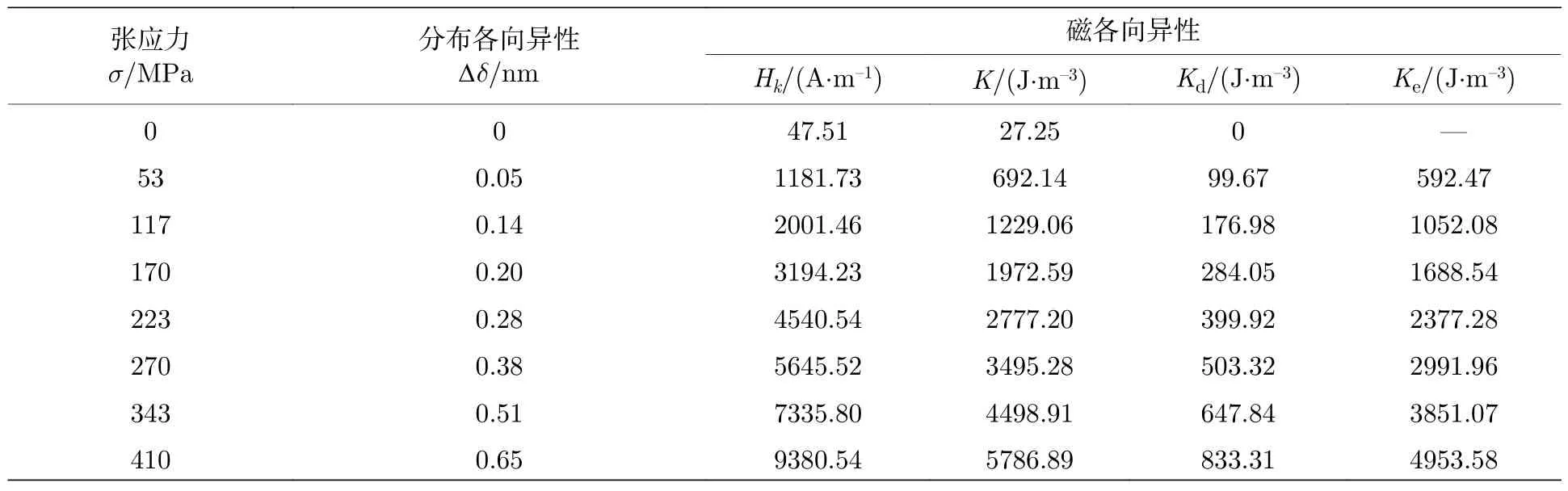
表2 張應力退火Fe 基合金薄帶結構和磁學參數Table 2.Structural and magnetic parameters of Fe-based alloy ribbons annealed with different tensile stress.

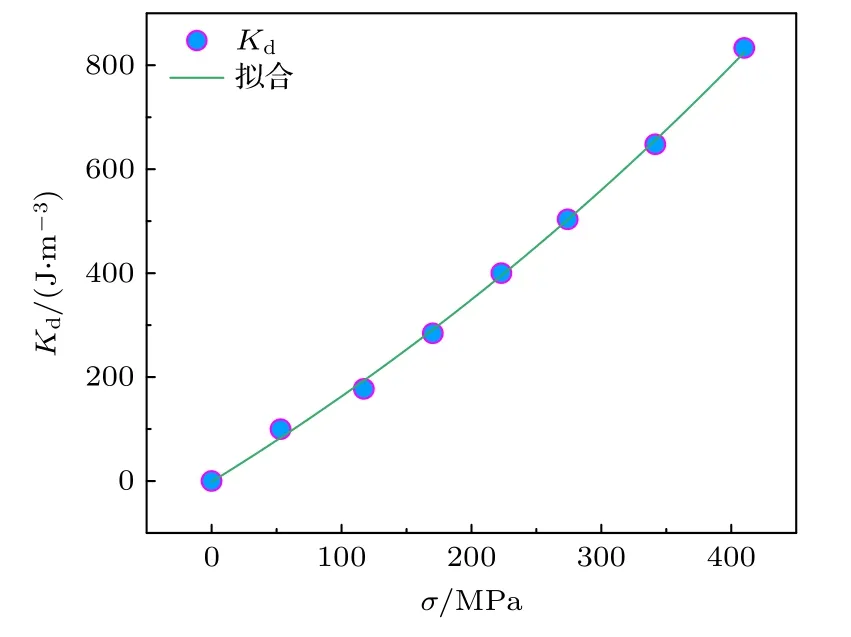
圖8 NGDA 誘導感生磁各向異性與應力關系曲線Fig.8.Dependence of the magnetic anisotropy induced by NGDA on tensile stress in Fe-based alloy ribbons.

式中K0=1235.70J/m3,σc(K)=800 MPa 為擬合常數.將(17)式代入(18)式并變形得

可見Kd與 ?δ呈線性正相關,k為由Fe 基合金結構參數、力學參數和磁學參數共同決定的耦合常數,其具體的物理含義尚需進一步深入研究.由(20)式知,當 ?δ >0時,Kd>0 表明張應力退火感生易磁化方向趨于帶橫向的不可逆磁各向異性;當?δ <0時,Kd<0 表明壓應力感生易磁化方向趨于帶軸向的不可逆磁各向異性.因此,張應力退火Fe 基合金誘導感生不可逆的SMA 可歸因于NGDA,這為理解SMA 機理提出了新見解.

綜上所述,本文借助動態的應變測量技術,檢測張應力退火Fe 基合金薄帶的宏觀應變,討論張應力退火過程宏觀應變的演變規律及殘余應變與退火張應力間的函數關系.隨后從宏觀和微觀兩個層面分別研究了SMA 和LPA 的弛豫動力學,實驗結果和數值擬合預測發現SMA 弛豫達到κ=0.144的穩態值,而LPA 弛豫達到γ ≈0 的穩態值,表明SMA 由可逆的磁各向異性和不可逆的磁各向異性組成.此外,結合張應力退火合金薄帶殘余應變與張應力間的函數關系,以自由退火納米晶各向同性分布結構為參考模型,構建張應力退火Fe基合金NGDA 模型.基于SMA 的弛豫動力學和數值擬合,建立函數描述NGDA 和不可逆的SMA間的依賴性.本文認為張應力退火感生可逆的磁各向異性歸因于納米晶的LPA,而感生不可逆磁各向異性歸因于NGDA.因此,SMA 可表示為

表明納米晶LPA 和NGDA 的協同作用是張應力退火誘導感生磁各向異性物理起源.

4 結論

基于動態的應變測量、LDGMI 效應和同步輻射XRD 衍射,探討張應力退火Fe 基合金SMA 的物理起源.以自由退火納米晶各向同性分布結構為參考模型,構建張應力退火Fe 基合金NGDA 模型,結合SMA 和LPA 弛豫動力學及數值擬合建立不可逆SMA 與NGDA 間的函數關系,為理解SMA機理提出了新的見解.結果如下:

1)張應力退火過程,宏觀應變在玻璃轉變點以下主要表現為彈性應變,在玻璃轉變點以上主要表現為非均勻的塑性應變,而納米晶的析出使非晶基底塑性應變硬化,導致應變速率減緩并趨于飽和.

2) SMA 和LPA 表現出不同的弛豫動力學,前者可通過無限次回火達到κ=0.144 穩態值,而后者僅通過有限次回火便達到γ ≈0 的穩態值,表明SMA 由可逆的磁各向異性和不可逆的磁各向異性組成.

3)構建NGDA 模型,應力感生不可逆磁各向異性與NGDA 呈線性正相關,且滿足Kd=k?δ的函數關系,主張應力退火感生不可逆磁各向異性起源于NGDA.

本研究認為LPA 和NGDA 的協同作用是SMA的物理起源,NGDA 模型的建立為不可逆的SMA提供了解釋,這對深入理解SMA 的機理具有重要的指導意義.