尺寸依賴的CoCrFeNiMn 晶體/非晶雙相高熵合金塑性變形機制的分子動力學模擬*

安敏榮 李思瀾 宿夢嘉 鄧瓊? 宋海洋?

1) (西安石油大學新能源學院,西安 710065)

2) (西安石油大學材料科學與工程學院,西安 710065)

3) (西北工業大學航空學院,西安 710072)

晶體/非晶雙相高熵合金是近年來研究人員提出的獲得高強高韌高熵合金的有效策略,其塑性變形機制和組成相的尺寸密切相關.本文采用分子動力學模擬方法研究了組成相尺寸對CoCrFeNiMn 晶體/非晶雙相高熵合金塑性變形機制的影響.研究表明,非晶相尺寸對雙相高熵合金的力學行為和塑性變形機制有顯著影響.對于非晶相厚度較小的樣品,塑性變形是位錯滑移和面心立方向六方密排結構的相變主導的,尤其是在非晶厚度為1 nm 的樣品中觀察到了孿晶和位錯鎖;非晶相厚度適中時,雙相高熵合金主要通過晶體相中位錯滑移、面心立方向六方密排結構的相變和非晶相的剪切帶增殖來實現塑性變形;非晶相厚度較大時,雙相高熵合金的塑性變形則由非晶相中均勻剪切帶的形成主導.此外,非晶相厚度的增加對位錯的形核和發射有延遲作用,并且,晶體/非晶雙相結構中的非晶相有穩定晶粒的作用.本文的研究結果對于設計和制備高性能的高熵合金具有一定的科學價值和指導意義.

1 引言

高熵合金(high-entropy alloy,HEA)[1?5]是近年來提出的一種新的合金設計理念,它打破了傳統合金中以1 種或2 種元素為主、輔以極少量其他元素來改善合金性能的傳統思想,是由多種元素以等原子比或近似等原子比混合后形成的具有獨特原子結構特征的單一固溶體合金.HEAs 已經展示了優異的力學性能,如高強、高硬、高塑性、抗高溫軟化、抗輻照、耐磨等[6?10].從傳統固溶相結構出發,HEAs 可分為單相面心立方(face-centered-cubic,FCC)、體心立方(body-centered-cubic,BCC)或六方密排(hexagonal-close-packed,HCP)的晶體結構[6].而單相高熵合金仍未徹底解決傳統單相金屬材料高強度和高韌性的權衡問題.例如,室溫下最典型的FCC 結構高熵合金CoCrFeNiMn 斷裂延伸率可達50%,而屈服強度只有約410 MPa[11];單相BCC 結構高熵合金TaHfZrTi 的拉伸強度高達1.5 GPa,但其塑性只有大約4%[12].為了獲得高強高韌的高熵合金,研究者們做出了大量努力與嘗試.例如,通過固溶強化、位錯強化、細晶強化、第二相粒子強化以及滲碳滲氮強化以及鍍膜強化等[13?15]方式來提升高熵合金的綜合力學性能,但提升效果還不能滿足人們對高性能高熵合金的預期要求.因此,尋求一種新型的高熵合金設計理念,實現其高強度和高韌性的有效結合,是目前高熵合金領域亟需解決的難題.

非晶合金又被稱為金屬玻璃,它兼有金屬和玻璃的特性,具有極高的屈服強度和良好的耐磨性能,但是由于其內部沒有晶粒、晶界、位錯以及層錯等缺陷,受載后可能呈現出災難性的脆性斷裂,嚴重制約了非晶合金的廣泛應用[16,17].近年來,研究人員做了大量努力來改善非晶合金的塑性,其中一種有效的策略是在非晶相基體中加入晶體相[18?22].研究表明,在非晶合金基體中引入晶體相來調控其塑性進行時,晶體/非晶界面(crystal/amorphous interface,CAI)既可以誘發剪切帶的成核,又可以阻礙非晶相中剪切帶的擴展;同時,CAI 既可以吸收晶體中的位錯,也可以充當位錯源以促進位錯形核與發射,從而有效提升非晶合金的力學性能[19].基于此種策略,Wu 等[10]在2020 年開發出了兼顧強度和韌性的CrCoNi-Fe-Si-B 納米晶體/非晶雙相HEAs,它的屈服強度接近于理論值(G/24,G為材料的剪切模量),壓縮均勻塑性形變更是超過了45%.他們指出HEAs 的高強度源自于晶體/非晶雙相結構、界面-位錯交互作用、晶體及非晶相的納米級尺寸單元和晶體相內的超高密度孿晶.高塑性則源于非晶相的塑性流變、晶體相內的不全位錯運動等.同年,Xiao 等[21]也研究了晶體/非晶雙相CoCrFeNiMn 高熵合金的力學性能,他們發現改變晶體相和非晶相的厚度可以調節位錯與CAI 的相互作用,從而改變合金的強度.這些實驗結果證明,通過調控晶體相與非晶相的尺寸,可以有效地促進晶體相和非晶相的協同作用,從而獲得兼顧高強度和高韌性的晶體/非晶雙相高熵合金.

Jiang 等[23]利用磁控濺射方法制備了CrMnFe CoNi 和TiZrNbHfTa 高熵合金交替排列的納米多層膜.微觀結構表征發現,在層厚度為50 nm 時,TiZrNbHfTa 合金為非晶結構而CrMnFeCoNi 合金為FCC 晶體結構.納米壓入測試表明這種晶體/非晶納米多層膜兼備了高硬度(5.6 GPa)和較好的塑性變形能力,這同樣歸功于非晶層和晶體層在材料塑性變形過程中的協調作用.與傳統的均勻密度非晶固體相比,TiZrNbHfTa 非晶層可以發生更均勻的塑性變形,從而有效地降低了壓痕周圍剪切帶的密度;而高強度則是與CoCrFeMnNi 晶體層中高密度的層錯和納米孿晶以及非晶態結構密切相關.由于目前的實驗手段對于材料在變形過程中的微觀結構演化的觀測仍存在諸多挑戰,分子動力學則開辟了一條新的途徑,它可以詳細描述材料在塑性變形過程中的微觀結構演化,關于雙相高熵合金人們也做了一些模擬方面的工作[24,25].Li 等[24]研究了CoCrFeNi 晶體/非晶雙相復合材料在拉伸載荷下的力學性能.研究表明,晶體/非晶雙相HEAs 復合材料表現出較好的塑性,但是強度隨著非晶層厚度的增加而降低.該雙相HEAs 復合材料的高塑性歸因于晶體相和非晶相之間的塑性協同作用.Zhou 等[25]研究了CoCrFeNiMn HEA 晶體/非晶雙相復合材料在不同溫度下的拉伸力學行為.研究表明,雙相復合材料的塑性變形機制與溫度和非晶相厚度密切相關.在1—800 K 溫度范圍內,這種雙相復合材料模型有效地抑制了位錯發射和晶界主導的變形;對于非晶厚度較小的模型,其塑性主要由晶體相主導,非晶相可以防止晶界引發的晶粒變形,從而提高雙相HEA 復合材料的強度;對于非晶相厚度較大的模型,非晶相的塑性流動主導了材料的塑性變形過程.上述研究結果表明,通過調控晶體/非晶雙相高熵合金中組成相的尺寸可以有效地控制材料的塑性變形機制.

基于以上原因,本研究擬采用大規模分子動力學模擬方法研究晶體/非晶雙相HEAs 的力學性能和塑性變形行為.具體研究時,選擇CoCrFeNiMn晶體/非晶雙相高熵合金為研究對象.這主要是由于低層錯能的FCC 晶體結構CoCrFeNiMn HEAs在特定條件下呈現出奇特的“既強且韌”趨勢,但對其塑性變形機制和強韌化機理還存在諸多爭論[26?28].因此,本研究利用分子動力學方法研究了CoCrFeNiMn 晶體/非晶雙相高熵合金在室溫下的力學性能和塑性變形行為.結果表明雙相HEAs的力學行為和塑性變形機制依賴于組成相的尺寸.非晶相較厚的樣品中,非晶相的塑性承載能力較好,模型的塑性變形機制為非晶相的剪切帶增殖;非晶相厚度適中時,模型的塑性變形主要是晶體相中的位錯滑移、FCC 與HCP 相的轉變和非晶相的剪切帶增殖主導;而非晶相厚度較小時,模型主要通過位錯滑移和相變進行變形.本文的研究結果對于設計和制備高性能的HEAs 具有一定的科學價值和指導意義.

2 模擬方法和模擬過程

采用LAMMPS (large-scale atomic/molecular massively parallel simulator)軟件[29]模擬了CoCr FeNiMn 晶體/非晶雙相HEAs 在室溫(300 K)下的拉伸力學性能.圖1 為非晶厚度h為1 nm 的CoCrFeNiMn 晶體/非晶雙相HEA 的示意圖,從圖1(a)可看出,Co,Cr,Fe,Ni 和Mn 五種元素均勻地分布在高熵合金中.基于Xiao 等[21]的實驗結果,初始模型為包含四個六邊形柱狀晶粒的多晶模型.模型的尺寸為36 nm×42 nm×3.5 nm,其中晶粒1 的三維方向分別是包含約460000 個原子.為了避免孿晶出現,模型中4 個晶粒分別繞著Z軸旋轉0°,30°,60°和90°,這和Cao 與Wei[30]和Yamakov 等[31]的模型構建方式是一致的.隨后,保持模型的整體尺寸不變,通過選擇不同的非晶厚度h=1,3,5,7,9 和11 nm 來研究雙相HEAs 中非晶相尺寸對其力學性能的影響.相應地,晶粒的尺寸d也隨著非晶相厚度變化而變化,從17 nm 降低到7 nm.分子動力學模擬構建非晶相的過程如下: 1) 對建立的FCC 結構CoCrFeNiMn HEA 模型在零壓下逐漸加溫至2500 K 使之熔化;2) 在零壓下以1013K/s的速率快速淬火至300 K;3) 在300 K 的溫度弛豫50 ps (10–12s)以消除系統熱波動,最終得到較為穩定的非晶相[32].在模擬的過程中,沿著X,Y和Z三個方向都施加周期性邊界條件以消除自由表面對于變形的影響.

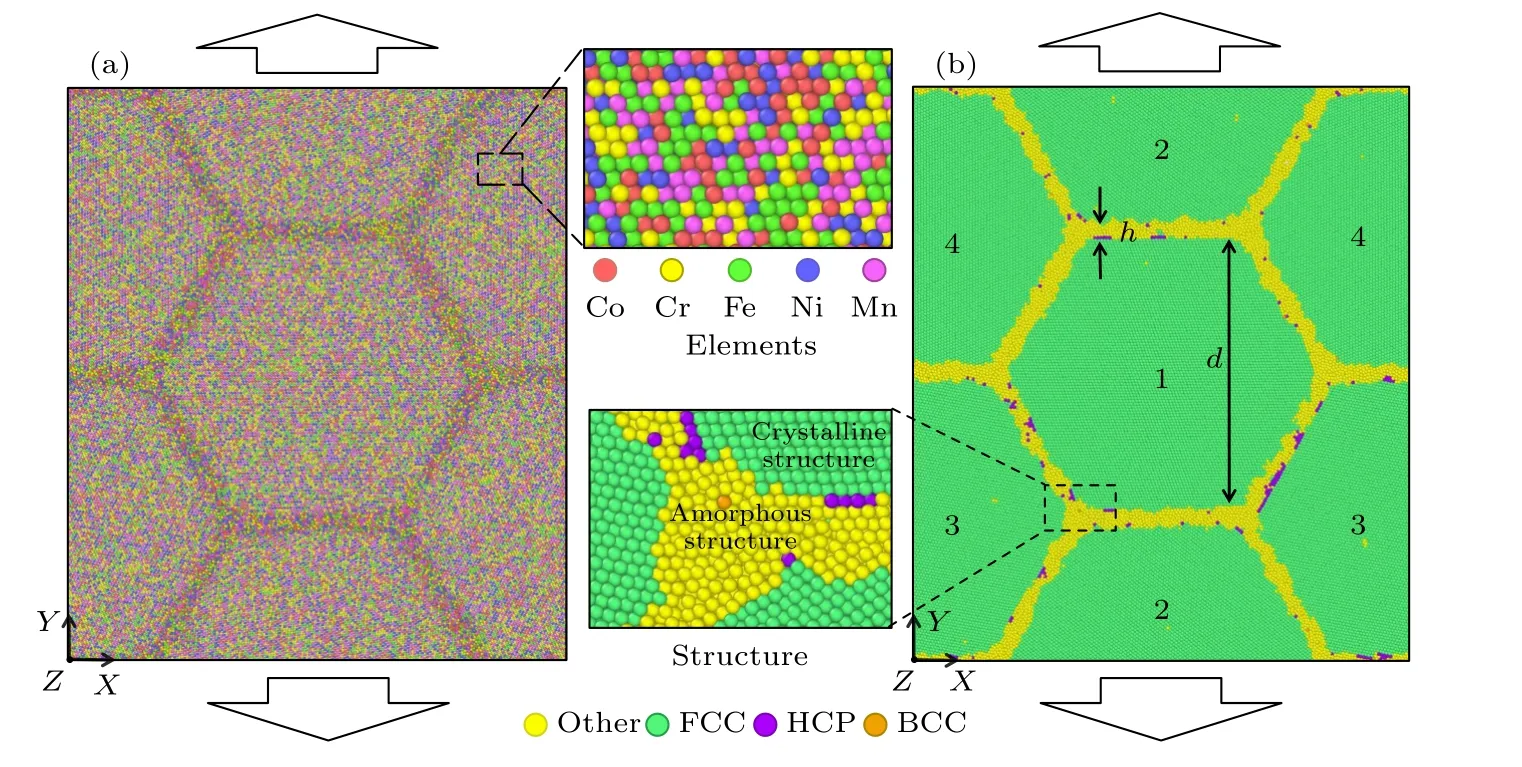
圖1 CoCrFeNiMn 晶體/非晶雙相高熵合金模型 (a) 初始構型;(b) 經公共近鄰分析得到的原子結構圖Fig.1.Schematic of CoCrFeNiMn crystalline/amorphous dual-phase high-entropy alloy: (a) The initial configuration;(b) atomic configuration identified by the common neighbor analysis method.

初始模型構建好之后,對模型沿著Y方向施加均勻拉伸載荷,其應變率為5×108s–1.在模擬過程中應用NPT 系綜,時間步長設為1 fs,模擬溫度選取300 K.采用Choi 等[33]提出的第二近鄰修正嵌入原子勢(the second nearest-neighbor modified embedded-atom method,2NN MEAM),該勢函數已經被證明能夠準確地描述Co,Cr,Fe,Ni,Mn 五種元素之間的相互作用.為了分辨模型中不同的原子結構,采用OVITO (open visualization tool)軟件[34]對模擬結果進行可視化分析,并采用公共近鄰原子分析(common neighbor analysis,CNA)[35]來觀察模型存在的缺陷和原子運動的過程.如圖1(b)所示,其中FCC 結構原子、HCP結構原子和BCC 結構原子分別用綠色、紫色、橙色表示,被識別為“其他(Other)”的黃色原子代表非晶相的原子.

3 結果與討論

室溫下,多晶模型和不同非晶相厚度的雙相HEAs 模型的應力-應變曲線如圖2(a)所示,可以看出,非晶相厚度不同的模型應力-應變曲線的變化呈現出不同變化趨勢.對于多晶模型,在彈性階段應力隨著應變的增加呈現線彈性的增長,當應變增加到0.033 時材料產生屈服,屈服后應力在某一穩態值附近波動.而CoCrFeNiMn 雙相HEAs 模型,非晶相厚度對CoCrFeNiMn 雙相HEAs 模型的變形行為的影響十分顯著.當非晶厚度較小時,例如非晶相厚度h=1,3 和5 nm 的模型,應力到達峰值后即出現較大的跌落,而后應力在某一值附近波動;對于非晶厚度較大的模型如h=7,9 和11 nm,在應力到達峰值之后并未出現迅速跌落,在達到峰值應力后其應力隨著應變的增加幾乎穩定在某一特定值附近,應力和應變之間呈現理想的彈塑性關系.可見,不同非晶相厚度的CoCrFeNiMn雙相HEAs 模型的變形行為發生了變化.為進一步說明雙相HEAs 的力學行為和塑性變形機制依賴于組成相的尺寸,圖2(b)展示了不同非晶厚度樣品的楊氏模量(線彈性階段范圍內,即應變范圍在0—0.03 之間的應力-應變曲線的斜率)的變化趨勢.從圖2(b)可以看出,對于CoCrFeNiMn 雙相HEAs模型,隨著非晶相厚度從1 nm 增加到11 nm,楊氏模量由147 GPa 減小到83.5 GPa,且除了非晶厚度為1 nm 的模型之外其余模型的楊氏模量均低于多晶模型.圖2(c)則展示了峰值應力(應力-應變曲線的第一個波峰處的應力)和平均流動應力(應力-應變曲線的第一個波谷對應的應變至應變為0.30 之間的應力平均值)隨非晶相厚度的關系圖.由圖2(c)可知,峰值應力和平均流動應力均隨著層厚度的增加而減小,這與Zhou等[25]的結論是一致的.需要注意的是,非晶相厚度h=1 nm時,雙相HEA 模型的峰值應力和平均流動應力均高于多晶模型.為了闡述這種現象,下文將通過分析不同模型的微結構演化和塑性變形機制來進一步分析雙相CoCrFeNiMn 模型的尺寸效應.

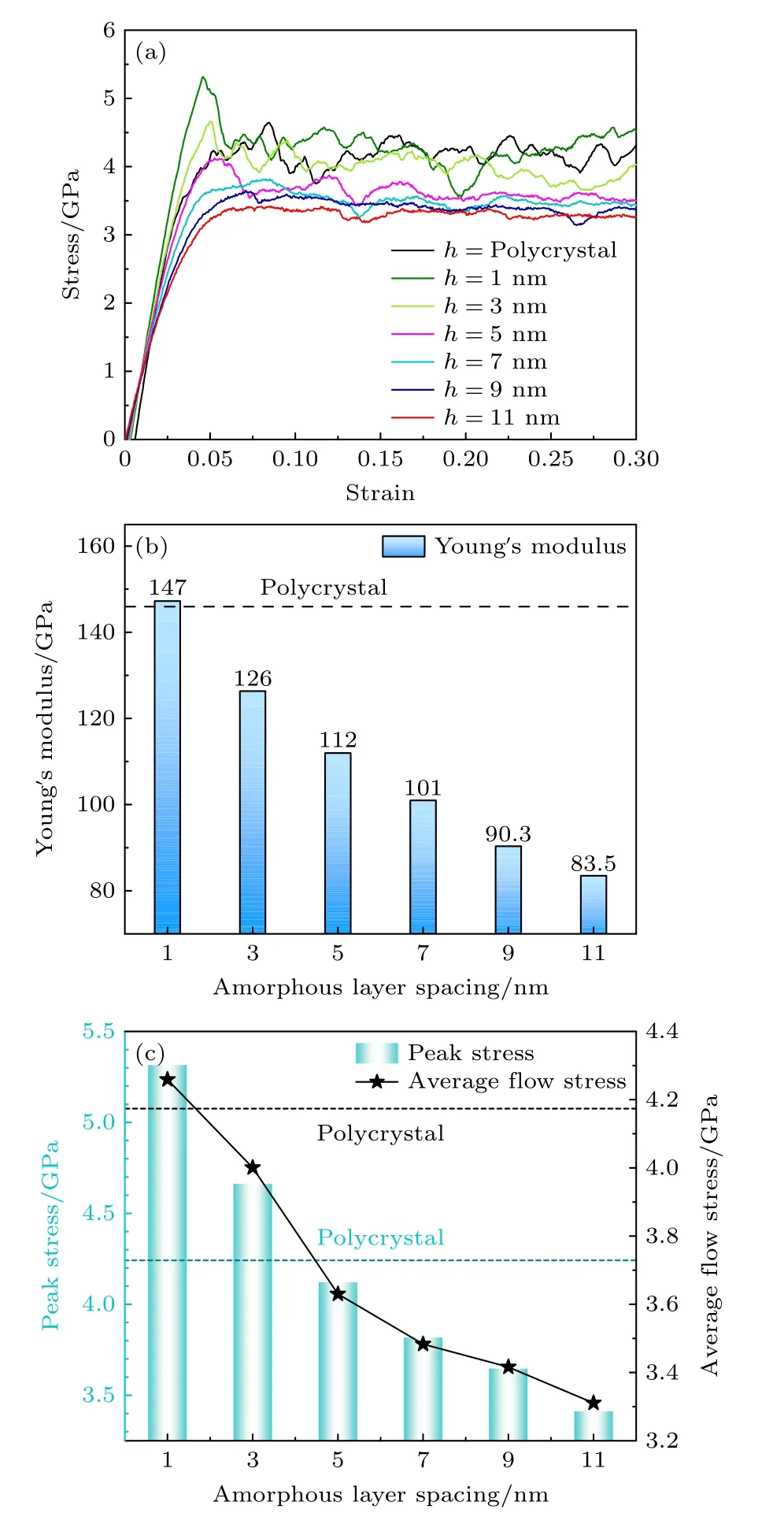
圖2 不同非晶相厚度的CoCrFeNiMn 晶體/非晶雙相高熵合金的拉伸力學性能 (a) 應力-應變曲線;(b) 楊氏模量;(c) 峰值應力和平均流動應力Fig.2.Tensile properties of dual-phase CoCrFeNiMn crystalline/amorphous high-entropy alloys with different amorphous layer spacing: (a) Stress-strain curves;(b) Young’s modulus;(c) peak stress and average flow stress.

作為對照組試驗,圖3 給出了不含非晶相的CoCrFeNiMn 多晶模型在不同應變下的原子結構圖.從圖3 可以看出,當拉伸應變達到0.033 時,位錯在晶粒1、晶粒2 和晶粒4 的交界處形核和發射,如圖3(a)的黑色圓圈所示,該現象也與圖2(a)應力-應變曲線到達屈服點對應.隨后,在拉伸載荷的作用下,大量的位錯不斷從晶界處發射并沿著{111}面特定方向滑移,高密度位錯的滑移在FCC 結構CoCrFeNiMn HEA 中形成了堆垛層錯(stacking faults,SFs),當他們運動到CAI 時會被其阻礙和吸收,完整的界面變成連續的線缺陷,這些連續的線缺陷最終被運動的位錯帶走.圖3(b)的黑色箭頭所指為第一處被破壞的CAI,隨著拉伸載荷的不斷加載,CAI 多處被破壞,被破壞的CAI 不能再有效地阻止位錯的滑移.當應變達到0.200 時,多晶晶界被徹底破壞,其初始結構也不復存在,如圖3(f)所示.值得注意的是,這些SFs 在不斷的積累的過程中形成了HCP 相,如圖3(c)—(f)所示.而當應力跌落至最低點(ε=0.111)時出現了大量的FCC相到HCP 相的轉變,如圖3(e).上述結果表明,多晶模型的塑性變形由位錯滑移和FCC 到HCP 相轉變所主導.

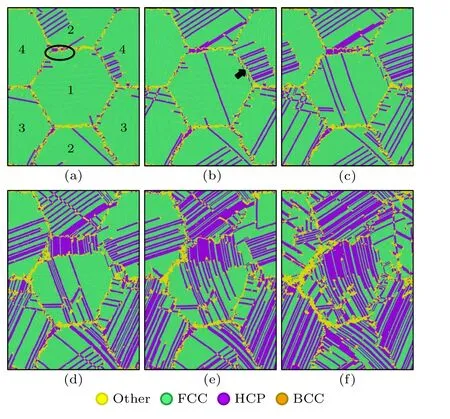
圖3 多晶CoCrFeNiMn 高熵合金在不同拉伸應變時的原子結構演變圖 (a) ε=0.033;(b) ε=0.045;(c) ε=0.057;(d) ε=0.089;(e) ε=0.111;(f) ε=0.200Fig.3.Atomic configuration evolutions of polycrystalline CoCrFeNiMn high-entropy alloy: (a) ε=0.033;(b) ε=0.045;(c) ε=0.057;(d) ε=0.089;(e) ε=0.111;(f) ε=0.200.

為了說明非晶厚度對雙相高熵合金塑性變形機理的影響,圖4 展示了三種具有代表性的CoCr FeNiMn 雙相HEAs 模型(非晶相厚度h分別為1,5 和11 nm)在不同拉伸應變時的原子結構演變圖.圖4 中晶體部分中的原子結構和缺陷是通過CNA 方法來分析的,非晶相的變形行為是通過馮米塞斯應變ηMises來呈現的.通常而言,非晶中沒有類似于晶體中的位錯、孿晶和層錯等缺陷,因此室溫下非晶的塑性變形主要通過剪切帶的形成來實現,即大量塑性變形集中在一條或幾條狹窄的帶狀區域中,因此非晶材料的宏觀塑性較差.剪切帶的形成和傳播機制主要有兩種: 自由體積理論和剪切轉變區域理論,它們從微觀角度說明了剪切帶中原子結構的變化.從圖4(a)—(c)可看出,在拉伸載荷作用下,非晶相中的原子結構發生了重新排布,均出現剪切轉變區域團簇,而此時晶體相都仍處于彈性階段.顯然,雙相HEAs 中非晶相是軟相,其塑性變形始于非晶相中剪切轉變區域的形成和增殖.對于非晶相厚度h=1 nm 樣品,拉伸應變ε=0.034時,由于原子應力集中,Shockley 位錯從晶粒2 的CAI 處形核并發射,如圖4(a1)所示.隨著拉伸加載,非晶相中的剪切轉變區域不斷積累并形成了剪切帶,而晶體中的Shockley 位錯沿著{111}面不斷滑移并形成了SFs.此外,在晶粒2 中觀察到了孿晶,如圖4(a2)中白色圓圈所示.在拉伸載荷下,SFs 一方面不斷地交叉相互作用形成了Lomer-Cottrell 位錯鎖,另一方面不斷積累形成了HCP 相,如圖4(a3)和圖4(a4)所示.由于非晶相厚度較小,剪切轉變區域不能有效擴展,而是在非晶相中形成了較薄的剪切帶.因此,非晶相厚度較小時,雙相HEAs 的塑性變形并不依賴于非晶相中的剪切帶,而是主要通過晶體相中的位錯滑移和FCC 相到HCP 相的轉變進行.h=5 nm 時,非晶相中的剪切轉變區域傳播到相鄰的晶粒并引發了位錯的形核和發射,如圖4(b1)所示,這引發了圖2(a)中粉色應力-應變曲線在達到峰值后的陡然跌落.此時,非晶相厚度適中,剪切轉變區域有了一定的空間增殖并逐漸形成與拉伸方向呈45°的剪切帶胚胎,如圖4(b1)白色圓圈所示.在拉伸作用下,一方面位錯的運動不斷地被CAI 阻礙和吸收,另一方面,非晶相中剪切轉變區域不斷增殖導致剪切帶胚胎區域不斷擴展并形成均勻的剪切帶,如圖4(b2)—(b4)所示,這就解釋了圖2(a)中對應的應力-應變曲線跌落之后在某一特定值附近的波動.因此,非晶相厚度適中時,雙相HEAs 主要通過晶體相中位錯滑移、FCC 相到HCP 相的轉變和非晶相的剪切帶形成來進行塑性變形.h=11 nm 時,其變形主要集中在非晶相中,如圖4(c)所示.在拉伸加載伊始,非晶相中的原子結構發生了重新排布,出現了均勻的剪切轉變區域團簇,當應變增加到0.065 時,晶體相中位錯開始形核并發射,如圖4(c1)中的白色圓圈所示,此時正對應于圖2(a)中紅色應力-應變曲線的首次應力峰值.隨著拉伸應變增加,晶體相中位錯不斷滑移,而非晶相中的剪切轉變區域則不斷增殖并最終形成了均勻的剪切帶,如圖4(c2)—(c4)所示,這就引發了應力在到達峰值之后幾乎穩定在某一特定值附近.值得注意的是,晶體相中雖有一定的位錯滑移,但是由于晶體相比例較小,晶體中位錯滑移的數量也很少.因此,非晶相厚度較大時,雙相HEAs 的塑性變形是由非晶相中剪切轉變區域增殖并最終形成均勻剪切帶的方式主導的.

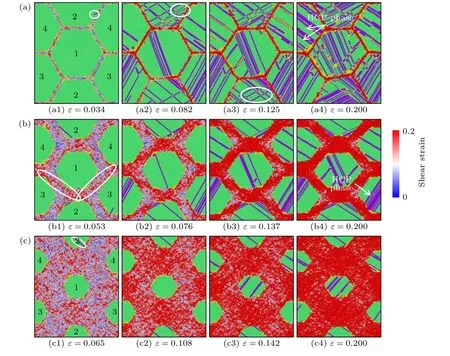
圖4 不同非晶厚度的雙相HEAs 在不同拉伸應變時的原子結構演變圖 (a) h=1 nm;(b) h=5 nm;(c) h=11 nm.圖4(a1)中圓圈代表了位錯發射點,圖4(a2)中圓圈代表孿晶,圖4(a3)中圓圈代表位錯鎖,圖4(b1)中圓圈代表剪切帶的雛形Fig.4.Atomic configuration evolutions of the CoCrFeNiMn crystalline/amorphous dual-phase high-entropy alloys with different amorphous layer spacing: (a) h=1 nm;(b) h=5 nm;(c) h=11 nm.The emission site of the dislocation,the deformation twin and the Lomer-Cottrell locks are depicted by the circles in Fig.4(a1),Fig.4(a2) and Fig.4(a3),respectively.The circle in Fig.4(b1)represents the embryo of the shear band.

此外,對比圖4(a1)、圖4(b1)和圖4(c1)發現,三種不同厚度的CoCrFeNiMn 雙相HEAs 中首個位錯發射時的拉伸應變分別為0.034,0.053 和0.065,這表明非晶相厚度的增加對位錯的形核和發射有延遲作用.并且,晶體/非晶雙相結構中的非晶相有穩定晶粒的作用.例如,h=1 nm 的模型在變形中后期發生了較為明顯的晶粒變形,隨著非晶相厚度的逐漸增加(例如,h=5 nm 和h=11 nm),晶粒的變形越來越不明顯,如圖4(a4)、圖4(b4)和圖4(c4)所示.這與圖3 中多晶中晶粒界面被破壞所導致的晶粒變形完全不同.也就是說,晶體/非晶界面能夠有效抑制晶粒界面介導的變形,這和Zhou 等[25]的研究結論是一致的.此外,隨著非晶相厚度不斷增加,其中剪切轉變區域分布變得更加均勻,CAI 協調塑性變形的能力比常規晶界強得多.因此,晶體相、非晶相以及CAI 的協調運動主導了雙相高熵合金的塑性變形.

為了更直觀地探究不同模型在拉伸載荷下的塑性變形機制,圖5 展示了圖4 所示的三種典型的雙相HEAs 在拉伸過程中的不同結構比例變化情況,其中Other 原子代表非晶相原子.從圖5 可看出,三種HEAs 中非晶相比例在整個變形過程中幾乎沒有發生變化.對于較小非晶厚度(h=1 nm)的樣品,FCC 相比例在拉伸加載伊始高達88%,應變增加至0.035 時FCC 相比例逐漸減少,HCP 相比例呈互補性增加,如圖5(a)所示.這與圖4(a)中位錯滑移、堆垛層錯產生以及FCC→HCP 相變相對應.并且當應變增加至0.20 時,FCC 基CoCr FeNiMn 雙相高熵合金中的HCP 相比例約占32%,這也和圖4(a4)中大量堆垛層錯的累積形成HCP相的結論一致.而中等非晶相厚(h=5 nm)的雙相HEAs,非晶相的比例大約是44%,在拉伸應變增加到0.04 后晶體相中位錯開始形核并轉變成HCP 相,但其轉變速率明顯小于h=1 nm 的模型.當應變增加至0.20 時HCP 相比例約占12%,這與圖4(b4)中少量的HCP 相對應.而對于較大非晶相厚度(h=11 nm)的雙相HEAs 而言,加載伊始其FCC 相的比例約為20%,塑性變形過程中有少量位錯滑移和SFs,當應變增加至0.20 時,HCP相比例約占3%,這也與圖4(c4)中晶體的微觀變形結果相對應.隨著應變的增加,三種HEAs 中BCC 結構原子的比例幾乎不變,均穩定在0.03%—0.7%附近.這就意味著,在整個變形過程中BCC的比例很小,可以忽略不計.實際上,BCC 結構原子出現是由于嚴重的晶格畸變和較高的局部應變效應所引起的臨界應力超過基體中BCC 相成核所需的應力引發的[36],這種現象在Li 等[24]的研究中也被觀察到了.所以,BCC 結構對變形機制的影響可以忽略.

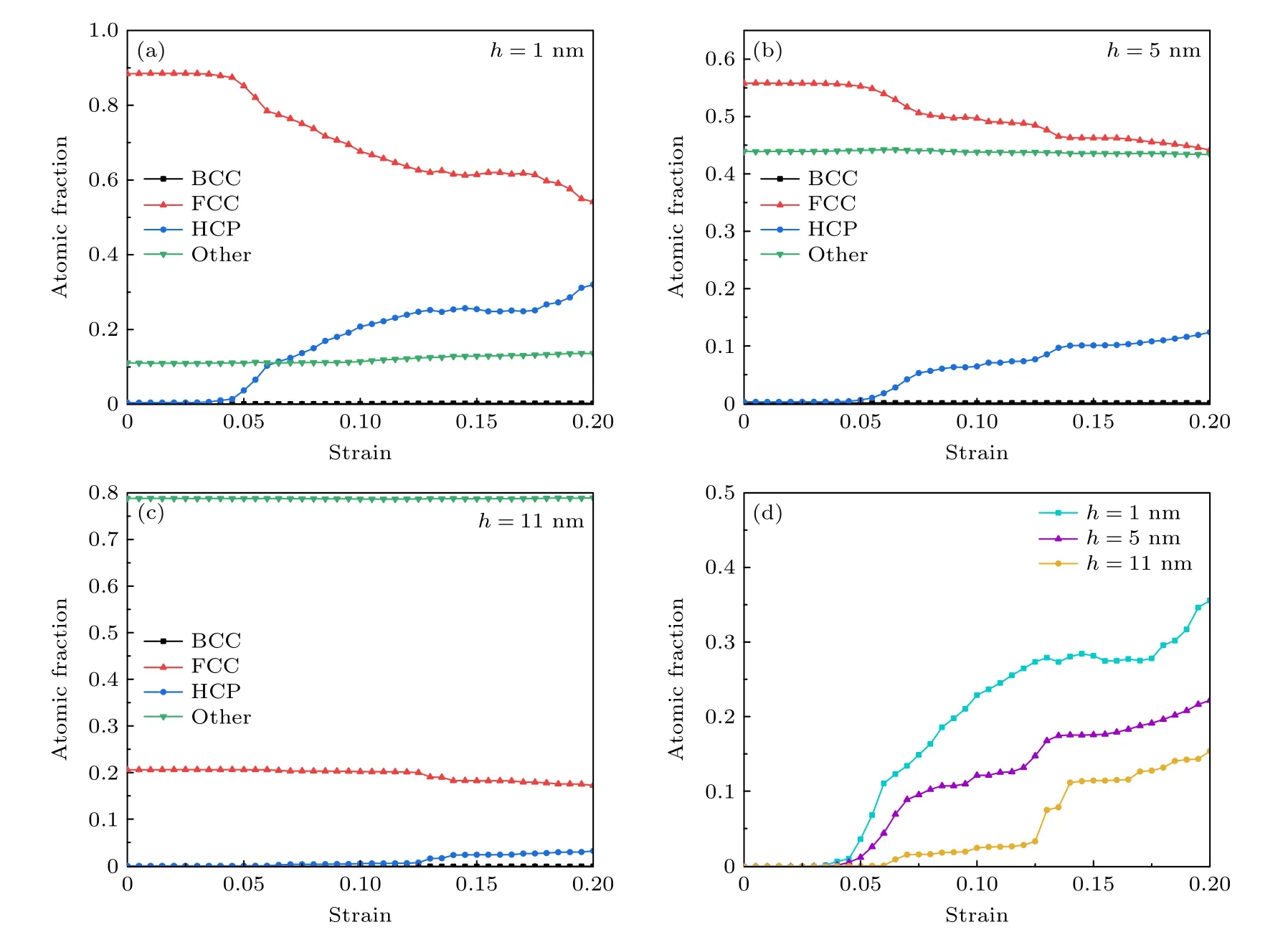
圖5 不同非晶厚度的雙相HEAs 在拉伸過程中的不同結構原子比例變化圖,其中(a) h =1 nm,(b) h =5 nm,(c) h =11 nm;(d) FCC 相轉變為HCP 相的原子分數Fig.5.Atomic fraction evolutions of different structures of the CoCrFeNiMn crystalline/amorphous dual-phase high-entropy alloys with different amorphous layer spacing: (a) h =1 nm;(b) h =5 nm;(c) h =11 nm.(d) Atomic fraction evolution of FCC structure transformation to HCP structure with h=1,5 and 11 nm.

圖5(d)展示了三種典型的雙相HEAs 在拉伸過程中,相對于晶體的初相FCC 相轉變為HCP相的原子分數.從圖5(d)可以看出,針對于非晶厚度h=1 nm 的樣品和h=5 nm 的樣品,應變增加至0.035 和0.053 附近時FCC 結構到HCP 相的原子相變比例快速增加,而對于非晶厚度h=11 nm 的樣品,應變增加至0.065 附近時FCC 結構到HCP 相的原子相變比例才出現緩慢增加.對于非晶厚度h=1 nm 的樣品,應變增加至0.125后,FCC 結構到HCP 相的原子相變比例穩定在28%附近,隨后呈現快速的增加;對于非晶厚度h=5 nm 的樣品,隨著應變增加,FCC 結構到HCP 相的原子相變比例緩慢增加至22%附近;而對于非晶厚度h=11 nm 的樣品,FCC 結構到HCP 相的原子相變比例在應變0.125 之前穩定在2.0%附近,而在此應變之后緩慢的增加至16%.這與圖5(a)—(c)的結果是一致的.這是因為非晶相厚度的增加對應著晶體相尺寸的減小,并且隨著非晶相比例的增加,晶體相中的塑性變形會被非晶相進一步抑制.所以非晶相厚度適中時,雙相HEAs 主要通過晶體相的塑性變形(位錯滑移和FCC→HCP 相變)和非晶相的塑性變形(剪切轉變區域增殖和剪切帶的形成)共同主導.而非晶相厚度較大時,雙相HEAs 的塑性變形是非晶相中均勻剪切帶的形成主導的.

圖4 表明,非晶相的厚度對CoCrFeNiMn 雙相HEAs 的塑性變形機制有顯著影響,圖6 展示了不同非晶厚度的雙相HEAs 的非晶相中的塑性變形細節圖.由圖6 可知,非晶相厚度較小時,如h=1 nm 的模型(圖6(a)),雙相HEA 中非晶相原子的比例為12% (圖5(a)),由于非晶相厚度的限制,剪切轉變區域快速地增殖形成了較薄的剪切帶,所以在變形過程中對平均流動應力的貢獻很小.隨著h不斷增加,剪切轉變區域團簇增殖并形成剪切帶.例如h=5 nm 時,雙相HEA 中非晶相原子的比例為44% (圖5(b)),由于非晶相厚度適中,剪切帶胚胎周圍仍然有剪切轉變區域增殖,導致剪切帶的寬度變寬,非晶相中逐漸形成了與拉伸方向呈45°的分布均勻的成熟剪切帶,如圖6(b)所示.剪切帶形成過程中引發相對較穩定的塑性流動應力,這與圖2(a)粉色曲線幅度較小的波動相對應.這種與拉伸方向呈45°的剪切帶在其他金屬玻璃的變形過程中也被觀測到過[37,38].而對于非晶相厚度較大的雙相HEAs,如h=11 nm 的模型(圖6(c)),雙相HEA 中非晶相原子的比例為79% (圖5(c)),非晶相中大量的剪切轉變區域團簇在被激活和協同重排后形成了大而密集的剪切帶胚胎,且在拉伸作用下,這些剪切帶胚胎在非晶相中分布越發密集和均勻,因此該模型中非晶相的塑性承載能力最好,是雙相HEAs 中塑性變形的主要承載體.非晶相中形成較寬的剪切帶,所以在剪切帶形成過程中引發了穩定的塑性流動應力,這與圖2(a)紅色曲線幾乎穩定在某一特定值附近相對應.這就意味著,隨著非晶厚度的增加,非晶相對平均流動應力的貢獻逐漸增加.這與Zhou 等[25]的研究結果一致.綜上所述,在塑性變形過程中,非晶相通過剪切轉變區域不斷產生并形成剪切帶變形,非晶相厚度越大,非晶相中可以參與塑性變形的原子就越多,剪切帶的形成和增殖越容易、分布越均勻,同時晶體相中的塑性變形將慢慢退出主導地位.這也就意味著非晶相的加入可以降低雙相高熵合金中位錯發射的臨界應力,并且臨界應力隨著非晶相厚度增加而降低,這就解釋了圖2(c)中峰值應力隨著非晶相厚度的增加而逐漸降低的原因.

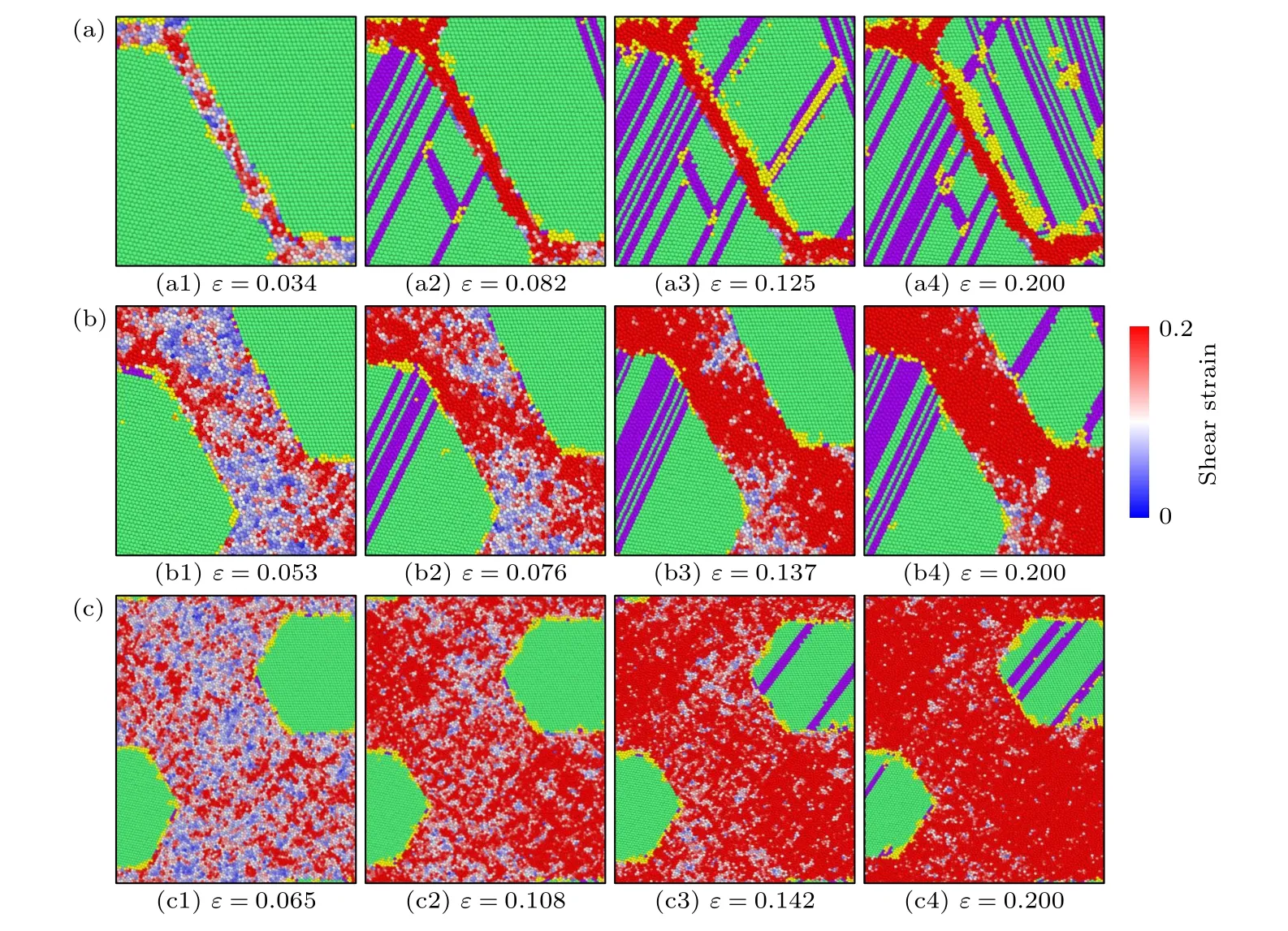
圖6 不同非晶厚度的雙相HEAs 中剪切帶的形成過程圖 (a) h =1 nm;(b) h =5 nm;(c) h =11 nmFig.6.Formation process of the shear band in CoCrFeNiMn crystalline/amorphous dual-phase high-entropy alloys with different amorphous layer spacing: (a) h =1 nm;(b) h =5 nm;(c) h =11 nm.

圖4(a)中提到非晶相厚度較小時,雙相高熵合金的變形主要是晶體相的塑性變形主導,為了詳細說明晶體相中的塑性變形細節,圖7 展示了圖4(a)中形變孿晶和Lomer-Cottrell 位錯鎖放大圖.圖4 中提及,應變為0.034 時雙相HEAs 的晶體相進入塑性階段,位錯滑移導致晶體相中形成了大量內稟層錯.隨著Shockley 部分位錯在{111}面上不斷滑移,內稟層錯轉變成外稟層錯(可以認為是厚度為一個原子層的孿晶胚胎).Shockley 部分位錯不斷滑移引發孿晶胚胎不斷長大,即孿晶的厚度逐漸生長為3—4 個原子層甚至更大,如圖7(a)所示,這與文獻[39,40]的結論是一致的.除了形成孿晶之外,Shockley 部分位錯的相互作用還會形成Lomer-Cottrell 位錯鎖,即兩個方向不同的堆垛層錯與晶格缺陷形成的V 型相互作用,如圖7(b)所示.前文提到,CoCrFeNiMn HEAs 的層錯能較低,這有利于其中位錯的分解.因此在變形過程中,在兩個不同的滑移面上存在高密度的分解位錯,即在和 (111) 平面上分別形成Burgers 矢量為(a/2[011])和的分解位錯(a是晶格常數),這兩種位錯發生如下反應:

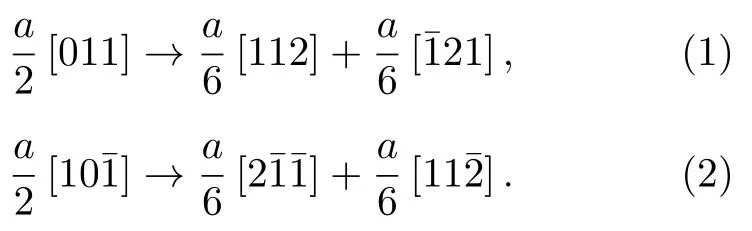
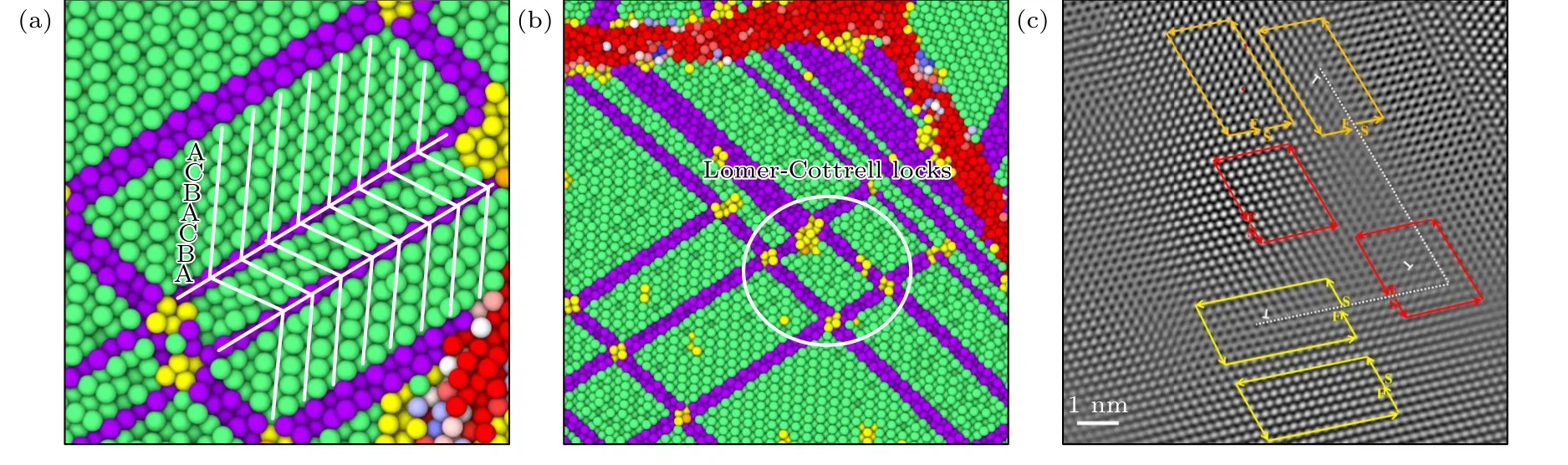
圖7 晶體相中的變形機理細節圖 (a) 形變孿晶細節圖;(b) 圖4(a3)中Lomer-Cottrell 位錯鎖的放大圖;(c) 實驗中觀察到的Shockley 部分位錯相互作用形成Lomer-Cottrell 位錯鎖[42]Fig.7.Details of the plastic deformation mechanism in crystalline structure: (a) Detail of the deformation twins;(b) zoomed up snapshot of the Lomer-Cottrell locks of Fig.4(a3);(c) the Lomer-Cottrell lock formed by the reaction of two Shockley partial dislocations in the experiment[42].

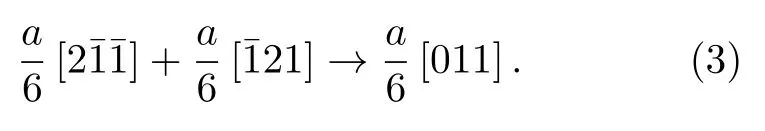
該梯桿位錯不在激活的{111}滑移面上,因此是不動的[39,41].位錯和大量的不動Lomer-Cottrell鎖導致了FCC 單相HEAs 的應變硬化,這也解釋了圖2(c)中厚度h=1 nm 的雙相HEA 的平均流動應力高于其他樣品.Jiang 等[42]研究FCC 結構Al0.1CoCrFeNi HEAs 的動態力學性能時也觀察到了這種Lomer-Cottrell 位錯鎖,他們不僅繪制了這些位錯的Burgers 回路,而且還繪制出了具有晶體學等效步驟的相應完美晶格,如圖7(c)所示,這和本文的結果是類似的.此外,Qi 等[39]在關于CoCr FeNiMn HEAs 的模擬中也觀察到了這種位錯鎖.這就從試驗和模擬的角度證明了我們結論的正確性.

圖8 為CoCrFeNiMn HEAs 中FCC 結構 向HCP 結構的相變機理圖.眾所周知,CoCrFeNiMn HEAs 具有FCC 晶體結構,如圖8(a)和圖8(c)所示.當材料進入塑性變形后,在拉伸載荷下Shockley部分位錯從晶粒界面處開始發射,并在{111}面上滑移,Shockley 部分位錯的運動使發生滑移的平面上的原子進行了重新定位,而相鄰的未滑移平面上的原子保持原有的位置不變,如圖8(a)和圖8(b)所示.隨著合金變形過程的進行,交替的滑移平面和未滑移平面的層數不斷增多[43],逐漸形成了HCP結構,如圖8(c)所示,即經過四次滑移之后,初始的FCC 密排結構ABCABCABCABC已經轉變為ABCABABABABC.相變之后FCC 和HCP 的晶體取向關系如下: (111)FCC//(0001)HCP和類似的相變結果在文獻[39,40]中也被觀測到.Fang 等[40]在研究同時包含FCC 結構和HCP 結構的CoCrFeMnNi HEA 力學性能時,指出HCP 結構HEA 是硬相而FCC 結構的HEA 是軟相,較軟的FCC 相體積分數增加,而較硬的HCP相體積分數降低時會導致HEA 材料整體的流動應力下降.這和本文的結論是一致的,即隨著非晶相厚度的增加,晶體相的比例在減小,因此塑性變形過程中HCP 相的比例也在減小,所以圖2(c)中平均流動應力的值隨著非晶相厚度的增加在減小.

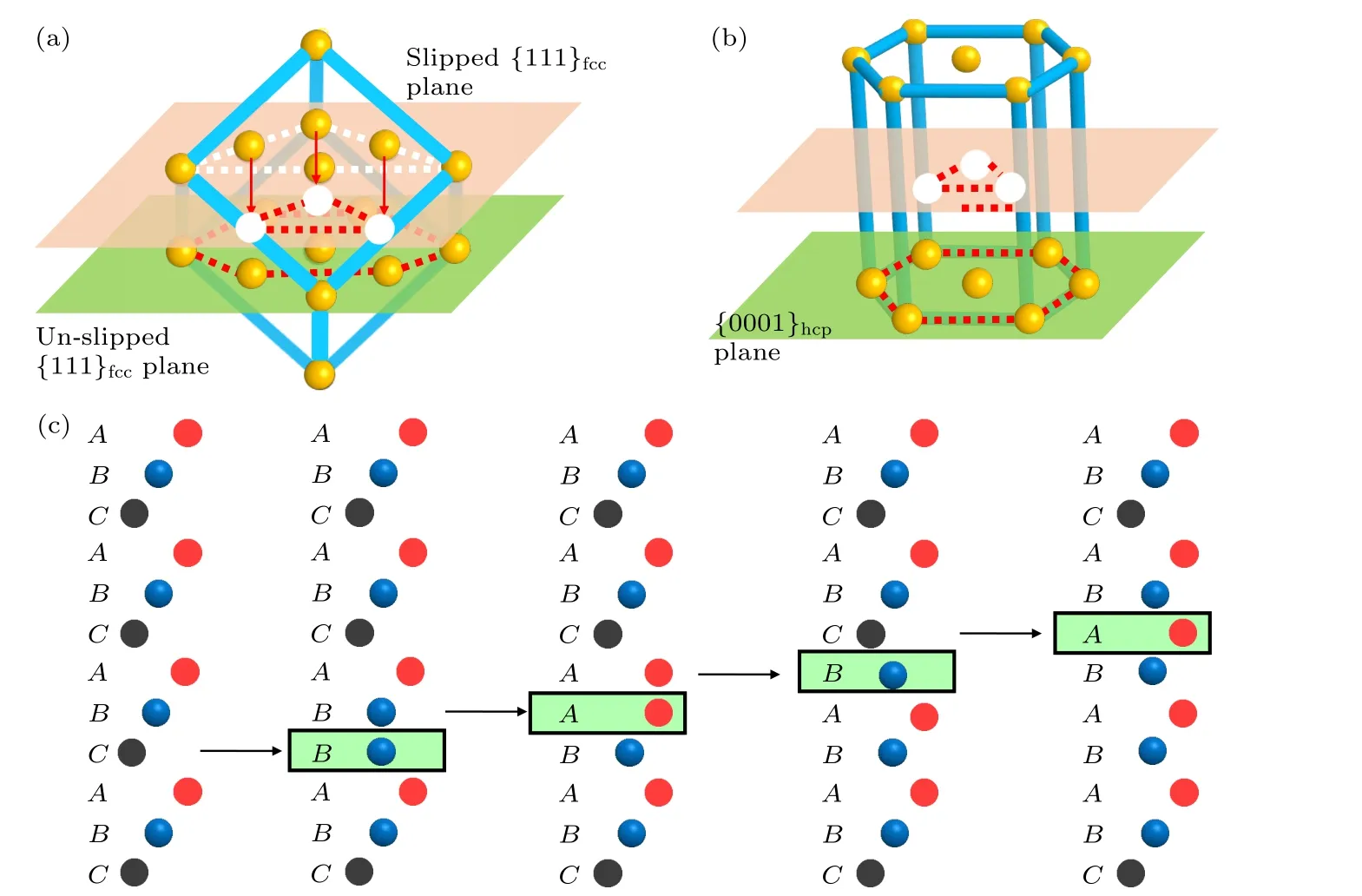
圖8 位錯滑移輔助下的FCC-HCP 轉變機制圖 (a) FCC 結構示意圖;(b) HCP 結構示意圖;(c) FCC→HCP 相變示意圖Fig.8.Schematic illustration of FCC-to-HCP transformation mechanism as assisted by dislocation glide: (a) Schematic illustration of FCC structure;(b) schematic illustration of HCP structure;(c) FCC-to-HCP transformation mechanism.

4 結論

本文采用分子動力學模擬的方法研究了組成相尺寸對CoCrFeNiMn 晶體/非晶雙相HEAs 的力學行為和塑性變形機制的影響.研究表明,CoCrFeNiMn 雙相HEAs 的塑性變形依賴于非晶相厚度.并且,隨著非晶相厚度的增加,楊氏模量、峰值應力以及平均流動應力均逐漸減小.非晶相厚度h=1 nm 的模型的表現出極好的力學性能,這歸因于晶體相在塑性變形過程中出現了孿晶、位錯鎖和FCC 結構到HCP 結構的相變.非晶相厚度較小時,CoCrFeNiMn 雙相HEAs 塑性變形主要由晶體相中的位錯滑移及其引發的FCC→HCP相變的轉變主導;非晶相厚度適中時,CoCrFeNiMn雙相HEAs 主要通過晶體相中的位錯滑移、FCC相到HCP 相的轉變和非晶相的剪切帶增殖等進行塑性變形;非晶相厚度較大時,雙相高熵合金的塑性變形由非晶相中均勻剪切帶的形成主導.本文的研究結果對于設計同時兼顧高強度和高韌性的高熵合金材料和推動其應用有一定的指導作用.