擴張狀態觀測器下的FFSR末端軌跡跟蹤控制

陳志華，胡安正

（1.襄陽汽車職業技術學院，湖北 襄陽 441021；2.湖北文理學院物理與電子工程學院，湖北 襄陽 441053）

1 引言

空間機器人，作為一種智能操作系統，能夠高效地執行航天探測、在軌維修、空間建造等諸多任務，從而把航天員從復雜的太空環境中解放出來，近年來發展迅速且得到了航天人員以及控制領域專家學者的廣泛關注[1?3]。根據基座的控制方式的不同，空間機器人的控制可分為基座位置受控、基座姿態受控、基座位姿受控和自由漂浮四種模式[4]。根據控制空間的不同，空間機器人的控制又可分為關節空間控制即通過對關節角的控制實現軌跡跟蹤，以及任務空間控制即直接對機械臂末端控制以實現機械臂抓手的軌跡跟蹤[5]。自由漂浮空間機器人（Free Floating Space Robot，FFSR）任務空間軌跡跟蹤控制由于具備無需額外負載燃料、姿態靈活可調整、直接控制末端更符合實際工程需求等優點，逐步發展成為空間機器人控制領域研究重點。文獻[6]針對模型參數不精確條件下的FFSR任務空間軌跡跟蹤控制問題，提出了一種逆鏈逼近的自適應控制方法，實現了機械臂末端軌跡的精確跟蹤控制；文獻[7]考慮FFSR的模型誤差，提出一種基于SDRE的末端軌跡跟蹤控制方法，在實現了末端軌跡精確跟蹤的同時考慮了輸出力矩的優化；文獻[8]利用神經網絡的逼近特性和自適應控制器的學習特性，提出了一種自適應神經網絡控制方法，實現了FF?SR的末端軌跡跟蹤；文獻[9]基于拉蓋爾模型提出了一種離散模型預測控制方法，實現了FFSR末端的位置和速度跟蹤。

在上述文獻的研究中，均較好的實現了FFSR的任務空間軌跡跟蹤控制，且考慮了模型參數以及外部干擾等復雜因素，但在控制系統設計上均需實時測量關節角和末端的位置信息以及速度信息，而空間機器人多處于低速運動狀態、空間環境噪聲大，速度測量易出現較大誤差，且測速系統將增加系統質量和運行成本，引入觀測器是一種較好解決方案。

文獻[10]針對控制力矩受限條件下的空間機械臂軌跡跟蹤控制問題，采用速度濾波器對速度信號進行估計，提出了一種自適應控制方法；文獻[11]采用神經網絡觀測器對系統速度信息進行估計，提出了一種神經網絡自適應魯棒控制方法；文獻[12]基于自抗擾技術，設計了擴張狀態觀測器，并結合模糊控制實現了機械臂的軌跡跟蹤控制。文獻[10?12]雖然解決了測速問題，但其主要針對空間機器人關節空間軌跡跟蹤控制，而對于FFSR系統，由于基座位置易受反作用力運動，因此即便實現了關節角的精確跟蹤，仍會由于基座位姿的改變使末端軌跡跟蹤產生誤差。

綜合考慮上述問題，針對存在模型參數不精確以及外部擾動等不確定性條件下的FFSR末端軌跡跟蹤控制問題，提出一種基于擴張狀態觀測器的優化控制方法。

首先，在建立FFSR 關節空間動力學和運動學模型的基礎上，采用增廣向量法獲得FFSR的偽線性狀態空間方程；而后，設計擴張觀測器對狀態變量以及系統不確定項進行在線估計，并采用Lyapunov方法對所設計觀測器的穩定性進行分析；進而，將觀測器的輸出作為控制器的輸入，提出一種基于SDRE的優化控制方法，實現FFSR系統末端軌跡的精確跟蹤控制。數值仿真證明了所提控制方法的有效性。

2 FFSR系統建模

不失一般性，單臂空間機器人通常由基座B0以及搭載在其上的若干連桿機械臂Bn以及末端抓手組成H0，機械臂與基座有且僅有一個連接點J1，如圖1所示。

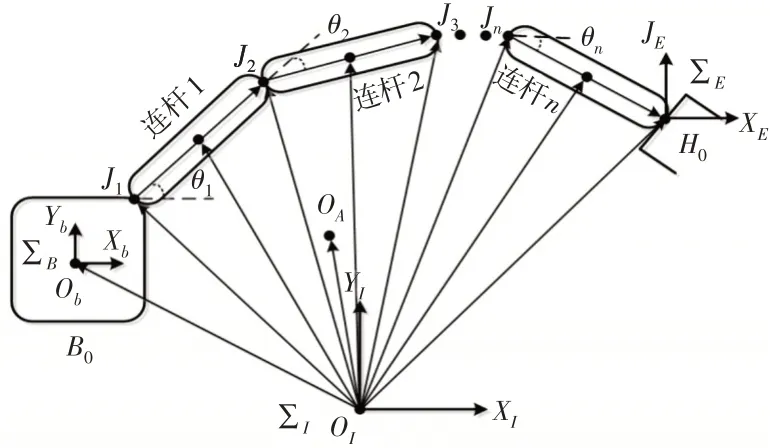
圖1 單臂空間機器人系統結構圖Fig.1 FFSR Structure Diagram

3 控制系統設計

在不測量角速度以及位置速度信息條件下，為實現FFSR系統末端軌跡精確跟蹤控制，設計控制系統結構，如圖2所示。

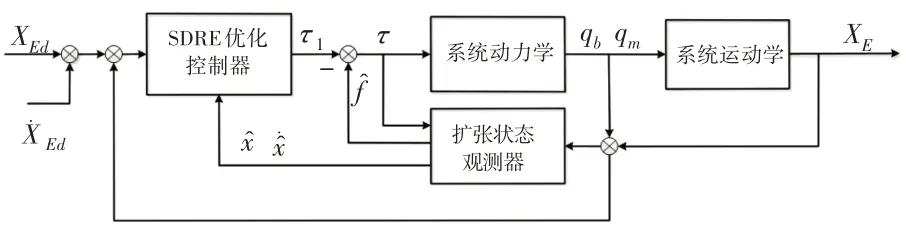
圖2 控制系統結構Fig.2 Control System Structure

從圖中可以看出控制系統設計的基本原理為：首先以角度和末端位置信息為輸入，設計擴張狀態觀測器，對狀態變量以及不確定項進行在線估計；進而，將觀測器的輸出作為控制器的輸入，提出一種基于SDRE的優化控制方法，并將觀測器獲得的干擾觀測量反饋至控制器中，獲得最終控制律。

3.1 擴張狀態觀測器設計

為便于狀態觀測器的設計，需將式（5）所示的關節空間模型轉變為狀態空間模型。

根據式（4）可得：

定義增廣狀態變量x=[x1x2]T=[q?m XE]T，輸出變量y=XE，由式（5）、式（6）可得：

式中：x?1、x?2、f?——狀態觀測以及誤差觀測向量；α1、α2、α3—正實數；ε>0；且多項式s3+α1s2+α2s+α3滿足Hurwitz條件。

3.2 擴張狀態觀測器穩定性分析

為證明所設計的擴張狀態觀測器式（8）能夠實現對狀態變量以及誤差變量的在線估計，即：當t→∞時，x?1→x1、x?2→x2、f?→f。定義：

3.3 控制器設計

擴張狀態觀測器重點解決的是控制系統狀態變量以及擾動變量的在線觀測問題，為實現FFSR系統末端的軌跡跟蹤控制，進一步針對式（7）所示的增廣狀態空間模型，將觀測器的輸出作為控制器的輸入，提出一種基于SDRE的優化控制方法。

首先，不考慮系統模型不精確以及外部擾動帶來的不確定性，則式（7）轉化為：

定義FFSR系統期望末端軌跡為yd(t)，實際軌跡為y(t)，軌跡跟蹤誤差為e=yd(t)?y(t)，則按SDRE 控制原理[15]，針對形式如式（15）所示的狀態空間模型，進一步結合狀態觀測器的觀測結果，可設計控制器以及性能評價指標分別如下所示：

4 仿真實例

為驗證所提控制方法的有效性，以文獻[7]中的兩連桿FFSR為例，進行Matlab∕Simulink數值仿真，空間機器人各項參數，如表1所示。

表1 系統參考慣性參數Tab.1 Inertial Parameters of System

表2 系統真實慣性參數Tab.2 Inertial Parameters of System

外部干擾為：τd=0.2+e+1.5e?（單位：N ?m，e=yd(t)?y(t)為跟蹤誤差）。設置仿真時長t=20.0s，仿真結果，如圖3～圖7所示。其中。FFSR系統末端軌跡跟蹤情況。直接反應了所設計的控制器的控制效果，如圖3所示。FFSR機械臂兩個關節的輸出力矩，反應了控制器輸出力矩優化情況，如圖4所示。擴張狀態觀測器分別對狀態變量x1、x2以及系統不確定項f的觀測范數值與實際范數值的跟蹤情況，直接反應了擴張狀態觀測器的穩定性以及有效性，如圖5～圖7所示。

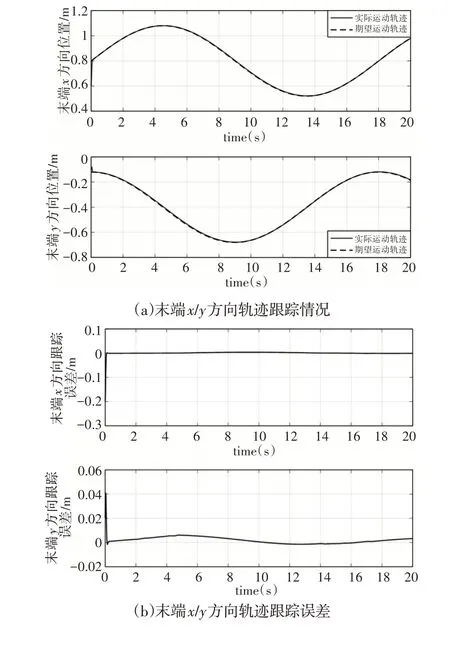
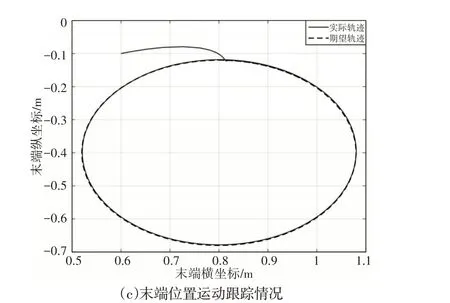
圖3 末端軌跡跟蹤情況Fig.3 End Track Tracking

在所設計的控制器作用下，FFSR機械臂末端軌跡跟蹤情況，如圖3所示為。其中，機械臂末端軌跡的x、y方向分量跟情況，如圖3（a）、圖3（b）所示。從仿真結果可以看出，期望軌跡xd為正弦運動函數、yd為余弦運動函數，在控制器作用下，實際運動分量與期望分量基本保持一致，跟蹤誤差均控制在0.01以內；機械臂末端在慣性坐標系下運動軌跡的直接反映，從仿真結果可以看出，期望運動軌跡為一橢圓，在控制器作用下，末端抓手迅速從初始軌跡點運動到指定點，且后續始終沿期望軌跡運動，如圖3（c）所示。控制器輸出力矩，如圖4所示。從仿真結果可以看出，不僅考慮了控制器控制效果，即使機械臂末端實現精確軌跡跟蹤，且同時考慮了控制器輸出力矩的大小，所設計的控制器除初始力矩稍大外，整個控制過程輸出力矩均較小，實現了能量的優化。

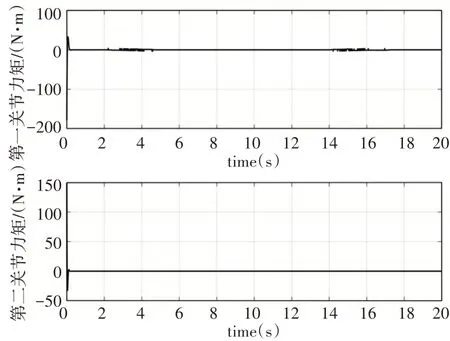
圖4 關節控制力矩Fig.4 Joint Control Torque

設計擴張狀態觀測器的觀測情況，如圖5～圖7所示。

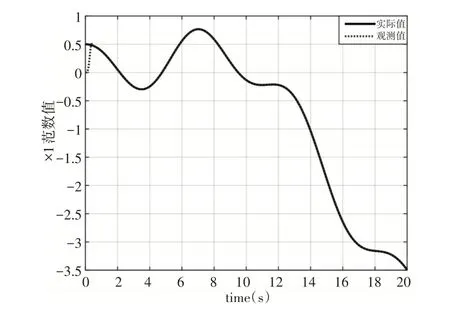
圖5 狀態變量x1觀測情況Fig.5 Observation of State Variable x1

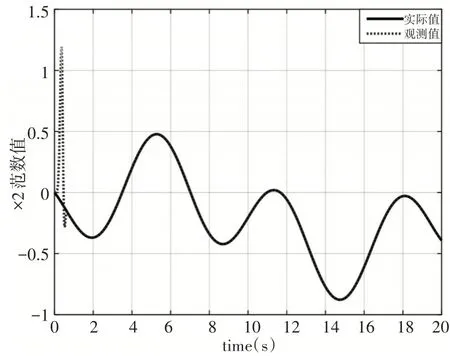
圖6 狀態變量x2觀測情況Fig.6 Observation of State Variable x2

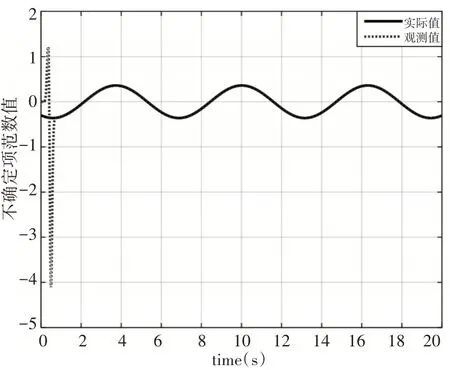
圖7 不確定項觀測情況Fig.7 Observation of Uncertainty

從仿真結果可以看出，所設計的擴張狀態觀測器能夠較好的對系統狀態變量以及系統不確定項的在線觀測，即實現x?1→x1、x?2→x2、f?→f。

5 結論

傳統的空間機器人控制方法往往需實時測量關節角速度和末端的位置信息，而空間機器人多處于低速運動狀態、空間環境噪聲大，速度測量易出現較大誤差，且測速系統將增加系統質量和運行成本。重點針對這一問題，同時考慮輸出力矩的優化，提出了一種基于擴張狀態觀測器的優化控制方法，實現了末端抓手的精確軌跡跟蹤控制。所提方法在以下幾個方面具有一定優越性：（1）實現了對FFSR系統末端抓手的直接控制，較傳統關節空間控制更具工程應用價值；（2）通過設計擴張狀態觀測器實現了對擴張狀態空間方程的狀態變量以及系統不確定項的在線觀測，從而無需測量關節角速度以及末端位置信息；（3）基于SDRE控制原理提出的優化控制方法實現了能量的優化，控制力矩保持在較小范圍。