考慮不平衡力與擾動力的深溝球軸承動力學模型

歐旭鵬，張義民，張 凱，王一冰

（沈陽化工大學裝備可靠性研究所，遼寧 沈陽 110142）

1 前言

滾動軸承作為旋轉機械的一個重要組成部分，對整個系統的運行起著決定性的作用。為了更加準確了解軸承的運行狀態，通常建立滾動軸承動力學模型。動力學模型不但可以分析軸承的載荷和轉速隨時間變化的工作狀態，并且可以更好的描述軸承動態響應特征。建立準確地動力學模型，可以進一步了解軸承在運行過程中的接觸振動機理[1]。

最早，文獻[2]考慮了軸系和支承結構的彈性變形，提出了故障軸承擬靜力學分析方法；文獻[3]對實際潤滑的球型分離器和球的運動進行了全面的綜合分析。文獻[4]對軸承運轉過程中的振動進行研究。研究表明了，軸承運行噪聲和不穩定運行的最根本原因是變柔度振動；文獻[5]提出了新的動力學模型，模型中考慮了軸承各元件尺寸變化、滾道曲率等因素；文獻[6]考慮了軸承裝配誤差以及徑向間隙的影響，分析了轉速變化對軸承振動的關系；文獻[7]以Hertzian接觸變形理論為基礎，建立了2自由度缺陷動力學模型，來模擬內、外圈單點缺陷，研究了局部故障下的動態特性；文獻[8]建立了深溝球軸承內圈和外圈表面局部故障的2自由度動力學模型，分別得到了內、外圈表面單故障的深溝球軸承的振動響應；文獻[9]考慮了表面粗糙度對滾道缺陷的徑向加載雙列軸承準靜態載荷分布和剛度的影響，建立了2自由度的動力模型。

以上研究學者們從不同研究方向建立動力學模型。然而，不平衡力與擾動力對軸承的影響在動力學模型中卻鮮見研究，為了更加準確地揭示振動響應的機理，考慮了軸承受到不平衡力與運行產生的擾動力的影響，并且在建立模型時考慮了軸承產生共振部分，建立軸系?內圈?外圈?軸承座四自由度傳遞深溝球軸承振動的解析模型。

對深溝球SKF6205 ?RS為研究對象建立模型，采用四階變步長的Runge ?Kutta法對動力學方程式進行求解，得到了振動響應時域信號以及頻域信號，并對結果進行了細化傅里葉處理，最后與西儲大學軸承實驗結果進行了比較，驗證了模型的正確性和可靠性。

2 深溝球軸承動力學模型的建立

2.1 簡化模型

深溝球軸承非線性動力學模型簡圖，如圖1 所示。基于Hertzian接觸理論，建立滾動軸承動力學模型。在建立模型時，進行如下假設：滾動體是等距均勻分布在內圈且進行純滾動運動；不考慮潤滑、油膜作用；忽略滾動體慣性效應、陀螺運動以及熱效應引起的零件變形的影響等。

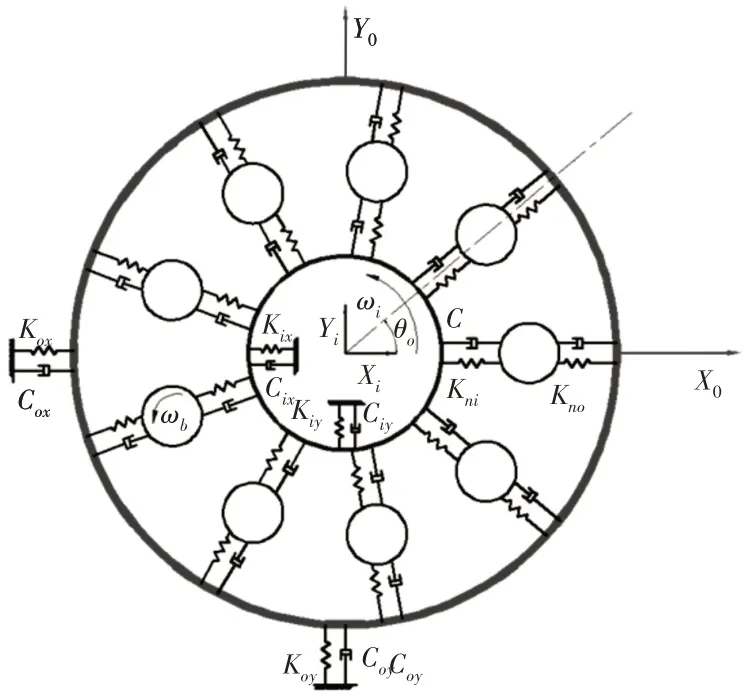
圖1 深溝球軸承模型簡化Fig.1 Simplified Model of Deep Groove Ball Bearing

2.2 接觸剛度

Hertzian總接觸剛度kn，是由滾道的接觸幾何形狀決定的，總載荷—位移等效系數由滾動體與內圈和外圈的接觸等效剛度kni，kno綜合求得［10］。

2.3 徑向變形

設x軸正方向與x軸正方向上方θio(t)的第一個滾珠夾角為θo，第i個滾子經過t時間后轉過的角度為θi，即：

式中：x(t)、y(t)—內外圈的相對位移量；

Cr—徑向間隙。

2.4 Hertzian接觸力

軸承的內外圈滾道與球滾動體之間的接觸形式為點接觸。根據Hertzian接觸理論，非線性載荷?位移關系為：

式中：Hi(t)—判斷滾動體與滾道是否接觸的參數。

如今，駕駛人也可跨省繳納交通罰款啦。除了營業網點外，還可以通過手機銀行等線上渠道付款。符合條件的，當事人還可以委托他人代處理。

2.5 阻尼力

對阻尼采用不同的計算方法：軸承接觸阻尼的主要來源是滾動軸承與內外滾道之間存在的潤滑膜，第i個滾子的接觸阻尼力可以表示為：

2.6 不平衡力

軸承運行時的不平衡力受力分析，如圖2所示。

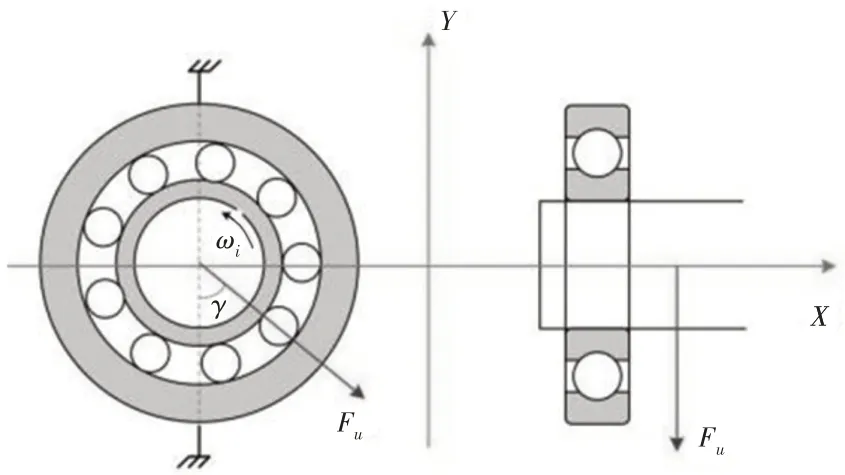
圖2 不平衡力受力分析Fig.2 Force Analysis of Unbalanced Force

滾動軸承受到轉軸不平衡力將產生受迫振動，其振動頻率為轉軸的旋轉頻率，產生的不平衡力為：

2.7 擾動力

在軸承運行時，由于承載滾子數在變化，導致內圈會受到軸系產生較小的擾動力，擾動力為：

式中：Nc—承載滾子數（不是總滾子數）；

F—細小擾動力；

ωb—滾子自轉角速度。

3 動力學方程的建立

根據前面簡化的軸承系統模型，在建立模型時，考慮了不平衡力以及擾動力，以及軸系—內圈，外圈—軸承座的非線性耦合關系。以X軸、Y軸為橫縱坐標，軸承內外圈在4個方向建立了4自由度的動力學方程，如式（12）所示。

式中：mi—軸承內圈及軸系的等效質量；

mo—軸承外圈的等效質量；

kox、koy—軸承與軸承座之間的支撐剛度；

kix、kiy—軸承軸系之間的剛度；

cox、coy—軸承軸承座之間的支撐阻尼；

cix、ciy—軸承與軸系之間的阻尼。

4 數值計算及實驗驗證

4.1 數值模擬

對SKF6205?RS深溝球軸承為研究對象進行模擬驗證。采用4階Runge?Kutta對式（12）進行求解，獲得深溝球軸承的振動響應結果。其中步長為1∕12000s，位移初始值為1×10?6m，速度初始值為0m∕s，外載荷為Wx=550N，Wy=650N，SKF6025?RS 軸承參數以及運行參數，如表1所示。

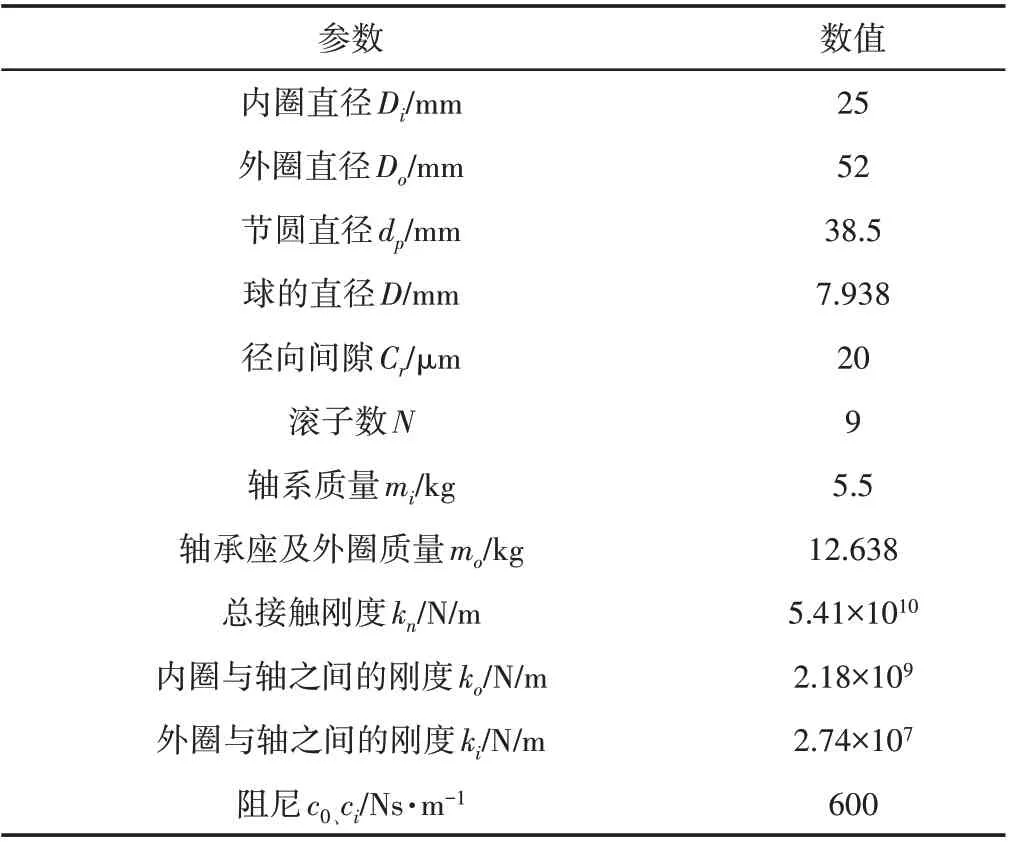
表1 SKF6025-RS軸承參數以及運行參數Tab.1 SKF6025-RS Bearing Parameters and Operating Parameters

動力學方程模擬得到的時域圖，如圖3（a）所示。由于初值原因在前期有一定幅值的沖擊；時域信號快速傅里葉變化得到的頻域圖，如圖3（b）所示。可以看出共振頻率分別為1065Hz，2102Hz，（0～350）Hz的細化傅里葉變化得到的頻譜圖，如圖3（c）所示。

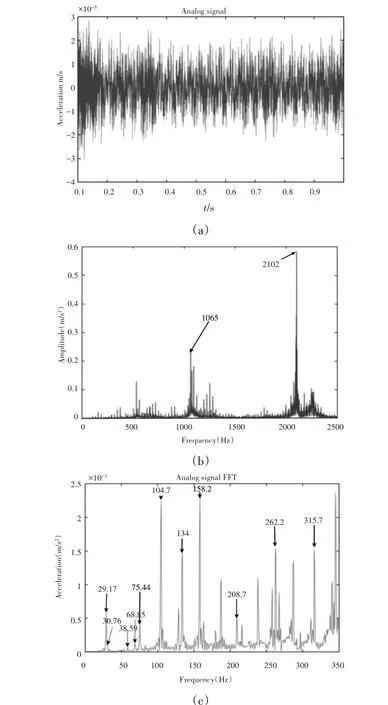
圖3 數值模擬結果Fig.3 Numerical Simulation Results

其中，29.17Hz 為轉軸頻率，58.59Hz 為二倍轉頻頻率，104.7Hz 為滾動體通過外圈的頻率，208.7Hz 為二倍頻；158.2Hz為滾動體通過內圈的頻率，315.7Hz為二倍頻；262.2Hz為滾動體通過外圈頻率和通過內圈頻率之和，30.75Hz為轉軸不平衡力激勵的轉頻，68.85Hz為細小擾動力激勵的頻率。

4.2 實驗及結果分析

試驗軸承選取了SKF6205 ?2RS深溝球軸承，試驗采樣頻率為12kHz。軸承詳細參數，如表1所示。轉速在1750rpm下的時域圖，由于運行環境、軸承自身運行中噪聲以及其它力的影響，時域信號中有輕微沖擊，如圖4（a）所示。該轉速下的頻域圖，如圖4（b）所示。由于滾動軸承的通過頻率都在低頻段，中頻段反應出軸承或結構零件的共振頻率成分，因此選取了中、低頻段，在圖4（b）中，中頻段（1～2.5）kHz 中有兩個明顯突起，分別是1065Hz、2102Hz，這與數值模擬傅里葉變化以后的圖4（b）中1065Hz 和2100Hz左右的凸起很接近，這說明了本文的模型在考慮共振部分的因素是很有必要的。對（0～350）Hz采用細化FFT，細化FFT以后的頻譜圖，如圖4（c）所示。從圖中可以看出幾個重要的旋轉頻率和通過頻率，不平衡力激勵頻率為30.03Hz，與仿真結果是相一致的，68.12Hz為擾動力激勵頻率，與仿真結果是一致的，外圈通過頻率為104.6Hz，內圈通過頻率157.1Hz 等，希爾伯特調解圖，如圖4（d）所示。

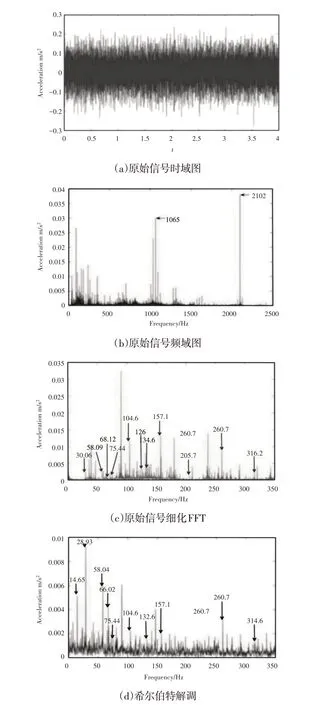
圖4 轉速1750rpm的實驗結果Fig.4 Experimental Results with a Rotation Speed of 1750rpm

經過對振動信號希爾伯特解調以后，可以清晰地觀察到軸承運行過程中的旋轉頻率和通過頻率。轉頻為28.93Hz，跟理論值29.11Hz有點誤差，這是由于轉軸產生的不平衡力的原因；58.09Hz為二倍頻，與理論值58.33Hz是基本吻合的；圖中，1∕2fi為14.65Hz，這是軸回振動，可能是由于潤滑不良引起的。

4.3 共振帶頻域分析

在建立模型時，考慮了中頻段的共振因素。將模擬結果與試驗結果結合分析。模型中其他參數不變，（1）改變Hertzian 接觸剛度kn的值，代入系統模型方程中，kn= 3.0 × 1010，kn= 6.0 ×1010的頻域圖，如圖5（a）、圖5（b）所示。

結果發現改變kn時，1065Hz左右的共振頻率，會發生變化，這就說明實驗中1065Hz處的共振頻率就是由軸承內部的剛度引起的；（2）改變軸承與軸承座之間的剛度kox的值，kox= 9 × 108的頻域圖，如圖5（c）、圖5（d）所示。

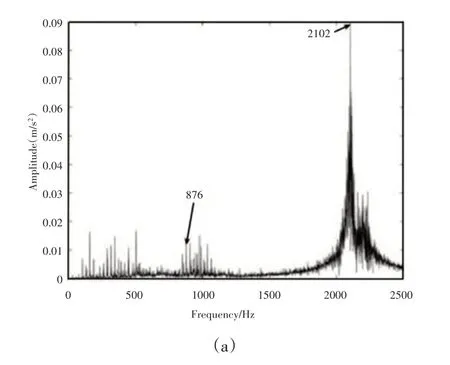
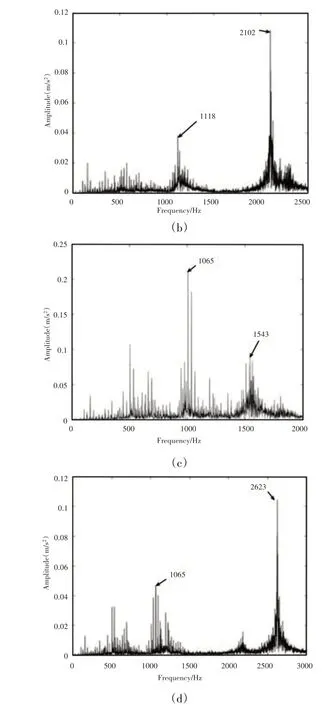
圖5 改變參數的頻域圖Fig.5 Frequency Domain Diagram of Changing Parameters

2102Hz 左右的共振頻率，會發生變化，說明實驗中的2102Hz處的共振是由軸承與軸承座之間的剛度引起的共振。上述研究結果表明，提出的模型的主要貢獻是獲得的加速度頻譜與實驗測量所得的加速度頻譜基本相一致。

模型真實模擬軸承共振現象，且模擬與試驗頻譜中的共振頻率是一致的。結果證明，在一定的誤差范圍之內，提出的模型具有正確性和準確性的。

5 結論

本研究考慮了內圈受到軸系不平衡力以及擾動力的影響，建立4自由度深溝球軸承動力學模型。通過所建模型及實驗對比結果表明，不平衡力及擾動力激勵頻率相一致，中頻段的共振頻率也是相一致的。通過定量分析得到試驗中頻段頻率1065Hz是由Hertzian接觸剛度引起的，2102Hz是由軸承外圈與軸承座的支撐剛度引起的。通過數值模型仿真與實驗測試結果對比，結果吻合度較好，說明該模型的準確性和可靠性較好。