電纜硅橡膠附件溫度和熱老化對接頭界面壓力的影響

杜光旭，方春華，夏 榮，丁 璨，吳 田

（1. 三峽大學 電氣與新能源學院，湖北 宜昌 443002；2. 中國電力科學研究院有限公司，湖北 武漢 430074）

0 引言

電纜接頭是電纜事故發生的薄弱環節，電纜附件與交聯聚乙烯界面壓力不足是引發接頭絕緣擊穿故障的重要原因之一。已有研究表明，電纜附件與主絕緣界面壓力在0.10～0.25 MPa 時，能夠滿足電氣強度的要求[1-2]。電纜線芯發熱會導致附件絕緣材料溫度升高，影響附件硅橡膠材料的力學性能，同時附件長時間在高溫下運行會導致附件硅橡膠老化，力學性能出現衰退[3-4]。因此，研究電纜附件溫升和老化后的界面壓力具有重要意義。

目前，國內外對電纜附件界面壓力影響因素開展了許多研究。柳松等[5]對電纜附件的過盈配合進行ANSYS 仿真，研究了過盈量、厚度和面壓的關系；謝強等[6]通過建立電纜接頭仿真模型，研究了橡膠本構模型和附件結構對接頭界面壓力的影響；包淑珍等[7]研究了退役電纜絕緣層在變溫環境中的彈性模量與界面壓力的關系，但附件在變溫和老化環境中的力學性能缺少研究；柳松等[8]通過測量不同溫度下附件的彈性模量計算界面壓力，但該方法存在一定誤差，采用橡膠本構模型計算界面壓力更能體現材料的非線性力學性能。魯中亞等[9]研究了預制型電纜終端應力錐在變溫環境下的應力應變關系，擬合出Mooney-Rivlin 本構模型參數，但沒有對高溫環境中的界面壓力變化進行研究。

綜上所述，現有研究主要集中在電纜附件常溫環境下的界面壓力，缺乏高溫環境下和老化后附件硅橡膠材料的拉伸應力應變數據和本構模型參數，對變溫環境中電纜接頭界面壓力變化的研究也較少。為此，本文以10 kV 冷縮電纜中間接頭為例，采用單軸拉伸試驗測定附件硅橡膠材料在高溫環境和不同熱老化時長后的應力應變數據，根據試驗數據擬合硅橡膠的超彈性Yeoh本構模型，建立簡化的中間接頭二維軸對稱有限元模型，利用仿真分析溫度及熱老化對附件硅橡膠界面壓力的影響。

1 電纜接頭附件拉伸試驗

1.1 試驗制作及試驗工況

按照HG/T 2645—2011《橡膠專用裁刀技術條件》，將高溫硫化形成的半導電硅橡膠和絕緣硅橡膠裁剪成啞鈴Ⅱ型試樣，如圖1 所示。試樣的窄部分平均寬度為4 mm，平均厚度為2 mm，試樣標距為25 mm，試樣平均長度為75 mm。

圖1 啞鈴型硅橡膠試樣Fig.1 Dumbbell-shaped silicone rubber specimens

由于三芯電纜附件外部是由鎧裝帶繞包而成，接頭內部環境密閉，對流換熱系數小，導致附件外表面和內表面溫差小于7℃[10]，故本文在計算界面壓力時認為附件各處溫度相等。為了提高試驗準確性，模擬電纜附件所處環境溫度，硅橡膠試樣在常溫25℃，高溫50、75、100℃進行拉伸試驗，每組拉伸試驗重復3次。

按照GB/T 3512—2001，采用上海一恒科學儀器有限公司生產的DHG-9425A 型鼓風干燥箱在130、150、170℃對試樣進行加速熱老化試驗。因為10 kV 電纜接頭產生的位移形變為1～2 mm，附件厚度為10～20 mm，位移變形約為附件厚度的10%，所以老化時將啞鈴型試樣預拉伸10%。老化完成后，取出試樣，室溫下放置30 min 后進行拉伸。依據GB/T 528—2009[11]，采用馥勒儀器科技有限公司生產的FL-GD 型拉伸試驗機進行單軸拉伸試驗，拉伸速率為500 mm/min。

1.2 拉伸應力應變曲線

圖2、圖3分別為附件絕緣硅橡膠和半導電硅橡膠在不同溫度下的應力應變曲線。從圖2～3 可以看出，絕緣硅橡膠和半導電硅橡膠的力學性能受溫度影響較大，對溫度比較敏感。在相同伸長率下，兩種材料在常溫25℃時的應力最小，隨著溫度升高，絕緣硅橡膠和半導電硅橡膠的拉伸應力呈先增大后減小的趨勢，在75℃時拉伸應力最大。附件硅橡膠拉伸變形時，分子鏈變成伸展狀態，有序度增加，熵變小，由于分子熱運動，分子會自發地恢復到原來狀態，使熵增大，由此產生彈性恢復力。當溫度升高時，使熵恢復趨勢更加強烈，因此溫度升高，彈性模量會隨之增加。當溫度高于75℃，考慮到熱效應和體積膨脹，同時溫度過高使有效交聯密度降低，導致分子間作用和鏈段間作用削弱，應力會減小。

圖2 不同溫度下絕緣硅橡膠的應力應變曲線Fig.2 Stress-strain curves of insulating silicone rubber under different temperatures

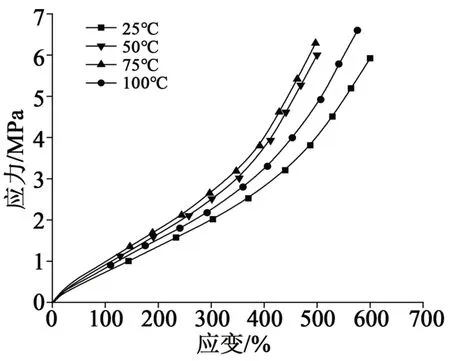
圖3 不同溫度下半導電硅橡膠的應力應變曲線Fig.3 Stress-strain curves of semi-conductive silicone rubber under different temperatures

由于在130、150、170℃熱老化條件下硅橡膠的應力應變曲線變化趨勢相同，只列出絕緣硅橡膠和半導電硅橡膠在130℃熱老化48、96、144、192、360、528、720 h 時測量得到的應力應變曲線，結果如圖4～5所示。由圖4～5可以看出，隨老化時間的增加，在相同伸長率下，拉伸應力不斷下降，力學性能降低。兩種材料的應力應變響應均為非線性彈性特征，隨著材料溫度升高和老化時間增加，這種非線性特征的趨勢沒有發生改變。

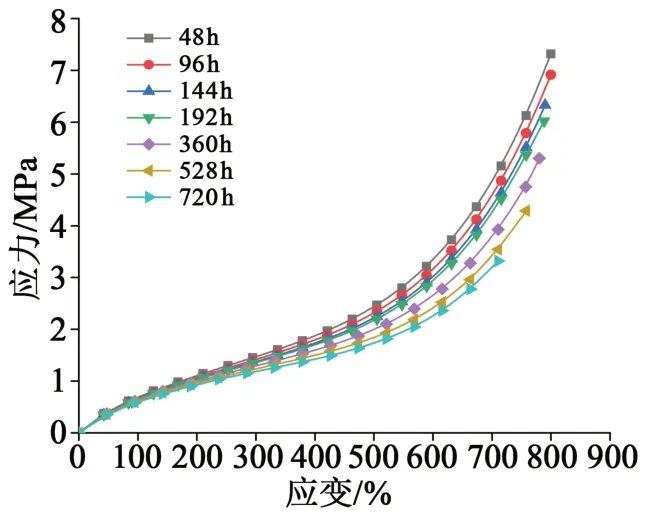
圖4 130℃不同老化時長絕緣硅橡膠的老化應力應變曲線Fig.4 Stress-strain curves of insulating silicone rubber after ageing for different time at 130℃

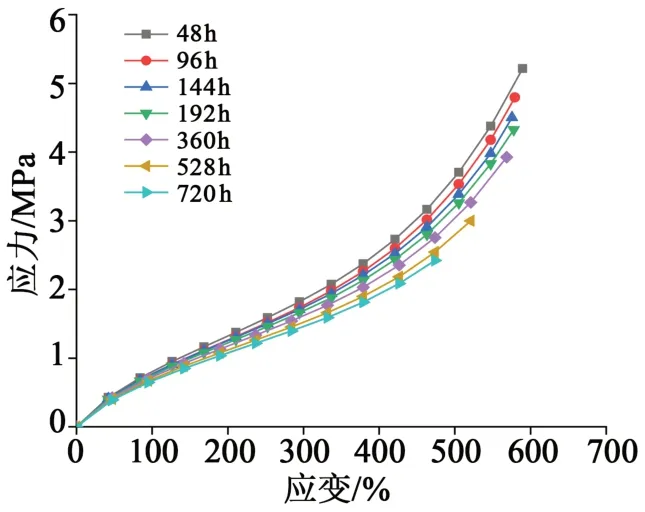
圖5 130℃不同老化時長半導電硅橡膠的應力應變曲線Fig.5 Stress-strain curves of semi-conductive silicone rubber after ageing for different time at 130℃

2 界面壓力仿真分析

2.1 仿真模型

以10 kV 冷縮型電纜中間接頭為研究對象，建立二維軸對稱接頭模型，其仿真模型結構如圖6 所示。為減少計算量，簡化后的電纜接頭模型由銅芯、交聯聚乙烯、應力錐、高壓屏蔽管、電纜附件絕緣、絕緣膠帶、壓接管組成。應力錐和高壓屏蔽管由半導電硅橡膠組成，附件絕緣由絕緣硅橡膠組成。應力錐、高壓屏蔽管和絕緣橡膠通過高溫硫化成附件整體。電纜冷縮附件與電纜主絕緣XLPE 冷裝配，形成不同介質復合界面，附件硅橡膠以一定的過盈量壓縮變形在復合界面產生壓力。

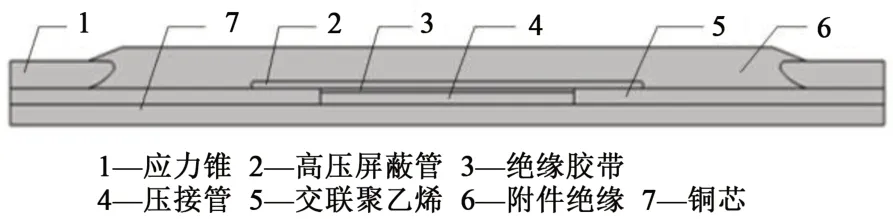
圖6 10 kV電纜接頭仿真模型結構示意Fig.6 Schematic structure of 10 kV cable joint simulation model

在有限元仿真分析中，采用罰函數分析方法來解決硅橡膠的幾何非線性問題。當兩個邊界相互擠壓時，在兩接觸面的各節點間建立一個虛擬單元模擬面與面接觸。對模型定義裝配體，創建接觸對，設置硅橡膠為接觸體，交聯聚乙烯為目標體，接觸表面從幾何目標表面偏移的量即為過盈量。模型兩端邊界設置為輥支承約束條件。在二維模型網格劃分中，研究的是硅橡膠在過盈面的變形及受力，故硅橡膠劃分較細，交聯聚乙烯及銅芯模型中網格較少。電纜中間接頭附件的硅橡膠材料在壓縮變形過程中體積變化很小，通常被視為近似不可壓縮和各向同性的超彈性材料，變化過程復雜且高度非線性，因此本文基于橡膠超彈性Yeoh 本構模型，利用與材料應變能偏量部分有關的3個材料參數C10、C20和C30來計算界面壓力。

2.2 應力-應變關系確定硅橡膠本構模型

Yeoh 本構模型的彈性應變能函數關系如式（1）所示[12]。

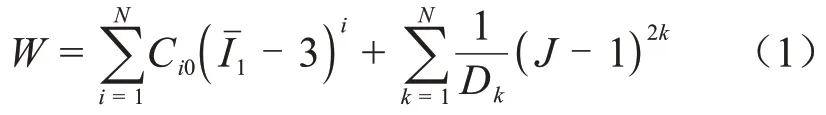
式（1）中：J為硅橡膠變形前后的體積比；Iˉ1為第一應變張量不變量；N、Ci0和Dk為輸入參數。由于硅橡膠近似為不可壓縮材料，取J=1。實際應用中，取N=3，代入式（1）得到式（2）。

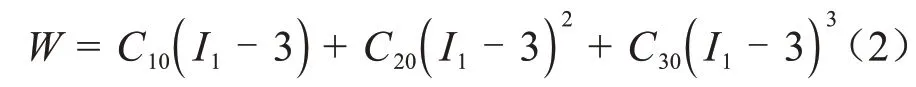
式（2）中：W為應變能密度；I1為第一格林應變不變量；C10、C20、C30為Revlin 系數，其中C10為小應變時的初始剪切模量，在小應變時，橡膠填料網格沒有被破壞，只有C10初始剪切模量起作用；負值的C20體現中等變形時材料的軟化過程；正值的C30體現大變形時材料的硬化。

Yeoh 本構模型擬合精度高，擬合曲線與硅橡膠單軸拉伸力學行為符合。本文利用試驗得到的應力應變數據，將數據導入COMSOL 軟件中，然后擬合出材料本構模型常數，得到常溫25℃，高溫50、75、100℃溫度下絕緣硅橡膠和半導電硅橡膠的本構模型參數分別如表1、表2 所示，可以看出絕緣硅橡膠和半導電硅橡膠在75℃時的初始剪切模量最大。在130℃下老化48、96、144、192、360、528、720 h 的絕緣硅橡膠和半導電硅橡膠擬合本構模型參數分別如表3、表4 所示，可以看出，隨老化時間增加，初始剪切模量C10不斷減小。

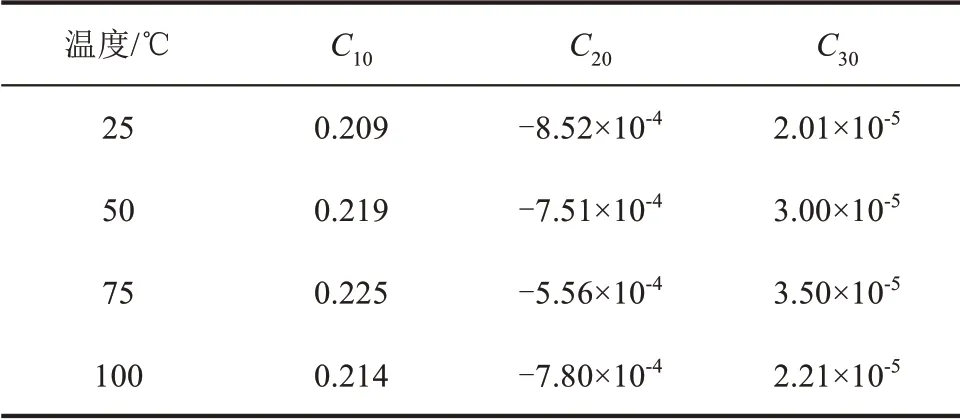
表1 不同溫度下絕緣硅橡膠Yeoh模型參數Tab.1 Fitting results based on Yeoh model for insulating silicone rubber at different temperatures

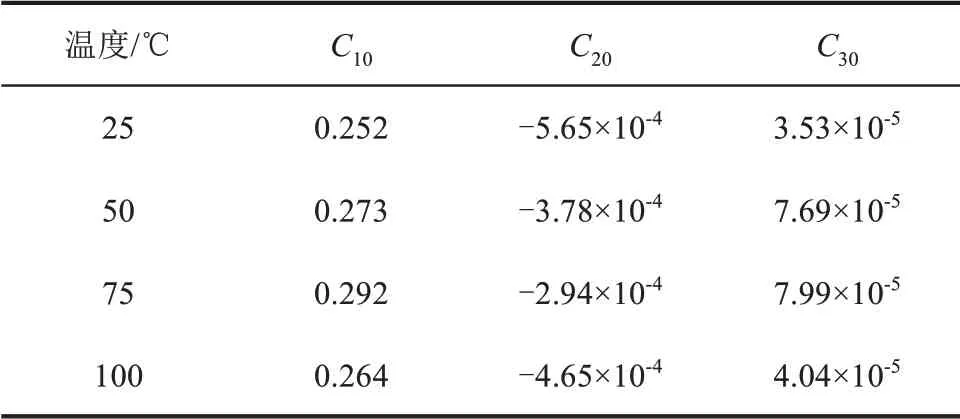
表2 不同溫度下半導電硅橡膠Yeoh模型參數Tab.2 Fitting results based on Yeoh model for semi-conductive silicone rubber at different temperatures

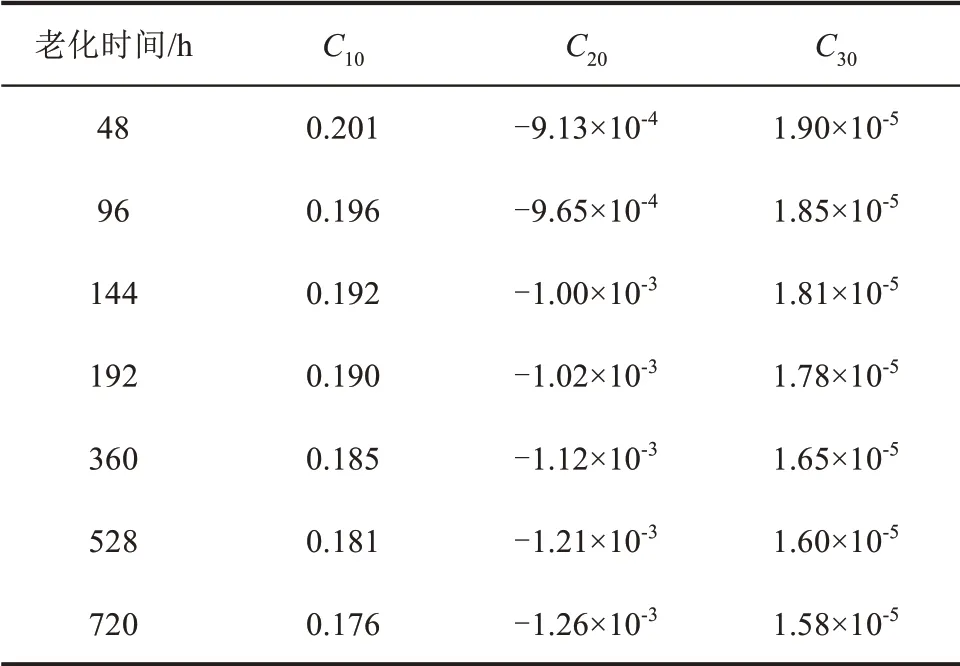
表3 130℃老化下絕緣硅橡膠Yeoh模型參數Tab.3 Fitting results based on Yeoh model for insulating silicone rubber after ageing at 130℃

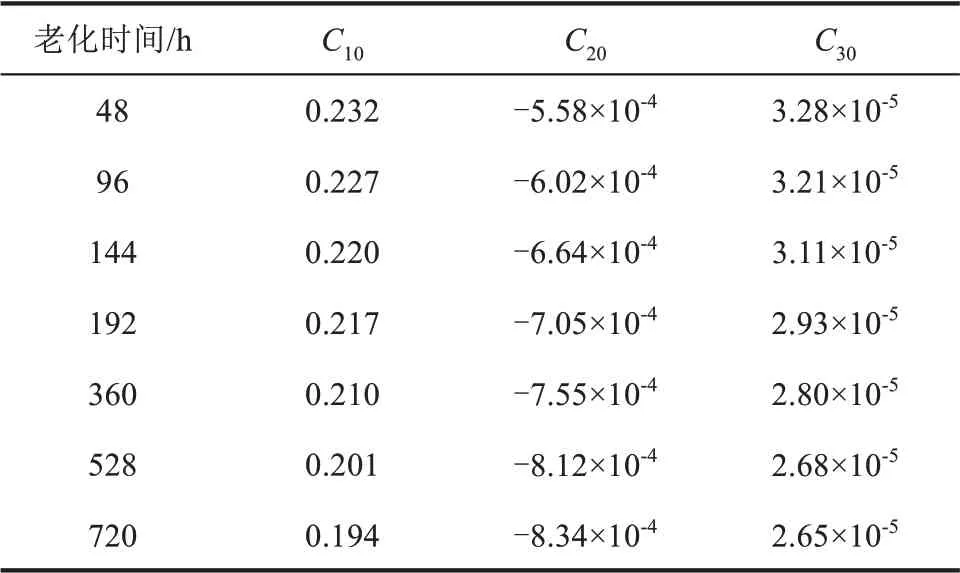
表4 130℃老化下半導電硅橡膠Yeoh模型參數Tab.4 Fitting results based on Yeoh model for semi-conductive silicone rubber after ageing at 130℃

2.3 界面壓力理論計算

橡膠本構關系由應變能密度函數定義，如式（3）所示[13-14]。

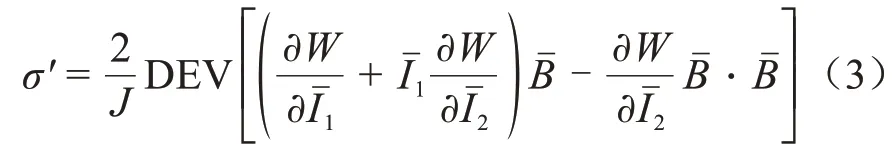
式（3）中：σ′為Cauchy 應力偏量；DEV[?]表示張量[?]的偏量；W為變壓縮前單位體積的應變能密度函數；1與2為應變第一與第二不變量；J是硅橡膠變形前、后的體積比；左Canchy-Green 張量B=F?FT，F為硅橡膠的變形梯度張量。

軸對稱平面應變的3個主伸長量λi(i=r, θ, z)如

式（4）所示。

式（4）中：R為硅橡膠變形前的半徑；r為硅橡膠變形后的半徑。結合式（3），計算可得式（5）。

式（5）中：σr為徑向應力；σθ為環向應力。

半導電材料受壓平衡方程為式（6）。

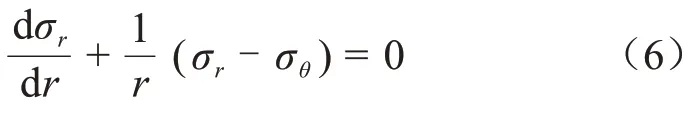
聯立式（2）、式（5）和式（6），可得式（7）。

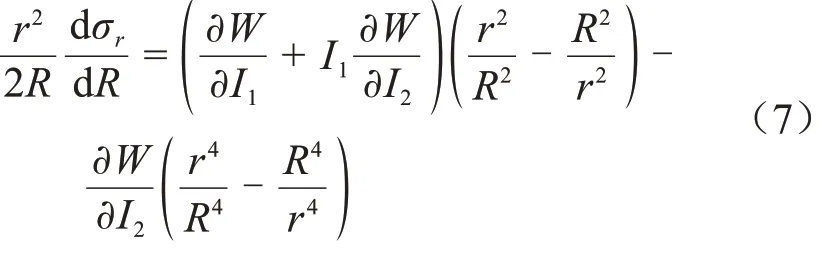
考慮橡膠近似不可壓縮，可得式（8）。

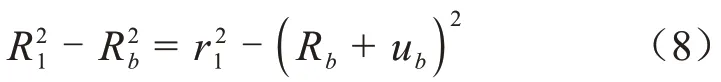
式（8）中：ub表示半導電層在Rb處受到的徑向變形；R1、r1表示絕緣硅橡膠變形前、后的半徑。

對于絕緣層，絕緣硅橡膠外表面徑向應力為0，聯立式（7）和式（8）可以計算得到絕緣層內徑為Rb處的徑向應力（Pb）表達式，如式（9）所示，其中Ra為接頭外徑。

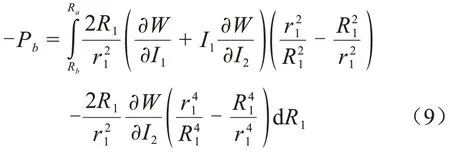
對于半導電層，以Pc和uc分別表示半導電硅橡膠在Rc處的徑向應力和發生的徑向變形，R2、r2表示半導電硅橡膠變形前、后的半徑，則有式（10）。

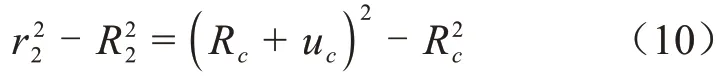
根據式（7）和式（10）可以計算得到電纜接頭內徑處的徑向應力表達式，如式（11）所示。

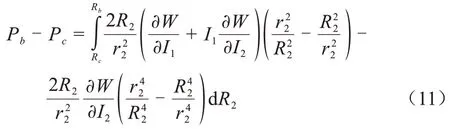
以uc′表示電纜層在Rc處發生的變形，則由縱向應力和接觸界面變形連續性，可得式（12）；電纜層在Rc處徑向應力為Pc，Ec為XLPE 的彈性模量，vc為XLPE的泊松比。過盈配合界面變形關系為式（13）。

由半導電層橡膠的近似不可壓縮性可得式（14）。

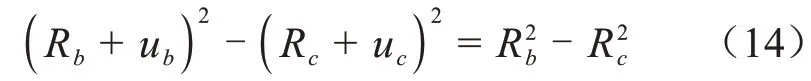
聯立式（9）～（14）可解出電纜接頭與電纜絕緣XLPE 間的界面壓力以及電纜絕緣XLPE 的徑向應力及變形。

2.4 界面壓力分布規律

為了研究電纜中間接頭界面壓力分布規律，將25、50、75、100℃溫度下的附件硅橡膠本構模型參數代入仿真模型，取過盈量為1.5 mm，得到電纜接頭應力云圖如圖7所示，應力錐截面、絕緣硅橡膠截面徑向應力分布和位移形變圖如圖8所示。

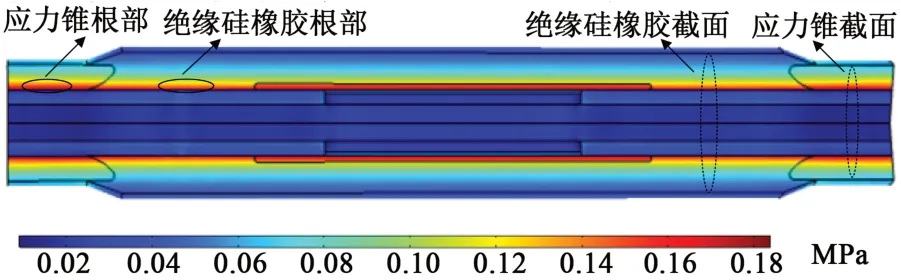
圖7 電纜接頭應力分布云圖Fig.7 Stress distribution map of cable joints

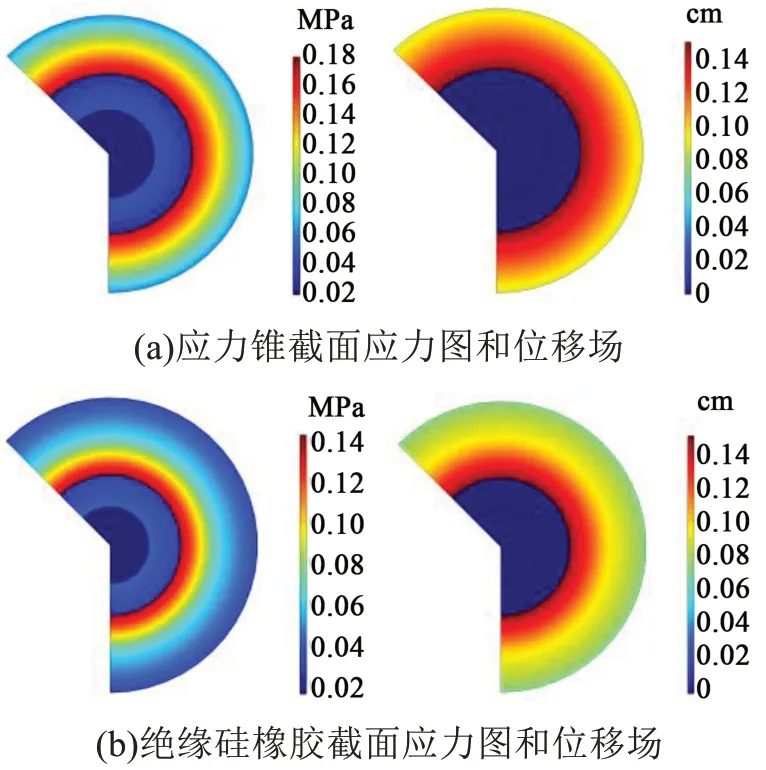
圖8 應力分布和位移場Fig.8 Stress distribution and displacement field

分析圖7～8 得到：電纜接頭為軸對稱結構，中間接頭界面壓力對稱分布，相同半徑圓周上的應力大小相等。附件最大形變出現在附件與交聯聚乙烯XLPE 過盈配合處，其特點是位移形變從接頭內側到外側逐漸減小；附件最大應力出現在附件與交聯聚乙烯XLPE 接觸面，其特點是應力從接頭內側到外側逐漸減小。

圖9為絕緣硅橡膠和半導電硅橡膠根部界面壓力與過盈量的關系圖。從圖9 可以看出，界面壓力隨過盈量線性增加，過盈量每增加0.5 mm，絕緣硅橡膠根部界面壓力增加0.045 5 MPa，半導電絕緣硅橡膠根部界面壓力增加0.057 7 MPa。

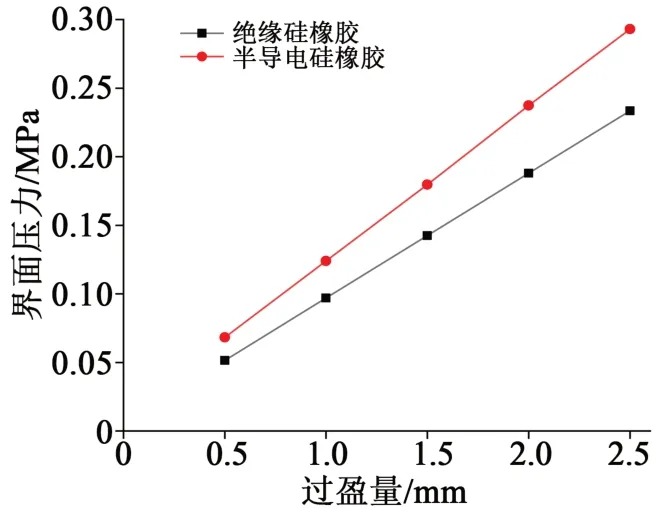
圖9 界面壓力與過盈量Fig.9 Interfacial pressure and interference volume

為了更直觀地研究電纜接頭軸向界面壓力大小，定義接頭應力錐左端為原點，向右為正方向，沿接頭復合界面采集軸向的壓力數據，得到接頭界面壓力分布如圖10所示。

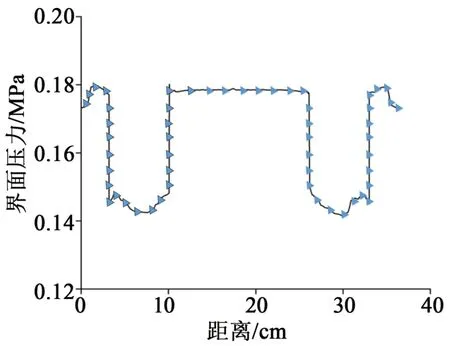
圖10 電纜接頭軸向界面壓力分布Fig.10 Pressure distribution at the axial interface of cable joints

10 kV 電纜冷縮附件兩端為應力錐結構，應力錐界面壓力由半導電硅橡膠壓縮形變產生，由圖10可知，附件外端口壓力為0.173 MPa，在1.1 cm 處上升到0.180 MPa，在3.2 cm 處，界面壓力顯著下降到0.146 MPa。這是因為應力錐厚度減小，絕緣硅橡膠厚度增加，絕緣硅橡膠彈性模量小于應力錐硅橡膠模量，彈性模量對力學性能的計算影響較大。絕緣硅橡膠根部最小界面壓力為0.143 MPa，在10.1 cm處，附件內側材料為高壓屏蔽管，壓力顯著上升到0.179 MPa。由于電纜中間接頭為軸對稱結構，故兩端壓力變化趨勢一樣。

針對電纜接頭的薄弱點，對接頭絕緣與XLPE接觸面、應力錐根部與XLPE 接觸面及高壓屏蔽管與XLPE 接觸面的界面壓力展開理論求解和有限元數值仿真計算，對比理論求解和有限元數值仿真計算結果，結果如表5 所示。從表5 可以看出，理論計算與仿真結果差異較小，偏差在2%以內，二者的吻合度高。

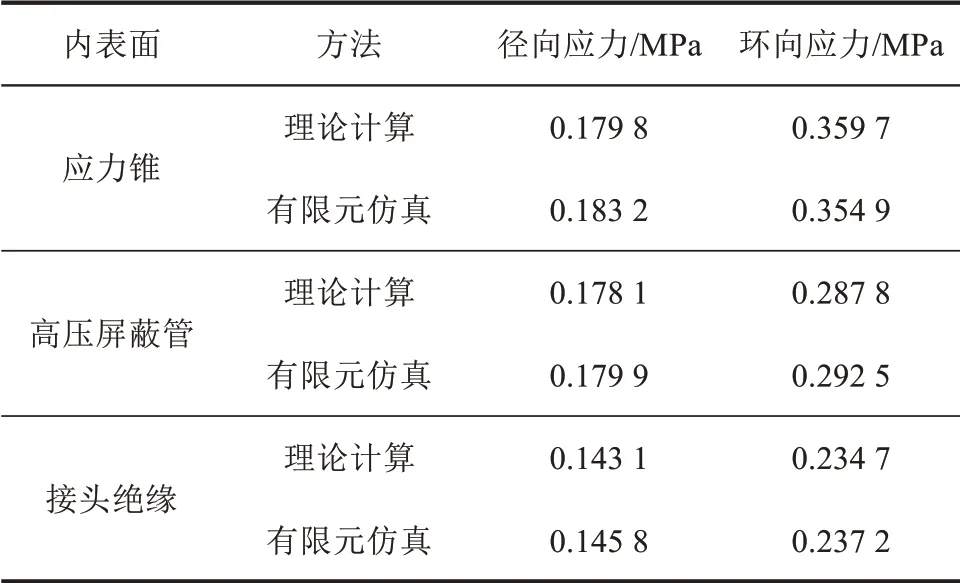
表5 電纜接頭復合界面壓力的計算結果Tab.5 Calculation results of composite interface pressure for cable joints

3 附件高溫對界面壓力的影響

為研究不同溫度下界面壓力對電纜XLPE 形變的影響，設10 kV 電纜銅芯為剛體，電纜銅芯直徑為15 mm，絕緣厚度為6 mm。根據文獻[7]測量的交聯聚乙烯彈性模量隨溫度變化的數值，計算得到XLPE徑向位移量隨壓力的變化關系，如圖11所示。

從圖11可以看出，在界面壓力作用下，XLPE發生一定的徑向位移，當溫度升高時，XLPE 的彈性模量降低，徑向位移量增大。當界面壓力為0.2 MPa時，XLPE在20℃的形變量為2.3 μm，在80℃的形變量為12 μm，形變率分別約為0.15%和0.80%。溫度升高，電纜XLPE的壓縮形變可忽略。

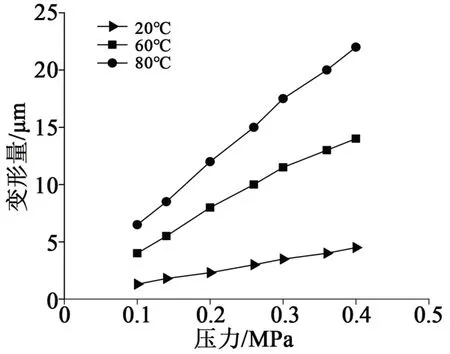
圖11 不同界面壓力下的XLPE徑向位移Fig.11 Radial displacement of XLPE at different interface pressures

為了研究溫度對電纜中間接頭界面壓力的影響，將50、75、100℃溫度下的附件硅橡膠本構模型參數代入仿真模型，計算得到過盈量為1.5 mm時不同溫度下電纜接頭的應力分布云如圖12所示，可以看出在75℃時，界面壓力最大。

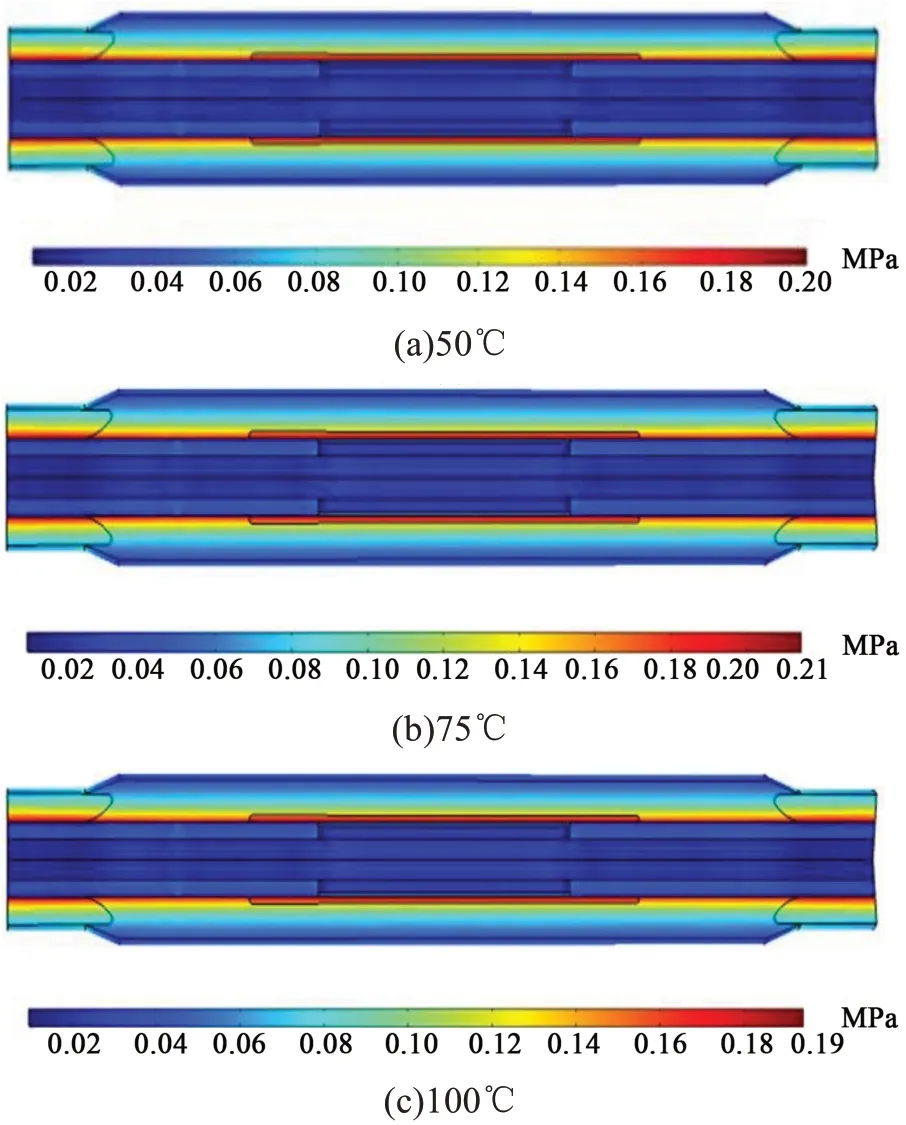
圖12 不同溫度下接頭應力分布云圖Fig.12 Stress distribution maps of cable joints at different temperatures

過盈量為1.5 mm 和2.0 mm 時，應力錐和絕緣硅橡膠根部界面壓力隨溫度的變化關系如圖13 所示。從圖13 可見，溫度為50、75、100℃時絕緣硅橡膠根部界面壓力增加了9.1%、12.3%、6.4%，半導電硅橡膠根部界面壓力增加了9.2%、16.3%、5.6%，電纜接頭在75℃時界面壓力最大。電纜附件硅橡膠為柔順大分子鏈段組成的高聚物，大分子鏈在外力拉伸作用下構象發生改變產生高彈性。由于大分子鏈段對溫度有很強的依賴性，根據交聯橡膠彈性體的彈性模量公式可知彈性模量大小與溫度和彈性體有效交聯密度成比例關系[15-19]。當絕緣硅橡膠和半導電硅橡膠在25～75℃時，隨溫度升高，彈性模量增加，此時構象熵增加占主導因數。當絕緣硅橡膠和半導電硅橡膠在75～100℃時，隨溫度升高，體積發生膨脹，分子鏈間的自由空間加大，分子鏈的熱運動活性變高，運動加劇，有效交聯密度降低，導致分子間作用和鏈段間作用削弱，宏觀表現為橡膠彈性模量降低，說明當硅橡膠溫度超過75℃時，有效交聯密度對橡膠彈性模量起主要貢獻作用。

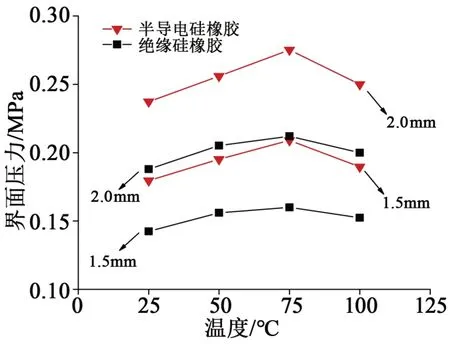
圖13 不同溫度下硅橡膠根部界面壓力Fig.13 Interfacial pressure at the root of silicone rubber at different temperatures

4 附件老化對界面壓力的影響

4.1 界面壓力下降程度

電纜附件在與電纜本體過盈配合時，硅橡膠壓縮產生形變，在硅橡膠單位體積內儲存應變能。為研究熱老化對應力集中單元處應變能密度的影響，選取130℃熱老化的數據計算，結果如圖14所示。

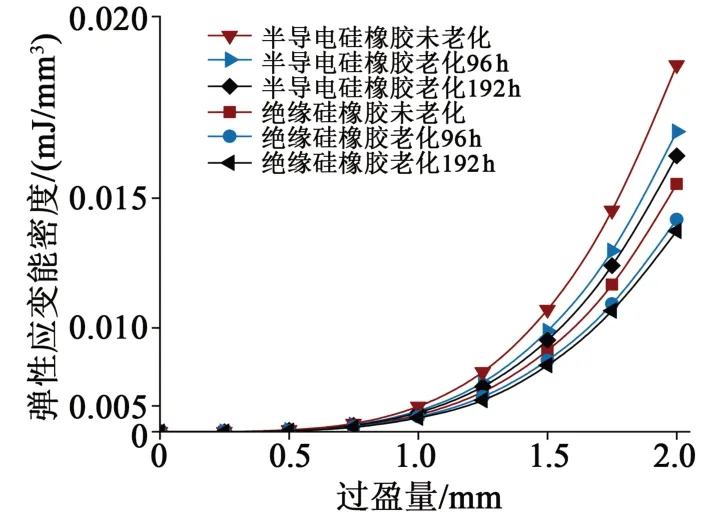
圖14 不同老化時長硅橡膠彈性應變能密度曲線Fig.14 Elastic strain energy density curves of silicone rubber with different ageing time

從圖14可以看出，兩種硅橡膠的彈性應變能密度隨過盈量的增加而增加。在相同過盈量下，半導電硅橡膠的彈性應變能密度大于絕緣硅橡膠的彈性應變能密度。老化后，兩種硅橡膠的應變能密度都減小，在老化192 h，過盈量為2.0 mm 時，半導電硅橡膠的應變能密度減小了13.3%，絕緣硅橡膠的彈性應變能密度減小了10.0%。隨老化時間增加，應變能密度函數斜率變小，反映硅橡膠單位體積積蓄的能量減少，硅橡膠的力學性能降低，從而產生的界面壓力減小。

為研究電纜附件熱老化后的界面壓力變化，通過熱老化實驗獲得在130、150、170℃溫度下老化48、96、192、360、528、720 h 的半導電硅橡膠應力應變曲線，計算在相同過盈量下各老化時間節點的界面壓力下降程度，結果如圖15 所示。從圖15 可以看出，在相同過盈量條件下，隨著老化時間的增加，電纜附件界面壓力減小，且隨著老化的進行呈現出先快后慢的變化規律，在130℃下老化192 h，應力錐根部界面壓力下降了13.6%；而在相同老化時間內，熱老化溫度為150℃時，根部界面壓力下降了24.5%。通過對比不同熱老化溫度下的界面壓力變化率可以看出，溫度對熱老化速率至關重要，熱老化溫度越高，硅橡膠根部界面壓力受到的影響越明顯。

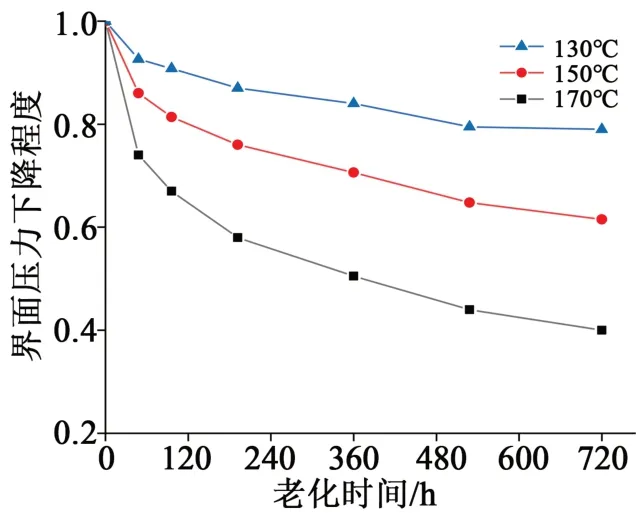
圖15 界面壓力下降程度隨老化時間的變化曲線Fig.15 Curves of the decrease degree in interfacial pressure with ageing time

由于硅橡膠試樣在熱老化初期發生了交聯反應，使得硅橡膠內部形成了更加緊密的網格結構，而交聯度的增加會抑制聚合物鏈間的滑動，降低聚合物的柔順性，破壞硅橡膠原有的高彈性，從而導致絕緣硅橡膠的根部界面壓力降低。當絕緣硅橡膠受到長時間高溫的作用時，分子鏈的運動加劇，當超過化學鍵的離解能時，就會引起高分子鏈的熱降解，且隨著老化時間的增加，熱降解反應逐漸占據主導地位，造成硅橡膠材料大分子鏈斷裂嚴重，導致其力學性能下降，最終使硅橡膠彈性減小，甚至失去彈性[20-22]。

4.2 老化預測模型

硅橡膠的老化性能降低率又被稱為老化程度（P），在本研究中采用老化前后硅橡膠根部界面壓力的下降程度表示。

在一定溫度T下老化，橡膠形變產生的界面壓力隨時間減小，采用文獻[23]提出的修正公式對界面壓力下降程度P和老化時間t進行擬合，如式（15）所示。

式（15）中：P為任意時刻t的界面壓力Pt與初始壓力P0的比值；α為與T無關的常數；k為與T有關的速度常數。在一定溫度下，速率常數k與老化溫度T之間的關系服從Arrhenius公式，如式（16）所示。

式（16）中：A為碰撞因子；E為表觀活化能；R為氣體常數；T為老化溫度。采用逐次逼近的方法求解待定參數，逼近準則為使式（17）中I值最小。

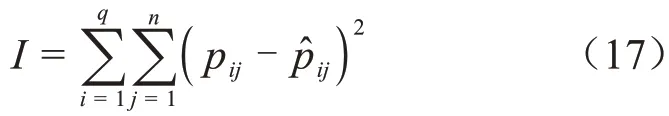
式（17）中：I為逼近準則；pij為第i個溫度下第j個測試點性能的試驗值；?ij為第i個老化溫度下第j個試驗點性能的計算值。通過計算得到在α=0.43 時，I值最小。

根據式（15）擬合lnP和tα的直線關系式，得到各溫度下的速率常數，分別為k130=0.053，k150=0.114，k170=0.219。對式（16）進行對數變換，將速率常數公式變換為式（18）的直線關系式，將k130、k150、k170值取對數，對lgk和T-1進行線性擬合。

式（18）中，Y=lgk，C=lgA，D=E/(2.303R)，Z=T-1。運用最小二乘法計算線性方程的系數C和D，利用r檢驗計算線性相關系數，相關系數r的值都大于0.95，說明相關性顯著，預測值可信。得到速率常數k與老化溫度T的關系式為式（19）。

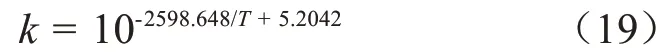
綜上，得到老化預測模型如式（20）所示。

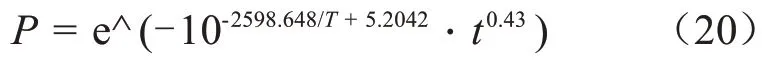
已知冷縮附件的最小初始界面壓力為0.18 MPa，電纜運行的最高溫度為90℃（363 K），滿足電氣要求的最小界面壓力為0.1 MPa，因此界面壓力應保持在P大于0.55 以上，結果如圖16 所示，使用壽命約為28.9年。

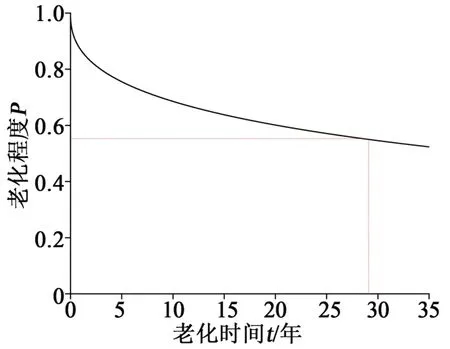
圖16 90℃下老化程度隨老化時間的變化曲線Fig.16 Ageing degree at 90℃changes with ageing time

5 結論

（1）電纜附件最大位移形變出現在附件與交聯聚乙烯過盈配合處，且從附件內側到外側位移形變逐漸減小；附件最大應力出現在與交聯聚乙烯接觸面上，且從附件內側到外側應力逐漸減小。

（2）溫度對附件硅橡膠材料的影響較大，隨溫度升高，兩種材料出現了力學性能改變，通過建立有限元仿真模型分析不同溫度和不同老化時間點的界面壓力變化，在相同過盈量下，與常溫相比，溫度為50、75、100℃時絕緣硅橡膠根部界面壓力增加了9.1%、12.3%、6.4%，半導電硅橡膠根部界面壓力增加了9.2%、16.3%、5.6%，電纜接頭在75℃時界面壓力最大。

（3）附件硅橡膠材料的初始剪切模量隨老化時間的增加而減小，在復合界面水平路徑上，相同節點處，老化前的界面壓力和彈性應變能密度均大于老化后，且界面壓力下降程度隨著老化的進行呈現出先快后慢的變化規律。建立了半導電硅橡膠使用壽命的預測模型，通過預測模型計算，當附件使用溫度為90℃、界面壓力大于初始界面壓力55%時，使用壽命為28.9年。