不同對流層模型對機載精密單點定位的影響分析

董建權，郭將，栗廣才，羅鋒

(1.武漢大學 測繪學院,武漢 430079；2.自然資源部航空地球物理與遙感地質重點實驗室,北京 100083；3.武漢大學衛星導航定位技術研究中心,武漢 430079)

0 引 言

精密單點定位(PPP)是指利用載波相位觀測值以及精密衛星星歷和衛星鐘差來進行高精度單點定位的方法[1].與相對定位不同，PPP 采用單臺全球衛星導航系統(GNSS)接收機，使用精密產品，同時采用精細化改正模型、參數估計或通過組合觀測值的方法對誤差進行改正，以達到高精度定位的目的.由于PPP 無需參考站提供差分值，也就擺脫了距離的限制[2].因此，PPP 技術在低軌衛星定軌[3]、變形監測和災害預報[4-6]、航空測量[7]等領域取得了廣泛應用.

對流層延遲是GNSS 定位的主要誤差源之一，其在天頂(U)方向延遲約為2～3 m，在高度角為10° 時的延遲約為20 m[8].其中，對流層延遲對高程方向定位精度影響最大，而高程測量誤差又是航空重力測量誤差的主要影響因素[9].因此，削弱對流層延遲對PPP 在航空重力測量等領域的應用極為重要.目前，國內外學者對不同對流層延遲改正策略進行了諸多研究，閆志闖等[10]利用分布全球的10 個國際GNSS服務(IGS)站數據分析了三種對流層參數估計方法對PPP 定位精度的影響，得出了單參數方法在U 方向的定位精度與分段常數法相比，最大差異超過了1.5 cm，而附加隨機漫步過程約束的分段常數法與分段常數法定位精度相當的結論；翟樹峰等[11]利用分布于不同區域的IGS 站的觀測數據，比較了不同對流層映射函數對PPP 定位精度的影響，發現VMF1模型和GMF 模型的定位精度相似，而NMF 模型定位精度不如前兩者，并且模型差異會隨季節發生毫米級的變化；熊聚中[12]研究了估計對流層折射的隨機過程方法，提出了一種基于GPS 網的隨機過程方法用于對流層延遲改正，同時也給出了基于最小二乘估計的實現方法，并分析了隨機過程中的參數影響和選擇范圍.但是，目前對流層延遲改正方法的研究主要利用IGS 測站的靜態觀測數據，而對流層模型在機載PPP 的性能還沒有被評估過.因此，本文利用機載數據，分析了GMF、NMF、VMF1、VMF3 作為映射函數，以及作為隨機游走噪聲(RWN)參數對PPP 的影響.

1 對流層延遲改正

1.1 基本原理

當衛星信號通過對流層時產生折射，傳播速度變慢，傳播路徑彎曲.若真空中的折射系數n為1，則對流層延遲計算公式為

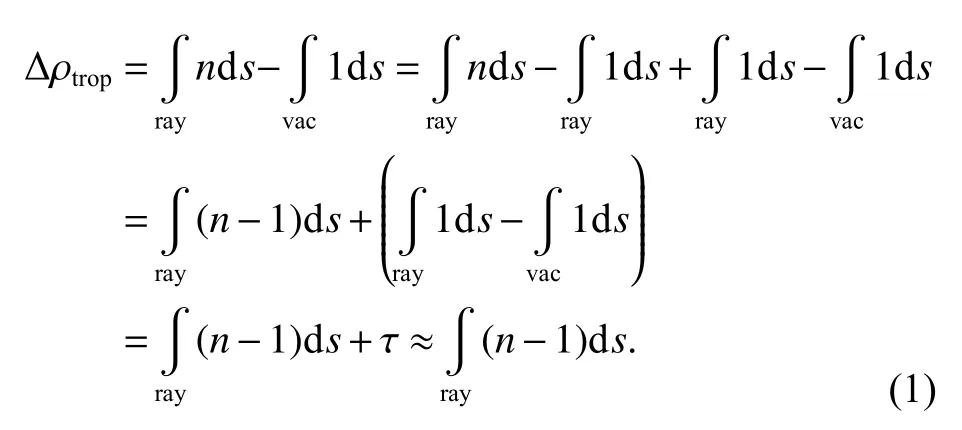
式中：n為對流層中某處的大氣折射系數；ray 和 vac 分別為信號的實際和理論(沿直線)傳播路徑；τ 為路徑彎曲，通常可忽略[13].

由于 (n-1) 的數值很小，為方便計算，常令N=(n-1)×106，并將N稱為大氣折射指數.大氣折射指數N可分為流體靜力學部分(干氣部分)Nd和非流體靜力學部分(濕氣部分)Nw.相應地，對流層延遲可表示為

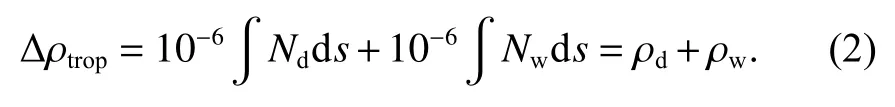
式中：ρd為對流層延遲干分量，主要由干燥氣體折射產生，占整個延遲量的80%～90%；ρw為對流層延遲濕分量，主要由水蒸氣折射產生，占整個延遲量的10%～20%.干分量部分通常采用對流層模型進行改正.而濕分量部分極不穩定，在U 方向上的變化可能達到6～8 cm/h，是干分量的3～4 倍[14]，難以完全用數學模型去描述，因此在PPP 中常將其作為待估參數求解.

此外，信號傳播路徑上的對流層延遲可以表示為天頂對流層延遲(ZTD)與投影函數(MF)的乘積，其中，ZTD 是天頂干延遲(ZHD)和天頂濕延遲(ZWD)之和.故(2)式可表示為

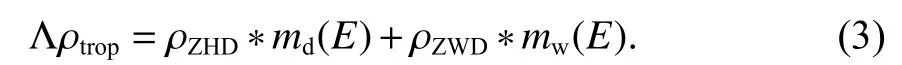
式中：E為衛星高度角；ρZHD和 ρZWD分別為天頂對流層干延遲和天頂對流層濕延遲；md(E) 和mw(E) 分別是相應地干延遲和濕延遲的投影系數.

目前的GNSS 定位一般選取Hopfield[15]、Saastamoinen[16]等模型作為天頂對流層改正模型，再采用合適的映射函數轉換至非U 方向，其常用的投影函數有Marini[17]、NMF[18]、GMF[19]等模型.關于對流層改正模型已有許多文獻研究，本文主要介紹參數估計法和不同映射函數對PPP 的影響.

1.2 參數估計方法

由上述可知，濕延遲在時間和空間上都不穩定，通過模型只能改正約70%的影響，仍存在一部分殘差無法消除.對于高精度定位而言，剩余的殘差仍有較大的影響.這些殘差可以用一個一階高斯-馬爾可夫過程來描述

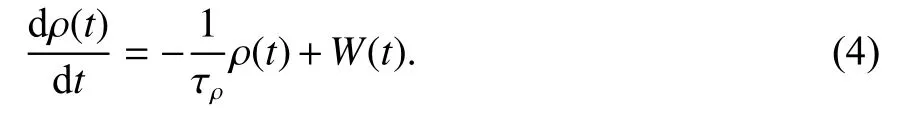
式中：τρ為隨機過程的相關時間；W(t) 是方差為 σ2W的零均值高斯白噪聲

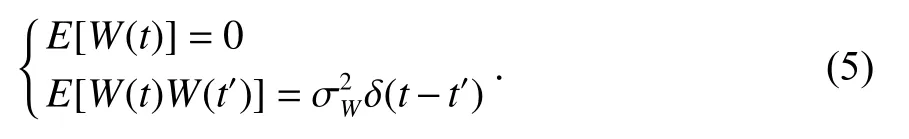
式(1)～(4)的離散解為

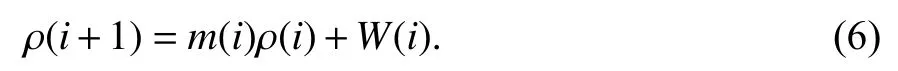
式中，

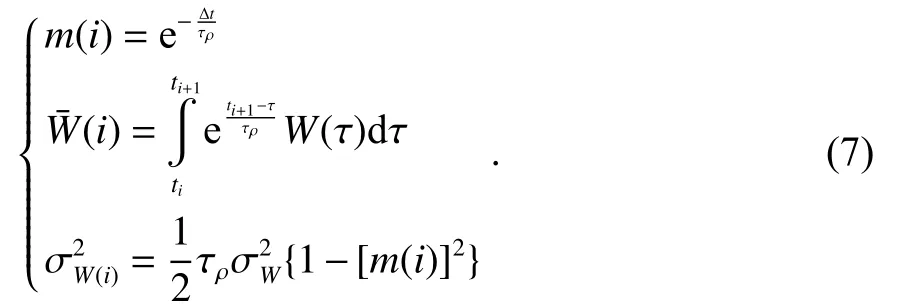
當 τρ→∞ 時，一階高斯-馬爾可夫過程即變為隨機游走過程

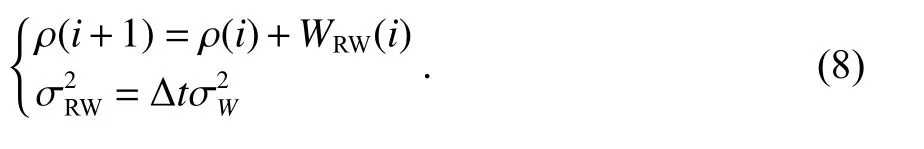
文獻[14]表明：隨機過程估計是目前最理想的對流層折射估計模型，且對于隨機游走過程估計來說，σW的選擇對定位結果有一定的影響.故本文針對不同噪聲參數對PPP 定位結果的影響進行了對比分析.

1.3 映射函數

在PPP 中，映射函數用于將U 方向上的ZTD 投影到傳播方向上，其性能好壞直接影響PPP 的定位精度.隨著國內外學者的研究，目前最常用的映射函數主要有：NMF 模型、VMF 系列模型和GMF 模型，下面分別進行介紹.

1.3.1 NMF 模型

NMF 模型是由Neill 在1996年建立的全球模型[18]，該模型中的映射函數由干分量映射函數md和濕分量映射函數mw兩部分組成.其中，干分量映射函數md的計算公式為

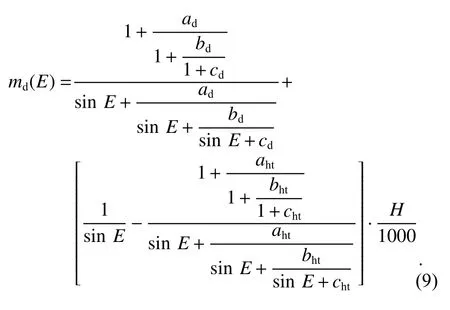
式中：E為高度角；H為正高；通過最小二乘法擬合九個仰角的高度校正得到的高程修改系數：aht=2.53×10-5；bht=5.49×10-3；cht=1.14×10-3.系數ad、bd、cd可由式(10)內插后求得

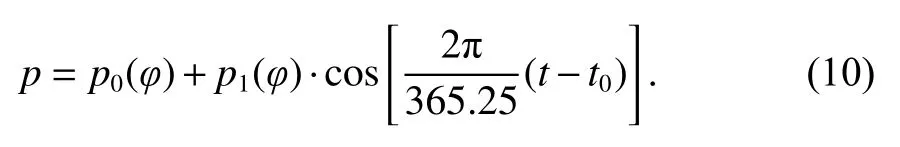
式中：φ為測站緯度；t為年積日；p為系數ad、bd和cd；p0和p1分別為干延遲系數的年平均值和振幅.計算距離測站最近緯度的干延遲系數，如表1所示，最后通過線性插值得到測站處的系數.當測站緯度低于15°或高于75°時取臨界值，不需要進行插值[20].

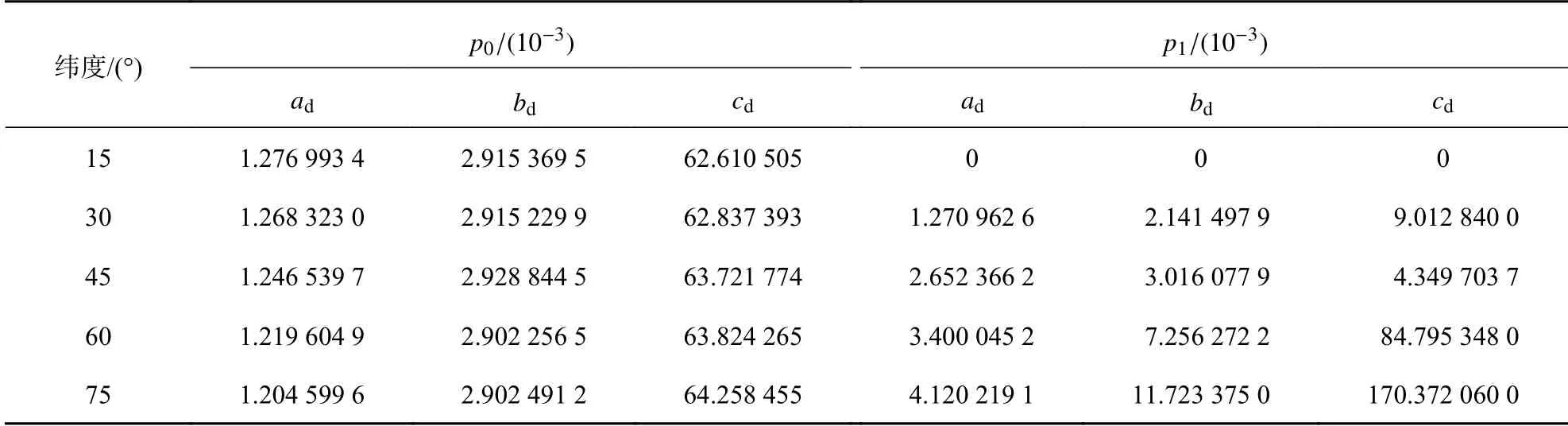
表1 干分量投影函數系數表

濕分量的映射函數mw的計算公式為

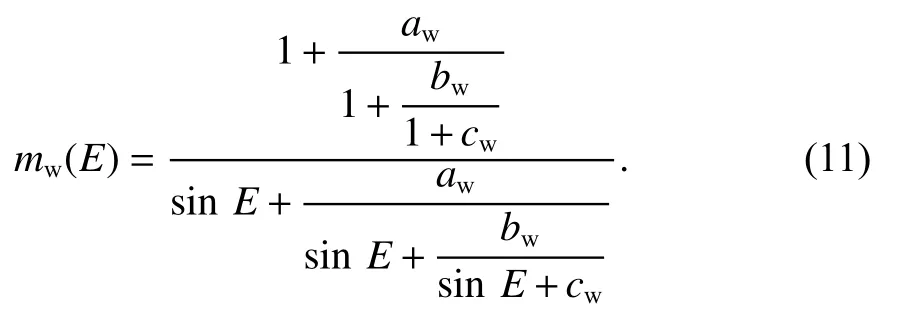
當測站緯度在15°～75°時，對于濕分量的系數aw、bw、cw來說，由于沒有季節變化，因此可直接通過查表2得到分段緯度濕延遲系數，然后對測站進行插值.

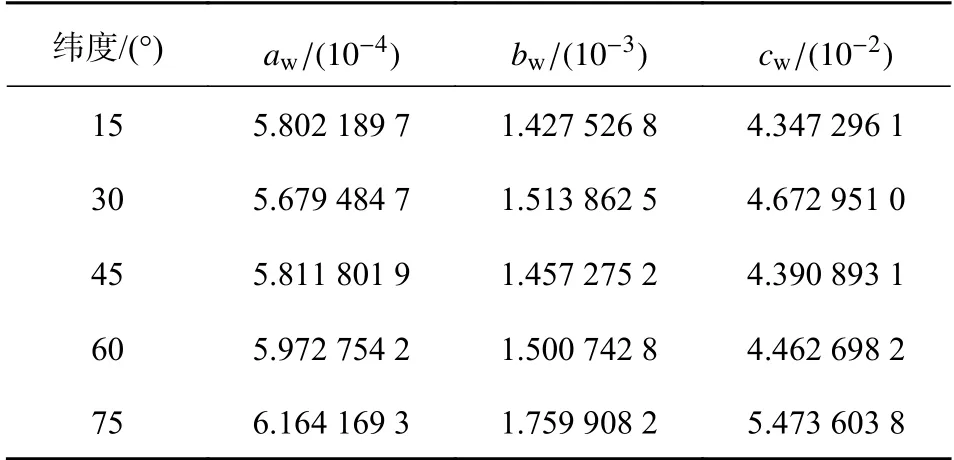
表2 濕分量投影函數系數表

1.3.2 VMF 系列模型

VMF 系列模型是由奧地利維也納理工大學BOEHM 等[19]所建立.從早期的VMF 模型[21]，逐漸發展為VMF1 模型[22]以及VMF3 模型[23]，其形式與NMF 類似，區別就是系數的取值不同.

1) VMF1 模型

VMF1 中的系數ad和aw是該大學依據實測氣象資料而生成的格網圖來提供的，用戶可以從網站上下載，內插后使用，但存在34 h 的延遲.而系數bd、cd則是根據歐洲中尺度天氣預報中心(ECMWF)的氣象資料求得.其中bd為常數，取0.002 9，cd用式(12)計算：

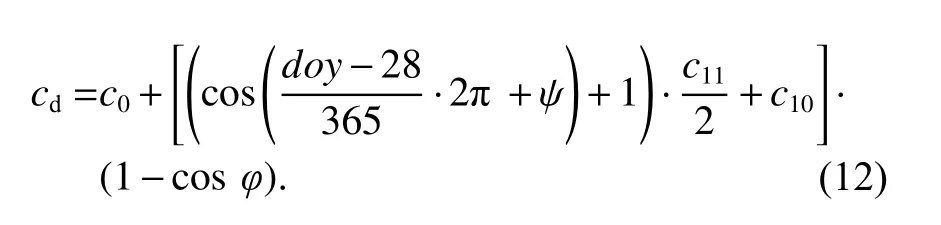
式中：c0=0.062，而c1、c2和φ根據測站位置進行選擇，當測站位于北緯地區時，c10=0.006，c11=0.000，ψ=0；當測站位于南緯地區時，c10=0.006，c11=0.001，ψ=π.bw和cw采用NMF 濕延遲映射函數在緯度為45°處的值，即bw=0.001 46，cw=0.043 91[24].

2) VMF3 模型

Landskron 等在2018年提出了VMF3 模型[23]，VMF3 在低衛星高度角延遲等方面更優于VMF1.其中，干濕系數b、c的計算公式為

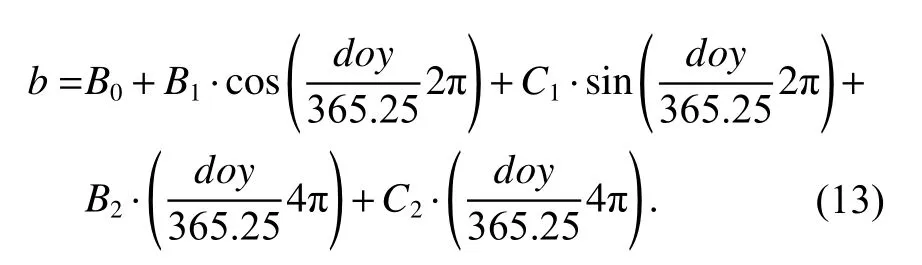
式中：B0為年平均值；B1和C1為年振幅；B2和C2為半周年振幅.VMF3 中的ad和aw可以從網站上下載，也可以直接通過GPT 模型得到，便于進行實時定位.

1.3.3 GMF 模型

為解決VMF1 的時延問題，BOEHM 等[19]又提出了GMF 模型.它借鑒了NMF 模型中的做法而具有較好的精度，又解決了VMF1 的時延問題[25].GMF模型與NMF 模型的區別在于系數不同.在GMF 模型中，ad和aw的計算公式為

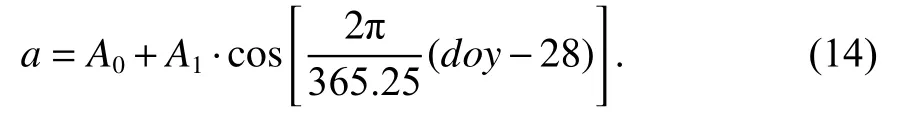
式中：doy是以1980年1月1日為起始歷元計算得到；A0為年平均值；A1為周年振幅，均利用9 階球諧函數展開.bd和cd、bw和cw的計算公式與VMF1 模型相同.

2 實驗分析

2.1 數據獲取及解算軟件

本文采用機載動態數據，數據來源于海南省機載實驗，實驗路徑全長約500 km，具體飛行路徑如圖1所示.飛機搭載NovAtel GPScard 接收機，采集時段從2021-03-27 UTC 06：29：00—11：50：00.

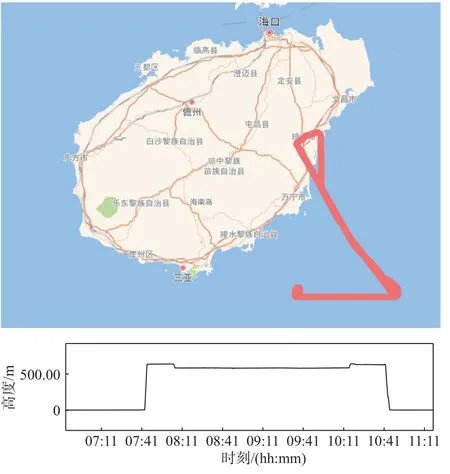
圖1 2021-03-27 機載實驗路徑示意圖

在數據處理時，考慮到雙差解算的定位精度和穩定性整體優于非差解算[26]，使用RTKLIB 軟件雙差解算結果作為坐標的真值參考值.此外，由于飛機和基準站的高差較大，本研究在基線解算時設置了更大的對流層參數過程噪聲來提高雙差模糊度固定成功率，最終基線解模糊度固定成功率達到99.3%，因此可將其作為可靠的參考值使用.然后使用PRIDE PPP-AR 軟件處理動態數據.該軟件可應用于動態移動平臺，適用于航空攝影測量、船載重力測量等，可滿足本實驗解算需求.

2.2 數據處理方法

本文旨在研究不同映射函數對PPP 結果的影響，同時也探究了隨機游走噪聲的選擇對定位精度的影響.在數據處理時，以相對定位結果作為參考真值，基線解模糊度固定成功率達到99.3%.然后使用PRIDE PPP-AR 軟件處理數據，為研究不同映射函數對定位結果的影響，分別選取GMF、NMF、VMF1 和VMF3 作為映射函數進行解算.而實際應用表明，隨機游走參數一般取1 0 ～30 mm/比較合適[14].考慮到對流層延遲對高程比較敏感，且載具運動范圍較大，故本文擴大參數的范圍，選取作為隨機游走噪聲參數，以適應對流層大幅度變化的情況.

解算時位置當作白噪聲(WN)參數來估計，每歷元以標準單點定位解作為初值；接收機參數也當作WN 參數估計，噪聲給定為 9 000 m/；電離層延遲通過無電離層組合消除；需要注意的是由于飛行速度很大，其所處對流層環境變化劇烈，因此本研究采用了每歷元單獨估計對流層參數的策略，具體解算策略如表3所示.

表3 PPP 解算策略

2.3 位置精度對比分析

1)不同模型對定位精度的影響

對獲取的數據進行PPP 解算，分別選取GMF、NMF、VMF1 及VMF3 作為映射函數.圖2顯示了不同映射函數下東(E)、N、U 三個方向誤差序列，表4顯示了不同模型在三個方向定位偏差的均方根(RMS)值.可以看出，四種模型的定位結果大致相同，均在零值附近波動，能起到較好地改正效果.但基于經驗模型GMF 與NMF 的PPP 對流層估值由于沒有考慮氣壓、濕度、地形等信息，其估值非常平穩，只在飛機起飛降落時有“突變”，并沒有很好地描述長距離飛行過程中的對流層變化趨勢.相應地，其高程方向定位誤差偏大，僅為14.13 cm.

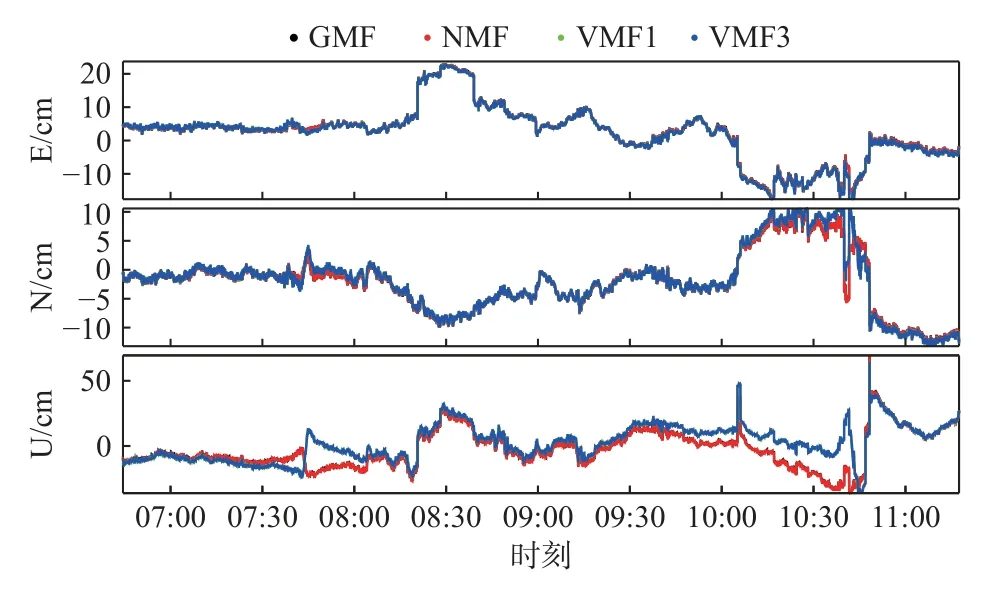
圖2 GMF、NMF、VMF1、VMF3 模型定位結果圖

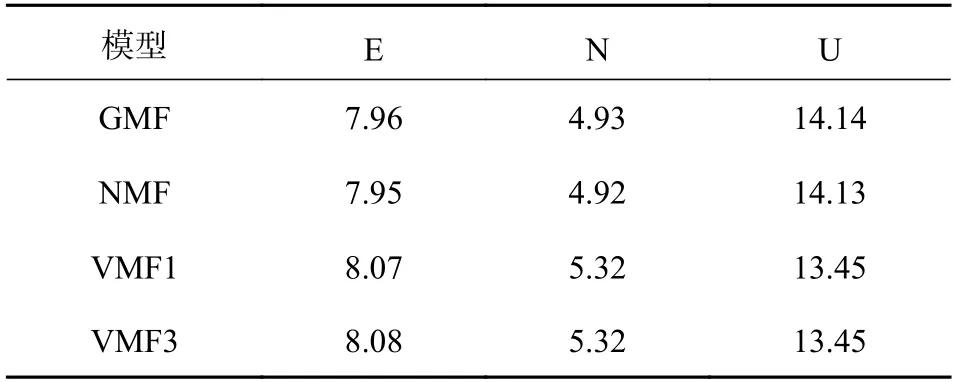
表4 不同模型在E、N、U 方向定位偏差的RMS 值 cm

與經驗模型不同的是，基于精度更高的干分量、濕分量改正的VMF1 和VMF3 在對流層變化劇烈的環境中具有更好的表現，對流層估值相比經驗模型描述了更多“變化細節”.相應地，基于VMF1 模型的PPP 高程方向定位精度達到了13.45 cm，相比GMF模型提高了5%.但在N 方向VMF 模型定位結果較GMF 降低了8%.

2) RWN 對定位精度的影響

為對比RWN 對定位精度的影響，分別設置隨機游走過程的噪聲參數 σ 為映射函數均為VMF3 模型.圖3顯示了不同噪聲參數下E、N、U 三個方向的定位結果與真值偏差的時間序列，表5顯示了不同模型在三個方向定位偏差的RMS.可以看出，隨著 σ 選取的增大，E 和N 方向的定位精度均有所提高并趨于穩定，但 σ 的值過大時，U方向的定位精度則會降低.這說明 σ 的選取對定位精度有一定影響，針對不同需求需選擇合適的 σ 值.

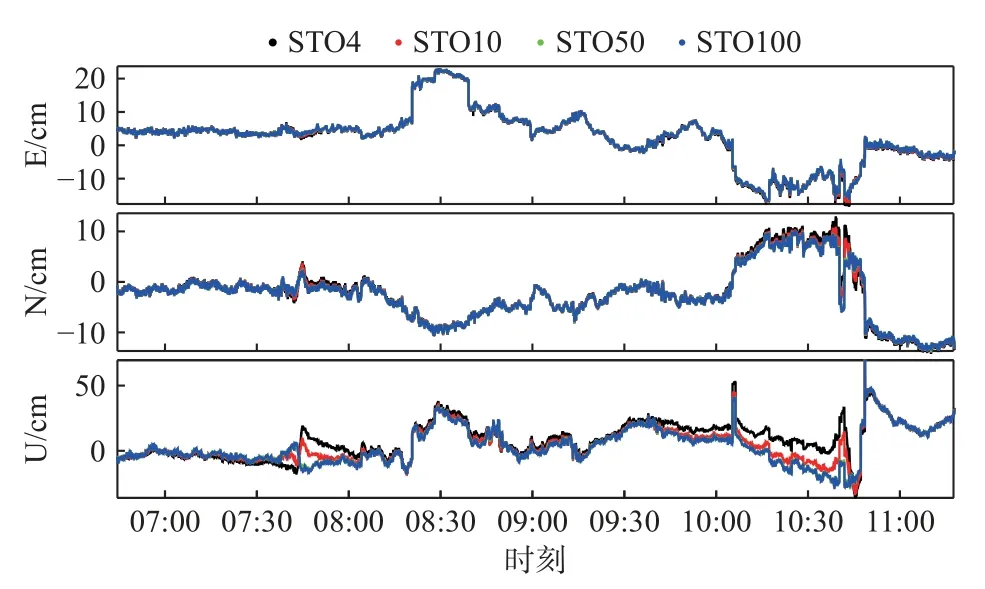
圖3 不同RWN 下PPP 在E、N、U 方向定位結果

表5 不同RWN 下PPP 在E、N、U 方向定位偏差的RMS 值

此外，從上述結果可以看出，不同對流層模型對U 和N 方向定位結果的影響較大，分別達到約3 mm 和4 mm，對E 方向定位結果影響最小，僅有約1 mm.

2.4 ZTD 對比分析

將所得到的數據經PRIDE PPP-AR 軟件處理后，得到了不同模型下的ZTD、ZHD、ZWD 的值，如圖4所示.對比不同模型發現，相比GMF 和NMF 模型，采用VMF1 和VMF3 模型的ZHD 較平穩，未能反映飛機起飛降落時的變化；而對于ZWD 來說，四種模型均能在反映飛機起飛降落時的變化，但VMF1 和VMF3 模型變化較平滑，GMF 和NMF 模型變化較劇烈.

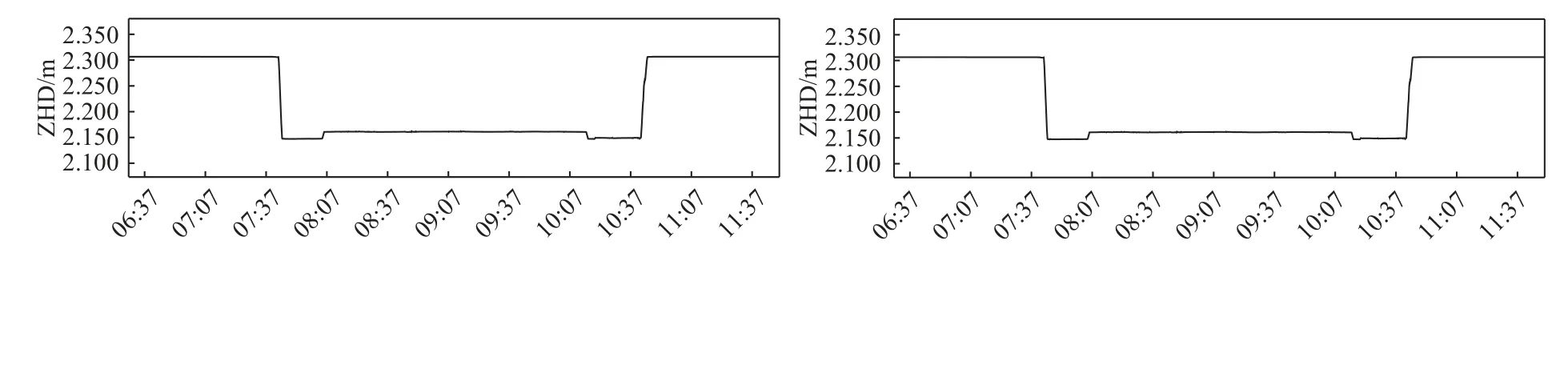
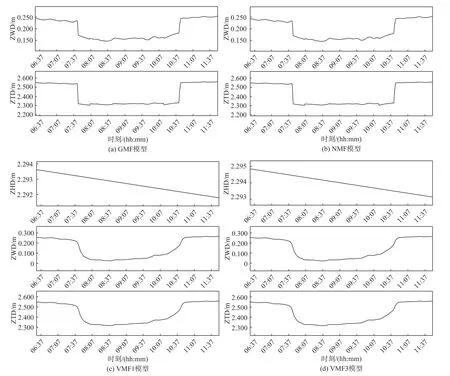
圖4 四種模型的ZHD、ZWD、ZTD 值

而對比不同噪聲發現，噪聲選取對ZTD 估值具有一定影響，噪聲選取越小，ZTD 越平滑，反之則越粗糙，如圖5所示，選擇10 mm/既不會因 σ 太小導致不符合實際，也不會因 σ 太大導致畸變.

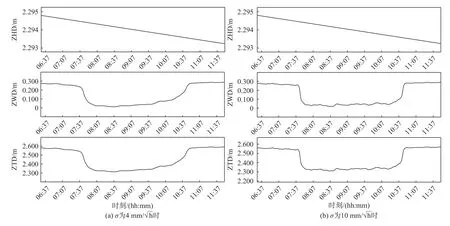
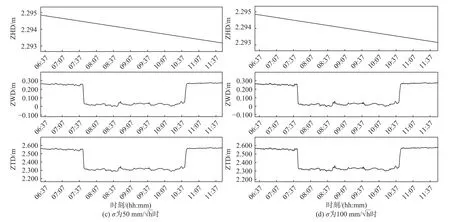
圖5 不同隨機游走噪聲下E、N、U 方向的ZHD、ZWD、ZTD 值

2.5 驗后殘差對比分析

圖6繪制了不同模型定位后相位殘差和偽距殘差.可以看到，對于偽距殘差，幾種模型的結果基本相同.而對于相位殘差，VMF1 和VMF3 模型較GMF和NMF 模型更大，采用1 0 mm/的噪聲后相位殘差有所減小，但還是不如GMF 和NMF 模型.

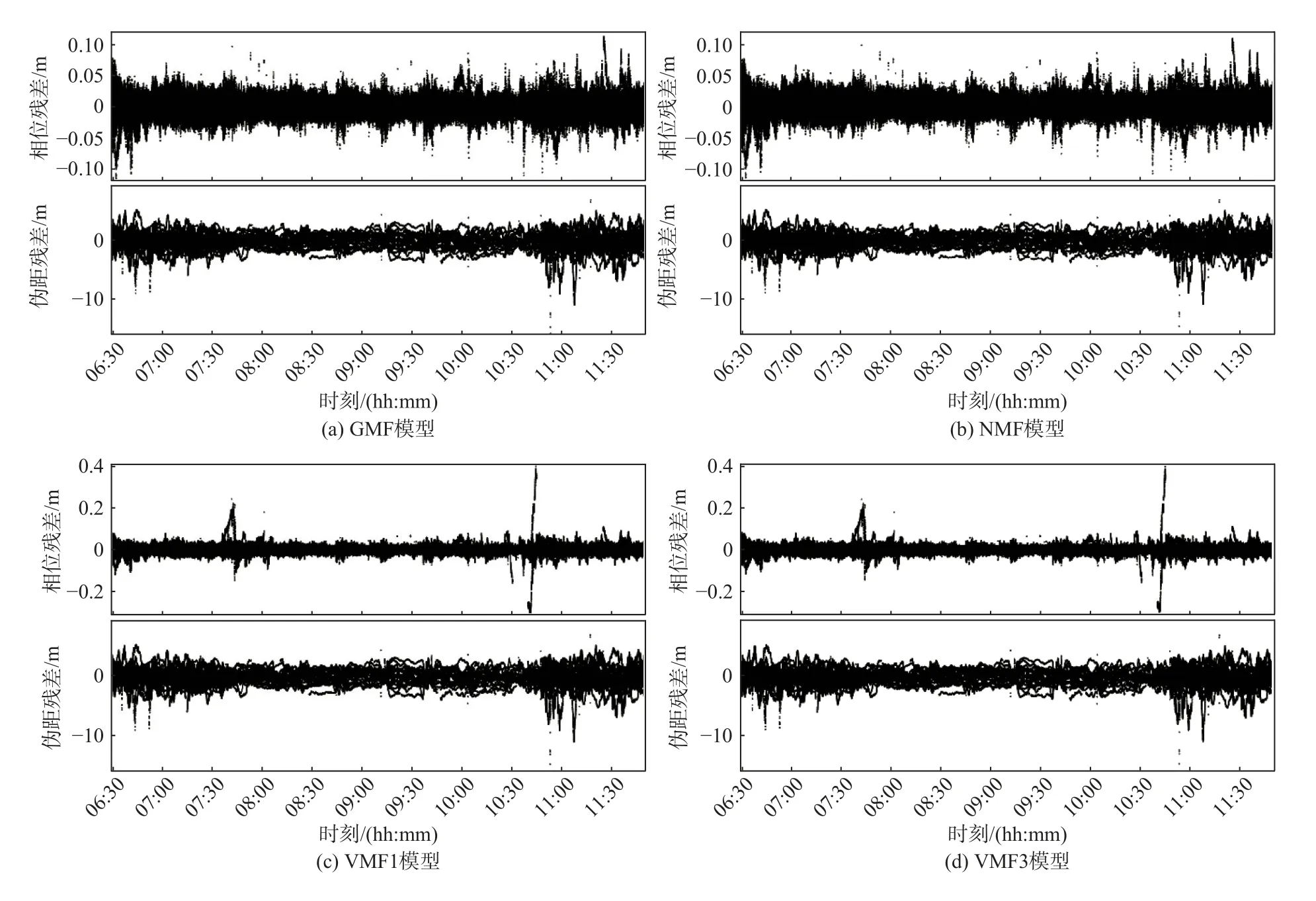
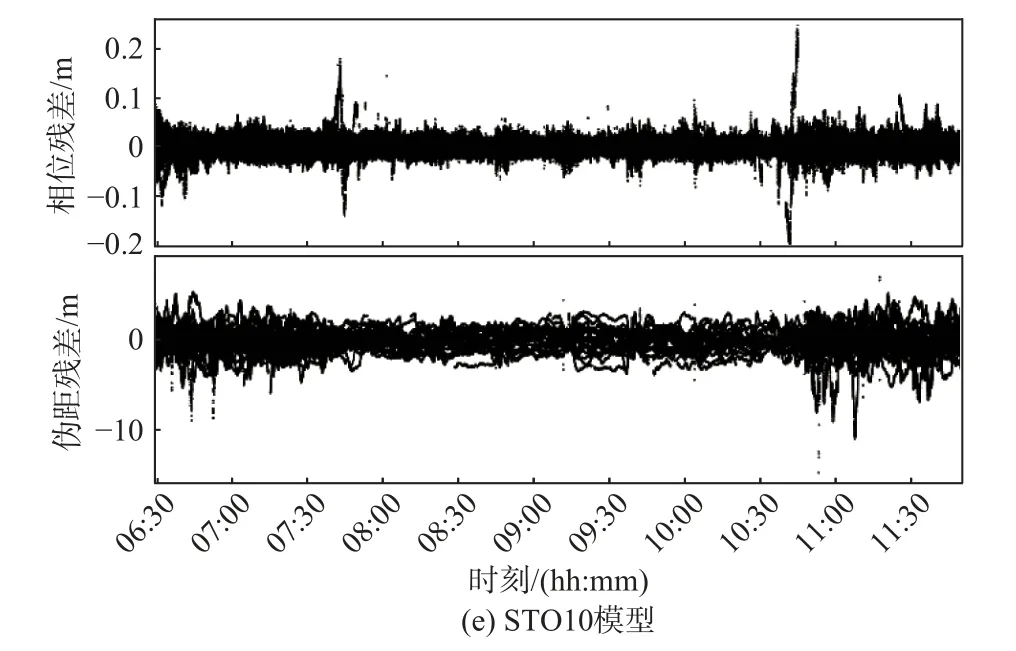
圖6 五種模型的殘差圖

為進一步研究，表6和表7記錄了不同模型下相位殘差和偽距殘差的最大值(Max)、最小值(Min)及GPS、GALONASS、北斗衛星導航系統(BDS)三個衛星系統的RMS 值.對比發現，不同模型偽距殘差僅存在毫米級的差別，而相位殘差存在分米級的差別.其中，VMF1 和VMF3 模型結果較差，RMS 值也略大.

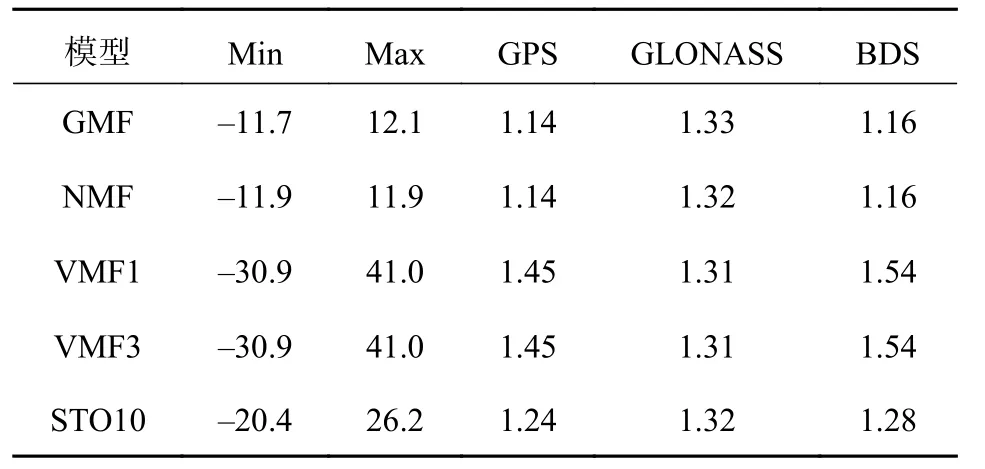
表6 相位殘差的Max、Min 及GPS、GALONASS、BDS 三個衛星系統殘差的RMS 值cm

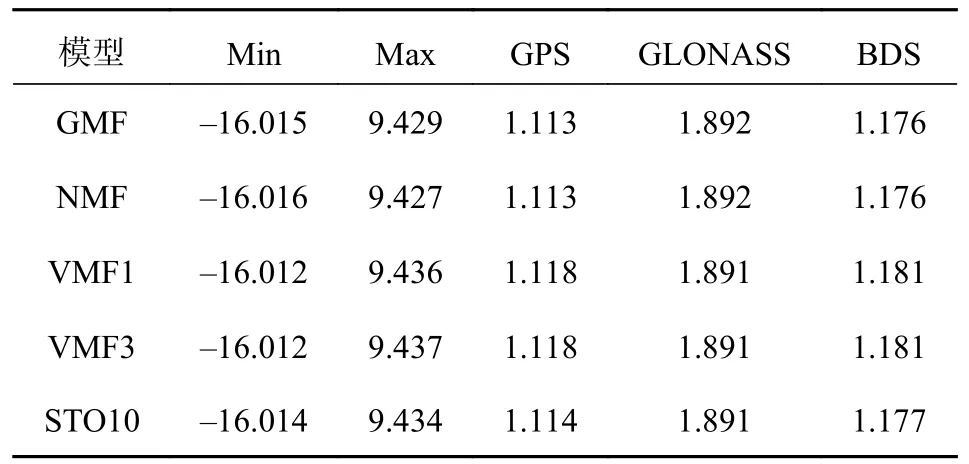
表7 偽距殘差的Max、Min 及GPS、GALONASS、BDS 三個衛星系統的RMS 值m

經檢查后發現，數據中的G09、C09 號衛星殘差結果偏差過大，從圖6中也可以看出VMF 系列相位殘差中有衛星異常突起.這兩顆衛星在觀測弧段平均高度角約30°，推測殘差異常是VMF 系列映射函數與GMF 在低高度角衛星處理上的差異導致.

3 結束語

本文利用開源的PRIDE PPP-AR 軟件對機載實驗獲得的數據進行處理，以相對定位結果作為真值，對比了不同對流層模型、參數估計模型對定位精度的影響.結果表明：

1)不同對流層模型對N、U 方向定位結果影響較大，分別達到約3 mm 和4 mm，對E 方向定位結果影響最小，僅約有1 mm.

2)四種模型均能滿足機載PPP 定位需求，獲得水平厘米級、高程約1～2 dm 的定位精度.其中，VMF1和VMF3 模型定位結果基本相同，GMF 和NMF 模型定位結果基本相同.此外，VMF1 和VMF3 模型在高程方向上定位精度優于GMF 和NMF 模型，提高約5%，但在N 方向VMF 模型定位結果較GMF 降低了8%.因此，針對不同需求應采用合適的對流層模型進行改正，以滿足用戶的定位需求.