基于自適應權重粒子群優化算法的地下水污染溯源辨識

高琬玉，盧文喜，潘紫東，白玉堃

（1.吉林大學地下水與資源環境教育部重點實驗室，吉林長春 130012；2.吉林大學新能源與環境學院，吉林長春 130012）

0 引言

地下水資源具有分布廣泛、不易被污染的特點，是人類生活生產可利用水資源的重要組成部分，其質量好壞是影響環境和生態的重要因素。由于地下水污染［1］具有發生的隱蔽性、發現的滯后性、修復難度大、修復費用高等特點［2］，獲取有效的污染源相關信息是地下水污染修復方案設計的前提條件，因此進行地下水污染溯源辨識具有重要的實際意義。

地下水污染溯源辨識是指利用有限的地下水污染現場實際監測數據（水位和污染物濃度），以及現場調查和專業知識等輔助信息，對地下水污染數值模擬模型進行反演求解，識別確定污染源的個數、位置及釋放歷史（污染質在各時段的釋放強度）等相關信息［3］。在數學上，地下水污染溯源辨識問題屬于數理方程反問題，具有非線性和不適定性的特點，求解難度較大［4］。

有關地下水污染溯源辨識的理論和方法，至目前已有隨機理論與地質統計法、數理方程反演法、同位素法、地球化學指紋法和地球物理探測方法等多種理論方法。總體來講，目前應用的理論和方法中，數理方程反演法中的模擬-優化方法被較為廣泛地應用于辨析確定地下水污染源的分布范圍和釋放歷史等多方面信息、Singh and Datta［5］采用遺傳算法對地下水污染源的位置及污染物質釋放強度進行同步地溯源辨析。Prakash［6］提出了一種基于克里格方法的監測井網優化設計方法，并在此基礎上采用遺傳算法對地下水污染源釋放污染物質的強度進行溯源辨析。Jha and Datta［7］運用模擬-優化方法溯源辨析地下水污染源的釋放歷史，并采用模擬退火算法求解地下水污染溯源辨識的優化模型。Guneshwor et al［8］運用基于粒子群優化算法的無網格流動優化模型溯源辨析地下水污染源的釋放歷史。范小平和李功勝［9］運用一種改進的遺傳算法，溯源辨析山東省某區域地下水中硫酸鹽的年入滲強度。黃林顯等［10］應用模擬-優化方法溯源辨析污染源的位置和污染物質的釋放強度，并利用復合進化算法求解優化模型。隨著智能優化算法的出現，國內外研究學者將其應用于解決地下水污染溯源辨識問題。然而，傳統的智能優化算法存在的早熟收斂問題會導致對反演問題的求解精度不高，針對該問題，國內外研究學者多關注于對算法跳出局部最優能力的提升。Koupaei［11］將混沌映射和黃金分割搜索算法相結合，提高了黃金分割搜索算法的局部搜索能力和快速全局收斂能力。呂石磊［12］提出的基于自適應步長的改進蝙蝠算法有效地避免了過早陷入局部最優和求解精度低的問題。

目前地下水污染溯源識別研究的現狀和發展趨勢具有如下特點：①研究內容多為對單一污染源釋放歷史識別［13］，然而在實際場地中，可能存在需要同時對多個污染源釋放歷史識別的情況。②現階段研究者多運用傳統智能優化算法求解優化模型進行地下水污染源反演識別研究［14］，傳統智能優化算法的求解精度對初始點的依賴較大，易陷入局部最優。

針對上述問題，考慮了多個污染源的情況，對多個污染源的釋放歷史及場地滲透系數聯合識別，應用自適應權重粒子群算法求解優化模型，對算法的迭代終止條件進行改進，對自適應權重優化算法收斂結果影響較大的參數進行修改，大幅度提高了算法的收斂速度和計算精度。

1 研究方法

1.1 模擬-優化方法

在模擬-優化方法中，模擬是指地下水溶質運移模擬模型，用來描述地下水系統輸入（地下水污染源特征、場地水文地質參數等）與輸出（水位及污染物濃度）的激勵-響應關系；優化指的是優化模型，其目的是尋找待識別變量的真實值，即優化模型的最優解［15］。

文章以待識別變量為決策變量、以模擬模型的污染物濃度輸出值與污染物濃度實測差值最小為目標函數建立優化模型，并將地下水溶質運移模擬模型作為待識別變量的等式約束條件嵌入優化模型中，然后運用群智能優化算法求解優化模型［14］。

1.2 拉丁超立方方法

拉丁超立方方法是一種基于分層采樣的方法［16］，能夠反映隨機變量的整體分布。與其它抽樣方法相比［17］，它具有效率高、樣本覆蓋程度好、樣本更具有代表性等優點［18］。對于一維輸入變量，拉丁超立方抽樣原理為：根據需要，確定抽樣數目n，將變量服從的概率密度函數等間隔的分為n個子區間，然后在每個子區間內隨抽取一個值，最后將抽取的n個值進行隨機排列即完成一次抽樣［19］。

根據前人研究，滲透系數對模擬模型的結果影響較大［20］，因此，文章在識別污染源釋放歷史的同時識別滲透系數。采用拉丁超立方方法，在建立模擬模型的替代模型時，對待識別變量進行抽樣，獲得訓練和檢驗替代模型的輸入樣本。

1.3 BP神經網絡

在模擬-優化算法中，優化模型的迭代求解過程需反復多次調用模擬模型，這會帶來龐大的計算負荷，嚴重制約了模擬-優化方法在反演識別實際應用中的可行性［21］，替代模型在功能上逼近模擬模型，能夠以很小的計算負荷逼近模擬模型的輸入-輸出響應關系，因此，研究建立模擬模型的替代模型成為近年來研究進展中的前沿問題之一。采用BP 神經網絡建立替代模型擬合模擬模型的輸出結果。

BP（back propagation）神經網絡是1986 年由Rumelhart 和McClelland 為首的科學家提出的概念，是一種根據誤差逆向傳播使誤差極小化進行訓練的多層前饋神經網絡。它的學習過程由信號的正向傳播與誤差的反向傳播兩個過程組成［22］。它的基本思想為：

（1）先計算每一層的狀態和激活值，直到最后一層（即信號是前向傳播的）；

（2）計算每一層的誤差，誤差的計算過程是從最后一層向前推進的（即信號是反向傳播的）；

（3）更新參數，不斷迭代前兩個步驟，直到滿足停止準則。

其求解過程如下所示：

（1）正向傳播。第l(2 ≤l≤L) 層神經元的狀態及激活值為：

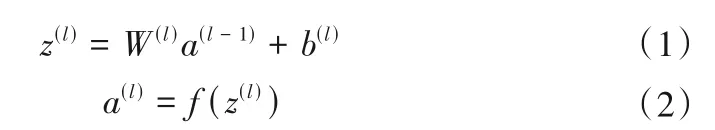
對于L層感知器，網絡的最終輸出為a(l)。前饋神經網絡中信息的前向傳遞過程如下：

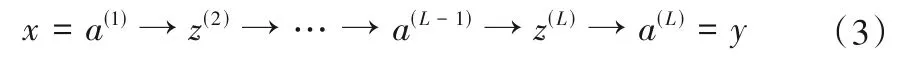
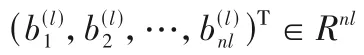
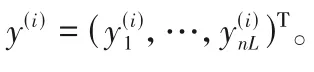
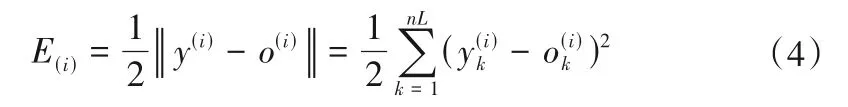
為了調整權重和偏置使總體誤差最小，采用列文伯格-馬夸爾特法求總體誤差最小值，并求此時所對應的各個神經元的參數（即權重和偏置）。

1.4 自適應權重粒子群優化算法

粒子群優化算法（Particle Swarm Optimization，PSO）是模擬鳥類覓食行為的群智能優化算法［23］。鳥類尋找棲息地的過程與尋找特定問題的解的過程類似。設每個優化問題的解是搜索空間中的一只鳥，把鳥視為空間中一個微粒，每個粒子都有一個由被優化函數所決定的適應度值，還有一個速度決定它們的飛行方向和距離。粒子的運動通過追隨當前的最優例子在解空間中搜索最優解。

設n維搜索空間中，粒子i的當前位置為X(i)、當前飛行速度V(i)及所經歷的最好位置P(i)（即具有最好適應度值的位置）分別表示為：

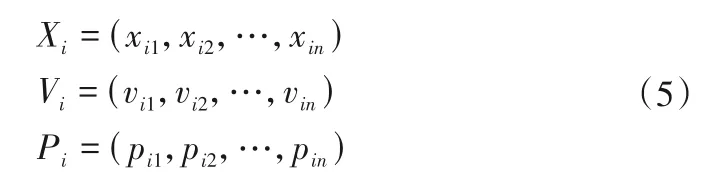
對于最小化問題，若f(X)為最小化的目標函數，則微粒i的當前最好位置由下式確定：

設群體中的粒子數為S，群體中所有粒子所經歷過的最好位置為Pg(t)，稱為全局最好位置，即：

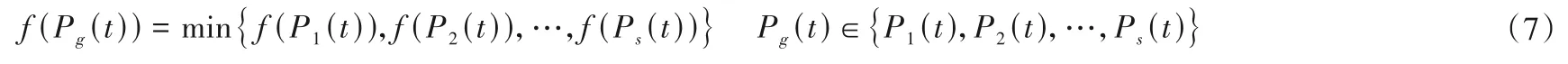
基本粒子群算法粒子i的進化方程可描述為：

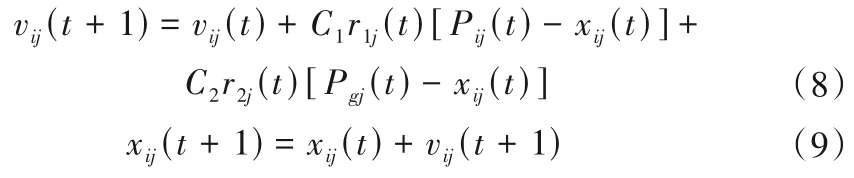
式中：vij(t)為粒子第j維第t代的運動速度；C1、C2為加速度常數（學習因子）；r1j、r2j分別為兩個相互獨立的隨機數；Pg(t)為全局最好粒子的位置。式（8）描述了粒子i在搜索空間中以一定的速度飛行，這個速度要根據自身的飛行經歷［式（8）中右側第2項］和同伴的飛行經歷［式（8）中右側第3項］進行動態調整。

帶有慣性因子的粒子群優化算法是對于式（8）中的vij(t)項加以慣性權重ω，即：

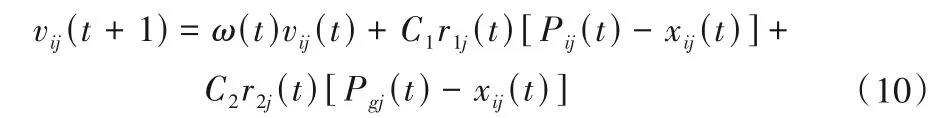
粒子群優化算法有記憶，所以所有粒子都能保留關于當前最優解的信息［24］。粒子之間有建設性的合作，群中的粒子之間共享信息［25］。然而，簡單粒子群優化算法的性能在很大程度上取決于其參數（包括學習因子C1、C2和慣性權重ω），并且經常遇到陷入局部最優從而過早收斂的問題，適當控制全局搜索和局部搜索對于有效地找到最優解至關重要。應用自適應慣性權重因子（AIWF）控制全局搜索求解地下水污染溯源識別問題的優化模型。基本思想如下：如果適應度開始停滯時，粒子群搜索會從鄰域模式向全局模式轉換，一旦適應度開始下降，則又恢復到鄰域模式，以免陷入局部最優。當適應度的停滯次數足夠大時，慣性系數開始逐漸變小，從而利于局部搜索［26］。其中，自適應權重公式如下：

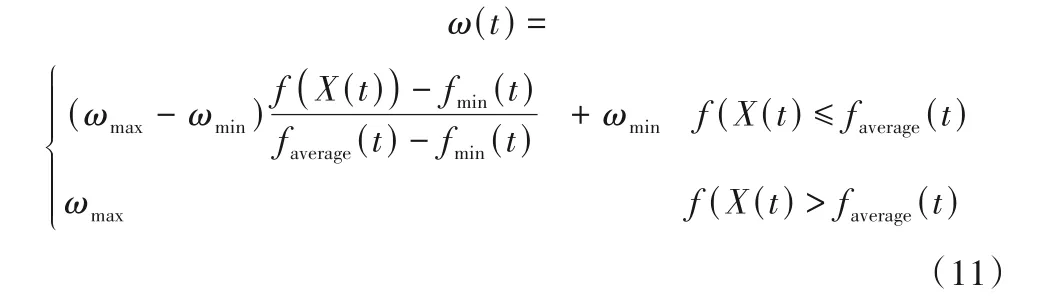
式中：ωmin和ωmax是預先給定的最小慣性系數和最大慣性系數，一般取0.4 和0.9；式（12）為第t次迭代時所有粒子的平均適應度；式（13）為第t次迭代時所有粒子的最小適應度。

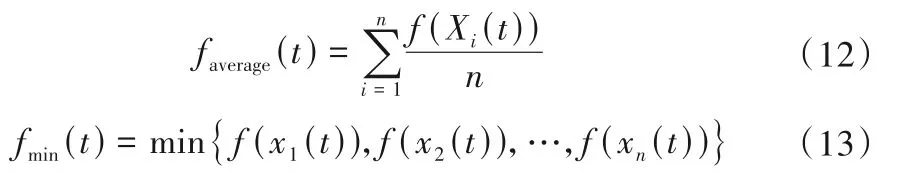
當粒子已經找到最佳位置后，再增加迭代次數會浪費計算時間，因此，采用了自動退出迭代循環的方法。

（1）初始化最大迭代次數、計數器以及最大計數值，分別取1 200，0，20；

（2）定義“函數變化量容忍度”，一般取非常小的正數，取10-6；

（3）在迭代的過程中，每次計算出來最佳適應度后，都計算該適應度和上一次迭代時最佳適應度的變化量（取絕對值）；

（4）判斷這個變化量和“函數變化量容忍度”的相對大小，如果前者小，則計數器加1；否則計數器清0；

（5）不斷重復這個過程，有以下兩種可能：①此時還沒有超過最大迭代次數，計數器的值超過了最大計數值，那么直接跳出迭代循環，搜索結束。②此時已經達到了最大迭代次數，那么直接跳出循環，搜索結束。

2 案例應用

2.1 問題概述

文章參考潘紫東等作者的假想算例，考慮了3 個污染源同時污染的情況，根據9口監測井5次監測數據（45維），同時識別3個污染源五段釋放歷史以及含水層參數（19維）［27］。如圖1所示，研究區概化為二維非均質各向同性的不規則承壓含水層（2 000 m×2 500 m），用邊長為20 m 的正方形將研究區剖分為100×125個有限差分網格。研究區的滲透系數按介質顆粒分為K1、K2、K3、K44 個分區，南北邊界為已知流量邊界，東西邊界為已知水頭邊界，含水層和污染源的相關值和范圍見表1。模擬時間為5 年，每1 年記為1 個應力期。研究區內存在3 個潛在的污染源，在應力期內向含水層排放污染物。建立9 口監測井（Obs1～Obs9），在應力期內每年對含水層中的污染物濃度進行監測。

表1 含水層與污染源相關參數Tab.1 Parameters of pollution sources and aquifer

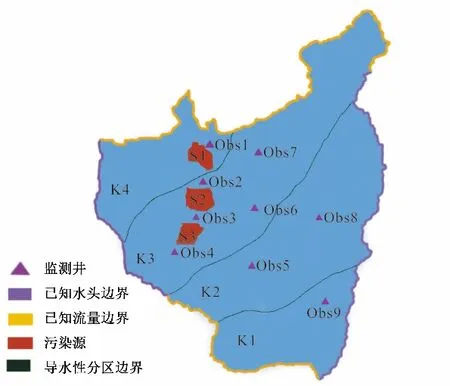
圖1 研究區概況Fig.1 Overview of the study area

2.2 模擬模型建立

根據研究區水文地質概念模型，建立研究區地下水水流的數學模型：

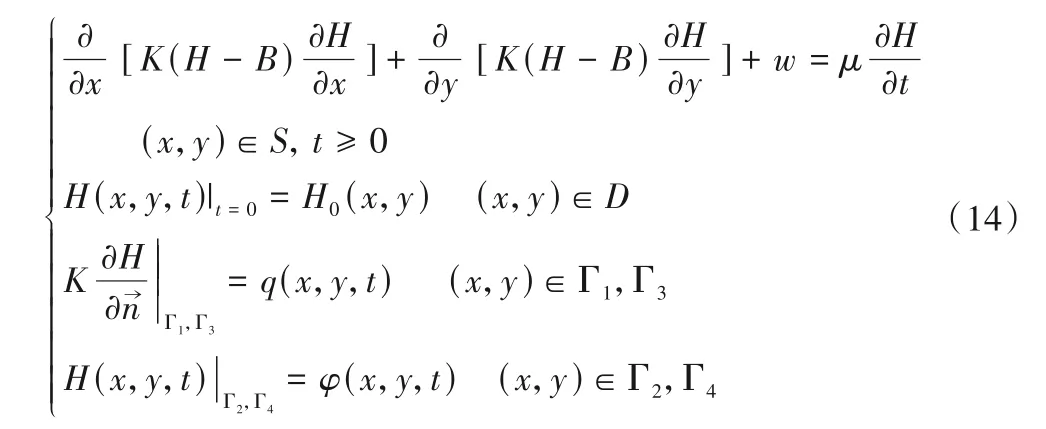
式中：t為時間變量；K為滲透系數；H為水位高程；B為底板高程；w為源匯項；μ為給水度；Γ1，Γ3為已知流量邊界；Γ2，Γ4為已知水頭邊界；q(x，y，t)和φ(x，y，t)為已知函數；n?為邊界上某點(x，y)處外法線方向上的單位向量。

在地下水流數學模擬模型的基礎上，建立地下水溶質運移數學模型：

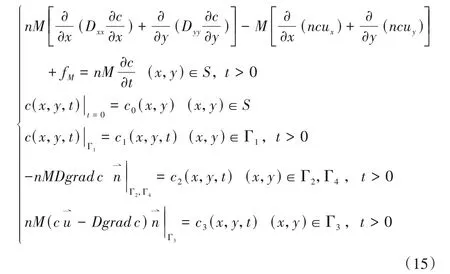
式中：n為孔隙度；M為承壓含水層的厚度；fM為源匯項，表示單位時間含水層單位面積溶質的增減量；c為地下水溶質濃度；Dxx、Dyy是x、y軸方向上的水動力彌散系數；ux、uy分別為實際平均流速向量u?在x、y軸向上的分量；S為研究區；Γ1為已知濃度邊界；Γ2和Γ4為已知水動力彌散通量邊界；Γ3為已知對流-彌散通量邊界；c0(x，y)，c1(x，y，t)，c2(x，y，t)，c3(x，y，t)為已知函數。

利用GMS 軟件中的MODFLOW 和MT3DMS 對地下水流動和污染物運移過程進行了計算，模擬模型的計算結果如圖2所示。

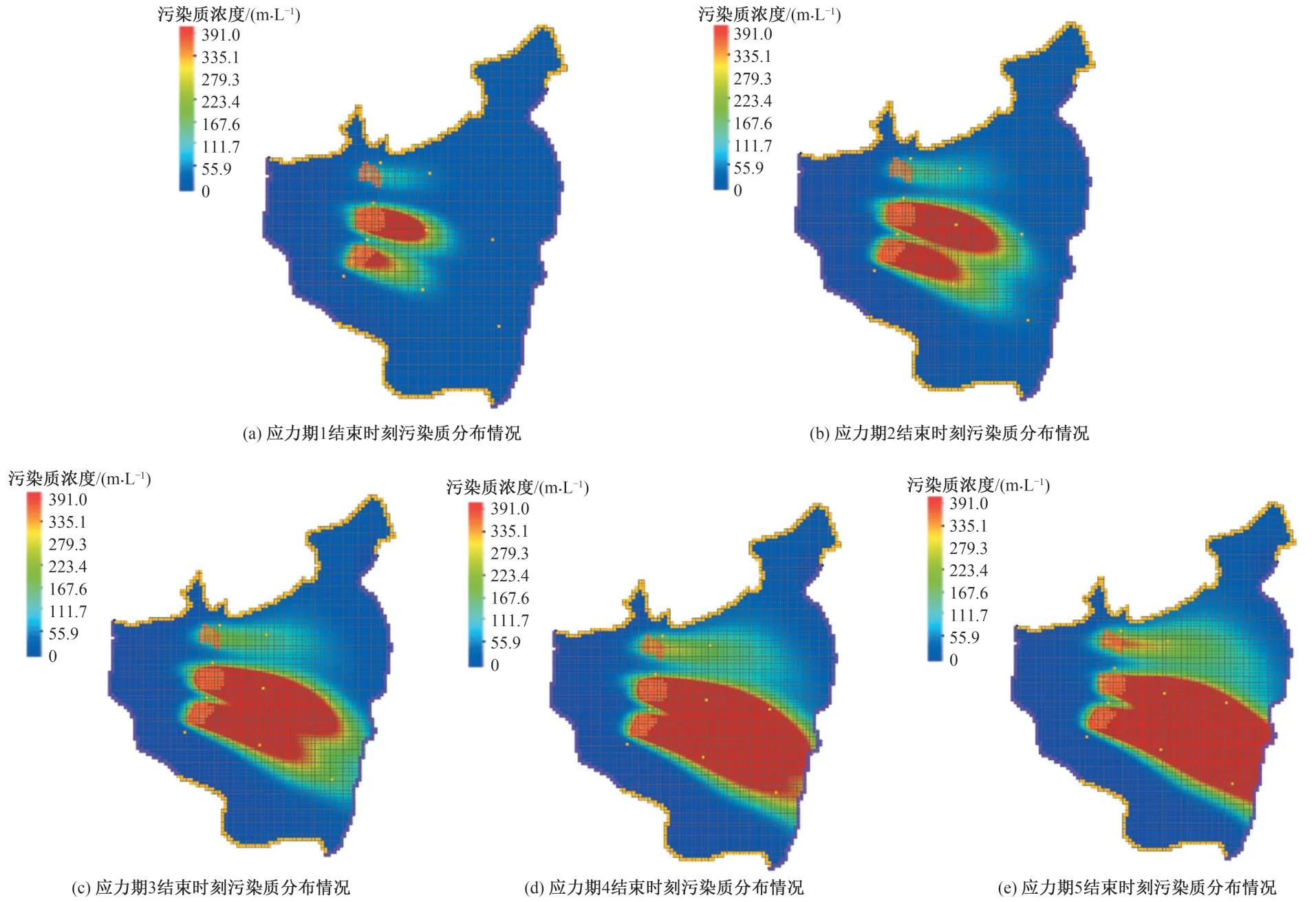
圖2 污染質分布情況示意Fig.2 Distribution of contaminants

由于是一個假想案例，因此，需要人為設定一組待識別變量的值作為真實值，輸入模擬模型，運行獲得每個時期觀測井的污染物濃度，將模擬獲得的觀測井污染物濃度視為實際監測井濃度。待識別的滲透系數真實值見表2；待識別的真實污染源信息見表3。

表2 滲透系數Tab.2 Hydraulic conductivity

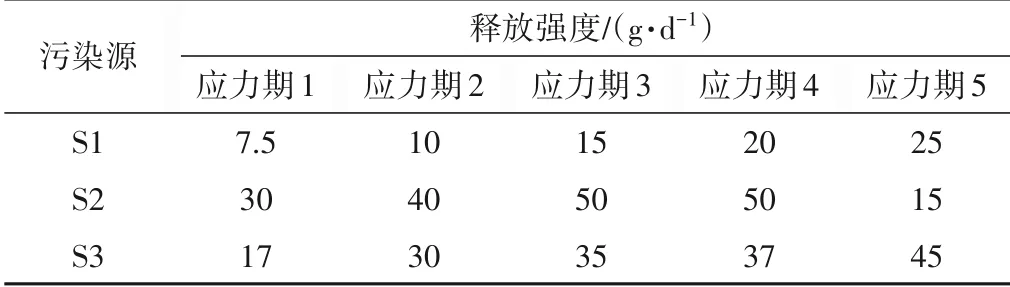
表3 污染源信息Tab.3 Information of pollution sources

2.3 替代模型的建立

利用拉丁超立方方法對19 個輸入變量（4 個滲透系數和3個污染源各5 個時段的釋放強度）進行抽樣，抽取400 組分布較均勻的樣本作為輸入值。將400 組樣本輸入值分別代入GMS軟件進行計算，計算得到400組9個觀測點5年的污染物濃度觀測數據作為樣本輸出值。

將400 組樣本隨機選取280 組作為樣本訓練，60 組作為驗證集，60 組作為測試集。運用列文伯格-馬夸爾特方法訓練BP神經網絡。

訓練集的擬合情況如圖3（a）所示，驗證集擬合情況如圖3（b）所示，測試集的擬合情況如圖3（c）所示，整體的擬合情況如圖3（d）所示。

由圖3的數據可以看出，由BP神經網絡建立的替代模型所求得的輸出與模擬模型計算所求得的輸出，二者之間擬合精度較高，將真實的滲透系數和污染源釋放強度等輸入代入到替代模型中，將求得的輸出與觀測數據進行對比，其擬合程度如圖4所示。

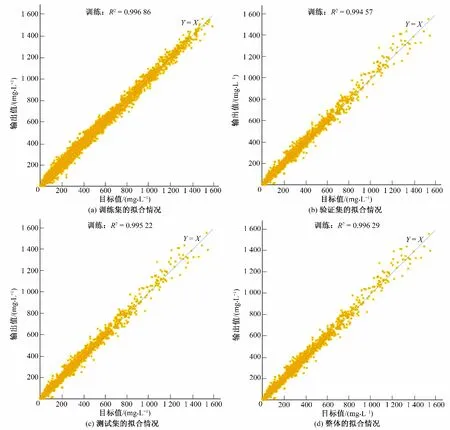
圖3 訓練集、驗證集、測試集及整體的擬合情況Fig.3 Regression of training，validation，test and all

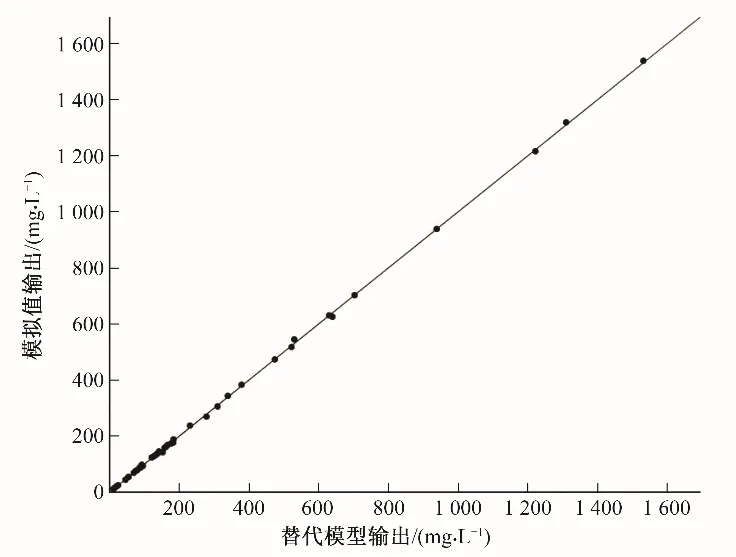
圖4 替代模型與模擬模型輸出對比Fig.4 Comparison of output between alternative model and simulation model

因此可以用BP 神經網絡建立的替代模型代替地下水溶質運移模擬模型進行運算。

2.4 優化模型建立及求解

優化模型由3 個部分組成：①待求的地下水污染源釋放歷史及場地的滲透系數作為決策變量；②各個監測井污染質濃度實際監測值與模擬計算值之差的絕對值極小化作為目標函數；③決策變量滿足地下水溶質運移規律和合理地范圍作為約束條件（替代模型作為等式約束條件）。

分別運用傳統粒子群算法和自適應權重粒子群優化算法對建立的優化模型進行求解，運用自適應權重粒子群算法時采用了自動退出迭代循環的方法，使其能夠在尋找到最優解時自動提前跳出迭代。研究最終跳出迭代循環時，迭代次數為707代，運行時間為2 分45 秒。傳統粒子群算法不能提前跳出迭代，且運行一次迭代的時間為1.5 秒，為了對比兩種算法的運行結果，同樣運行了707 代，耗時5 分54.5 秒。目標函數值收斂曲線如圖5 所示，同等條件下，傳統粒子群算法易陷入局部最優，耗時更長，而自適應權重粒子群算法的求解精度更高，耗時較短。

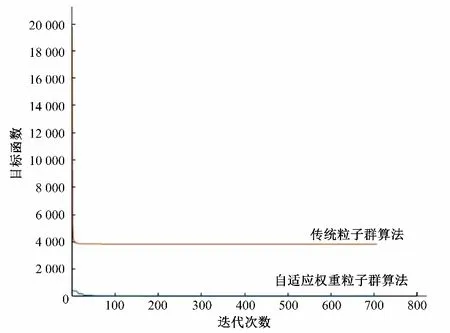
圖5 優化識別過程中目標函數值收斂曲線Fig.5 Convergence curve of objective function value

函數中的參數初始值對算法的尋優能力和計算時間有著很大的影響，因此本文運用控制變量法對函數中的參數逐一進行測試，研究發現，當粒子的數量在200 以下時，目標函數收斂曲線下降慢，計算結果精度低，容易陷入局部最優解，當粒子數量在500以上時，目標函數收斂曲線基本不變，但運算速度隨著粒子的數增加而明顯減慢；鄰域內粒子的比例越大，目標函數收斂曲線下降速度越慢，鄰域內粒子的比例越小，目標函數收斂曲線下降速度越快；慣性權重范圍、個體學習因子和社會學習因子之間相互影響。

經過反復試驗，最終確定粒子數量為500，鄰域內粒子的比例為0.5，設置個體學習因子和社會學習因子為0.8，慣性權重范圍為0.4～1.6；最大停滯迭代數為20。運用自適應權重粒子群算法求解優化模型最終得到滲透系數和污染源釋放歷史的反演結果。

由圖5、表4、5 和表6 可知，應用自適應權重優化算法求解優化模型，能夠以較快的速度搜索到全局最優，滲透系數反演結果的相對誤差均小于5%，污染源信息反演結果的相對誤差絕大多數小于5%，說明自適應權重粒子群優化算法的求解精度較高。

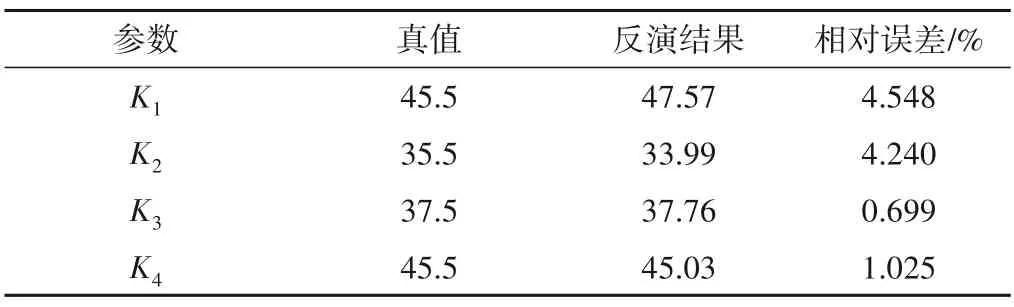
表4 滲透系數研究結果Tab.4 Experimental results of hydraulic conductivity

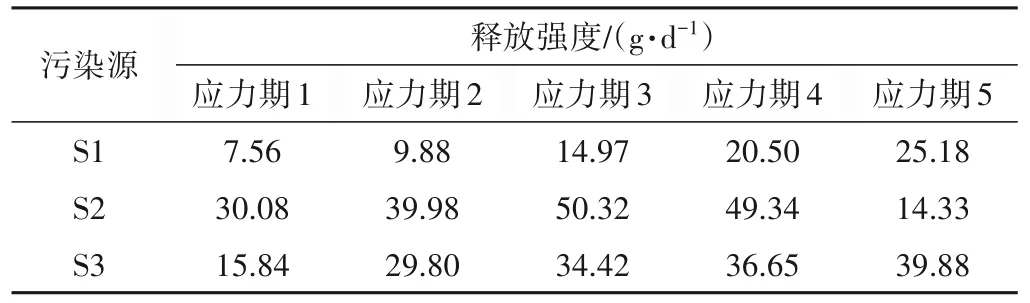
表5 污染源信息研究結果Tab.5 Experimental results of information of pollution sources

表6 污染源信息研究結果相對誤差%Tab.6 Relative error of experimental results of information of pollution sources

傳統的智能優化算法具有易于實現、運行速度快的特點，但存在收斂過程易出現停滯及收斂精度較低的缺點。自適應權重粒子群算法利用進化過程中粒子適應度的差異來評價種群的早熟收斂程度，進而動態的改變慣性權重，能夠有效避免早熟收斂問題，具有很強的局部搜索能力和全局搜索能力。

3 結論與展望

（1）運用BP 神經網絡所建立的替代模型能夠很好地近似模擬模型的輸入-輸出關系，擬合精度達到0.99，且運行速度明顯快于數值模擬模型，證明了其可以代替數值模擬模型嵌入優化模型中進行污染源溯源辨識工作。

（2）同運用傳統粒子群優化算法相比較，運用自適應權重粒子群優化算法，對優化算法的參數和迭代終止條件進行調節，可以有效地提高算法的收斂速度和計算效率，收斂得到的最優解的相對誤差基本小于5%。

（3）針對BP 神經網絡建立替代模型的權值反饋過程，研究采用的是列文伯格-馬夸爾特法調整權重和偏置使總體誤差最小，未來可以研究使用其他計算效率和收斂精度更高的優化算法來調整權重和偏置。

（4）針對優化算法參數的修改問題，研究選擇了多次試驗取經驗值的方法，在日后的研究中可以致力于尋找一種方法來減少算法收斂精度對算法參數初始值的依賴。