MONOTONICITY FORMULAS FOR PARABOLIC FREE BOUNDARY PROBLEMS ON CONES?

Chung-Kwong CHAN()Huichun ZHANG()Xiping ZHU()

Department of Mathematics,Sun Yat-sen University,Guangzhou 510275,China

E-mail:chsongg@mail2.sysu.edu.cn;zhanghc3@mail.sysu.edu.cn;stszxp@mail.sysu.edu.cn

Abstract Monotonicity formulas play a central role in the study of free boundary problems.In this note,we develop a Weiss-type monotonicity formula for solutions to parabolic free boundary problems on metric measurecones.

Key words monotonicity formula;parabolic free boundary problem;RCD-spaces

Dedicated to Professor Banghe LI on the occasion of his 80th birthday

1 Introduction

In [14],we considered free boundary problems onRCD(K,N)-spaces;this is a class of singular metric measure spaces with a generalized Riccicurvature bounded from below.The main example sincludefinited imensional Alexandrov spaces with curvature bounded from below [28,34],and the Gromov-Hausdorfflimit spaces of a family of Riemannian manifolds with Ricci curvature bounded from below uniformly and a dimension bounded from above uniformly [16,17].It is well-known that the singularities of anRCD(K,N)-space might be dense [27].We refer the readers to [6,7,25,26,30,31]and the survey [4]for the development of this generalized notion of the Riccicondition.

For a domain ? on anRCD(K,N)space(X,d, μ),the one-phase parabolic free boundary problem on ? is

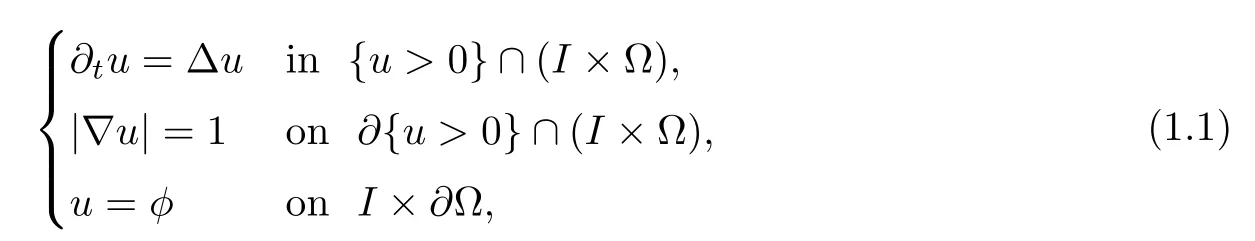
whereIis an interval,φis a given nonnegative function onI×?? ,and?{u>0}∩(I× ? )is the free boundary.

The existence of the solution to(1.1)with general given initial data is not obvious,even for the Euclidean caseX=Rn(with the Euclidean metric and the Lebesgue measure).Indeed,since the one-phase Bernoulli energy functional

is not convex,it is difficult to solve(1.1)via the gradient flow ofJ(u).The main approaches to constructing a solution of(1.1)are based on the approximations by a family of the following perturbations(see,for examples,[9,12,13,33]):

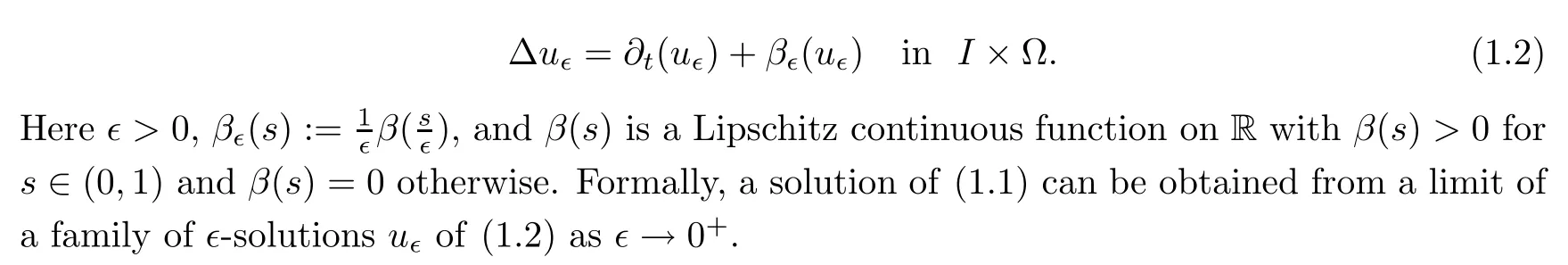
For the regularity of a solution to(1.1),and also the regularity of the free boundary,one usually performs a blow-up analysis at each point in the free boundary.Namely,one can study the limits on the tangentcone atx0,lying in the free boundary,arising from a blow-up sequence of solutions of(1.1).Since the tangentcones at almost every point in anRCD(K,N)-space areRCD(0,N)metric measurecones,it is natural to deal with the global solutions to a free boundary problem on anRCD(0,N)cone.

We now recall some notations.LetN≥2 and let(Σ,dΣ, μΣ)be a metric measure space satisfying a generalized Ricci curvature conditionRCD(N?1,N).The metric measurecone

is given byX:=CN(Σ)=[0,∞)×Σ/({0}×Σ),with the distance given by

and the measure given by

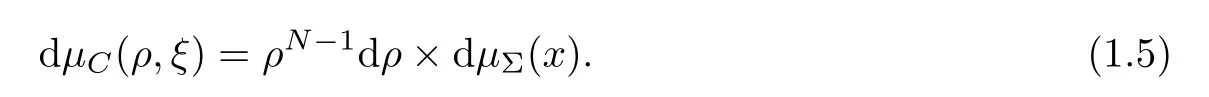
It is well known that(X,d, μ)is anRCD(0,N)-space.We refer readers to [18,23]for further propositions regrading thecones.We should mention that Allen and Chang Lara in [2]and Allen in [1]studied the free boundary problems on 2-dimensional and 3-dimensionalcones over smooth cross spaces.

Recall that the notions of the Sobolev spaceW1,2(X)on a metric measure space(X,d, μ)were introduced in [15];see also [5,10,29].SinceW1,2(X)is a Hilbert spaceon anRCD(K,N)-space,it provides the inner product RX〈?f,?g〉dμand a measure-valued Laplacian?ffor allf∈in the sense of distributions(see [19]).

Letting?>0,we consider a family of non-negative global solutions to the singular perturbation problems on theRCD(0,N)-cone(X,d, μ)=(CN(Σ),dC, μC),

whereI?R is an interval,in the sense of distributions,i.e.,

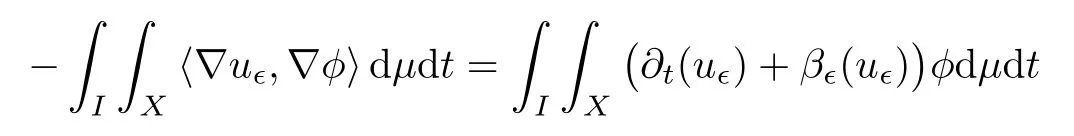
for allφ∈Lip0(I×X),where Lip0(I×X)is the space of Lipschitz continuous functions with compact support inI×X.

Monotonicity formulas play a central role in studies of free boundary problems(see [3,9,11,24,32,33]and so on).In the case whereX=Rn,the monotonicity formulas foru?and for their limitsu=as?j→0+were established by Weiss in [33].In this note,we will extend these Weiss-type monotonicity formulas to the corresponding equations on theRCD(0,N)-cone(X,d, μ)=(CN(Σ),dC, μC).

Set

Denote byothe vertex of the cone(X,d, μ)=(CN(Σ),dC, μC)and setρ(x):=dist(o,x)for any pointx=(ρ, ξ)∈X.Establish a function by

for all(s,x):=(s,ρ, ξ)∈(0,+∞)×X,and a measure on(?∞,0)×Xby

whereu?,r:=(u?)r.Here and in the sequel,for a functionv(t,x),weal ways denote there scaling withr>0 by

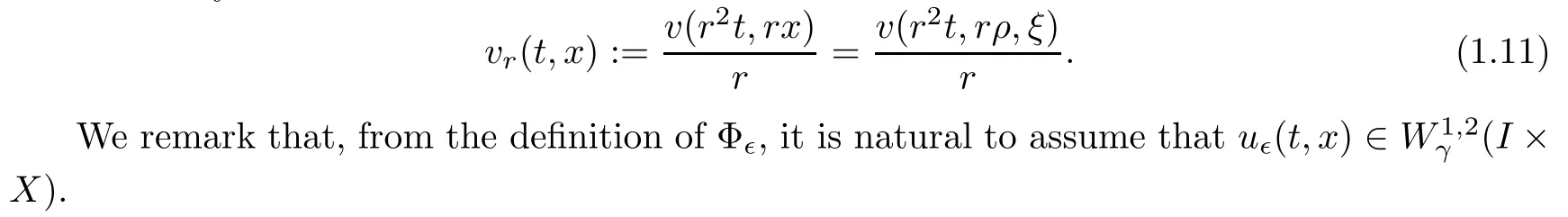
By passing to a limit as?j→0+,we will deduce a monotonicity formula for limit solutions as follows:

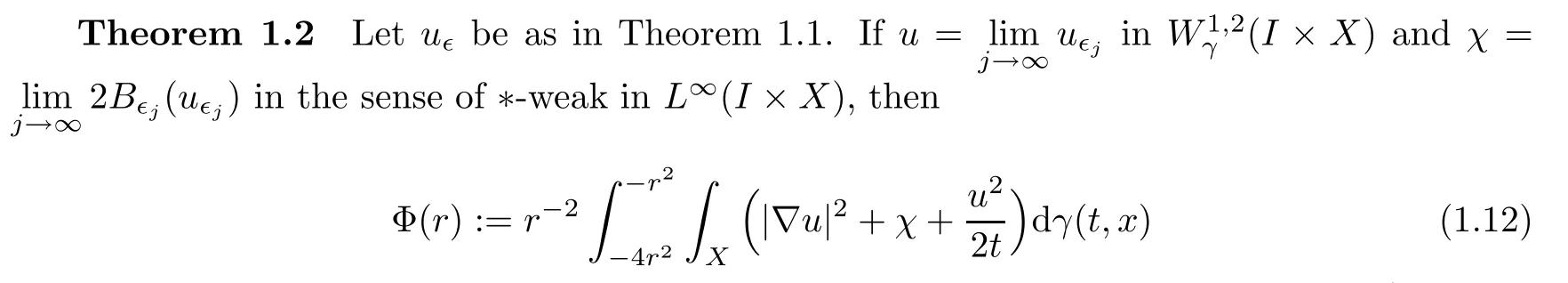
Remark 1.3One of the differences between the Rn(or the cones over smooth cross spaces,like those cones in [1,2])and the generalRCD-cones is that we are not able to assume a prioriC2-regularity and aC1/2,1-bound(uniform with respect to?)of solutions to(1.6)in the generalRCD-cones.To get the monotonicity formulas in Theorems 1.1 and 1.2,we need to pay great attention to the sometimes subtle regularity issues on generalRCD-cones.

2 Preliminaries and Notations

Let(X,d, μ)be anRCD(K,N)-space withK∈R,N∈[2,+∞).We recall the notion of Sobolev spaces;see [5,6,15,21,29].Given a continuous functionfonX,the point wise Lipschitz constant [15]offatxis defined by

It is clear that Lipfisμ-measurable.Let ? ?Xbe an open domain and let 1≤p<+∞.TheW1,p-norm of a locally Lipschitz functionf∈Liploc( ? )on ? is defined by

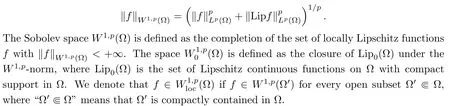
For anyf∈W1,p( ? )wherep∈(1,∞),it is well-known that there is a function|?f|∈Lp( ? ),the so-called generalized minimal upper gradient,such that

Since(X,d, μ)is anRCD(K,N)-space,the spaceW1,2( ? )is a Hilbert space.It was shown in [19,Sect.4]that,for anyf,g∈W1,2( ? ),the limit

exists inL1( ? ).Moreover,this inner product〈?f,?g〉is bi-linear,and satisfies Cauchy-Schwarz inequality,the Chain rule and the Leibniz rule(see [19,Sect.4]).

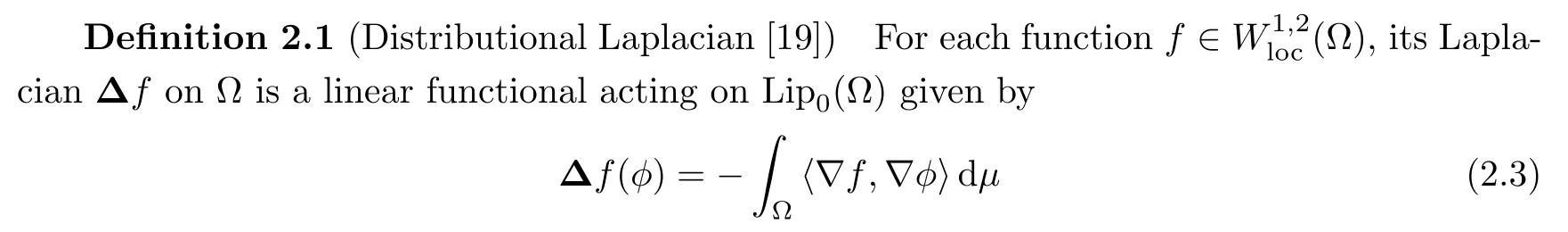
for allφ∈Lip0( ? ).If there is a signed Radon measureνsuch that?f(φ)=R?φdνfor allφ∈Lip0( ? ),then we say that?f=νon ? in the sense of distributions.

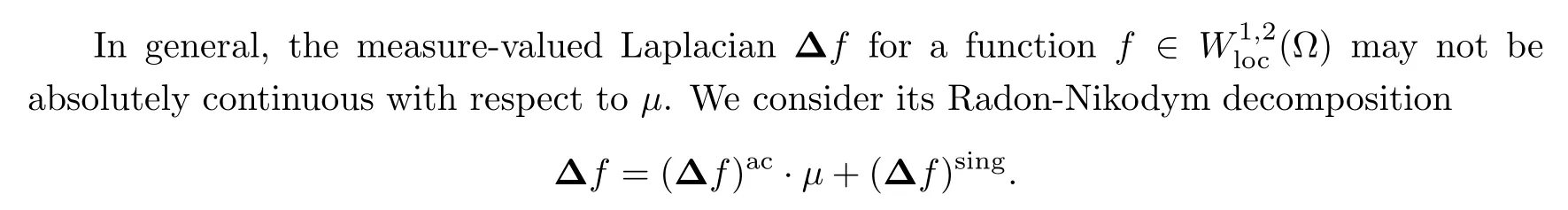
This Laplacian on ? is linear,and it satisfies the Chain rule,and the Leibniz rule [19].

When ? =X,the inner product(2.2)provides a Dirichlet form E(f,g):=RX〈?f,?g〉dμonX.This Dirichlet form(E,W1,2(X))has an infinitesimal generator?Ewith domainD(?E)?W1,2(X),i.e.,

It has been shown [19]that iff∈W1,2(X)andg∈L2(X),then

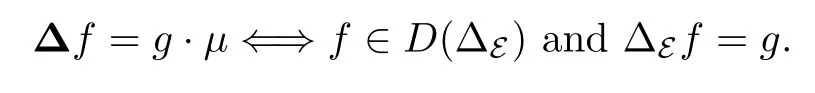
We need the following regularity result for Poisson equations:

see,for instance,[8]for the existence of such a cut-offfunction.By the Leibniz rule for the measured-value Laplacian(see [19,Sect.4]),we have that

ProofTake any functionφ(t,x)∈Lip0(I× ? ).Then,for eacht∈I,the functionφ(t,·)is in Lip0( ? ).For almost allt∈I,since the functionw(t,·)is a solution to the Poisson equation(2.7)on ? ,we have that

Now the desired result follows from the Fubini Theorem. □

We refer readers to [20]for more properties of Sobolev spaces on product spaces.

From this point forward,we always assume that(X,d, μ)=(CN(Σ),dC, μC)is anRCD(0,N)-cone withN≥2.

Recall thatρ(x)=dist(o,x)for any pointx=(ρ, ξ)∈X,whereξ∈Σ andρ=ρ(x).It is easy to check that

and hence that

whereGis given by(1.7).

3 The Proofs of Theorem 1.1 and Theorem 1.2

wherewris given by(1.11).

ProofSinceG(?t,x)is bounded onI×X,the function

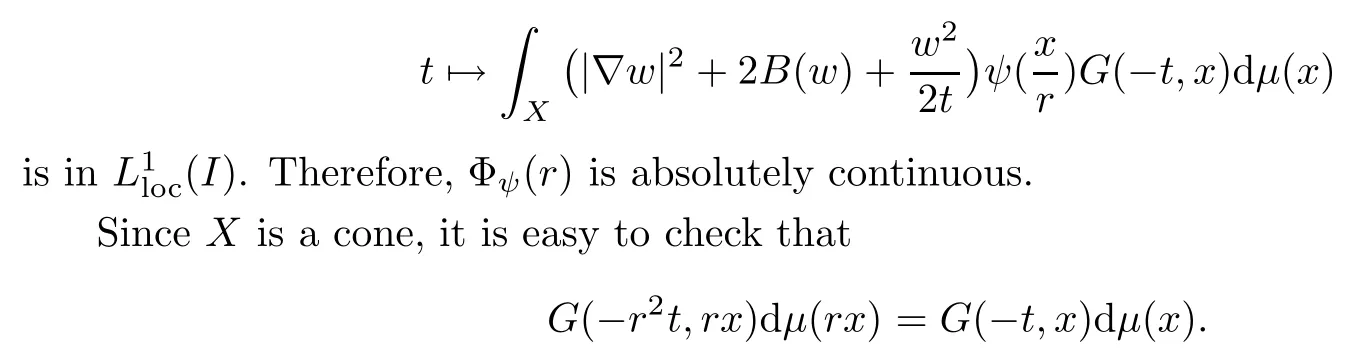
Hence,we can rewrite Φψ(r)as

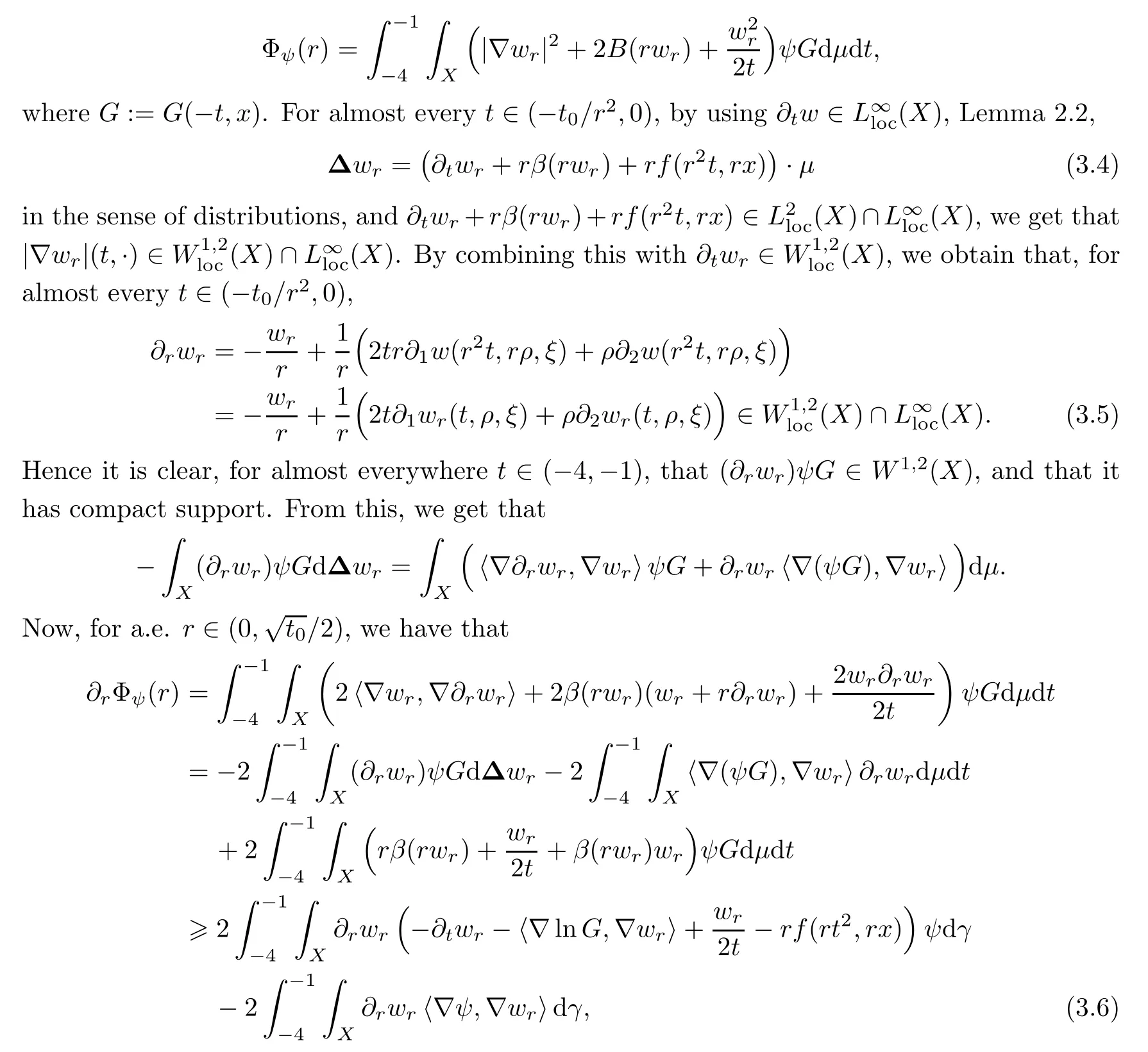
where we have used(3.4),the fact thatβ(rwr)wr≥0,and the Leibniz rule for the inner product〈?lnG,?wr〉(by [19,Sect.4]).By combining(3.5),(3.6),and

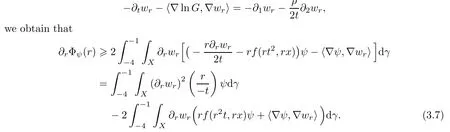
This,by the Cauchy-Schwarz inequality,implies the desired estimate,and hence the proof is finished. □

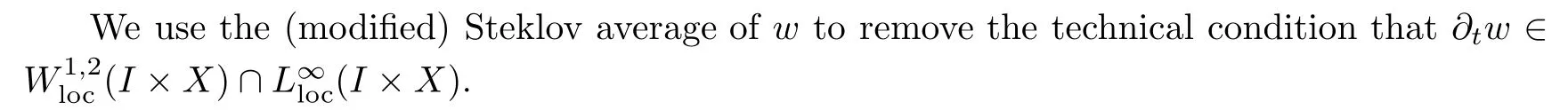
Now we are in position to prove Theorem 1.1.

Now we present the proof of Theorem 1.2.