齊次多項式正定性的新判定準則

趙鵬程,王 峰

(貴州民族大學 數據科學與信息工程學院,貴州 貴陽 550025)

結構張量在圖像處理、醫學降噪和彈性摩擦等問題中有著重要應用價值.[1-4]尤其是H-張量,因其在數值分析上的重要作用,其理論、性質及迭代算法受到眾多學者的廣泛研究.[5-10]同時,多元偶次齊次多項式在諸多問題中有著廣泛的應用,[11-18]其正定性的判定受到越來越多的關注.本文借助H-張量來判定齊次多項式的正定性,并用數值算例表明了所得結論的有效性．

1 預備知識

用R(C)表示實(復)數集,N=[n]={1,2,…,n} .m階n維實(復)張量A=(ai1i2…im)由nm個實(復)元素構成,其中ai1i2…im∈R(C),ij∈N,j∈[m].對m階n維張量A=(ai1i2…im),若存在數λ和非零向量x=(x1,x2,…,xn)T∈Cn,使得Axm-1=λx[m-1],則稱λ為A的特征值,x為對應于λ的特征向量,其中Axm-1和x[m-1]的第i個分量分別是:

若ai1i2…im=aπ(i1i2…im),?π∈Πm,則稱A=(ai1i2…im)是對稱的,其中Πm為m個指標的置換群.稱I=(δi1i2…im)為單位張量,其中:

設f(x)是一個m階n次齊次多項式,其中:

若對:

則稱f(x)是正定的.f(x)可表示為m階n維對稱張量A與xm的乘積,[1]如:

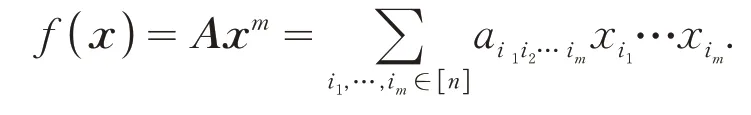
當f(x)是正定時,對稱張量A也是正定的.

定義1[7]設A=(ai1i2…im)是m階n維張量,若存在正向量x=(x1,x2,…,xn)T∈Rn,使得:

則稱A是H-張量.

定義2[4]設A=(ai1i2…im)是一個m階n維張量,若存在非空子集I ?N,使得:

則稱A是可約的.否則,稱A是不可約的.

定義3[8]設A=(ai1i2…im)是一個m階n維張量,若存在指標k1,k2,…,kr,使得:

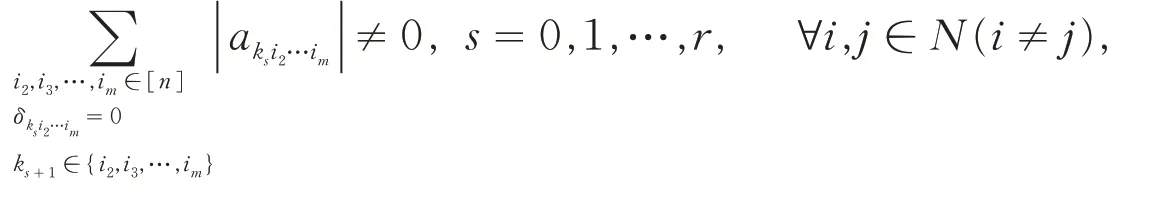
其中k0=i,kr+1=j,則稱A中有一條從i到j的非零元素鏈.

引理1[5]若A=(ai1i2…im)是嚴格對角占優的,則A是H-張量.

引理2[9]設A=(ai1i2…im)是m階n維張量.如果存在正對角矩陣X,使得AXm-1是H-張量,則A是H-張量.

引理3[5]設A=(ai1i2…im)是m階n維張量且不可約.若:

且至少有一個嚴格不等式成立,則A是H-張量.

引理4[8]設A=(ai1i2…im)是m階n維張量.若:

(i)|aii…i|≥ri(A), ?i∈N;

(ii)N3={i∈N:|aii…i|>ri(A)}≠?;

(iii)?i?N3,從i到j存在一個非零元素鏈,使得j∈N3;

則A是H-張量.

2 主要……

登錄APP查看全文

猜你喜歡

定義

活用定義巧解統計概率解答題

中學生數理化(高中版.高考數學)(2021年3期)2021-06-09 06:09:14

例談橢圓的定義及其應用

中學生數理化(高中版.高二數學)(2021年12期)2021-04-26 07:43:38

題在書外 根在書中——圓錐曲線第三定義在教材和高考中的滲透

中學生數理化(高中版.高二數學)(2021年2期)2021-03-19 08:54:04

永遠不要用“起點”定義自己

海峽姐妹(2020年9期)2021-01-04 01:35:44

嚴昊：不定義終點 一直在路上

華人時刊(2020年13期)2020-09-25 08:21:32

定義“風格”

VOGUE服飾與美容(2020年9期)2020-09-02 14:47:26

成功的定義

山東青年(2016年1期)2016-02-28 14:25:25

有壹手——重新定義快修連鎖

汽車維護與修理(2015年6期)2015-02-28 12:16:55

修辭學的重大定義

當代修辭學(2014年3期)2014-01-21 02:30:44

山的定義

公務員文萃(2013年5期)2013-03-11 16:08:37

四川文理學院學報 2022年5期

四川文理學院學報的其它文章

高校課程管理:內容·主體·路徑

悖論困境下青少年“勞動認同”培育探析

簡論傳統創業創新思想的精神內涵及時代特色

新時代高校統一戰線意識形態安全路徑研究

新時代提升地方高校民主黨派基層支部“組織活力”研究
——以四川文理學院為例

章繼肅先生詩詞作品的美學特征及社會功能