慣性積對光電設備減振性能的影響

張澤清， 姜偉偉， 賀壁， 扈宏毅， 劉磊

(1.中國科學院光電技術研究所， 成都 610209； 2.中國科學院光束控制重點實驗室， 成都 610209； 3.中國科學院大學光電學院， 北京 100049)

隨著科學技術的發展，光電設備由地基式發展到車載、艦載、機載及星載等機動平臺承載式。在機動平臺上，由于工作環境存在著高帶寬大幅值的隨機振動，載體的振動會通過平臺傳遞到光學系統上，造成光學系統振動，這些振動的存在會影響成像系統的成像質量。那么對光電設備進行振動隔離十分必要，被動減振系統結構簡單，可靠性高，經濟性好，成為光電設備主要的減振方式[1-2]。

振動可以分為線振動與角振動，國內外很多學者已經對振動對成像質量的影響作了大量分析。趙鵬等[3]、耿文豹等[4]、李玉龍等[5]研究指出角振動對光電系統的影響遠遠大于線振動的影響。為了降低角振動響應，通常在對光電設備進行減振設計時綜合考慮質量和慣量，減振器的安裝位置及剛度、阻尼參數，以設計解耦度高的系統。理想情況下，單層隔振系統要實現完全解耦，要求各彈性主軸與各慣性主軸完全重合。但是在實際工程中，光電設備的質量分布不均且外形不規則，這樣光電設備減振系統不僅存在彈性耦合還存在慣性耦合。李曉波等[6]通過正弦掃頻實驗對比了捷聯慣導減振系統有無偏心情況下的響應，指出偏心引起了系統振動的耦合，得到減振器需要對稱安裝避免偏心的結論；劉勇等[7]通過模態分析、諧響應分析和隨機響應分析研究了偏心減振系統的動力學特性、頻響特性和隨機響應特性；付繼波等[8]從理論和數值仿真兩方面證明了系統偏心造成了線振動和角振動的耦合，并進一步證明了偏心量的增大造成角振動頻率降低，線振動頻率增加；孫玉華等[9]分析了質心偏移對減振系統固有頻率和解耦率的影響，指出減振器安裝跨距最短的方向系統頻率和解耦率受質心偏移影響最為明顯；Okwudire等[10]建立了二自由度減振系統，理論上證明了質心偏移造成了線振動和角振動耦合，導致系統的一階頻率降低，二階頻率增加。

上述研究均假設質量矩陣為對角矩陣，未考慮設備慣性積不為零對減振系統動力學特性和幅頻響應特性的影響。針對慣性積導致光電設備減振系統角振動耦合的問題，建立減振系統的數學模型，分析了慣性積造成的不同耦合形式，并推導了固有頻率的無量綱化公式，利用數值計算方法，研究慣性積對系統動力學特性以及幅頻響應的影響，為光電設備質量分布的優化工作提供理論依據。

1 減振模型與動力學微分方程

光電設備通過被動減振器與載體柔性連接，由于光電設備的一階頻率一般遠遠高于減振器的固有頻率，可將光電設備作為剛體處理。一般而言，被動減振的動力學是非線性的[11-12]。但是對于微小位移的振動，近似為線性模型能夠滿足工程需要[11]。那么，光電設備減振系統動力學模型可以近似為圖1所示的六自由度等效模型。

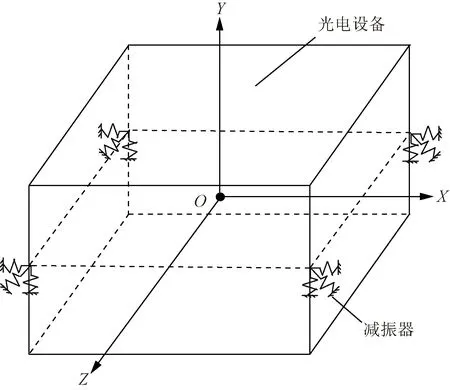
圖1 減振系統六自由度模型Fig.1 6-DOF model of the vibration isolation system

為了方便推導動力學方程及分析動力學特性，首先明確彈性中心這個概念。減振器可以看為有兩固連端的三維彈性支承，如果沿著某軸線的載荷作用在彈性支撐上，使得彈性支承兩端的移動方向和力方向保持一致，并且兩端之間只有線位移沒有角位移，那么這個軸線稱為彈性支承的彈性主軸[13]。當一個彈性支承和剛體組成系統，彈性支承的三個彈性主軸的交點為彈性中心；當多個彈性支承和剛體組成系統時，多個彈性支承的三個方向的彈性主軸交于一點時，該點為彈性中心[14]。

定義彈性坐標系、慣性坐標系和求解坐標系。彈性坐標系原點位于減振系統彈性中心，各坐標軸與彈性主軸重合，與圖1中所示坐標系各軸一致；慣性坐標系原點位于設備質心，各坐標軸分別對應設備的各個中心慣性主軸。求解坐標系原點為光電設備質心，三個坐標軸與彈性坐標系各軸一致。

在小位移假設的條件下，阻尼對于系統固有頻率的影響很小可以忽略不計，推導出減振系統的六自由度無阻尼自由振動動力學方程，寫為

(1)

式(1)可以簡寫為

(2)

式(2)中:矩陣M、K分別稱為系統的質量矩陣和剛度矩陣，可代入系統的特征方程，即

|K-w2M|=0

(3)

式(3)中：w表示系統的固有頻率，計算得到系統的六階固有頻率[15]。

假設光電設備為質量分布均勻的長方體，當減振器安裝面通過質心并關于質心對稱分布時，減振系統的彈性中心與質心重合，即求解坐標系與彈性坐標系一致。此時有kxβ=kβx=kxγ=kγx=kyγ=kγy=0；kαβ=kβα=kαγ=kγα=kβγ=kγβ=0。

在此前提下，可以分為3種情況分別談論。

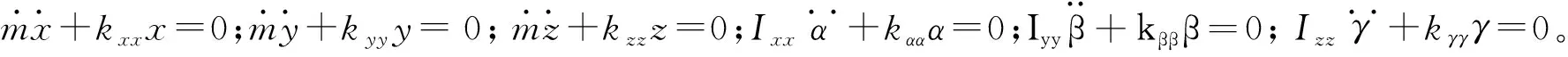
(2) 彈性坐標系與慣性坐標系Z軸重合，其他兩軸不重合的情況下(其他情況類似)，此時有Ixz=Izx=Iyz=Izy=0；Ixy=Iyx≠0。

系統α與β方向通過慣性積Ixy耦合，其余方向獨立。由于本文目的研究慣性積參數對耦合減振系統的影響，只討論耦合的兩個角方向，方程可以簡化為

(4)

(3) 彈性坐標系與慣性坐標系的各個坐標軸都不平行，此時有Ixz=Izx=Iyz=Izy=0；Ixy=Iyx≠0，Ixz=Izx≠0，Iyz=Izy≠0。

系統α、β和γ三個角方向相互耦合，其余方向獨立，耦合的三個角方向的方程為

(5)

2 慣性積對固有頻率的影響

對上述第2種情況進行深入分析，對式(2)求解，得到系統的無阻尼固有頻率并進行無量綱化處理[10]，即

(6)

當ε取不同值時，分別畫出無量綱固有頻率關于無量綱慣性積的曲線，如圖2所示。下面分ε≠1和ε=1兩種情況進行討論。

圖2 無量綱慣性積對無量綱固有頻率的影響Fig.2 Influence of dimensionless inertia product on dimensionless natural frequency

3 算例分析

某光電設備減振系統關于XOY平面對稱，分別對圖3所示三種系統進行討論。

圖3 減振系統平面示意圖Fig.3 Simplified plane diagram of vibration isolation system

三種系統保持質量相同，質心一致，其慣性參數以及計算的無量綱慣性積列于表1。

表1 各系統的慣性參數Table 1 Inertial parameters of each system

減振器安裝方式及位置如圖1所示，關于質心對稱安裝，減振器另一端與工裝件相連；四個減振器參數相同，三向等剛度，設置剛度k=1 250 N/m，設置阻尼比為0.12，減振器安裝位置參數表2所示。

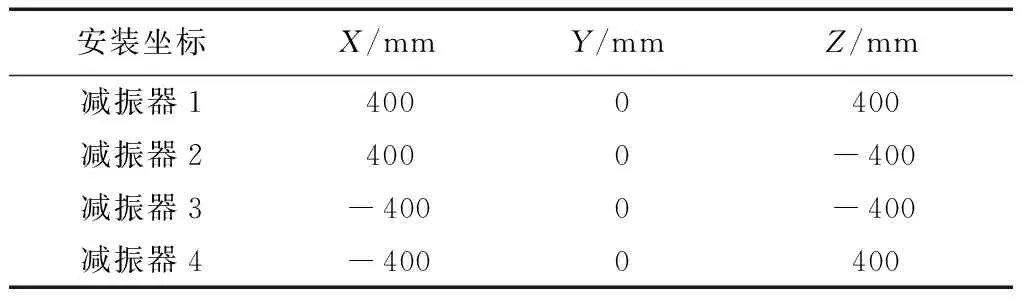
表2 減振器安裝坐標Table 2 Inertia coordinate of each isolators

根據式(2)計算出系統的固有頻率，為方便分析，將3種系統計算得到的模態頻率以及各自的無量綱慣性積列于表3，并計算兩階頻率的差值。

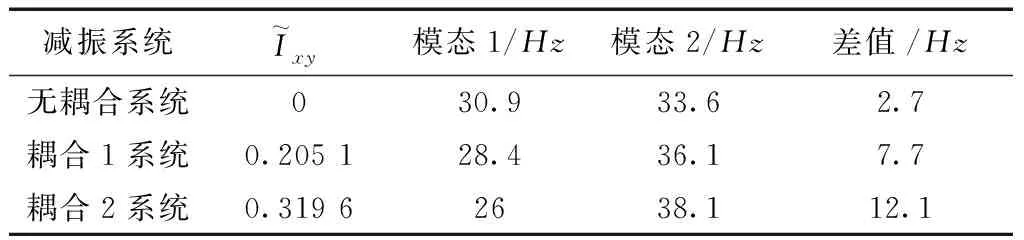
表3 系統固有頻率分布Table 3 Distribution of system natural frequency

減振系統的性能常用傳遞率來表示。對于耦合系統，定義角位移激勵下的位移傳遞率，表達式為

(7)

式(7)中：x為在α或者β方向產生的響應；y為激勵在α或者β方向產生的靜態響應。

對工裝件分別施加兩個角方向的位移正弦激勵，幅值為1，頻率范圍為0～100 Hz。利用數值計算方法，得到的系統的傳遞率如圖4所示。

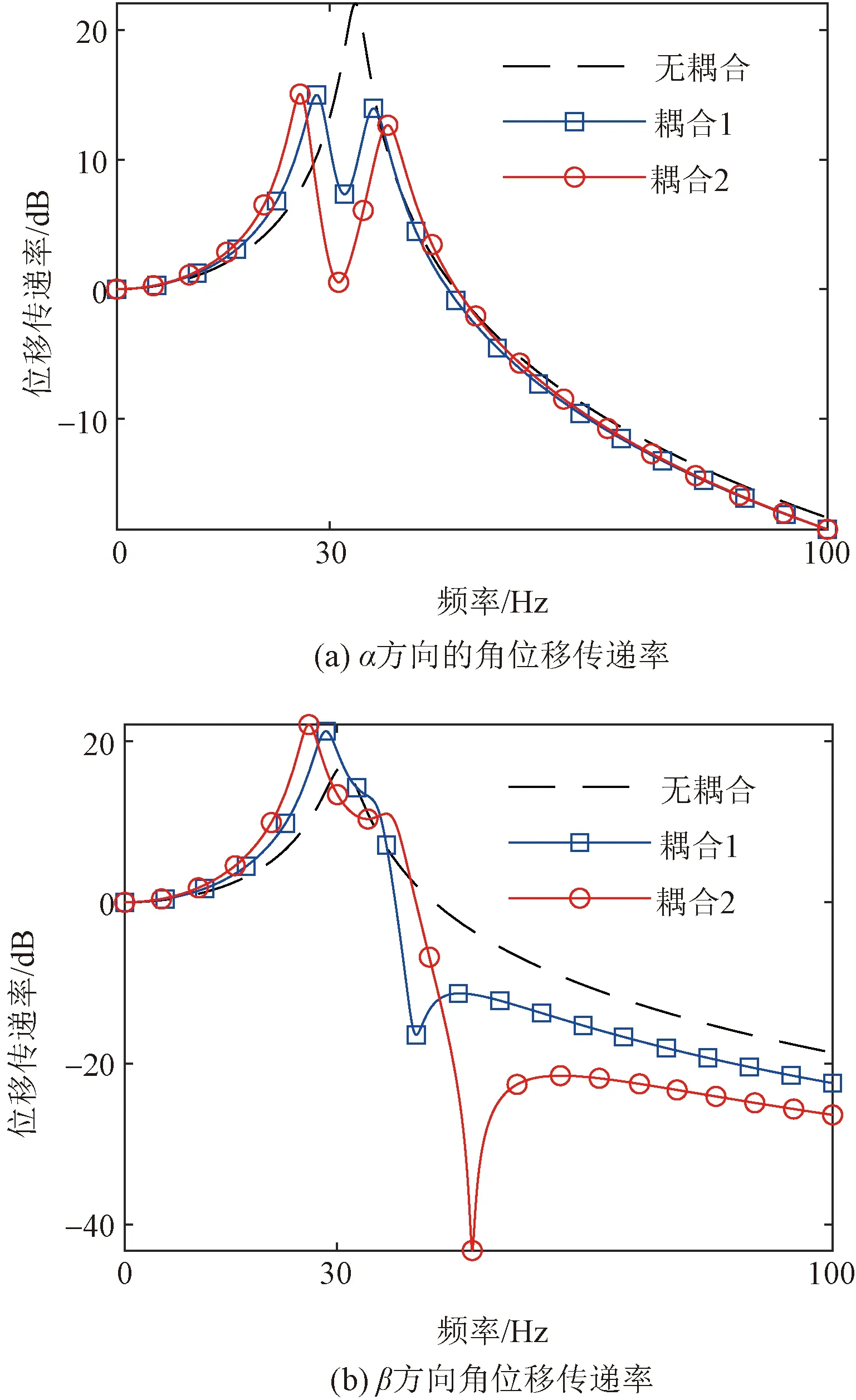
圖4 各系統兩個角方向的位移傳遞率Fig.4 Displacement transmissibility in the two angular directions of each system

與無耦合系統相比，耦合系統在兩個轉動方向均出現峰值，因為慣性積的存在，任一方向的激勵均會在兩個方向上產生響應。耦合系統有兩個共振峰，一個反共振峰，這是區別無耦合系統的重要特征。

4 結論

本文建立了慣性積不為零的光電設備減振系統動力學模型，對僅存在慣性耦合的減振系統進行了理論及數值分析，推導了系統固有頻率與慣性積參數的數學表達公式，研究了系統動力學特性和幅頻響應特性。在某型直升機載光電跟蹤吊艙設備中，根據直升機實際測量的激勵幅值，依據上述理論設計合適的設備慣性積分布，得到跟蹤精度0.5 mrad(均方根)的結果，圓滿完成了試驗任務，得到如下結論。

(1) 慣性積的存在改變了系統動力學特性，引起對應兩個角方向的耦合，降低了低階固有頻率，增大了高階固有頻率。

(2) 隨慣性積的增加，系統對應的兩階固有頻率差值增大。減振系統耦合的兩個方向的固有頻率一定不相等。

(3) 針對光電設備視軸穩定，在設備存在角振動激勵時，為光電設備減振系統各階的模態頻率的設計以及優化設備慣性積分布提供了理論依據。

(4) 當對兩個角方向同時激勵時，相較于無耦合系統，慣性耦合系統在低階模態方向的減振區傳遞率小于無耦合系統。