變截面箱梁橋懸臂施工過程剪力滯效應

陳建民， 駱維斌*， 冀偉

(1.公路建設與養護技術材料及裝配交通運輸行業研發中心， 蘭州 730030； 2.蘭州交通大學土木學院， 蘭州 730070)

變截面預應力混凝土連續箱梁橋因其抗彎抗扭剛度大、濕接縫少和外形簡潔美觀等優點，在現代橋梁建設中得到廣泛使用。剪力滯效應是在梁受彎時由于翼緣板的剪切變形不均勻而造成的彎曲正應力沿梁寬方向分布不均勻的現象[1]。國內外學者對剪力滯效應開展了大量的研究，王連廣等[2]在研究鋼-混凝土組合箱梁剪力滯效應時，利用變分原理推導了典型的簡支組合箱梁在跨中集中荷載作用下的解析解；江林松等[3]在對比分析了中外典型規范對鋼-混組合連續直梁橋有效寬度計算結果的基礎上，基于數值模擬，研究了小半徑雙工字鋼-混組合連續彎梁橋的剪力滯效應和有效寬度，提出有限寬度的簡化計算方法；周茂定等[4]對薄壁箱梁的剪力滯翹曲位移函數進行了修正，研究了箱梁高寬比、寬跨比、板寬比等參數對剪力滯的影響；趙志峰等[5]基于比擬桿法，研究了單箱三室薄壁箱梁分別在集中荷載作用和均布荷載作用下的剪力滯效應；Boules[6]通過有限元模擬，研究了U形梁的翹曲變形和剪力滯效應；舒小娟等[7]在綜合考慮全截面剪切應變能的基礎上，利用能量變分原理建立了剪滯位移的彎曲剪力滯控制微分方程組；朱力等[8]提出了一種考慮滑移時，求解鋼-混凝土組合箱型梁剪力滯效應的理論模型；衛星等[9]研究了單箱雙室波形鋼腹板PC組合梁的剪力滯效應；劉洋等[10]以蘭州河口大橋為工程背景，研究了后續施工以及施工工況變化對已完成梁段剪力滯效應影響；王旭飛等[11]利用能量變分原理和有限元，研究了雙線混凝土U形梁的剪力滯效應；Kraus[12]研究了梁彎曲應力受剪力滯效應影響程度大小及規律；潘旦光等[13]以等截面Euler梁的自由振動模態為Ritz基函數，研究了變高度箱梁的剪力滯效應；周聰等[14]利用比擬桿法研究了變截面波形鋼腹板組合箱梁的剪力滯效應；鄧德員等[15]利用比擬桿法對箱形截面的剪力滯效應進行分析，推導承受集中荷載和均布荷載的簡支梁考慮剪力滯效應的正應力計算公式。

然而，對連續箱梁懸臂施工階段剪力滯效應研究較為匱乏，現以某新建(48+80+48) m預應力混凝土連續梁橋為背景，研究變截面預應力混凝土連續箱梁橋在懸臂施工階段的剪力滯效應及其變化規律。所采用試驗研究方法及成果可為同類橋梁的剪力滯分析提供參考。

1 剪力滯效應理論

初等梁理論中的平截面假定，是指在對稱荷載作用下，假定箱梁具有無限抗剪剛度，從而沿梁寬方向產生的彎曲正應力是均勻分布的。而實際的箱梁在荷載作用下產生的彎曲橫向力是通過腹板傳給翼板，由于剪應力在翼板上的分布是不均勻的，因此剪切變形沿翼板分布也是不均勻的，就引起了翼板的縱向位移隨遠離腹板距離的增大而滯后，最后造成彎曲正應力在橫向分布呈不均勻分布，這種現象稱之為剪力滯后效應。剪力滯根據其規律有正剪力滯和負剪力滯之分，其定義為：腹板與翼板交界處的正應力大于按初等梁彎曲理論計算得到的應力值時為正，反之為負[16]，應力分布如圖1所示。

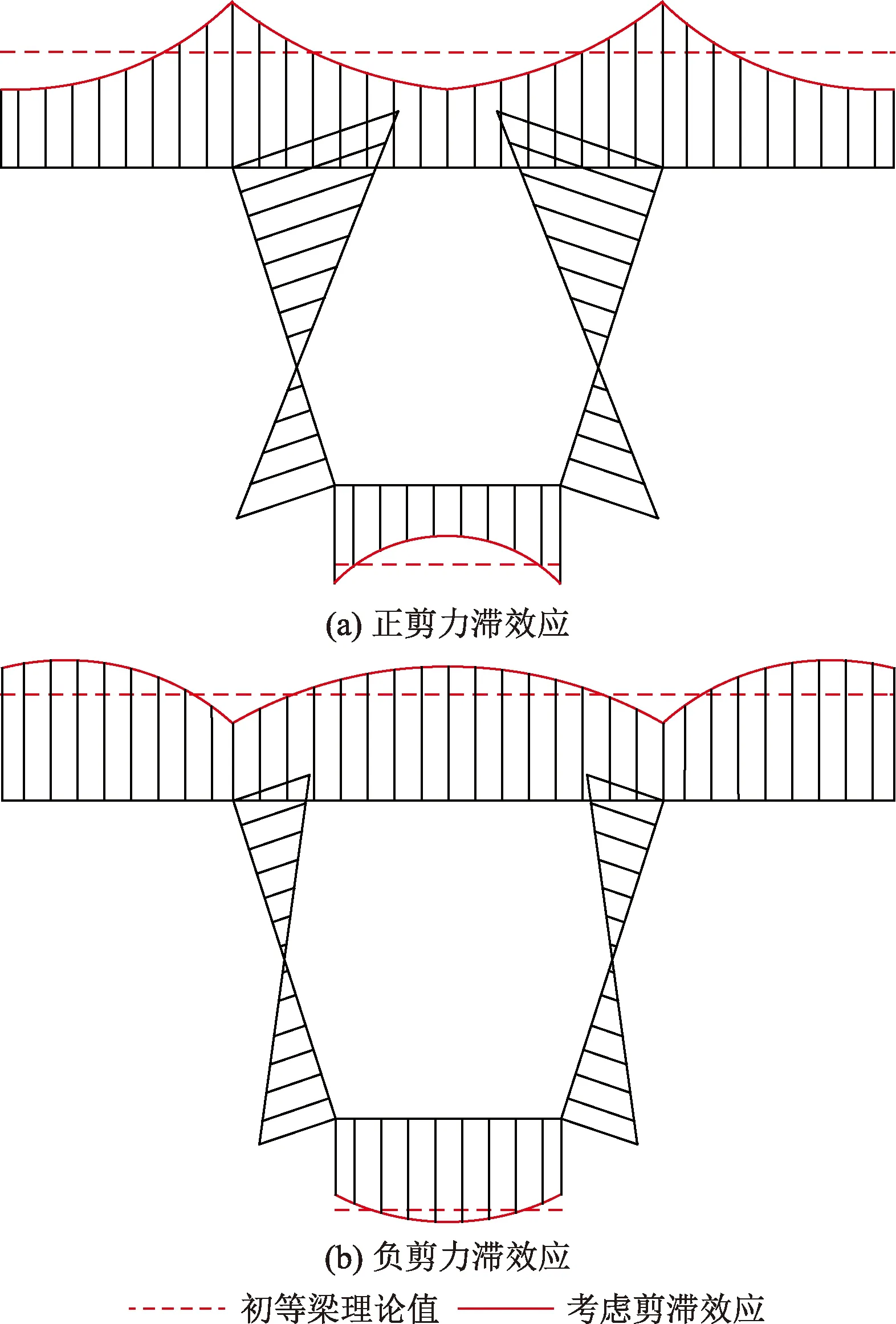
圖1 箱梁剪力滯效應Fig.1 Shear lag effect of box girder

1.1 剪力滯控制微分方程及邊界條件

對于變截面箱梁剪力滯的求解，文獻[17]中得到的剪力滯基本微分方程為

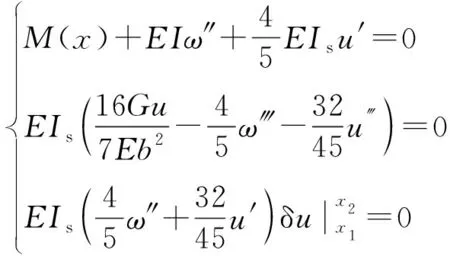
(1)

式(1)中:M(x)為梁體彎矩；E為混凝土彈性模量；I為箱梁截面慣性矩；ω為梁體豎向撓度；u為梁體縱向位移；G混凝土剪切模量；Is為翼板慣性矩；b為翼板寬度一半。

在求解變截面箱梁剪力滯時，其截面慣性矩為x的函數，此時箱梁慣性矩和翼板慣性矩可表示為I(x)和Is(x)，將式(1)經過整理，可以得到變截面箱梁剪力滯的微分方程為

(2)

在變截面箱梁中，α(x)沿梁縱向的變化小，因此α(x)的一階導數幾乎為零，進一步造成參數m的值特別小，一般可忽略不計，此時變截面箱梁剪力滯的控制微分方程為

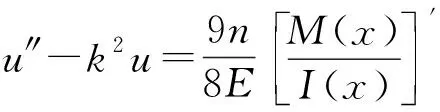
(3)

可進一步求得變截面箱梁翼板位置的剪力滯方程。

翼板和腹板交界位置的剪力滯方程為

(4)

翼板中心位置的剪力滯方程為

(5)

式中：σi表示考慮剪滯效應的變截面箱梁翼板與腹板交界位置的縱向正應力；σc表示考慮剪滯效應的變截面箱梁翼板中心位置的縱向正應力；σ表示按初等梁理論求解的箱梁縱向正應力。

1.2 差分法求解剪力滯系數

對于式(3)變截面箱梁剪力滯控制微分方程的求解，鑒于其方程中系數是變化的，可采用差分原理進行近似求解，差分分格如圖2所示。

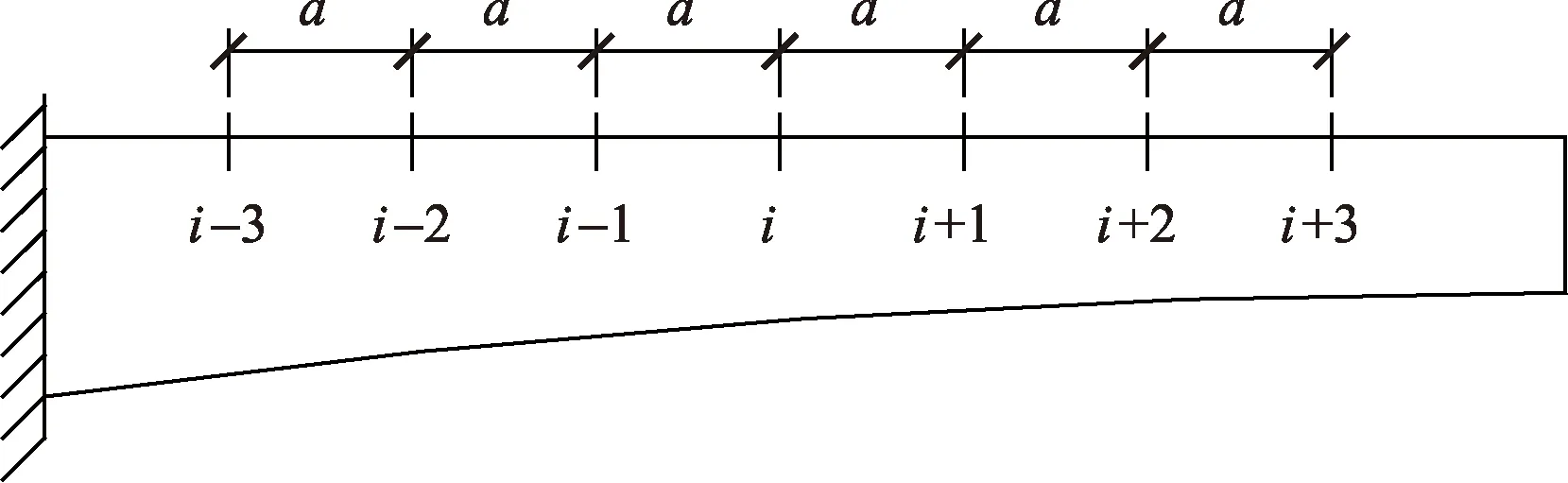
a表示一個步長圖2 變截面箱梁差分分格Fig.2 The difference scheme of variable cross-section cantilever girder

取第i點為研究對象，第一階和第二階差分方程為

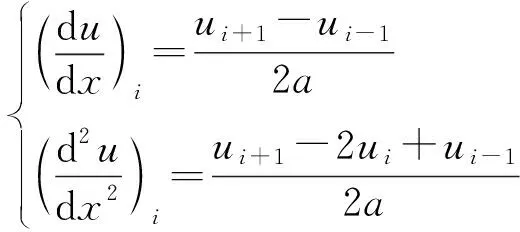
(6)

將式(6)代入式(3)可得變截面箱梁剪力滯控制微分方程的差分表示為

(7)

同理可求得邊界條件的差分表示為

(8)

根據懸臂梁邊界條件，可以進一步求得施工過程中變截面箱梁剪力滯的求解公式為

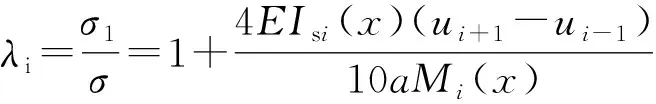
(9)

(10)

1.3 求解差分方程

為了保證計算結果的具有相當精度的同時，計算過程又不會很煩瑣，因此取4個步距，每個步距長度為a，總共有5個節點(按1～5進行編號)，將每一個節點參數代入到式(7)的差分方程中可得到5個節點差分方程，用矩形的形式表示為

Gu=Q

(11)

式(11)中：G為系數矩陣；u為位移矩陣；Q為荷載矩陣。具體表示為

(12)

G=[u1,u2,…，u5]

(13)

(14)

2 算例分析

2.1 工程概況

以某新建(48+80+48) m預應力混凝土連續梁橋為研究背景，該橋截面采用單箱單室、變截面箱形截面，橋跨布置如圖3所示。

圖3 連續梁橋跨布置Fig.3 Layout drawing of the continuous girder

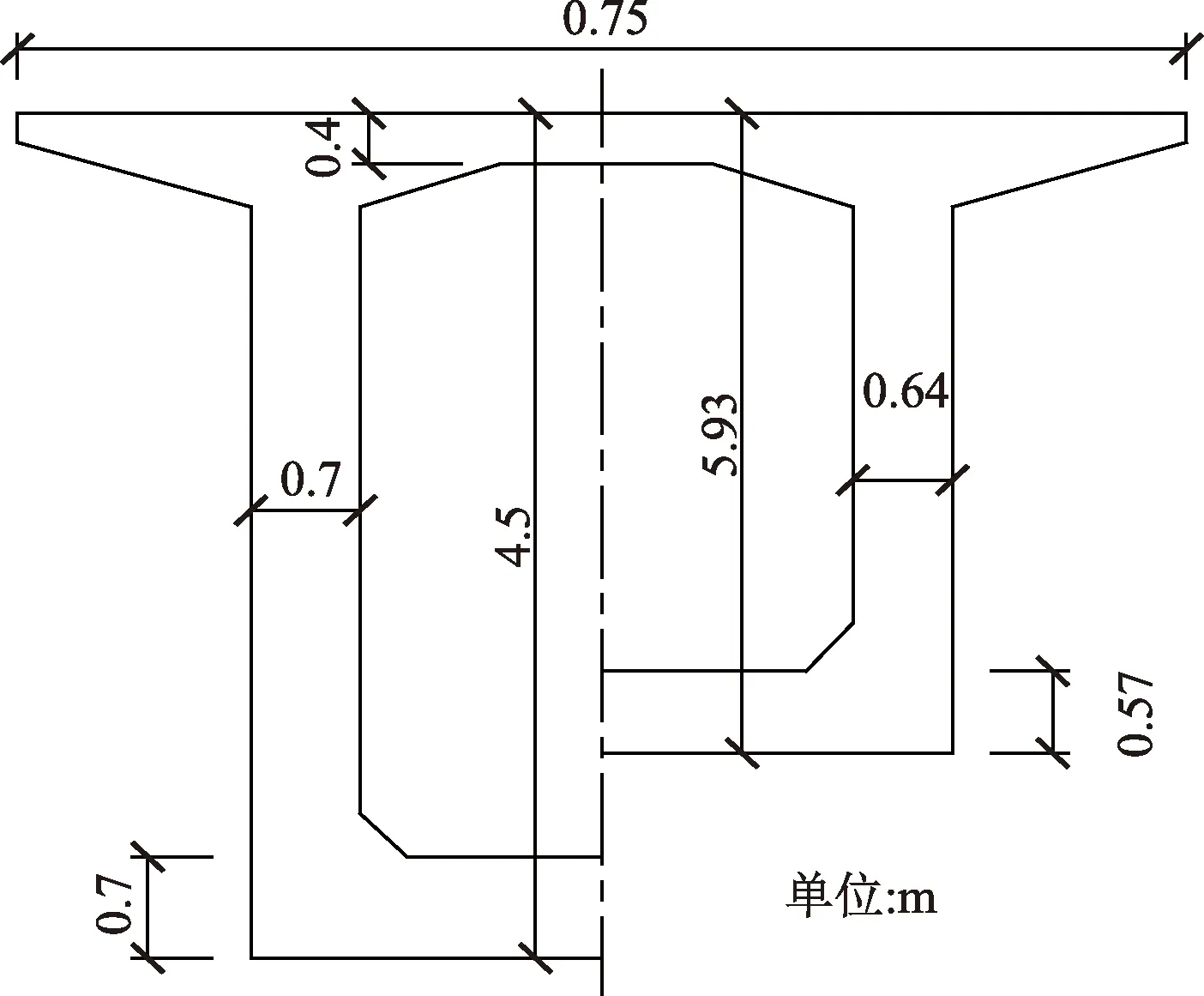
圖4 箱梁斷面Fig.4 Section diagram of box girder

連續梁掛籃懸臂澆筑施工分為9個梁段，梁段長度布置為(4×3.5+5×4.0) m，現取前4個梁段進行剪力滯系數的研究。1～4號塊的梁斷面尺寸為：頂板寬7.50 m，頂板厚0.4 m，底板寬4.50 m；梁高、腹板厚和底板厚均按二次拋物線設置成變截面，梁高從5.93 m漸變至4.5 m，底板從0.7 m漸變至0.57 m；腹板由0.7 m漸變至0.6 m，梁橫斷面如圖4所示。

箱梁梁體選用C50混凝土；縱向預應力鋼束采用直徑為15.2 mm的鋼絞線，鋼束抗拉強度標準值為1 860 MPa，鋼束采用雙端張拉；豎向預應力鋼筋采用Φ16-2無黏結預應力鋼棒。

2.2 變截面箱梁剪力滯求解

從1號梁塊到4號梁塊合計5個截面，各截面的尺寸以及計算到各截面的慣性矩如表1所示。

表1 箱梁斷面尺寸參數Table 1 Section dimension of the box girder

根據以上理論公式，求得系數矩陣G的各項參數，結果如表2所示。

表2 系數矩陣計算Table 2 Calculation of the coefficient matrix

在求解荷載矩陣Q時，令

(15)

根據理論公式(15)，可以求得荷載矩陣Q的各項參數，如表3所示。將以上數據代入式(9)和式(10)，可以求得翼板和腹板交界位置以及翼板中心位置的剪力滯系數，計算結果如表4所示。

表3 荷載矩陣計算Table 3 Calculation of the load matrix

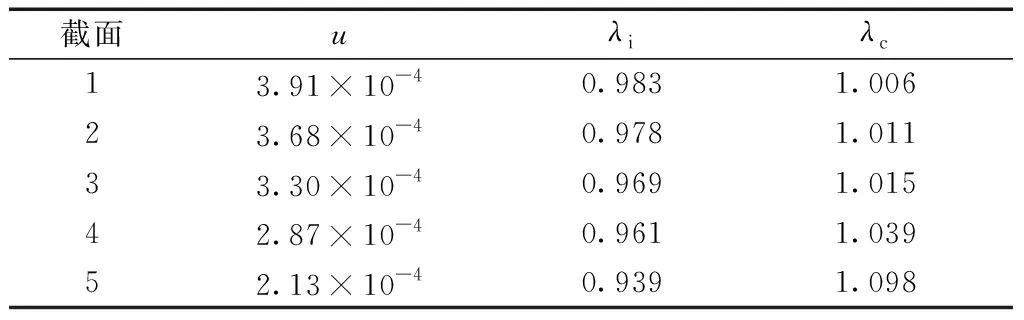
表4 翼緣板剪力滯計算Table 4 Calculation of the shear lag effect of the flange plate

為了更好地觀察變截面箱型懸臂梁的剪力滯變化規律，現將上表計算的剪力滯系數繪于圖5中。

由圖5可知：變截面箱型連續梁在施工階段的自重荷載作用下，翼板出現負剪力滯效應。剪力滯效應在固定端最小，隨著離固定端距離的增大，剪力滯效應也在逐漸增大。在頂板和腹板交界處的剪力滯系數最小為0.939，在翼板中心處剪力滯系數最大為1.098。

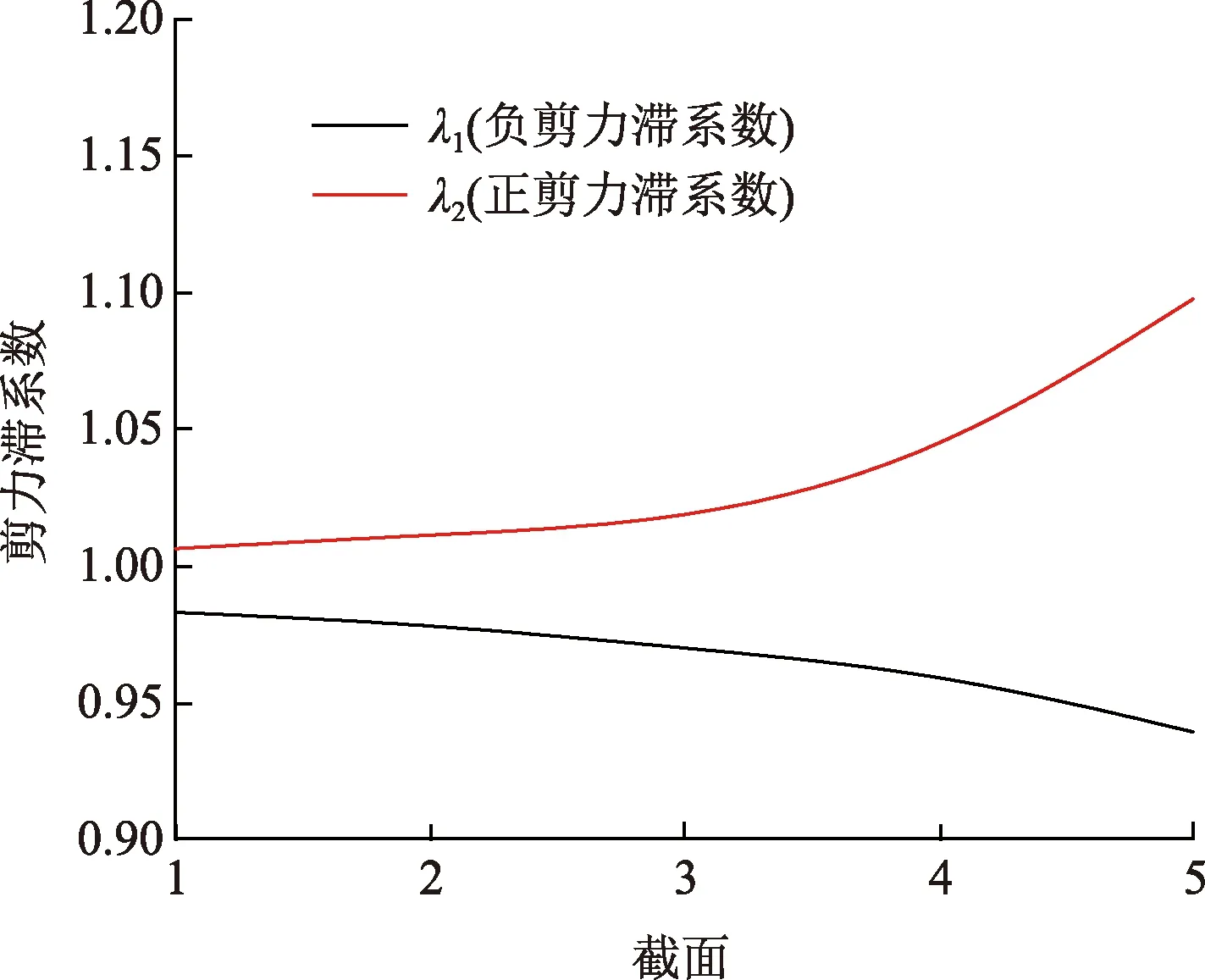
圖5 翼緣板剪力滯變化規律Fig.5 Shear lag effect of the flange plate

負剪力滯效應會造成梁體翼板的損壞，甚至造成橋梁倒塌的破壞。為了進一步深入研究變截面箱型梁的剪力滯效應，利用有限元模擬和現場試驗的手段，對采用掛籃法施工的變截面箱梁的剪力滯效應做進一步的研究。

3 現場試驗

3.1 測點布置

考慮到連續梁的實際情況，在主梁全跨度范圍內對稱設置7個測試截面，分別是邊跨合龍段、零號塊、中跨零號塊和合龍段，具體截面選擇如圖6所示。

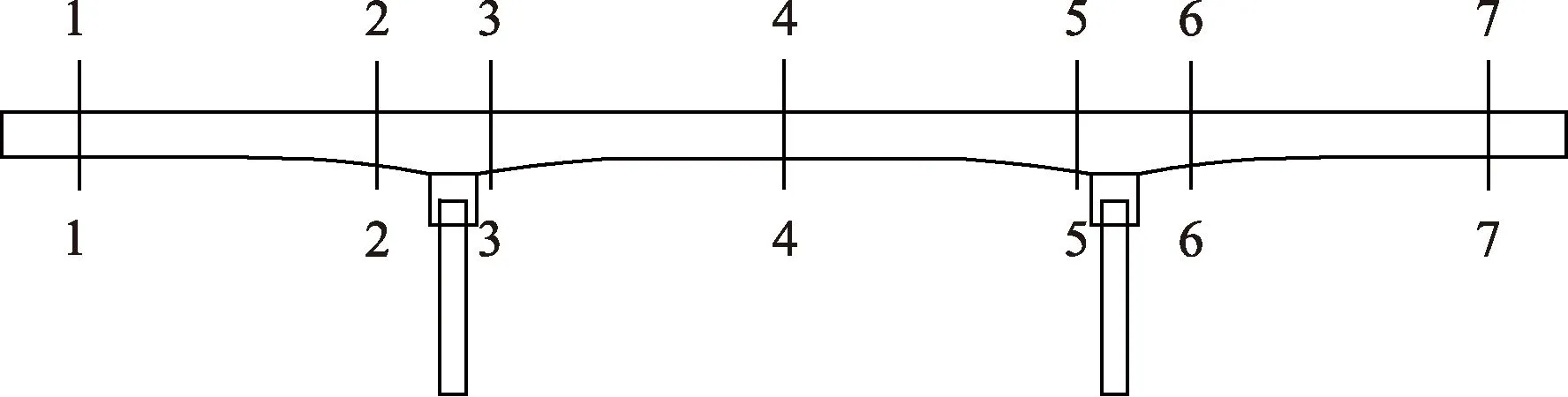
圖6 測試截面選擇Fig.6 Selection of the test cross-section

對橋梁結構的實際受力狀態進行跟蹤監測，不僅可以評價施工的質量，還可以準確地掌握結構的真實應力狀態。測試截面一共埋置4個傳感器，測點布置如圖7所示。

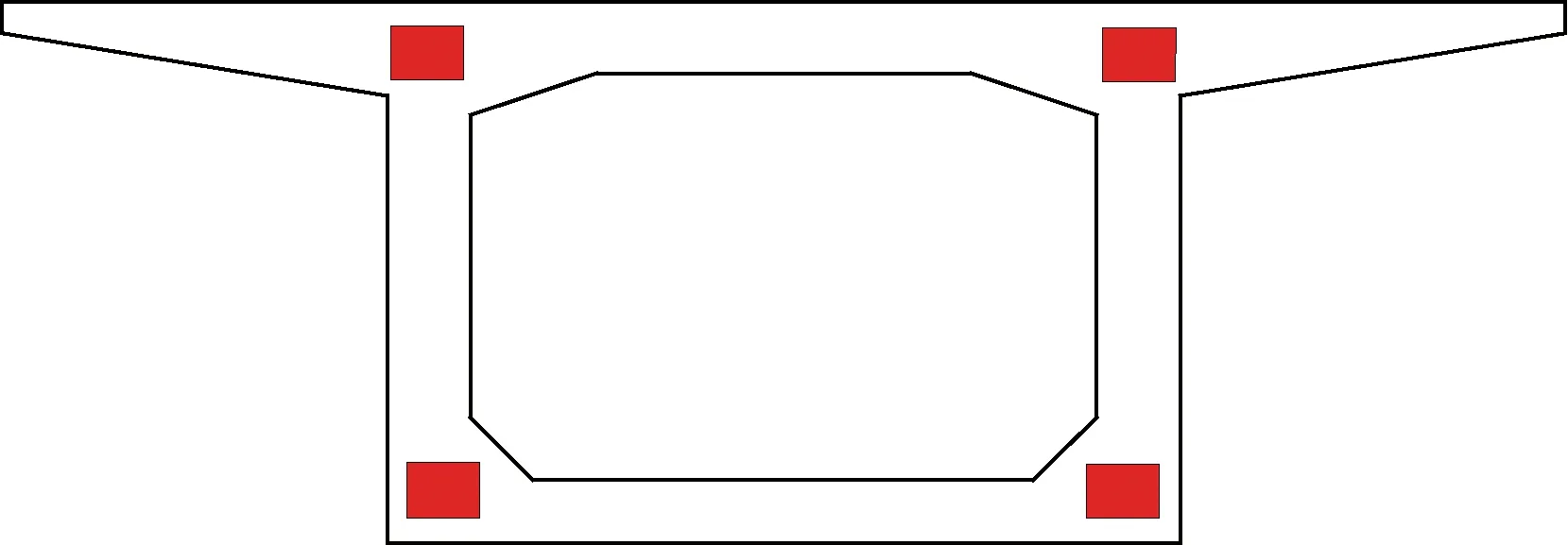
圖7 測點布置Fig.7 Layout of measuring points

3.2 傳感器布置和數據采集

測試儀器采用振弦式智能溫控應力傳感器，后端設備采用SS-II頻率接收儀和ZHX-1振弦檢測儀，根據選定的截面和測點位置，對每一個施工階段的應力(應變)數據進行采集，如圖8所示。

圖8 現場傳感器布置和數據采集Fig.8 Arrangement of the sensors and the data collection

4 剪力滯效應結果分析

4.1 建立有限元模型

在數值模擬時，采用MIDAS/civil建立梁單元模型，可以有效地計算得到按初等梁理論計算所得的梁截面彎曲應力，全橋總共61個節點，60個梁單元；利用MIDAS/FEA建立實體單元模型，可以有效地得到考慮剪滯效應的彎曲應力，全橋總共8 779個節點，共26 774個實體單元。將最后計算的結果，同現場實驗值進行對比分析，有限元模型如圖9所示。

圖9 變截面箱梁有限元模型Fig.9 Finite element model of variable section box girder

利用有限元模擬，重點對0號塊梁端截面和1號塊梁端截面的剪力滯進行對比分析，其次是對成橋階段的全橋沿縱向的剪力滯規律進行分析。

4.2 有限元計算結果分析

施工荷載考慮掛籃自重、現澆混凝土自重和張拉預應力荷載，掛籃懸臂施工的最大懸臂狀態是在澆筑9號塊時，此時也是最不利荷載工況，此時0號塊的縱向正應力如圖10所示。

圖10 最大懸臂狀態時0號塊彎曲應力Fig.10 Bending stress of block 0 at maximum cantilever state

利用MIDAS/FEA建立實體單元有限元模型可以有效模擬實際施工中的梁體，從而求得實際的縱向正應力；利用MIDAS/civil建立梁單元有限元模型，求得在初等梁理論假設下的縱向正應力。分別對0號塊梁端截面和1號塊梁端截面的頂板和底板剪力滯在整個施工過程中的變化規律進行了計算總結，結果如圖11和圖12所示。

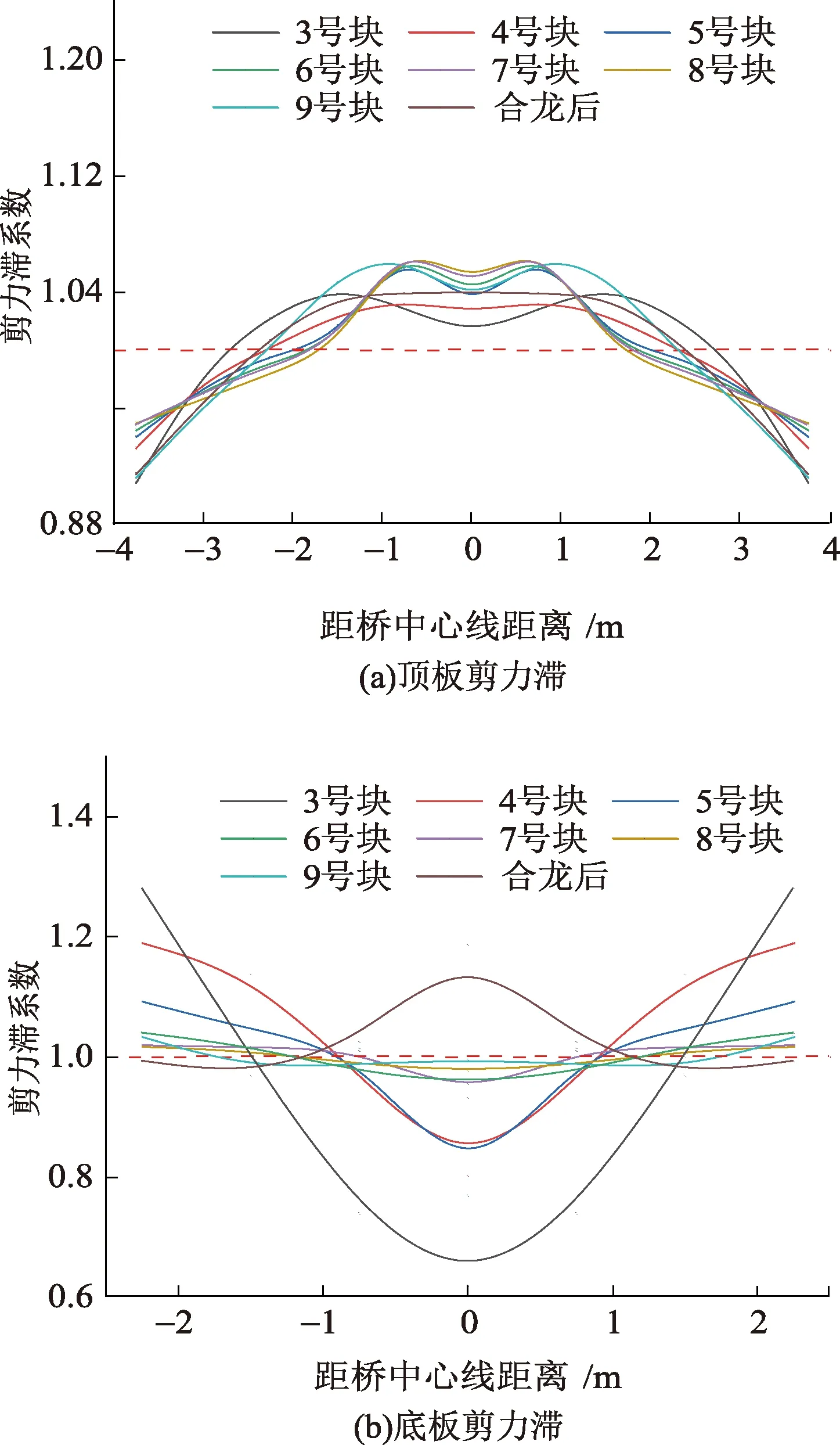
圖11 0號梁端截面剪力滯橫向變化規律Fig.11 Shear lag effect of the cross section of block-0

圖12 1號梁端截面剪力滯橫向變化規律Fig.12 Shear lag effect of the cross section of block-1

由圖11可以看出，在梁體自重荷載作用下的整個施工階段，0號梁端截面頂板出現負剪力滯，在9號塊鋼束張拉后剪力滯效應最明顯，最大剪力滯系數為1.06，隨著施工的進行，剪力滯效應在不斷減小；0號梁端截面底板出現正剪力滯，且在澆筑3號塊后剪力滯效應最明顯，剪力滯系數最大為1.28，隨著施工的進行，剪力滯效應在不斷減小，且在合龍后，剪力滯效由正剪力滯變成負剪力滯，此時最大剪力滯系數為1.18。

由圖12可以看出，在施工荷載作用下的整個施工階段，1號梁端截面頂板出現負剪力滯，隨著施工的進行，剪力滯效應在不斷減小；1號梁端截面底板出現正剪力滯，且在澆筑3號塊后剪力滯效應最明顯，剪力滯系數最大為1.15，隨著施工的進行，剪力滯在不斷減小，且在合龍后，剪力滯效由正剪力滯變成負剪力滯，此時最大剪力滯系數為1.13。

4.3 有限元結果和實測值對比分析

根據振弦式智能溫控應力傳感器測得應變，進一步計算得到實橋應力，再根據剪力滯的定義，求得實際施工中的剪力滯變化規律，再與有限元值進行對比分析，結果如圖13和圖14所示。

圖13 0號梁端截面剪力滯效應Fig.13 Shear lag effect of beam end section of No. 0 beam

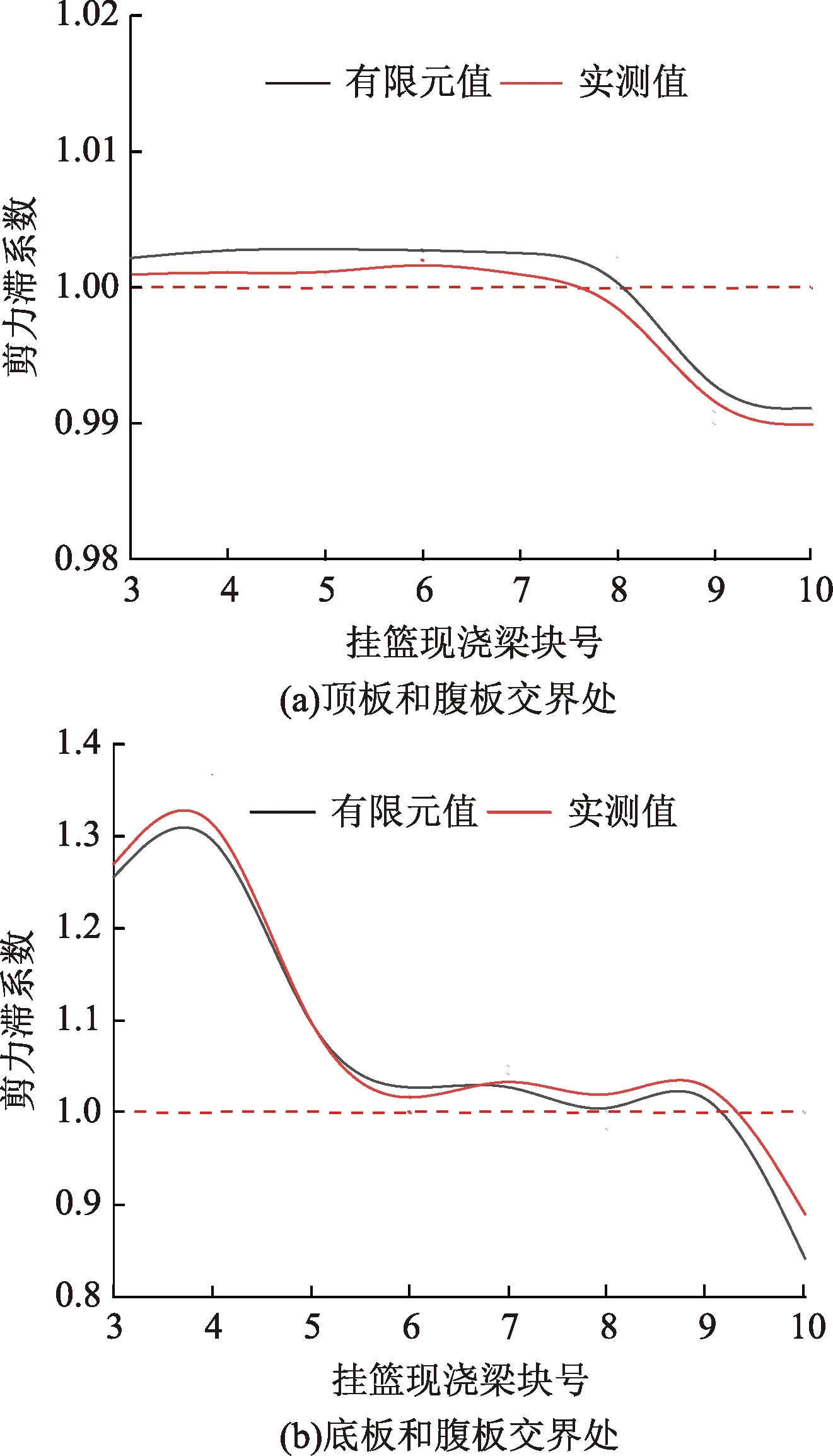
圖14 1號梁端截面剪力滯效應Fig.14 Shear lag effect of beam end section of No. 1 beam

由圖13可以看出，隨著施工的進行，在0號塊梁端截面的頂板與腹板交界處出現負剪力滯，剪力滯效應在不斷減小；在0號塊梁端截面的底板與腹板交界處出現正剪力滯，剪力滯系數在逐漸減小。因此在施工過程中，需重點觀察頂板應力，對頂板應力變化實時監控，避免出現應力超限而破壞。

由圖14可以看出，隨著施工的進行，在1號塊梁端截面的頂板與腹板交界處出現正剪力滯，剪力滯效應在不斷減小；在0號塊梁端截面的底板與腹板交界處出現正剪力滯，剪力滯效應在逐漸減小。其中底板和腹板交界處剪力滯系數最大達到1.34，在施工中應可采取合理配置鋼筋和增加角隅等措施來改善此處的受力。

5 結論

以某新建(48+80+48) m變截面箱型預應力混凝土連續梁橋為工程背景，進行其施工階段剪力滯分析，得到如下結論。

(1) 變截面箱型連續梁在施工階段的自重荷載作用下，翼板出現負剪力滯效應。剪力滯效應在固定端最小，隨著離固定端距離的增大，剪力滯效應也越明顯。

(2) 在整個施工階段，0號塊和1號塊的頂板均出現負剪力滯效應，隨著施工的進行，剪力滯效應在逐漸減小；底板均出現正剪力滯，隨著施工的進行，剪力滯效應在逐漸減小。

(3) 在梁體合龍后，0號塊和1號塊的底板剪力滯效由正剪力滯變成負剪力滯。

(4) 隨著施工的進行，0號塊梁端頂板和腹板交接處的剪力滯系數在逐漸增大，在底板和腹板交接處剪力滯系數在逐漸減小，1號塊梁端截面頂板和腹板交接處、底板和腹板交接處剪力滯系數逐漸減小。