含多狀態嚙合與時變參量的直齒錐齒輪動態特性

茍向鋒， 李谷雨， 朱凌云

(天津工業大學 機械工程學院，天津 300387)

齒輪傳動的振動和噪聲嚴重影響其精度、承載能力和穩定性。設計中為防止輪齒卡死而預留的齒側間隙，決定了其傳動過程中會出現齒面嚙合、輪齒脫嚙和齒背接觸。齒輪副的重合度一般大于1.0，導致齒輪的嚙合齒數是時變的。二者綜合作用的結果使齒輪嚙合時存在單/雙齒齒面嚙合、輪齒脫嚙和單/雙齒齒背接觸等多種狀態，造成輪齒沖擊，影響傳動平穩性。Gou等考慮齒輪副的多狀態嚙合特性，分別建立了直齒輪副[1]和面齒輪傳動系統[2]的非線性動力學模型，為揭示齒輪傳動系統的動態特性奠定了方法基礎。

錐齒輪齒廓結構復雜，其動力學研究成果較少。Karray等[3]建立了一種單級錐齒輪動力學模型，研究了齒輪局部損傷對動力學特性的影響。Kiyono等[4]建立了一種兩自由度的錐齒輪副動力學模型，分析了錐齒輪與直齒輪、斜齒輪的動力學特性差異。Wang等[5]基于有限元法，建立了包含軸和軸承的錐齒輪傳動系統動力學模型。Cheng等[6-7]基于TCA方法得出了錐齒輪接觸點軌跡，建立了一種改進的錐齒輪傳動系統動力學模型。Yassine等[8]分析了故障錐齒輪系統的動力特性，并與無故障錐齒輪系統的動力特性進行比較。方宗德等[9]建立了包含時變剛度和誤差激勵的多自由度直齒錐齒輪傳動系統動力學模型。王三民等[10]建立了包含多種時變參數的八自由度弧齒錐齒輪傳動系統動力學模型。王立華[11]建立了含多種時變參數的12自由度弧齒錐齒輪傳動系統動力學模型，研究了其動力學特性。蔣函成等[12]建立了考慮軸系和機匣柔性性的齒輪-轉子-機匣耦合系統動力學模型，推導了各類齒輪副的嚙合關系。這些研究主要關注系統參數計算、動力學建模及非線性動力學特性研究，未考慮重合度對系統嚙合特性的影響。

基于錐齒輪嚙合原理，利用微元法計算錐齒輪傳動系統的時變嚙合剛度和載荷分配率；建立含時變嚙合剛度、載荷分配率、綜合傳遞誤差和軸承支承的錐齒輪傳動系統多狀態嚙合動力學模型。通過定義不同的Poincaré截面，研究嚙合頻率和綜合傳遞誤差對系統嚙合狀態和動態特性的影響，為系統參數設計和優化提供理論依據。

1 時變參數的計算

錐齒輪傳動系統動力學模型的準確性受時變參數計算模型準確性的影響。由于錐齒輪齒廓較為復雜，現有研究計算其時變參數時都進行了簡化。本文基于錐齒輪嚙合原理利用微元法建立時變參數計算模型。

1.1 直齒錐齒輪模型及受力分析

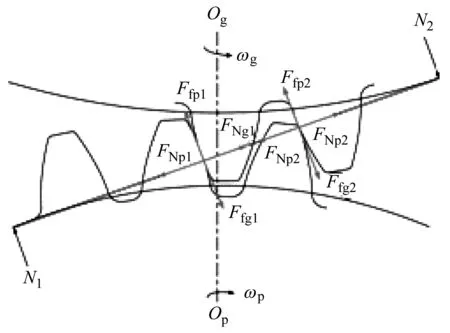
考慮齒側間隙和軸承支承的直齒錐齒輪傳動系統簡化物理模型如圖1所示。p和g分別代表主動輪和從動輪，其當量齒輪的基圓半徑為Rbj、扭轉振動位移為θj、慣性矩為Ij，扭矩為Tj，k(τ)為時變嚙合剛度，Cm為嚙合阻尼系數。en(τ)為沿嚙合線方向的綜合傳遞誤差。2Dn為齒側間隙，kjl、Cjl和Djl分別為沿l方向的軸承支承剛度、軸承支承阻尼系數和軸承間隙。其中，j=p,g和l=X,Y,Z。

圖1 直齒錐齒輪傳動系統簡化物理模型

表1為某汽車差速器中直齒錐齒輪傳動部分的系統參數。其重合度為1.353，結合齒側間隙的影響，該直齒錐齒輪傳動中存在單/雙齒齒面嚙合、輪齒脫嚙、單/雙齒齒背接觸等五種嚙合狀態。

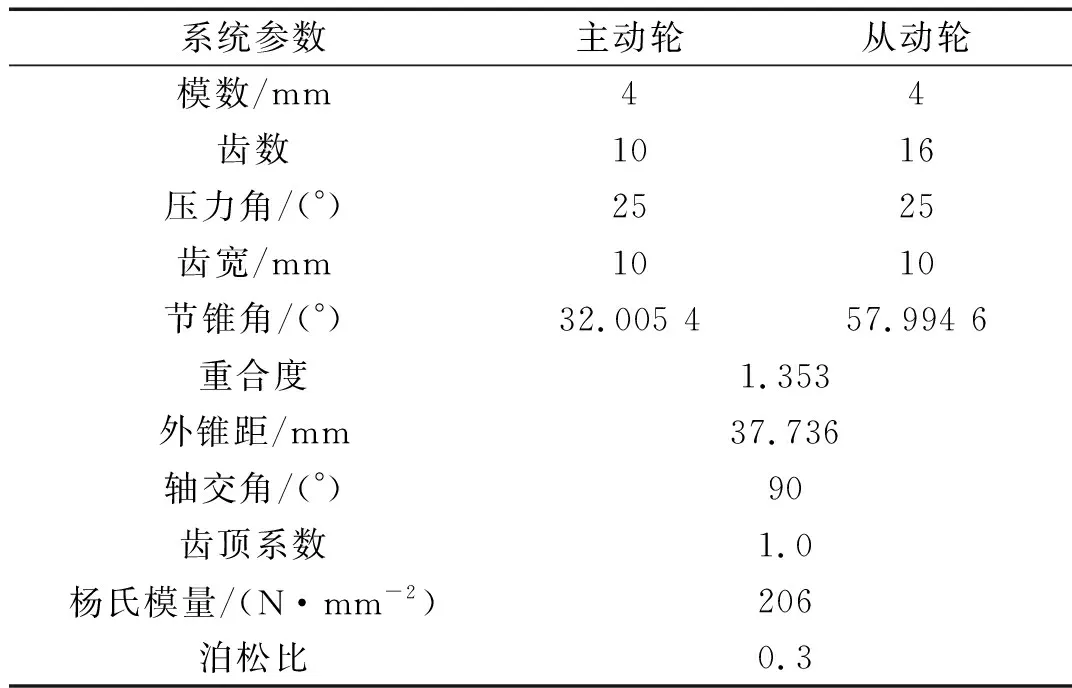
表1 汽車差速器中直齒錐齒輪傳動系統參數

設δp和δg分別為主、從動輪的節錐角，Xj、Yj、Zj(j=p,g)分別為兩齒輪沿X、Y、Z方向的振動位移，αn為兩齒輪的壓力角，Fn和Ff為嚙合點上的正壓力和摩擦力，Fnl和Ffl(l=X,Y,Z)分別為其沿l方向的分量，則齒輪副沿嚙合點法向的相對位移如式(1)所示。

(1)

式中：a1=cosδpsinαn、a2=cosδgsinαn、a3=sinδpsinαn、a4=sinδgsinαn、a5=cosδpsinαn、a6=cosδgsinαn；rp和rg分別為嚙合點到兩輪齒旋轉中心的距離。

錐齒輪嚙合點處的正壓力Fn和摩擦力Fnl及其分量可由式(2)獲得[13]。

(2)

1.2 時變嚙合剛度

齒輪嚙合剛度是影響齒輪承載能力及動力學特性的重要參數。錐齒輪嚙合剛度主要采用Tredgold近似，即利用微元法將錐齒輪齒廓沿齒寬方向簡化為無數個微元近似求解。在Lafi等[14]研究基礎上，引入了輪齒基體剛度，建立直齒錐齒輪嚙合剛度計算模型。

微元齒輪的嚙合剛度ko包括赫茲接觸剛度kho，輪齒基體剛度kfo，彎曲剛度kbjio，軸向壓縮剛度kajio，剪切剛度ksjio(i=1,2;j=p,g)，分別可由式(3)～(7)得到。

(3)

(4)

(5)

(6)

(7)

式中：w=L*(uf/Sf)2+P*(1+Q*tan2α)+M*(uf/Sf);q=cosσjio[l1/Rbjo+cosθjo-cosα+(θjo-α)sinα]-h1sinσjio/Rbjo;E和ν分別為楊氏模量和泊松比;σjio為沿齒寬方向第o個微元齒輪嚙合線與齒中心線的夾角;θjo=0.5π/zjo+invα為沿齒寬方向的第o個微元齒輪的齒角半值;Nj為沿齒寬方向微元齒輪的數量;直齒錐齒輪嚙合剛度可由式(8)獲得。

(8)

根據重合度可將齒廓嚙合區域分為單齒嚙合區BC、雙齒嚙合區AB和CD。則齒輪的單/雙齒嚙合時間分別為tAB=tCD=(εm-1)T0，tBC=(2-εm)T0，其中，T0=tAC=2π/(ωPzP)為單雙齒嚙合交替時間[1]。假定齒背接觸時的嚙合剛度與齒面嚙合時相同，表1所示直齒錐齒輪副的嚙合剛度如圖2所示。

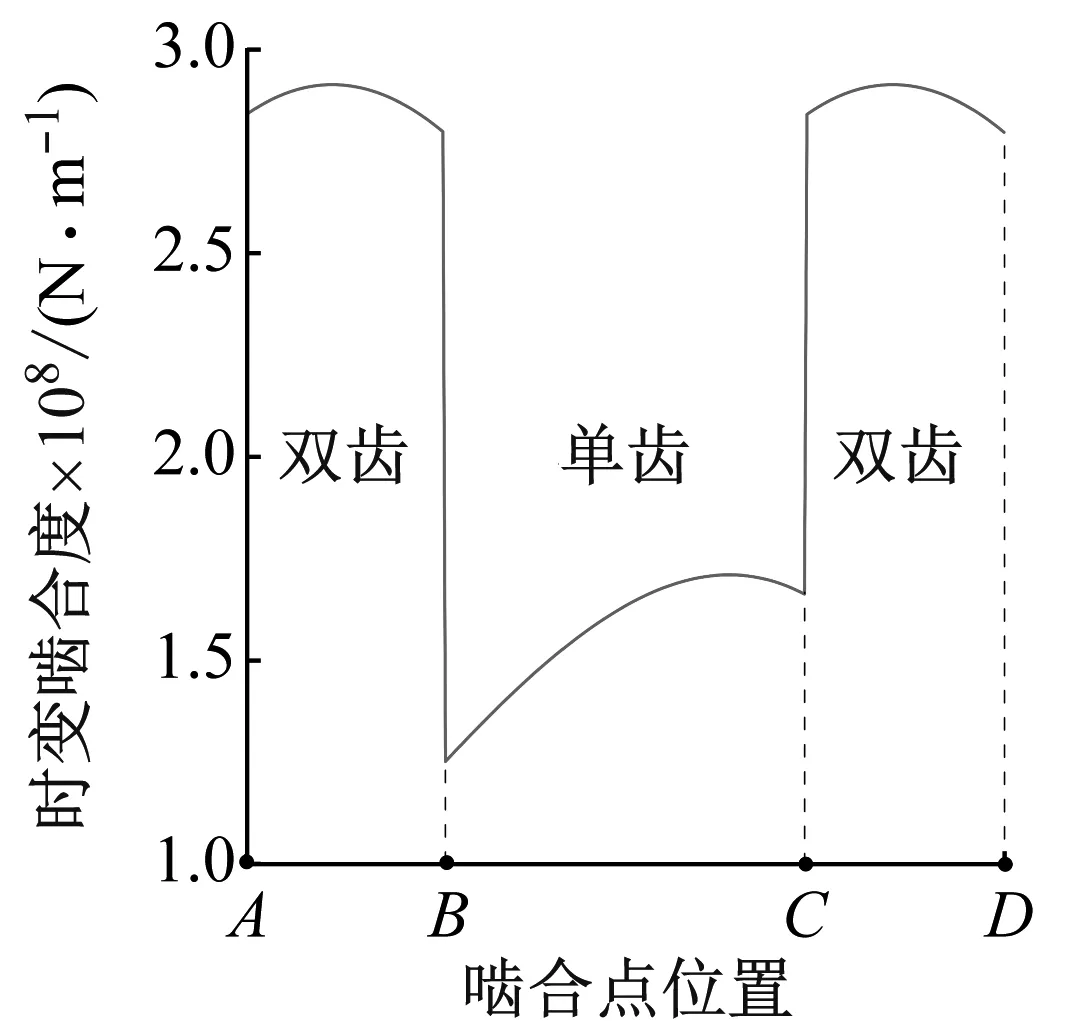
圖2 直齒錐齒輪時變嚙合剛度

1.3 載荷分配率

直齒錐齒輪副的重合度一般大于1.0，齒輪在嚙合時會出現多對齒同時嚙合，導致載荷在嚙合輪齒間的分配，則載荷分配率不可忽視。目前尚無其計算方法的報道。根據文獻[15-16]中斜齒輪載荷分配率的求解方法，將錐齒輪輪齒沿齒寬方向分為無數個微元齒輪，結合最小勢能法建立直齒錐齒輪載荷分配率模型。

齒輪的總勢能U由微元齒輪的勢能Uo疊加得到，如式(9)所示。

(9)

微元齒輪的彎曲勢能Ubjio、壓縮勢能Uajio和剪切勢能Usjio(i=1,2;j=p,g)可分別由式(10)～(12)得到。

(10)

(11)

(12)

微元齒輪的勢能Uo可由式(13)得到。

(13)

根據彈性勢能原理和拉格朗日方法，可得直齒錐齒輪載荷分配率如式(14)所示。

(14)

式中，νs表示輪齒的逆單位勢能。包含多狀態嚙合特性的直齒錐齒輪載荷分配率模型如式(15)所示。

(15)

式中，Ld(τ)和Lk(τ)分別為齒面嚙合狀態和齒背接觸狀態下的載荷分配率。計算表1所示錐齒輪副的載荷分配率如圖3所示，圖3中實線代表第i嚙合齒對的載荷分配率，AB段和CD段虛線分別代表第i-1和i+1嚙合齒對的載荷分配率。

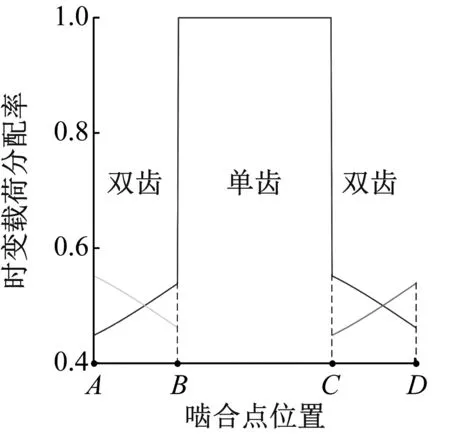
圖3 直齒錐齒輪載荷分配率

2 考慮多狀態嚙合的直齒錐齒輪傳動系統彎-扭-軸動力學建模

直齒錐齒輪副嚙合可視為嚙合點法面(背錐面)上兩個當量齒輪嚙合。其齒面嚙合狀態和齒背接觸狀態及受力如圖4所示。齒面嚙合時，主動輪沿嚙合線N1N2推動從動輪；齒背接觸時，從動輪齒背齒廓沿嚙合線M1M2推動主動輪。FNpi、FNgi分別為沿嚙合線N1N2、M1M2的正壓力分力，Ffpi、Ffgi分別為垂直于嚙合線N1N2、M1M2的摩擦力分力。由錐齒輪嚙合原理可知：假定N1→N2或M1→M2為正壓力的正方向，則FNg1+FNg2>0時為齒面嚙合，FNg1+FNg2<0時為齒背接觸；FNg1+FNg2=0時為輪齒脫嚙。則，齒面嚙合時Xn>Dn，齒背接觸時Xn<-Dn，輪齒脫嚙時-Dn≤Xn≤Dn。基于集中質量法和牛頓第二定律，可得多狀態嚙合時直齒錐齒輪傳動系統的彎-扭-軸動力學模型。

(16)

式中，±和?中上方的符號表示齒面嚙合，下方的符號表示齒背接觸。FNpi=FNgi=Lci(τ)Fn、Ffpi=Ffgj=λci(τ)Lci(τ)μcFn(c=d,k)，d代表齒面嚙合，k代表齒背接觸，mjl(j=p,g；l=X,Y,Z)為沿l方向的集中質量，λci(c=d,k;i=1,2)為第i個嚙合齒對的摩擦力方向系數，μc(c=d,k;i=1,2)為輪齒表面的摩擦力系數。

(a) 齒面嚙合

由式(2)可求得直齒錐齒輪正壓力和摩擦力沿坐標軸方向的分力，如式(17)～(18)所示。

(17)

(18)

式中：λci(τ)=sign[vci(τ)]；vci(τ)(c=d,k;i=1,2)為輪齒的相對滑動速度，如式(19)所示；Scji(τ)(c=d,k;i=1,2;j=p,g)為兩齒輪的摩擦力臂，如式(20)～(22)所示；sign為符號函數。

式中：Scj2(τ)=Scj1(τ+T0)(c=d,k)；rbj(j=p,g)為兩齒輪齒寬中部的基圓半徑；Rbj=rbj/cosδj(j=p,g)，Rag為從動輪齒頂圓半徑；兩齒輪的壓力角αcji(τ)和嚙合點到兩輪齒旋轉中心的距離Rcji(τ)Scji(τ)(c=d,k;i=1,2;j=p,g)可由式(23)～(25)得到。

αcj1(τ)=arccos[Rbj/Rcj1(τ)]

(23)

(24)

αcj2(τ)=αcj1(τ+T0),Rcj2(τ)=Rcj1(τ+T0)

(25)

整理式(16)～(25)，可得直齒錐齒輪傳動系統彎-扭-軸無量綱歸一化動力學方程。

(26)

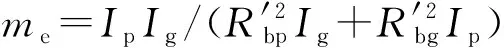
軸承的無量綱化間隙函數如式(27)所示。

(27)

式中，q代表xp、yp、zp、xg、yg、zg。rl(t,xn)(l=x,y,z)為沿l方向的嚙合狀態函數，如式(28)～(29)所示；h(t,xn)為沿正壓力方向的嚙合狀態函數，如式(30)所示。

rx(t,xn)=ry(t,xn)=

(28)

rz(t,xn)=

(29)

h(t,xn)=

(30)

3 參數對系統動態特性的影響

系統中存在齒面嚙合、輪齒脫嚙和齒背接觸等嚙合狀態。為研究不同參數下各嚙合狀態對系統動力學特性的影響，定義三個不同的Poincaré截面：

系統的多狀態嚙合行為可由符號N-P-Q表征，其中，N表示系統運動周期數，P表示輪齒脫嚙次數，Q表示齒背接觸次數，若P或Q為零，表明系統無輪齒脫嚙或齒背接觸。

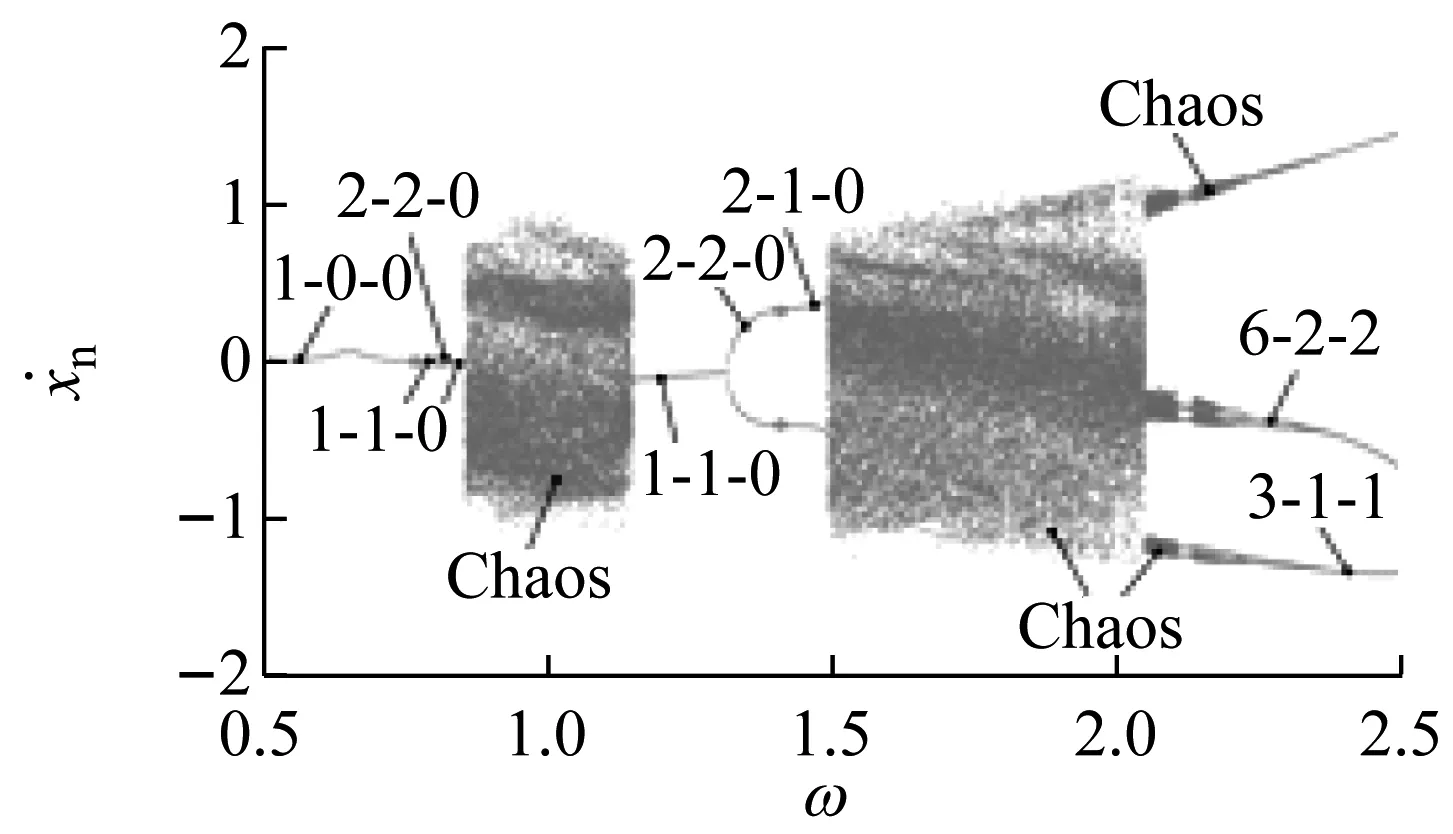
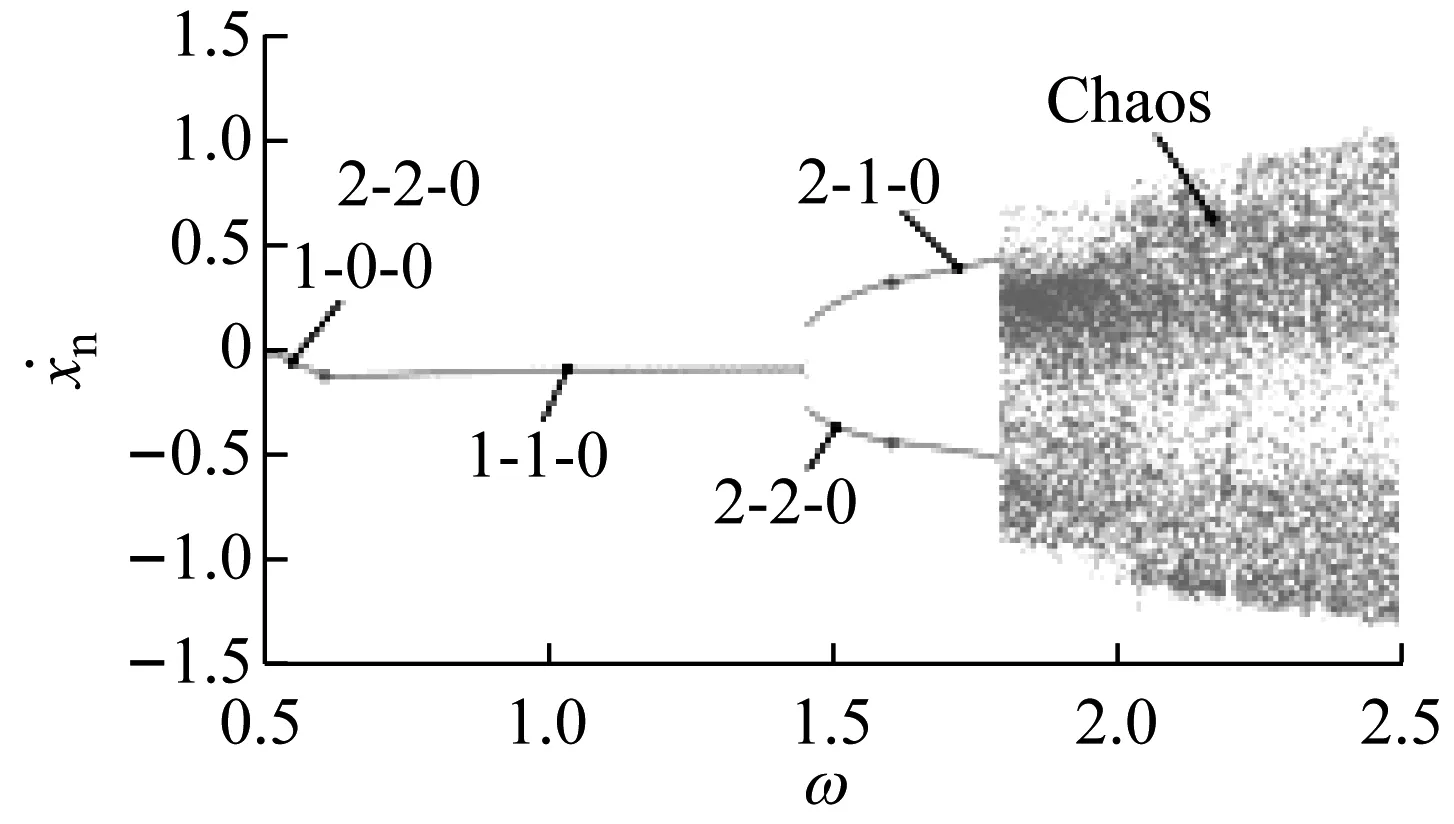
3.1 嚙合頻率ω的影響

(a) Γn

當ω較小時，系統為1-0-0運動，完全齒面嚙合狀態，無輪齒脫嚙和齒背接觸。當ω增大至ω=0.73(A1)時，系統相軌跡與x=D相切，此時相圖和時間歷程圖為圖6(a)和6(b)所示。當ω增大至A1點右側時，系統處于1-1-0運動，系統依舊為周期1運動，但出現了輪齒脫嚙。當ω增大至A2點時，1-1-0運動經倍化分岔進入2-2-0運動，系統相軌跡兩次穿越齒側間隙邊界，此時對應的TLE值接近0。

當ω增加到A3點時，2-2-0運動經逆倍化分岔退化為1-1-0運動，其對應的TLE值近似為0，之后經鞍結分岔進入混沌運動，此時系統中同時存在齒面嚙合、輪齒脫嚙和齒背接觸三種運行狀態，其Poincaré映射圖和時間歷程圖如圖6(c)和6(d)所示。當ω增大至A4點時，系統經鞍結分岔由混沌運動退化為1-1-0運動，系統中齒背接觸消失。當ω增大至A5點時，1-1-0運動倍化為2-2-0運動，此時系統中存在齒面嚙合和輪齒脫嚙兩種運動狀態。當ω增大至A6點時，系統相軌跡與x=D相切，2-2-0運動經擦切分岔轉遷為2-1-0運動，此時相圖和時間歷程圖為圖6(e)和6(f)所示。

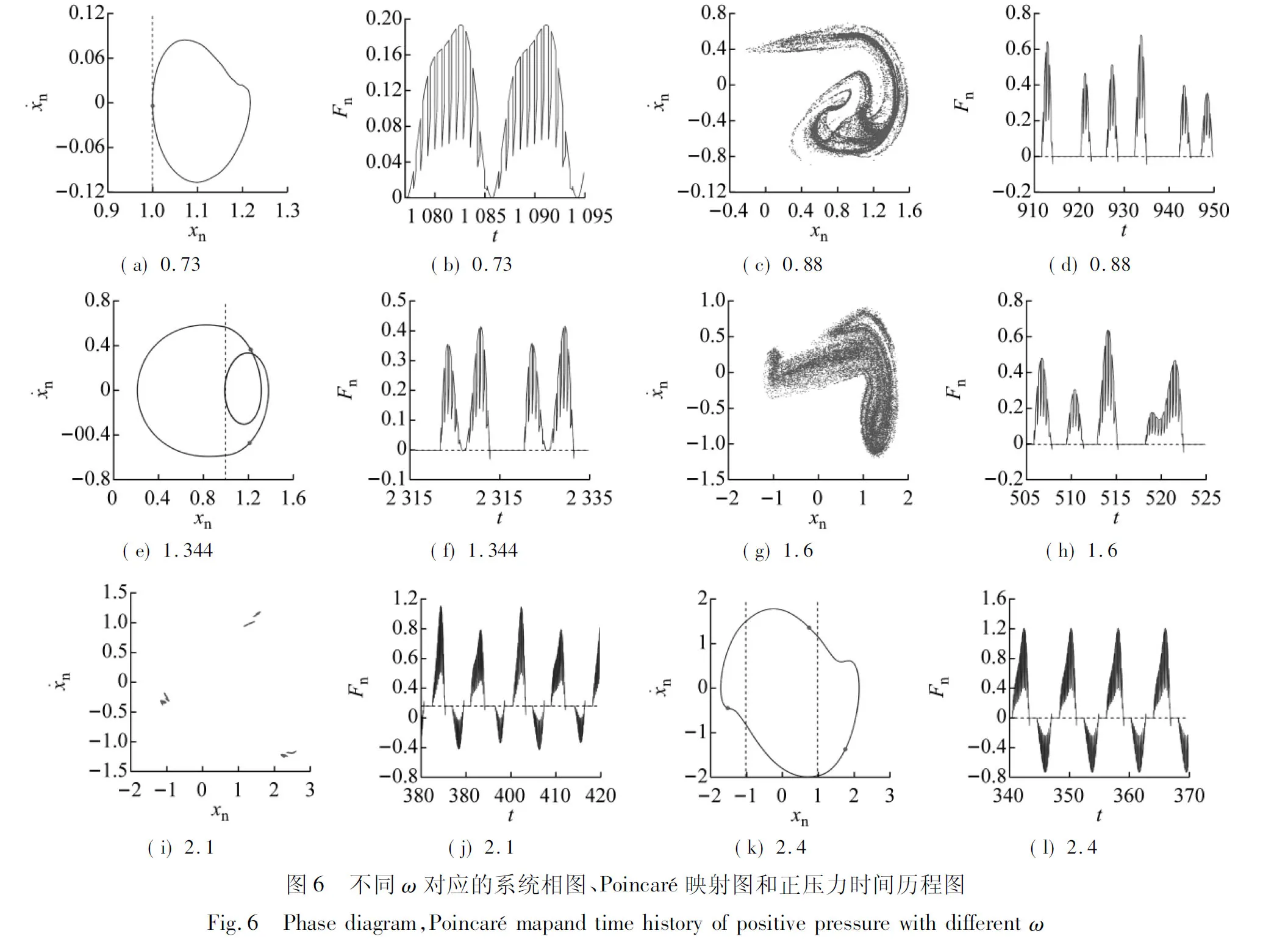
該2-1-0運動在A7點經鞍結分岔進入混沌運動，其對應的TLE>0，此時Poincaré映射圖和時間歷程如圖6(g)和6(h)所示，混沌區域系統出現了齒面嚙合、輪齒脫嚙和齒背接觸三種運行狀態。隨著ω增大，A8～A9點系統出現了新的混沌運動，其拓撲結構與之前不同，此時Poincaré映射圖和時間歷程圖如圖6(i)和6(j)所示。

當ω>2.2(A9點右側)時，系統經逆倍化分岔序列由混沌運動退化為6-2-2運動。當嚙合頻率增加到A10點時，6-2-2運動逆倍化為3-1-1運動，其對應的TLE值發生了突變，此時Poincaré映射圖和時間歷程圖分別如圖6(k)和6(l)所示。

可見，當嚙合頻率較小時，系統處于穩定的齒面嚙合狀態。隨著嚙合頻率的增加，系統逐漸出現輪齒脫嚙，其運動類型也由穩定的周期1運動轉遷為復雜的多周期運動，在1倍頻和1.5倍頻附近系統表現為混沌運動，且在混沌運動區域系統出現了齒背接觸狀態，在2.2倍頻以后系統重新出現多周期運動，但齒背接觸狀態依舊存在。隨著嚙合頻率的增加，系統多狀態嚙合行為和運動特性變得復雜，選擇合理嚙合頻率可獲得期望的運動特性。

3.2 綜合傳遞誤差ε的影響

取無量綱參數ω=0.73、F=0.1、ζ=0.05，其余參數取值與3.1相同，可得綜合傳遞誤差ε增大的三種Poincaré截面分岔圖和TLE圖如圖7。

(a) Γn

當ε較小時(B1點左側)，系統處于穩定的1-0-0運動，只存在齒面嚙合。ε增大至B1點時，系統相軌跡與xn=D相切，1-0-0運動經擦切分岔轉遷為1-1-0運動，系統中出現了輪齒脫嚙，由于振動幅值較小，所以系統單雙齒交替嚙合影響較為明顯，系統相軌跡出現波動，此時相圖和時間歷程圖為圖8(a)和8(b)所示。ε增大到B2點，系統經倍化分岔由1-1-0運動轉遷為2-2-0，系統中存在齒面嚙合和輪齒脫嚙兩種運行狀態。

隨著ε增大到B3點時，系統經擦切分岔由2-2-0運動退化為2-1-0運動，系統相軌跡穿過齒側間隙的半值由之前的兩次減少為一次，此時相圖和時間歷程圖為圖8(c)和8(d)所示。當ε增大到B4點時，系統經鞍結分岔由2-1-0運動轉遷為混沌運動，混沌區域內系統出現齒面嚙合、輪齒脫嚙和齒背接觸三種運行狀態，此時相圖和時間歷程圖為圖8(e)和8(f)所示。

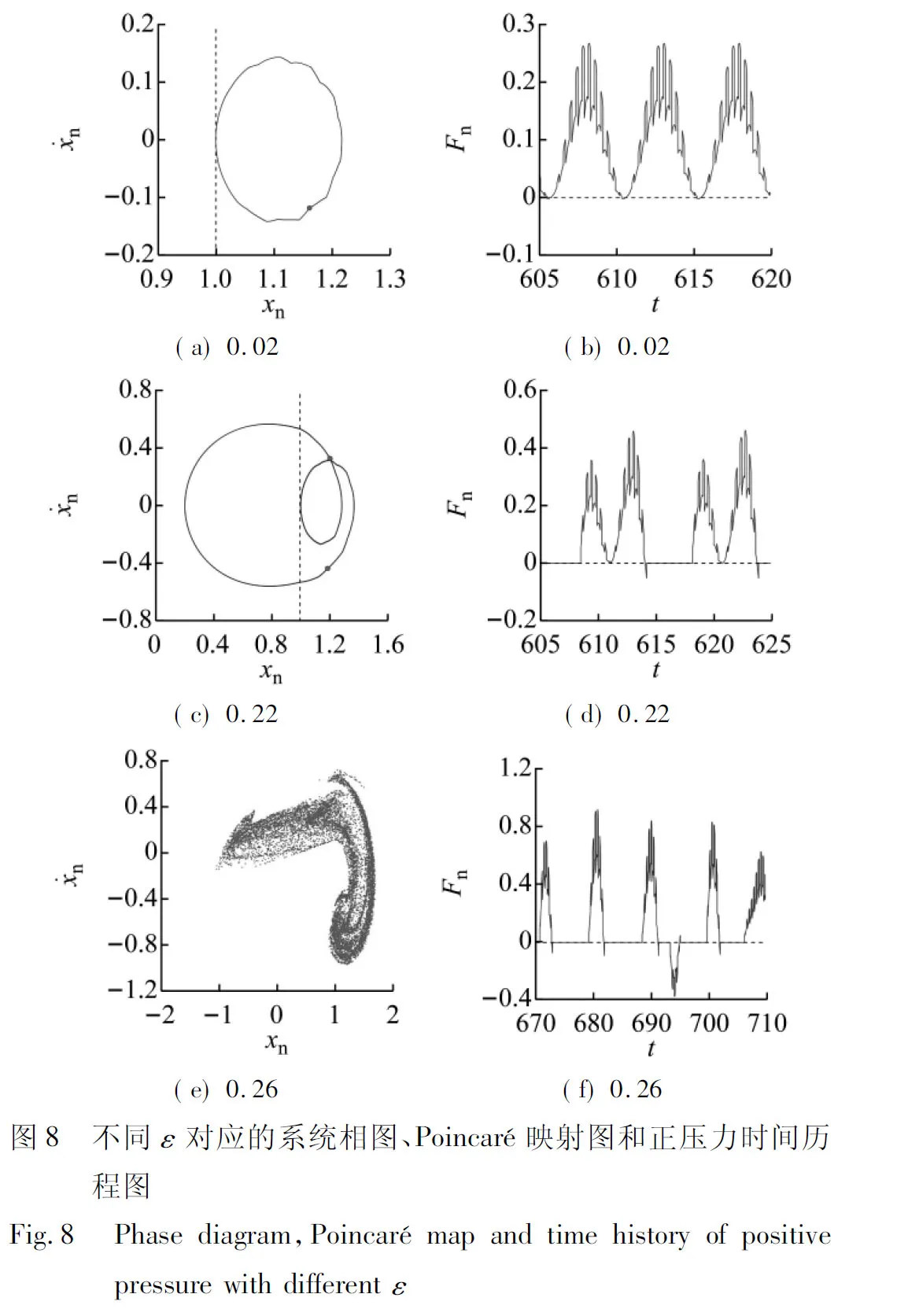
可見，隨著綜合傳動誤差波動幅值的增大，系統中逐漸出現了輪齒脫嚙和齒背接觸狀態，其多狀態嚙合行為和運動特性變得復雜，穩定性隨之惡化。因此，應提高直齒錐齒輪傳動系統的制造精度、減小綜合傳遞誤差，以提高其運動平穩性。

4 結 論

考慮多狀態嚙合、載荷分配率、時變嚙合剛度和齒側間隙，建立了直齒錐齒輪傳動系統彎-扭-軸動力學模型。采用微元法計算了載荷分配比和時變嚙合剛度。基于Poincaré映射理論和分岔理論，研究了嚙合頻率和綜合傳動誤差對系統動態特性的影響。結論如下：

(1) 結合本文建立的直齒錐齒輪傳動系統彎-扭-軸動力學模型和三種Poincaré截面，可以更加準確地揭示系統的動力學特性。

(2) 根據直齒錐齒輪傳動系統的嚙合原理，采用微元法計算的載荷分配率和時變嚙合剛度相比傳統方法計算更加準確，更能反映系統參數的運行規律。

(3) 當嚙合頻率較小時，系統的非線性動力學特性和動態嚙合特性簡單且穩定，隨著嚙合頻率的增加，系統的動態嚙合特性變得非常復雜；隨著綜合傳動誤差波動幅值的增大，系統的動態特性變得越來越復雜，系統的傳動平穩性也隨之惡化。