基于空間坐標與振動特征融合的機床切削狀態分類方法

王 晶， 程曉斌， 高 艷， 王 勛， 楊 軍

(1. 中國科學院噪聲與振動重點實驗室(聲學研究所)， 北京 100190； 2. 中國科學院大學， 北京 100049)

在機械加工中，使用獨立的物理系統對機床切削參數進行監測可以直接感知物理信號的變化，反映機床實際的切削狀態，判斷其狀態與生產計劃是否一致，保證生產效率和生產質量[1]。在實際生產中，機床的硬件故障、數控系統故障和加工誤差等因素會導致機床沒有按照設定值正常運行[2]。具體表現為：(1) 硬件故障會導致機床切削參數未按指令值運行。例如主軸驅動故障會使主軸轉速偏離設定值；彈性聯軸器的開裂也會導致實際切深和切寬偏離設定值，使加工尺寸不穩定。(2) 數控系統故障會導致實際切削參數與指令值不一致。李夢群[3]指出數控系統故障會導致機床加工時執行數控代碼語句錯亂，未按生產計劃運行，或機床坐標軸未按數控面板顯示值移動，導致實際切深、切寬與設定不符。(3) 由零件裝夾等人工操作帶來的誤差會使實際切削不符合設定的運動軌跡，且這些誤差不能反饋至控制系統，導致實際切削量與計劃值不一致[4]。因此有必要使用獨立的物理系統監測實際切削參數，當計算出的切削參數受到物理信號異常影響與數控系統預定的參數值產生較大偏差時，可及時發現機床以非計劃值運行現象。

監測機床的切削狀態的常用手段是采集加工過程的振動信號[5]，并從中提取特征來描述有關機床狀態的信息。狀態監測的研究主要包括三個模塊，信號采集、特征提取和特征選擇[6-7]和工作狀態的分類[8]。為了全面描述復雜的切削過程和減小隨機干擾對信號帶來的影響，需要從振動信號中提取到豐富的特征構建高維特征池[9]。然而，高維特征池中存在非敏感特征，會干擾后續的分類準確率[10]。因此如選擇有效特征，去除高維特征池中的不相關信息對切削狀態分類尤為關鍵。

在工業中，流形學習被廣泛地用于特征選擇[11]。該算法通過非線性降維，能夠消除或減少數據之間的多重耦合和非敏感特征的干擾，有助于更好地理解切削狀態，建立更準確的分類模型。其中，t分布的隨機鄰域嵌入(t-distributed stochastic neighbor embedding, t-SNE)[12]是一種無監督算法，通過歐氏距離對數據點進行建模，捕捉局部結構的同時保持了全局結構，因此在工業狀態監測領域被廣泛地用作特征選擇方法[13]。

然而，無監督的流形學習算法在實際工業環境中的靈活度有限。其應用于切削狀態分類的局限性[14-16]主要體現在以下兩個方面：(1) 在機床切削狀態分類中，具有相同切削參數的振動信號通常被認為是同類數據。由于一些與切削參數無關的因素，如工件的切削位置、形狀和剛度會在加工過程中不斷變化，這會使系統的傳遞函數發生變化，最終導致同類數據的一致性差，樣本發散度高。(2) 在精加工中，不同切削狀態下的切削參數變化微小，從而使得t-SNE在特征空間中難以區分。在基于t-SNE的切削狀態分類的應用中，應主要關注多種物理感知信息的融合與嵌入。

近年來，越來越多的研究關注將標簽信息引入t-SNE以獲得更好的性能。文獻[17]引入了類標簽信息，提出了有監督的隨機鄰接嵌入方法，以捕捉內在結構。基于數據標簽的監督時間t-SNE[18]和深度監督t-SNE[19]被提出，來提取特征并學習數據的內在關系。在制造過程中，除了常用的振動信號，還有許多物理信息，如電流、力、坐標信息等都可以被測量，并作為信息嵌入。因此，本文旨在采用切削激勵點的空間坐標嵌入t-SNE，以提取出更有區分度的特征，從而提高削狀態分類的準確率。

本文提出了一種空間坐標嵌入的流形學習方法，基于振動信號構建高維特征空間，利用切削激勵點的空間坐標修正樣本分布，對機床的切削過程進行建模，命名為空間坐標嵌入的t-SNE(spatial coordinate embedded t-SNE, Ct-SNE)。Ct-SNE減小了振動特征空間中類內數據的差異，將相同切削參數的數據在高維空間中緊湊分布，以獲得區分度更高的低維輸出。在一臺三軸立式銑床上進行了試驗研究，收集了機床在多種切削狀態下的振動信號和空間坐標作為數據集，對t-SNE和Ct-SNE的性能進行了比較和討論。

1 t-SNE算法基本理論

由于高維特征池存在冗余信息，導致同類數據的一致性較弱，異類數據的相似成分過多，無法準確地反映機床的狀態信息。因此需要對特征進行降維，選擇出與切削狀態密切相關的敏感特征，以提高狀態分類的準確性。流形學習是一種基于拓撲流形概念的降維方法，可保留數據的本質結果，適合描述非線性過程，被用于特征選擇。首先對流形學習中的t-SNE理論進行簡單的回顧。

X={x1,x2,…,xn}?RD×n代表n個D維向量，作為t-SNE的輸入，Y={y1,y2,…,yn}?Rd×n代表t-SNE處理后的低維輸出。

對輸入X，采用基于高斯分布定義的成對相似度pij表示樣本間的相似關系，計算過程如下

(1)

式中：xi和xj是X中的樣本;σi是xi的方差。

t分布用于描述低維數據的成對相似度，計算過程為

(2)

最終的輸出Y由最小化概率分布P和Q之間的Kullback-Leibler散度獲得，代價函數被定義為

(3)

2 空間坐標嵌入的t-SNE

對分類任務而言，有效的特征會將類內距離最小化，類間距離最大化。在本文的研究中，切削參數(包括主軸速度，進給速度，切削深度，刀具類型等)相同的狀態被視為同一類別。振動信號雖包含豐富的信息，可以構建特征空間描述切削過程，但使用傳統的無監督方法t-SNE難以捕獲振動信號不同工況間的細微差異，使不同類別的特征在低維空間中產生交疊現象，最終使準確分類變得困難。且振動模式受到切削位置的影響較大，使樣本發散程度高，不利于分類識別。為了獲得更有效的特征，本文提出了一種空間坐標嵌入的t-SNE算法(spatial coordinate embedded t-SNE, Ct-SNE)，將切削激勵點的空間坐標作為監督信息引入到振動信號構建的特征空間中。

如公式(1)所示，t-SNE使用歐幾里德距離表示樣本之間的相似性。它遵循原始數據分布，沒有任何監督信息。

數據xi和xj的歐幾里德距離被定義為

(4)

為了提高t-SNE在特征選擇時的有效性，Cheng提出了有監督的t-SNE的框架用于更精準的特征選擇。其基本思想是使同類樣本在特征空間中更接近，根據類別標簽定義了樣本間距離修正項

(5)

式中：τ∈(0,1)是一個常數參數是一個常數參數，表示縮小歐氏距離的尺度；c代表樣本的類別。由公式(5)可知，同類點的距離按τ尺度被縮減，以強制增加樣本間的相似度。異類樣本間的距離沒有變化，以保持原始分布。

在此方法基礎上，本文結合切削過程，引入切削激勵點的坐標至振動信號構成的特征空間，將修正項常數τ修改為與切削激勵點的坐標相關的變量，以獲取更高的靈活性，使類內樣本的距離減小，而類間樣本的距離增大。銑削過程為刀具作用在工件上的若干個連續沖擊，是一個復雜的非線性過程[20]。其動態特性受多重因素影響，例如：工件的裝夾位置、夾緊力度、激勵點位置變化等。對銑削過程的振動分析通常是將工件劃分為若干個微元體，并視同一個微元體的振動模態是相同的[21]。因此當刀具位置變化為小量時，振動信號聲學特征的變化量可近似看成線性相關的，有較強的相似度。這里合理地假設來自相同切削參數的振動信號有著相似的基本分布，且切削激勵點位的變化越小，振動信號的差異越小。為了使相同切削參數的樣本具有更集中的分布，本文參考文獻[22]，定義了基于切削點空間坐標的距離修正項

(6)

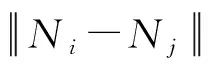
(7)

(8)

低維空間中的相似性和損失函數與t-SNE相同，如公式(2)和(3)中所示。

Ct-SNE算法的流程圖如圖1所示。首先使用振動信號構建高維特征集，并計算特征樣本間的歐幾里德距離；使用切削激勵點的空間坐標計算距離修正項。結合歐氏距離和距離修正項計算高維樣本間的相似度，并得到隨機初始化的低維輸出。之后使用Kullback-Leibler散度作為代價函數，迭代優化低維輸出，最終得到最優的低維輸出。

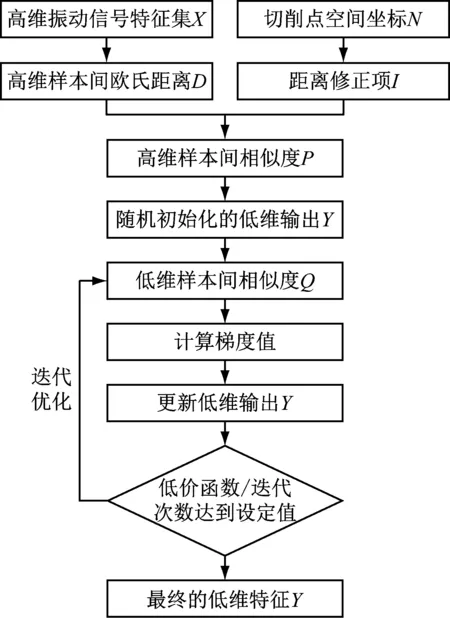
圖1 空間坐標嵌入的t-SNE流程圖

3 試驗與分析

3.1 機床切削狀態監測方法框架

機床切削狀態分類系統可為加工過程提供有價值的信息，使用物理感知與數據驅動結合的方法，可以得到機床真實的切削參數，保證機床正常加工。其性能取決于它使用測量信號對不同切削狀態分類識別的能力，狀態監測的整體流程如圖2所示。首先進行信號采集，采集的信號可以反映有關機械元件動態過程的信息，然后進行數據預處理，主要包括去除靜默段信號、濾波、分幀和標注樣本。再通過時域和頻域中的分析方法對信號分析和特征提取，使用流形學習對高維特征進行特征選擇。最終使用適當的分類器實現對當前狀態的切削參數的識別。

圖2 切削狀態分類流程圖

3.2 數據采集

參照圖3，數據采集試驗是在VCM640三軸銑床上實施的，采集到了機床在不同的切削狀態下的振動信號和空間坐標。機床上放置了一個加速度計來采集振動信號，三個光柵尺來采集X、Y和Z方向的位移變化。圖3所示的光柵尺采集的是機床導軌X方向的位移，還有兩個光柵尺分別平行安裝于機床導軌Y方向和主軸Z方向。振動信號的采樣頻率為32 kHz，切削空間坐標的采樣頻率為1 kHz。關于采集到的振動信號和切削空間坐標的簡要的介紹如下。

圖3 數據采集示意圖

(1) 振動信號。一個加速度計被放置在銑床的夾具上來收集振動信號。加速度計的頻率響應在30Hz～10 kHz。加速度計被磁座固定在夾具上，該位置與切削點之間的傳輸路徑短，且保證了剛性傳輸，使獲取的信號的信噪比高。經過時域和頻域分析，振動信號在本文中被提取為高維特征池。

(2) 切削點的空間坐標。切削空間坐標是由三個光柵尺測量得到的。兩個光柵尺垂直安裝在機床導軌下側，用于收集X和Y方向的切削坐標；一個光柵尺與主軸平行放置，用于收集Z軸坐標。三維坐標表示真實空間中的切削位置，并被用作特征選擇方法的嵌入信息。

3.3 數據描述

本文的試驗的參數設置如表1所示，銑床以不同的切削狀態加工鋁制工件，刀具為硬質合金立銑刀。每次加工沿著X正方向進行。毛胚的每一層可以進行多次完整的加工。

表1 銑削試驗設置

7類狀態的切削參數如表2所列，其中變化了不同的切削深度、主軸轉速、進給速率和刀具類型。相同的試驗被重復五次，每次加工包括入刀、穩定切削和出刀。

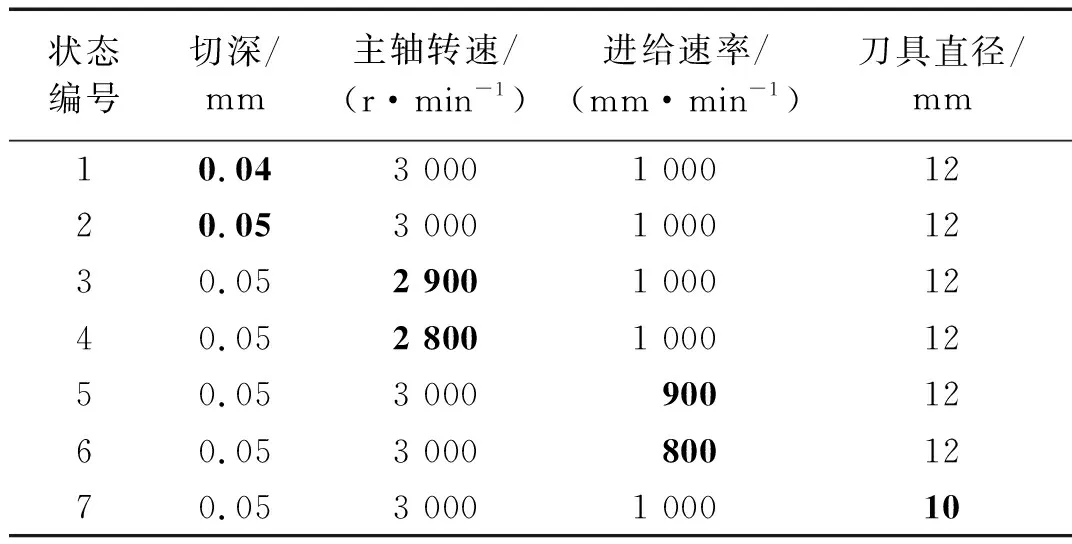
表2 不同切削參數下的切削狀態

3.4 數據預處理

為保證信號的有效性，在信號采集后，使用巴特沃斯濾波器實現對振動信號進行30 Hz～5 kHz帶通濾波。去除掉刀具與工件剛接觸時產生的巨大沖擊和未切削的靜默段后，對有效切削信號進行分幀并標注。一個樣本的時間長度為500 ms，步長為100 ms，每個切削狀態包含3 000個樣本。

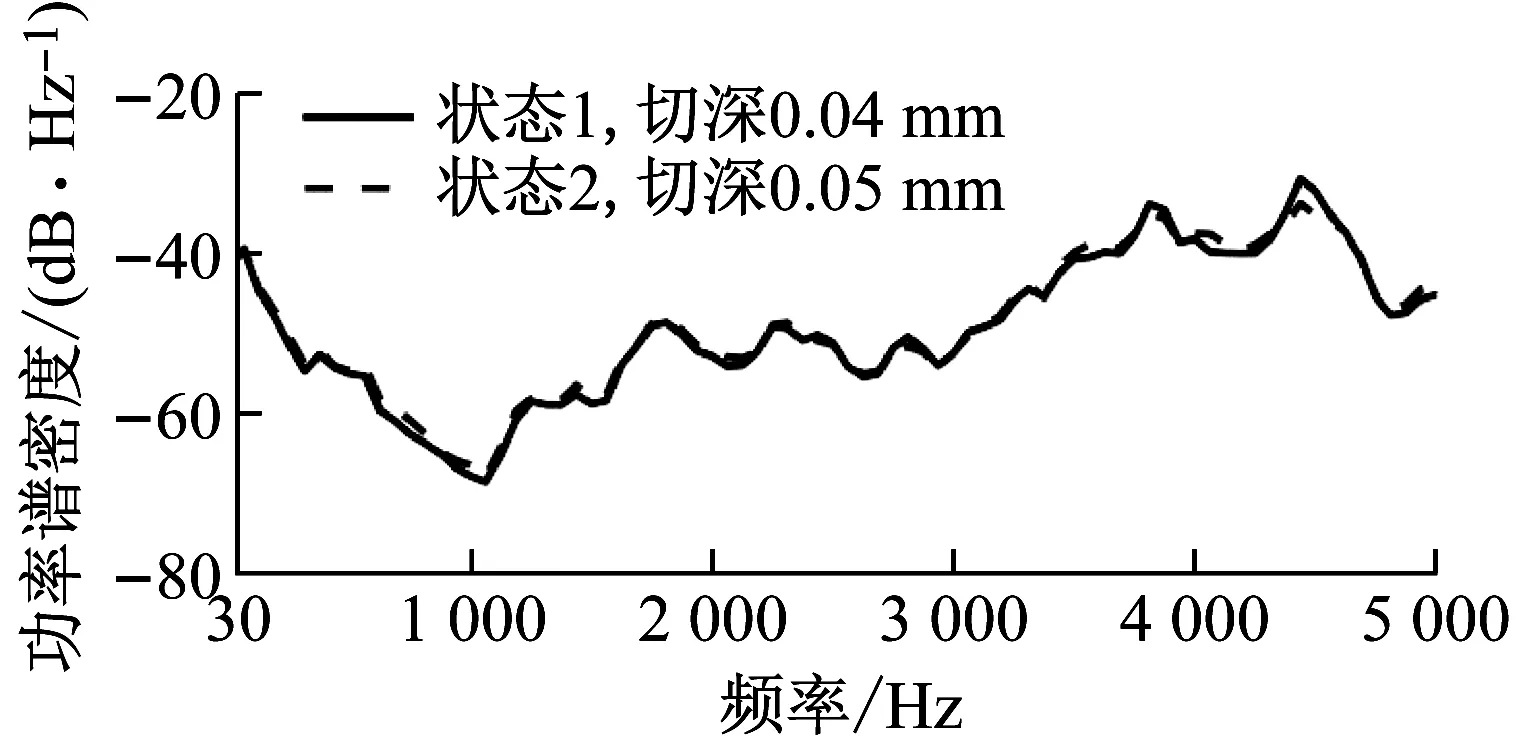
圖4繪制了每類狀態一次完整的切削過程的振動時域圖，包括入刀、穩定切削和出刀。入刀時，刀具與工件的接觸由點逐漸變成半圓弧；當切削長度大于刀具的半徑r時，刀具與工件的接觸范圍為半徑r的半圓弧，之后的加工為穩定切削；出刀時，刀具與工件的接觸逐漸從半圓弧變為一個點，直至刀具徹底離開工件。圖5繪制了不同切削狀態的功率譜密度。圖4(a)繪制切削深度變化的振動信號時域圖，不同切削深度的信號幅值差異很微弱。從頻域圖5(a)中，兩種切削深度的功率譜密度曲線擬合程度很高，僅在3 500～4 500 Hz存在微弱差異。圖4(b)、圖5(b)繪制了不同主軸轉速的信號圖，可以看出在30～200 Hz內，低轉速的功率譜密度值較大，在3 000～3 500 Hz內，高轉速的功率譜密度值較大。圖4(c)繪制了進給速率為800 mm/min和900 mm/min的振動信號時域圖，該圖顯示了不同進給速率在固定長度的工件上進行完整切削一次的信號，由于狀態6的進給速率小于狀態5，因此使用切削狀態6完成固定長度的切削需要花費更多的時間。在其頻域圖5(c)中，在3 000～5 000 Hz范圍內，兩狀態有一定區分度。圖4(d)、圖5(d)繪制了不同直徑的刀具對應的切削信號圖，由于刀具直徑差異較大，振動信號在時域、頻域有著較高的區分度。從信號圖可以看出，曲線的變化關系并不是線性的，這是由于機械加工是一個動態的非線性過程。機床由許多部件組成，如轉子、軸承、齒輪等。每個部件都有幾個獨立的自由度，當改變某種切削狀態時，一個部件的變化會影響到更多部件的狀態，因此在測量信號中會出現非線性耦合，信號隨某種參數的變化并不是單調的。

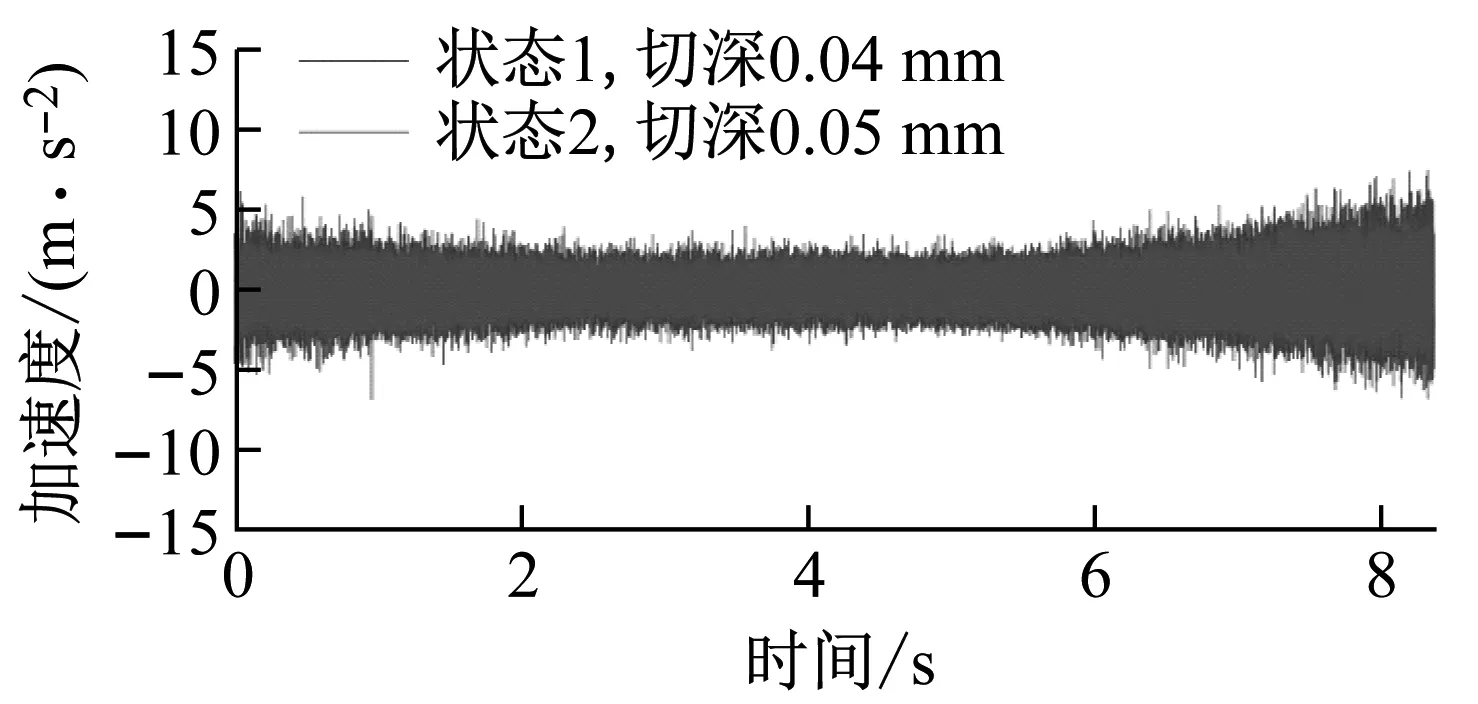
(a) 不同切削深度

(a) 不同切削深度

另外，從時域圖4中可以看出，每一次連續的切削過程都包括了入刀、穩定切削和出刀。入刀和出刀時的振幅大于穩定切削時的振幅。

圖6繪制了由光柵尺采集到的狀態2的六次切削過程的坐標變化情況。坐標變化與實際情況一致，沿著Y方向的反方向在X和Z方向上做六次往復運動。

3.5 特征提取

在制造過程中，加工狀態種類的多樣性和實測信號的隨機性對機床狀態分類是一項挑戰。單一的特征可能不足以精準描述加工過程，確切的最佳特征是事先不知道的。因此，需要從振動信號中提取不同的時域和頻域特征以生成高維的特征池，然后使用特征選擇方法選擇出有效的特征子集。對振動信號X={x1,x2,…,xn}?RD×n，本文選擇了常用的十一種時域和頻域特征來描述機械加工狀態[23]，構成了高維的特征池。

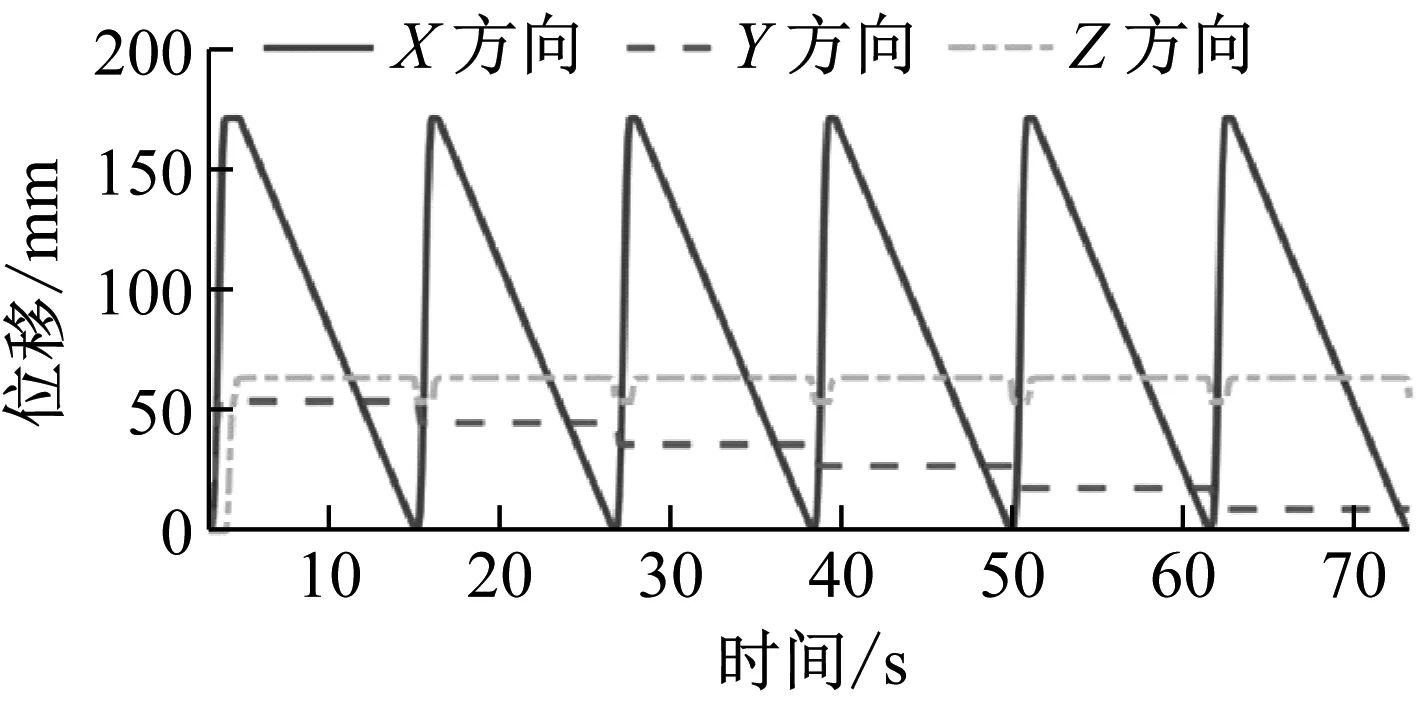
圖6 連續六次切削X、Y、Z軸位移變化圖

表3 由振動信號提取的特征

式中，p(f)為信號的功率譜。為了消除特征間單位和尺度差異的影響，本文對特征集進行了歸一化處理，將特征值轉化到值域空間[0,1]上。

4 結果與討論

為了驗證特征選擇方法的有效性，本節進行特征可視化試驗和分類試驗來分析比較Ct-SNE與傳統方法t-SNE的性能。

4.1 可視化試驗

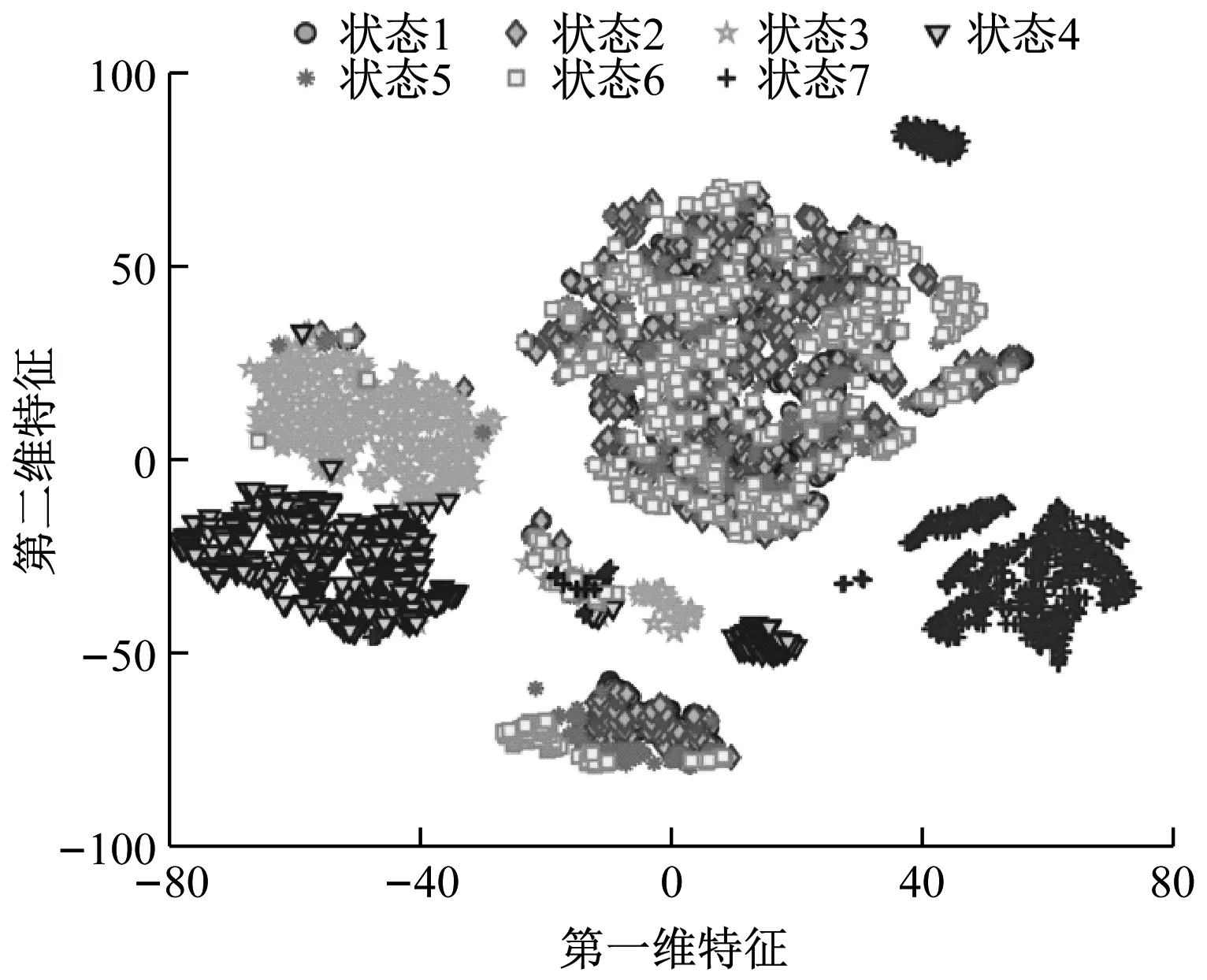
可視化試驗比較了t-SNE和Ct-SNE在二維空間中的結果。這兩種方法的參數按照文獻[12]建議設置如下，困惑度設為經驗值30，迭代次數t設置為1 000，動量項α(t)設置為0.8，學習率η初始設置為100，并在每次迭代后，它都會根據自適應學習率方案[24]進行更新。對振動信號提取的特征和光柵尺采集到的坐標信息做最大最小歸一化。七類切削狀態的二維嵌入結果如圖7所示，其中每一個點代表一個樣本，相同顏色相同標記的點來自一類切削狀態。

(a) t-SNE的二維嵌入結果

從圖7(a)的結果可以看出：(1) t-SNE的二維結果混疊嚴重，變化切削深度和進給速率的狀態(狀態1、2、5、6)在二維空間區分度低。這是由于不同狀態的參數差別很小，其振動特征相似性較高，大部分類別的樣本在特征空間中區分度不大。狀態3、4對應了不同的主軸轉速，區分度高于不同切深的狀態；因為狀態7的刀具直徑與其余狀態相差較大，因此狀態7也可以被有效區分。(2) 每個類別的樣本發散程度高，形成多核聚類的現象。這是由于每一次完整的切削都包括入刀、穩定切削和出刀三個過程，參考圖4可以得知，入刀和出刀的振幅明顯大于穩定切削的振幅，因此入刀和出刀過程的數據與穩定切削的數據存在差異，在低維空間中被聚成了多簇。

圖7(b)中Ct-SNE的結果顯示，不同切削參數的特征區分度明顯提高，類內特征的發散程度降低。這是因為切削激勵點的空間坐標嵌入的的Ct-SNE方法在振動信號構成的特征空間中拉近了同類別特征的距離，使同類數據的相似度提高，從而使同一類別的數據分布更加緊湊。Ct-SNE算法可以使不同切削狀態的區分度提高，因此可以考慮將Ct-SNE作為特征處理方用于機床切削狀態分類。

4.2 最優維度選取

本文用到的特征選擇方法t-SNE和Ct-SNE都涉及目標輸出維度d。3.1節為了可視化結果更直觀，將d的值設定為2。事實上，d對分類結果至關重要，因為如果d太小，會丟失太多的有效信息，而d太大，冗余或不敏感的特征會被保留。在分類試驗中，K近鄰算法被用于數據分類，按照經驗將K近鄰算法中的近鄰數K設定為30，以獲得不同d值的分類精度。使用10折交叉驗證的方法。圖8顯示了t-SNE和Ct-SNE方法在不同維度上分類準確率。

圖8 目標維度d對分類準確率的影響

在圖8中，橫軸代表不同維數的特征，縱軸代表分類準確率。t-SNE在四維特征上達到最佳分類準確率57.96%，Ct-SNE在五維特征上達到最佳準確率，準確率為96.78%。并且分類的結果與可視化結果一致，Ct-SNE在對特征進行非線性維數約減時有比t-SNE更好的表現。

4.3 特征選擇算法用于切削狀態分類

基于t-SNE和Ct-SNE的特征選擇方法并不像線性降維方法那樣提供從高維到低維空間的明確映射。然而，這一步對于機床狀態分類是非常重要的，因為它必須處理訓練樣本集以外的新數據，這也被稱為增量學習問題。迭代新增樣本嵌入算法[25]被引入來解決增量學習問題。該方法先對新增樣本進行局部線性重構，再通過迭代優化的方式優化低維輸出特征。

為驗證分類性能，引入了精度Precision(Pre)、召回率Recall (Rec)、F1-score(F1-Scr)和準確率Accuracy (Acc)四個指標[26]來評價這些特征選擇方法的分類性能。分類設置與3.2節一致。在每種特征選擇方法的最優維度上進行分類試驗，這些性能指標在測試集中的結果如表4所示。

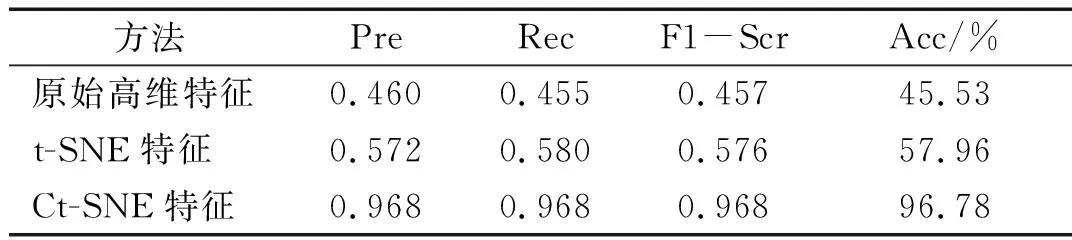
表4 不同方法分類評價指標

這四個評價指標的數值越大，意味切削狀態分類的性能越好。從表4中可以看出，原始特征的分類性能較差，這是由于不同狀態的差異較小，振動特征池中的冗余會干擾分類判決的準則。經過t-SNE選擇后的特征的分類性能有了一定的提升，可以達到57.96%，說明t-SNE可以一定程度上去除特征池中的冗余和非敏感信息。通過引入切削激勵點的的空間坐標，分類性能有了顯著的提升，各項指標都在96%左右。這說明在空間坐標的約束下，同類數據特征的一致性變強，異類特征的區分度變高，從而提升分類性能。

為了獲得更多分類結果的細節，圖9和圖10分別繪制了最優維度下的t-SNE特征和Ct-SNE特征的分類的混淆矩陣。

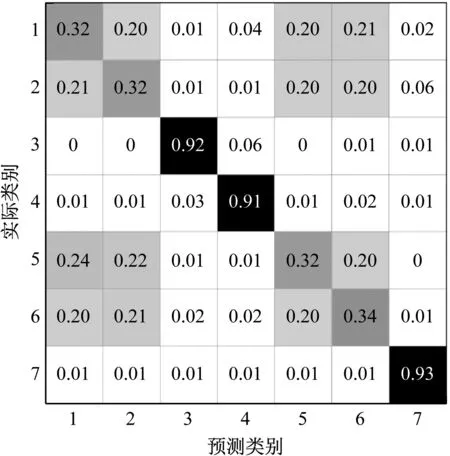
圖9 t-SNE的四維特征分類混淆矩陣

由圖9可見，狀態1、2、5、6的分類準確度很低，大部分數據被錯誤地分到了不同切削深度或不同進給速率的狀態中。這與可視化結果圖7(a)一致，在僅使用振動信號時，不同切削深度和不同進給速率的數據在特征空間中難以區分，因此分類的錯誤率較高。而不同的主軸轉速如狀態3、4，與不同刀具直徑如狀態7，有較高的分類準確性。

圖10顯示了Ct-SNE的五維特征的分類的混淆矩陣。整體來看，分類準確性有了大幅度提升，各類別狀態的分類準確率都達到94%以上。部分錯誤的分類是由特征解耦不徹底，數據存在少量混疊。例如狀態1的部分數據被錯分為狀態2。狀態5的少量樣本落入了狀態3的數據分布內。整體結果說明切削激勵點的空間坐標的加入，對區分振動信號構成的特征起到了促進作用。

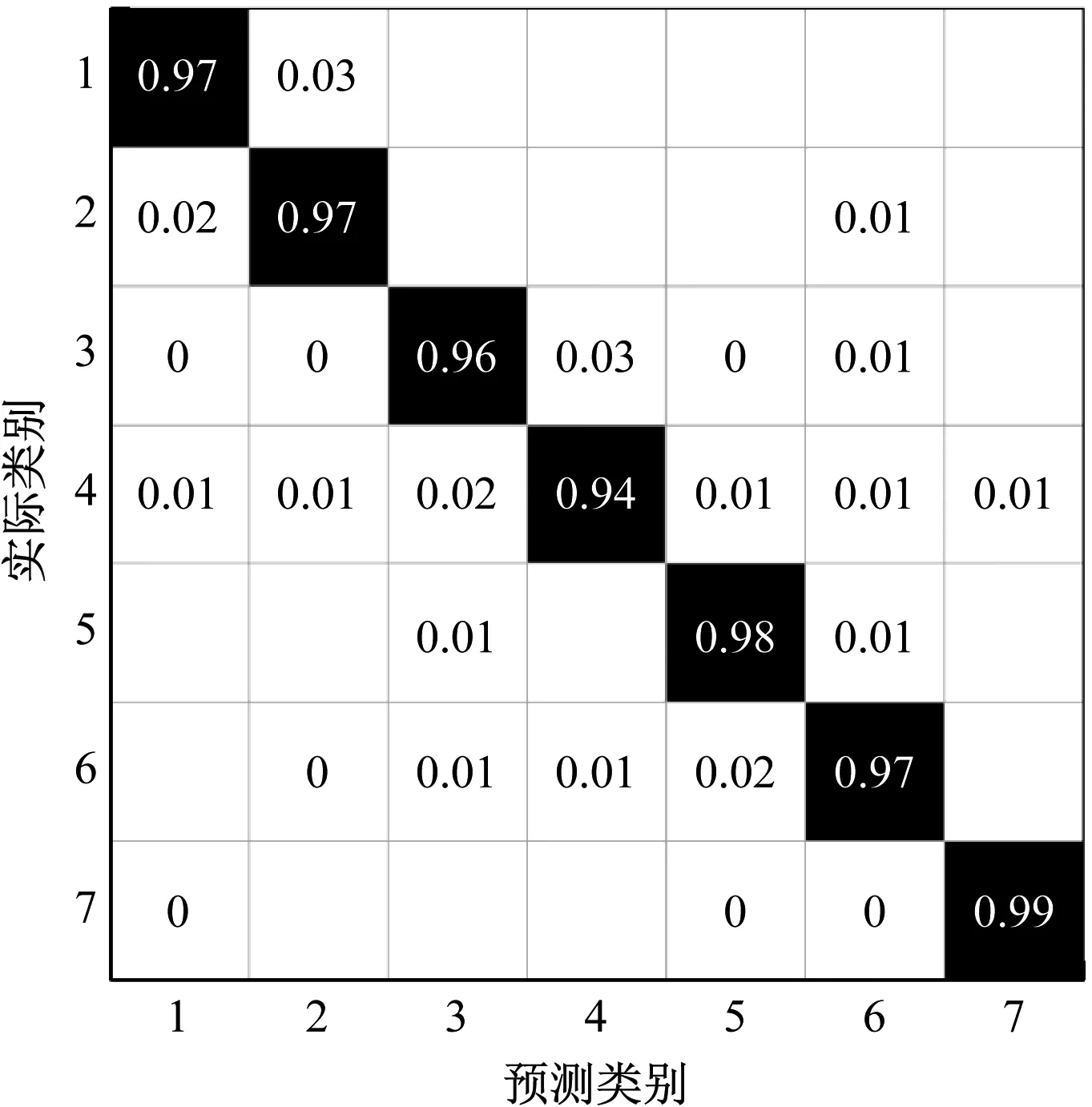
圖10 Ct-SNE的五維特征分類混淆矩陣

5 結 論

為了提高切削狀態分類的精度，本文融合振動信號特征與切削點的空間坐標，提出了空間坐標嵌入的t分布的隨機鄰域嵌入方法Ct-SNE，以選擇有效特征用于機床切削狀態分類。針對特征可視化結果和分類性能的評價標準展開分析，得到以下結論：

(1) Ct-SNE將切削空間坐標嵌入振動特征空間，構建了距離修正項，使類內數據分布更緊湊。從特征可視化的結果和分類性能的角度分析，該方法可提高不同切削參數振動特征的可區分度，進而狀態分類的準確性，并優于無監督的流形學習方法t-SNE。

(2) 合適的目標特征維數可以獲得更高的狀態分類準確率。若維數過低，則損失過多有效信息，若維數過高，過多冗余會影響分類。

基于本研究所提出的空間坐標嵌入的t-SNE算法框架，將進一步開展多傳感信號與加工狀態的關聯研究，獲得更多維度的信息，以提升機床狀態分類的準確率。