基于復合材料理論的再生混凝土峰值應變模型

趙木子 ， 王玉銀 ， 耿 悅

（1.中冶建筑研究總院（深圳）有限公司，廣東深圳 518055；2.哈爾濱工業大學（深圳）土木與環境工程學院，廣東深圳 518055；3.哈爾濱工業大學結構工程災變與控制教育部重點實驗室，黑龍江哈爾濱 150090；4.哈爾濱工業大學土木工程學院，黑龍江哈爾濱 150090）

通過調整混凝土配制時的用水量［1-3］、優化骨料顆粒級配［4-5］和添加鋼纖維［6］等方式，可以有效降低再生骨料的影響，使再生混凝土（RAC）的性能滿足建筑結構的要求.可靠的再生混凝土軸壓應力-應變模型是進行再生混凝土結構設計的前提，而準確預測再生混凝土的峰值應變（峰值應力對應的應變）是建立該模型的關鍵.同時，再生混凝土的峰值應變也是評價其變形能力的重要參數，應予以研究.當再生骨料摻入時，由于表面存在殘余砂漿，降低了再生骨料的剛度，使其對新砂漿變形的約束作用下降，峰值應變增大［7-9］.前期研究已發現，再生骨料表面殘余砂漿的含量及制作再生骨料的原混凝土水灰比（基體混凝土水灰比）會影響骨料的剛度［2，10］，是峰值應變的關鍵影響因素.因此，在再生混凝土峰值應變模型中應考慮上述關鍵因素的影響.

為此，本文首先基于收集到的100 組再生混凝土峰值應變數據，充分論證傳統再生混凝土峰值應變模型的局限性；隨后，在復合材料模型的基礎上，考慮再生骨料的影響，通過理論推導建立考慮殘余砂漿含量及基體混凝土水灰比影響的峰值應變預測模型；最后，通過參數分析與試驗數據對比，確定了形式較為簡單且預測精度較高的預測模型.

1 傳統再生混凝土峰值應變模型的局限性

目前，各國學者已考慮再生骨料摻入的影響，對再生混凝土峰值應變預測模型開展了研究，針對加載方式［11］、取代率［12-14］、骨料類型［15］、混凝土強度［16-17］、骨料碳化程度［18］和受火溫度［19］等關鍵因素的影響建立了模型.研究中所采用的建模方法主要分為2種.一種是沿用現行規范中普通混凝土彈性模量模型的建模方式，以再生混凝土強度為主要參數，通過試驗回歸方法建立模型（如文獻［11］）.這類模型公式簡單，易于被設計人員采納.另一種是以再生粗骨料取代率為主要參數（如文獻［13，16-17］）建立模型.盡管現有文獻顯示前一種方法對各自的試驗均具有良好的預測精度，但由于這類模型均基于有限的試驗數據建立，試驗數據參數范圍較窄且各文獻的試驗參數也不相同，因此在預測較廣參數范圍內再生混凝土的峰值應變時可能具有局限性.

因此，本節將主要討論現有建模方法在預測收集到的100 組較廣參數范圍峰值應變數據時的可靠性，為后文再生混凝土峰值應變模型的建立奠定基礎.

1.1 與混凝土強度相關的模型

為評估傳統混凝土峰值應變建模方法在預測再生混凝土峰值應變時的可靠性，對所收集到的12 篇文 獻［5，7，9，15-17，19-24］中 100 組 再 生 混 凝 土 峰 值 應 變 εc0，r數據與混凝土28 d 圓柱體軸心抗壓強度fcm28之間的關系進行分析，結果如圖1 所示.圖中所涉及的試件涵蓋了工程中常見的再生混凝土參數范圍：再生粗骨料取代率（質量分數，文中涉及的取代率、水灰比等除特別說明外均為質量分數或質量比）為0%～100%，再生細骨料取代率為0%～100%，殘余砂漿含量為5.5%～40.0%，28 d 圓柱體軸心抗壓強度為19.1～89.2 MPa.由圖1 可以看出，具有相同圓柱體軸心抗壓強度試件的峰值應變離散性較大.例如，當混凝土強度等級為C30 時，再生粗骨料混凝土峰值應變在（1 523～4 449）×10-6范圍內波動，差異高達192%；再生細骨料混凝土峰值應變范圍為（1 484～2 974）×10-6，差異為100%.造成該差異的主要原因在于再生骨料對混凝土強度與其對峰值應變的影響機理不同.具體而言，混凝土強度主要受有效水灰比及界面過渡區黏結性能的影響，目前大部分試驗采用預吸水法或飽和面干法處理再生骨料，致使再生骨料內部的相對濕度高于新水泥漿，在混凝土拌和過程中，骨料內預吸附的自由水會向外擴散，從而增大混凝土的有效水灰比［2］；同時，再生骨料的摻入會降低骨料-新水泥漿間界面過渡區的黏結強度［8］.而再生骨料對峰值應變的影響主要體現在混凝土裂紋劇烈開展導致的砂漿變形提高以及骨料自身剛度的降低.此外，再生骨料影響機理的差異可導致再生骨料對混凝土 fcm28及 εc0，r的影響趨勢不同 .例如，在文獻［9］中，100% 摻入再生粗骨料將使 fcm28降低 6.5%，εc0，r提高20.2%.由于傳統模型通常認為混凝土強度與峰值應變的變化趨勢相同，因此采用傳統建模方法無法準確預測再生混凝土的峰值應變，具有局限性.

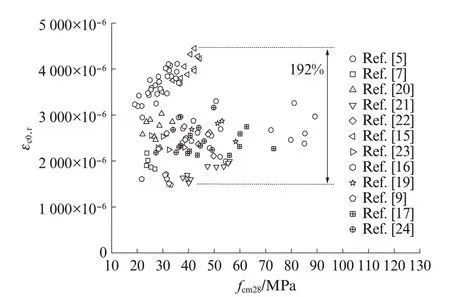
圖1 再生混凝土峰值應變與強度的關系Fig.1 Relationship between εc0，r and fcm28 of RAC

1.2 與再生粗骨料取代率相關的模型

近年來，各國學者［13-19］以再生粗骨料取代率rC為主要參數，通過建立再生混凝土與同配比普通混凝土峰值應變之間的關系來量化再生骨料的影響.為分析該方法的準確性，對再生混凝土與同配比普通混凝土峰值應變的比值（εRAC0/εNAC0）同rC之間的關系進行對比分析，如圖2 所示.圖中所采用數據點的參數范圍與圖1 相同.由圖2 可見，盡管以再生混凝土與同配比普通混凝土峰值應變之比來量化再生骨料影響的建模方式，可以在一定程度上降低試驗結果的離散性（再生混凝土峰值應變試驗結果離散性由192%下降至81%），但再生骨料的影響因素較多，僅以rC為主要參數建立模型仍無法準確描述再生混凝土的峰值應變，可能需要引入基體混凝土水灰比mWor/mCor、殘余砂漿含量wRM等影響參數.例如，將文獻［5，15，24］中基體混凝土水灰比與殘余砂漿含量不同的典型試件試驗結果進行對比，如圖3 所示.

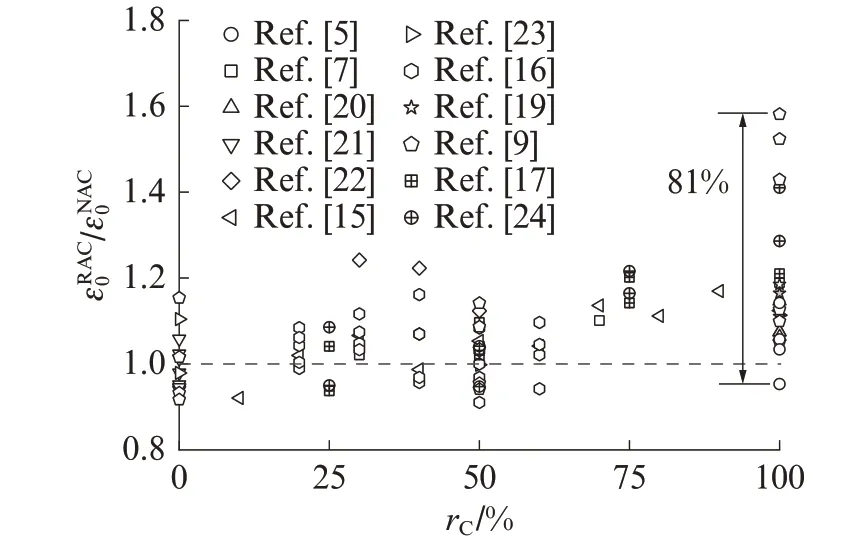
圖 2 εRAC0 /εNAC0 與 rC的關系Fig.2 Relationship between εRAC0 /εNAC0 and rC

從圖3 中可以看出：基體混凝土水灰比和殘余砂漿含量也是影響混凝土峰值應變的關鍵因素，當基體混凝土水灰比從 0.56 下降至 0.28 時，εRAC0/εNAC0值可降低49%（圖3（a））；當殘余砂漿含量從5.5%提升至34.7%時，εRAC0/εNAC0隨著再生粗骨料取代率的變化而顯著變化，在再生粗骨料全取代條件下二者差異可達23%（圖3（b））.造成該顯著差異的原因在于基體混凝土水灰比的提高以及殘余砂漿含量的降低均會使得骨料剛度減小，導致骨料對新砂漿變形的約束作用減弱，峰值變形增加.

圖3 不同基體混凝土水灰比及殘余砂漿含量的典型峰值應變數據對比Fig.3 Comparison of strain at peak stress for salient RAC with different m/m and w［5，15，24］WorCorRM

綜上，以rC為主要參數的傳統建模方法無法準確描述由基體混凝土水灰比及殘余砂漿含量變化引起的再生骨料影響差異，具有局限性.

2 基于復合材料理論的再生混凝土峰值應變模型

文獻［9］基于 Zhou 等［26］提出的復合材料理論（Reuss 模型），將再生混凝土視為由天然粗骨料、再生細骨料、殘余砂漿和新砂漿組成的體系，并且認為再生骨料中殘余砂漿與原天然骨料變形之間的關系也滿足復合材料理論，采用再生混凝土與同配比普通混凝土峰值應變之比（kε-X=εRAC0/εNAC0，表示在“X”模型中εRAC0/εNAC0的數學描述）量化再生骨料的影響，建立了再生混凝土峰值應變的數學描述，如式（1）所示.

式中：εNAC0、εNACg0與εNACm0分別為當普通混凝土（NAC）軸向應力達到峰值應力fNACc時混凝土、天然骨料及砂漿的縱向應變；VNACCNA與VNACNM分別為普通混凝土中天然粗骨料與新砂漿的體積分數；εRAC0、εRACg0、εRACm0與εRACm0，r分別為當再生混凝土軸向應力達到峰值應力fRACc時混凝土、天然骨料、新砂漿與殘余砂漿的縱向應變；VRACTCNA、VRACNM與VRACRM分別為再生混凝土中總天然粗骨料（包括新天然粗骨料及再生粗骨料中的原天然粗骨料）、新砂漿和殘余砂漿的體積分數.

為對比所有常見復合材料模型［26］在預測再生混凝土峰值應變時的預測精度，本文沿用文獻［9］模型的推導方法，建立了不同復合材料模型中εRAC0/εNAC0的數學描述，如式（2）～（4）所示.

根據文獻［25］的建議，VRACTCNA、VRACNM與VRACRM可由式（5）～（7）計算.

在百雀羚產品線結構中，除了“天然不刺激”護膚綠之外，還有零售價4元的百雀羚鳳凰甘油，以及個人護理系列花露水等非核心產品。同時男士系列也是剛性不足，削弱了百雀羚的品牌屬性定位。引領百雀羚飛速發展的新生力量是草本系列，凈化品牌旗下的產品也許是百雀羚下一步要做的工作。不可否認，基于現實銷售規模等因素的影響，百雀羚目前仍沒有淘汰與品牌屬性定位不兼容的老品，未來產品線結構如何進一步優化提升，對于品牌操盤者是考驗。

式中：Eg為骨料的彈性模量，MPa；ENACm，sec為當普通混凝土軸向應力達到峰值應力時新砂漿的割線模量，MPa；ERACm，sec、ERACrm，sec分別為當再生混凝土軸向應力達到峰值應力時新砂漿、殘余砂漿的割線模量，MPa；VRACCA為再生混凝土中所有粗骨料的體積分數.

在混凝土加載過程中，骨料處于彈性階段，因此骨料的變形（εRACg0與εNACg0）分別表示為：

式中：σRACg0、σNACg0分別為再生混凝土、普通混凝土達到峰值應力時骨料所承受的應力，MPa；對于 Ruess 模型（串聯模型［26］）而言，二者為再生混凝土、普通混凝土的峰值應力；對于Counto模型而言，由于骨料、殘余砂漿、新砂漿呈現并聯 關 系［26］，因 此 σRACg0、σNACg0可 由 式（10）、（11）表示.

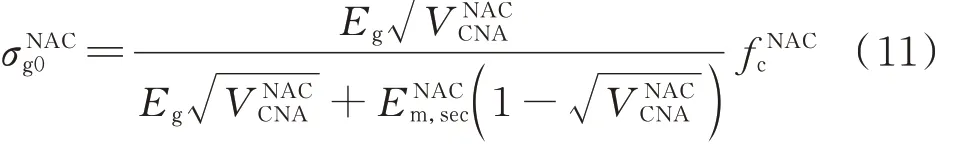
式（1）～（4）中砂漿的變形（εRACm0、εRACm0，r與 εNACm0）可以通過式（12）～（14）表示.

式中：σRACm0、σRACm0，r分別為再生混凝土達到峰值應力時新砂漿、殘余砂漿所承受的應力，MPa；對于Ruess 模型而言，二者均為fRACc；對于Counto 模型而言，通過骨料、殘余砂漿、新砂漿呈現的并聯關系［26］可以得到σRACm0、σRACm0，r的計算公式，如式（15）、（16）所示；σNACm0為當普通混凝土達到峰值應力時新砂漿所承受的應力，可由式（17）表示.

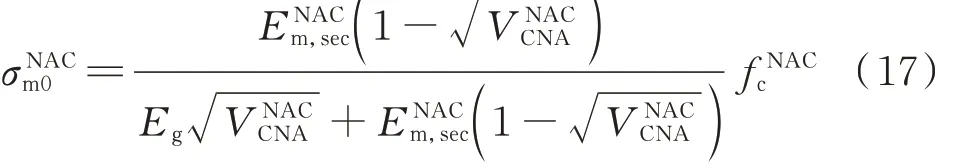
由上述模型的推導過程可知，再生混凝土、普通混凝土中砂漿的割線模量（即：ENACm，sec、ERACm，sec、ERACrm，sec）為關鍵計算參數，其取值應處于砂漿的彈性模量（Em、Erm）與 砂 漿 峰 值 應 力 所 對 應 的 割 線 模 量（Epeakm，sec、Epeakrm，sec）之間 . 根據 Kohee 等［27］的研究，砂漿峰值應力fm所對應的割線模量與其彈性模量之間存在如下關系：

本文采用新舊砂漿彈性模量（Em、Erm）與其峰值應變對應割線模量（Epeakm，sec、Epeakrm，sec）的平均值為再生混凝土和普通混凝土中砂漿的割線模量（即，ENACm，sec、ERACm，sec、ERACrm，sec）代表值進行計算，如式（20）～（23）所示 .據試算，砂漿割線模量在砂漿的彈性模量及其峰值應變對應割線模量間變化時，在常用混凝土水灰比（0.30～0.60）以及常用殘余砂漿含量（30.0%～50.0%）［2，17，28］范圍內，對再生混凝土與普通混凝土峰值應變之比計算結果的影響不超過5%.

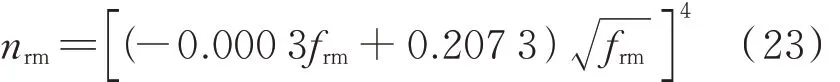
式中：mW/mC為再生混凝土的水灰比.

此外，基于文獻［30］，天然骨料彈性模量的取值范圍為69.0～88.7 GPa，砂漿彈性模量的取值范圍為15～31 GPa，因此：

將式（8）～（27）代入式（1）～（4）中，可以推導得出不同復合材料模型中εRAC0/εNAC0值的計算表達式：

式中：

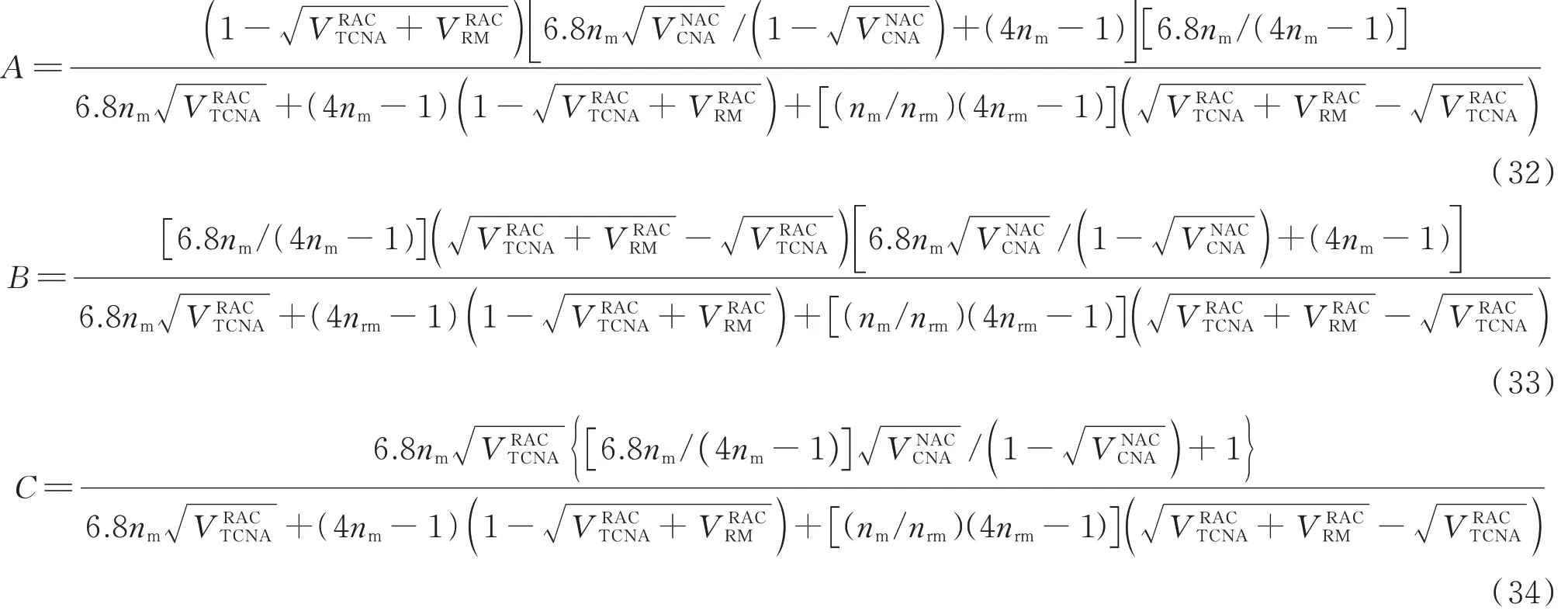
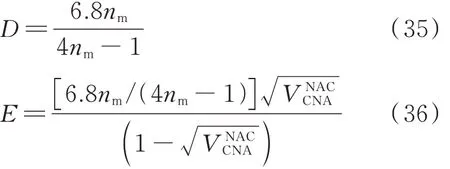
從式（28）～（36）可以看出，由不同復合材料模型推導的再生混凝土峰值應變計算模型差異較大，其中Voigt 模型和Ruess 模型較為簡單，而Hirsch模型和Counto 模型較為復雜. 為評估各模型預測結果的可靠性，下文將對上述模型進行系統參數分析，并將現有試驗結果與各模型的預測結果進行對比.

3 預測結果對比分析

3.1 參數分析

采用各再生混凝土峰值應變模型進行參數分析，結果如圖4 所示. 其中，殘余砂漿含量為20.0%～50.0%，基體混凝土水灰比為0.30～0.60，再生混凝土水灰比為0.45，再生粗骨料取代率為0%～100%，天然粗骨料與再生粗骨料的表觀密度再生骨料對峰值應變的影響.

從圖4 可以看出，隨著再生粗骨料取代率、殘余砂漿含量及基體混凝土水灰比的提高，再生骨料對峰值應變的影響逐漸增大，但增大幅度存在較大差異.例如，對于基體混凝土水灰比為0.30 且殘余砂漿含量為20.0%的混凝土，100%取代天然粗骨料將使峰值應變預測結果增大4.4%～8.6%；當基體混凝土水灰比增至0.45 且殘余砂漿含量為40.0%時，此預測結果將增大至15.2%～21.2%.

圖4 各模型峰值應變的計算結果對比Fig.4 Comparison of predictions for each peak strain model

各模型預測結果的差異也隨著再生粗骨料取代率、殘余砂漿含量和基體混凝土水灰比的增大而顯著增大. 例如，對于mWor/mCor=0.30 與wRM=20.0%的混凝土，當再生粗骨料取代率從25%增至100%時，各模型差異將由1.04%提高至4.2%（圖5（a））.當采用100%再生粗骨料且基體混凝土水灰比為0.30 時，殘余砂漿含量從20.0%增大至40.0%將使模型預測結果差異由4.2%提高至9.4%.當殘余砂漿含量為20.0%且再生粗骨料取代率為100%時，基體混凝土水灰比由0.30 增至0.60，各模型最大差異將由4.2%增大至31.7%.

3.2 基于試驗結果的模型對比

3.2.1 模型驗證

將所提出的再生混凝土峰值應變預測模型與收集到的 100 組現有試驗結果［5，7，9，15-17，19-24］進行對比，如圖5 所示.所采用的試驗數據基本涵蓋了工程中常用的再生混凝土參數范圍：再生粗、細骨料取代率為0%～100%、再生混凝土水灰比為0.25～0.65，基體混凝土水灰比為0.28～0.65，殘余砂漿含量為5.5%～40.0%. 需要說明的是，根據前期研究的建議［31］，除文獻［9，15，17，24］外，其余試驗中的基體混凝土水灰比結果均基于JGJ 55—2011《普通混凝土配合比設計規程》中抗壓強度與水灰比的關系表達式得到.由圖5 可以看出，當基體混凝土水灰比比再生混凝土水灰比高時，Voigt 模型的預測結果偏低，而Ruess 模型會高估再生骨料對峰值應變的影響，二者差異可達63.2%. 此時預測結果與試驗結果之比的 平 均 值 為 0.961～1.040，變 異 系 數（COV）為0.095～0.106.與前期對彈性變形的研究相似［25-26］，采用串、并聯模型結合的Hirsch 模型與Counto 模型，其預測精度較高，離散性較低.預測結果與試驗結果之比的平均值為0.978～1.000，變異系數為0.072～0.080.

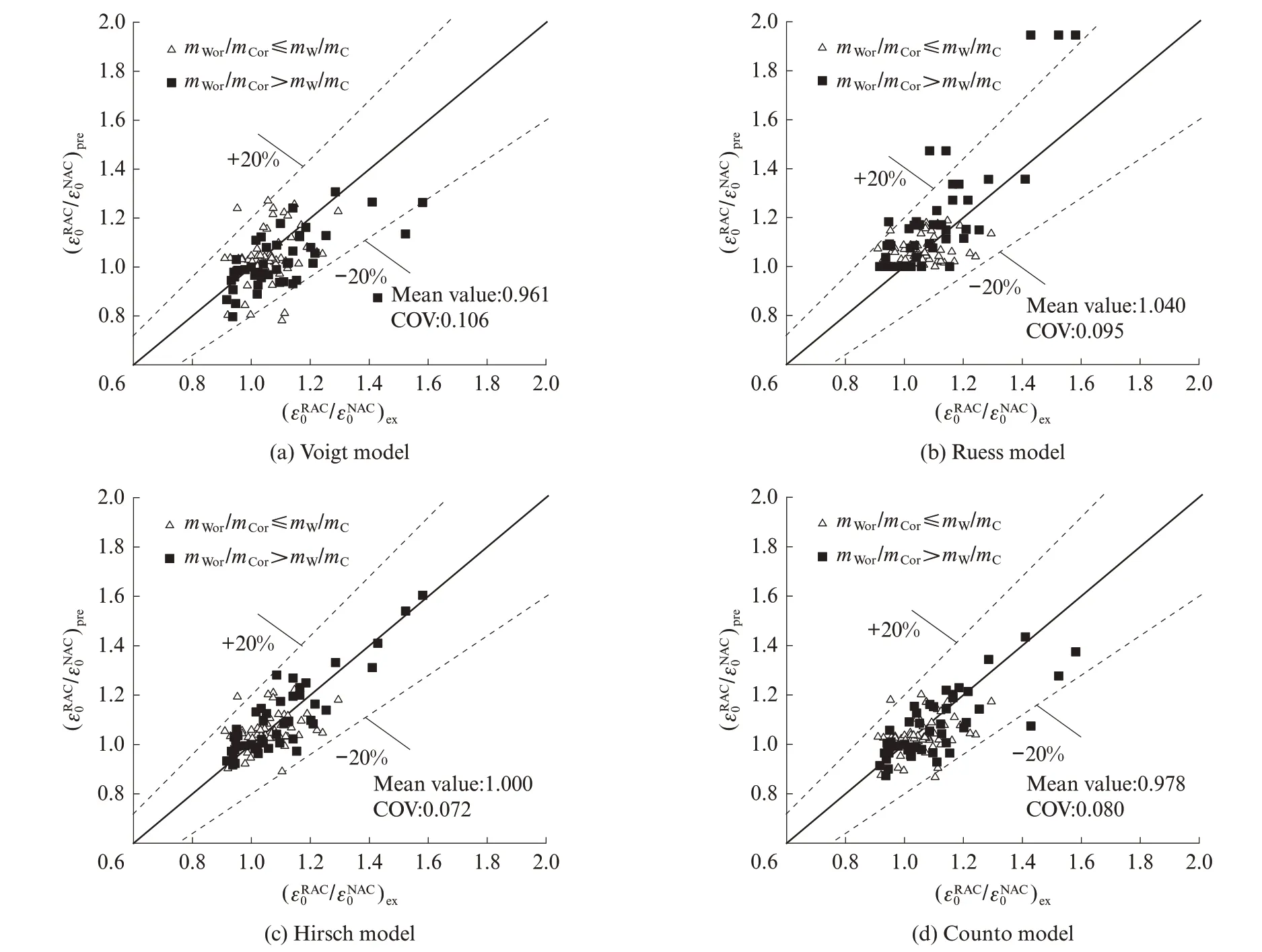
圖5 各模型預測結果與試驗對比Fig.5 Comparison of predictions and test results for each peak strain model

3.2.2 基體混凝土水灰比及殘余砂漿含量對預測精度的影響

為說明考慮基體混凝土水灰比及殘余砂漿含量影響的必要性，將本文模型（Hirsch 模型、Counto 模型）與不考慮上述影響因素的模型預測結果進行對比，如圖6 所示.圖中采用了基體混凝土水灰比較高與殘余砂漿含量較低（mWor/mCor＞mW/mC及 wRM＜20.0%）的典型試驗結果進行對比驗證.由圖6 可以看出，本文所提模型可較好地預測典型試件的測量結果，最大差異不超過10%.然而當不考慮基體混凝土水灰比及殘余砂漿含量影響時，模型則無法準確混凝土峰值應變，最大差異達45%.考慮到Counto 模型的表達式形式較為復雜，本文推薦采用Hirsch 模型來預測再生混凝土的峰值應變.

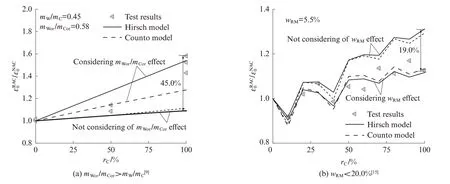
圖6 不同基體混凝土水灰比及殘余砂漿含量的典型試件預測峰值應變與試驗結果對比Fig.6 Comparison of predicted peak strain and measured results for salient RAC with different mWor/mCor and wRM

4 結論

（1）基體混凝土水灰比mWor/mCor和殘余砂漿含量wRM對再生混凝土峰值應變的影響顯著.對于100%取代再生粗骨料的混凝土，當mWor/mCor由0.56下降至0.28 時，再生骨料的影響幅度下降49%；當wRM由5.5%提高至34.7%時，該影響幅度增大23%.

（2）基于復合材料理論，采用理論推導方式建立了4 種可考慮mWor/mCor以及wRM影響的再生混凝土峰值應變模型.各模型預測結果的差異隨著再生粗骨料取代率、wRM與mWor/mCor的增大而顯著增大，差異可達31.7%.

（3）Hirsch 模型和Counto 模型的預測精度較高，離散性較低.特別是在預測基體混凝土水灰比較高與殘余砂漿含量較低（mWor/mCor＞mW/mC及 wRM＜20.0%）的混凝土時呈現明顯優勢，預測結果與試驗結果之比的平均值為0.978～1.000，變異系數為0.072～0.080.考慮到Counto 模型較為復雜，本文推薦使用Hirsch 模型進行預測.