基于Levenberg-Marquardt Feed-forward Back Propagation神經網絡的敏感性分析方法＊

姜強 劉天才 李宗洋 楊宏偉

（1.中國原子能科學研究院，北京 102413；2.中核戰略規劃研究總院，北京 100048）

引言

敏感性分析的目的是描述模型響應值受每個輸入變量或輸入變量組合不確定性的影響。有多種算法可用于進行敏感性分析。例如，計算輸入變量樣本與輸出樣本的相關性（基于相關性的度量）、模型在給定點的偏導數值（線性化方法）等。總的來說，敏感性分析算法可以分為三類：基于樣本的方法、線性化方法、全局方法。

（1）基于樣本的方法：基于對模型可用的蒙特卡羅樣本后處理，得到敏感性分析結果，不需要特殊的采樣方法。典型的方法有：輸入/輸出相關性方法（Input/output Correlation Method）、標準回歸系數方法（Standard Regression Coefficients Method）等。

（2）線性化方法：基于假設模型是線性并進行模型評估得到敏感性分析結果。此方法無法識別輸入變量之間的非線性行為和高階交互。典型的方法有：微擾法（Perturbation Method）、Cotter方法等。

（3）全局方法：多為方差分解方法，根據單個輸入變量或其組合的貢獻來分解模型輸出的方差。典型的方法有：Morris方法、Borgonovo指數方法、ANCOVA指數方法等。

本文提出基于LM神經網絡的敏感性分析方法，分析LM神經網絡算法與敏感性分析之間的理論關系，基于不確定量化分析工具UQLab[1]生成分析樣本并計算量化的敏感性分析結果，通過對結果的對比分析，驗證方法分析的可靠性并進一步討論樣本數量對計算結果的影響。

一、LM神經網絡算法與敏感性分析

為了說明LM神經網絡算法與敏感性分析的關系，首先考慮一個多元函數：

其中，L是感興趣輸出，xi是輸入參數。

令輸入參數的變化量分別為 Δx1,Δx2,...,Δxi,Δxn，感興趣輸出的變化量為 ΔL。根據多元函數的泰勒展開式可得：

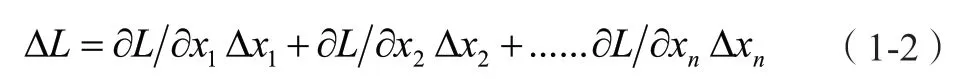
定義L對xi的敏感度Si為L的變化率與參數xi變化率之比。Si的數值可以通過下式計算：

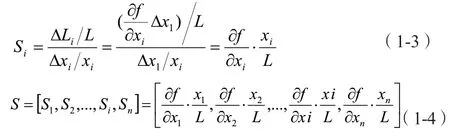
其中，xi與L值均為已知參數，因此，敏感性量化分析的核心是求解多元函數f(x1,x2,...,xi,xn)關于輸入參數的一階偏導即Jacobian矩陣。

LM神經網絡算法是被設計為接近二階訓練速度而不必計算Hessian矩陣的算法。當神經網絡性能函數具有平方和的形式時（在訓練反向傳播網絡中是典型的），Hessian矩陣可以近似為

并且梯度可以計算為

其中J即是Jacobian矩陣，包含關于權重和偏差的網絡誤差的一階導數，e是網絡誤差的矢量。

LM神經網絡算法以類似Gauss-Newton算法對Hessian矩陣進行近似

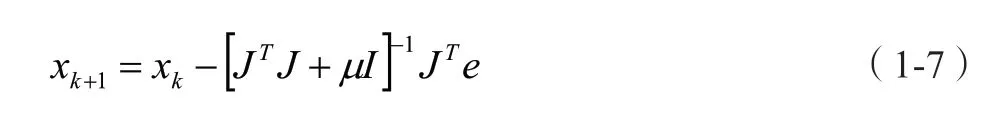
同時通過標準反向傳播技術并在最后一層附以一個修改來計算Jacobian矩陣

上式中矩陣的每列是靈敏度矢量，通過網絡反向傳播產生一行Jacobian行列式。

根據LM神經網絡算法的特點，訓練神經網絡得到的權值即能反映模型的敏感性。由此提出了基于LM神經網絡算法的敏感性分析方法，以下采用不確定性量化分析工具得到的樣本及已有的敏感性分析結果對方法進行驗證。

二、基于LM神經網絡算法的敏感性分析方法驗證

1.敏感性分析結果

本文以堆芯子通道模型作為驗證計算實例，選擇通道冷卻劑入口溫度、線功率、系統壓力、格架位置、平均入口質量流速作為不確定性源，其概率密度分布函數見表1，其中，X1表示平均值，X2表示標準差，標準差大小均為平均值的1%。基于不確定性量化分析工具生成3000個樣本，并應用輸入/輸出相關性（Input/output correlation）、標準回歸系數（Standard Regression Coefficients）、Morris等敏感性分析方法，得到結果如表2所示。

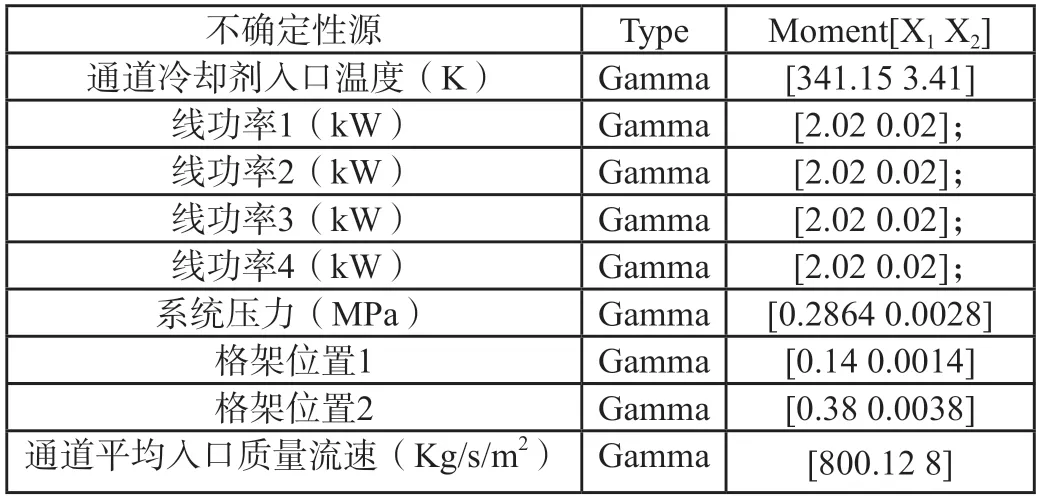
表1 不確定性源概率密度函數分布

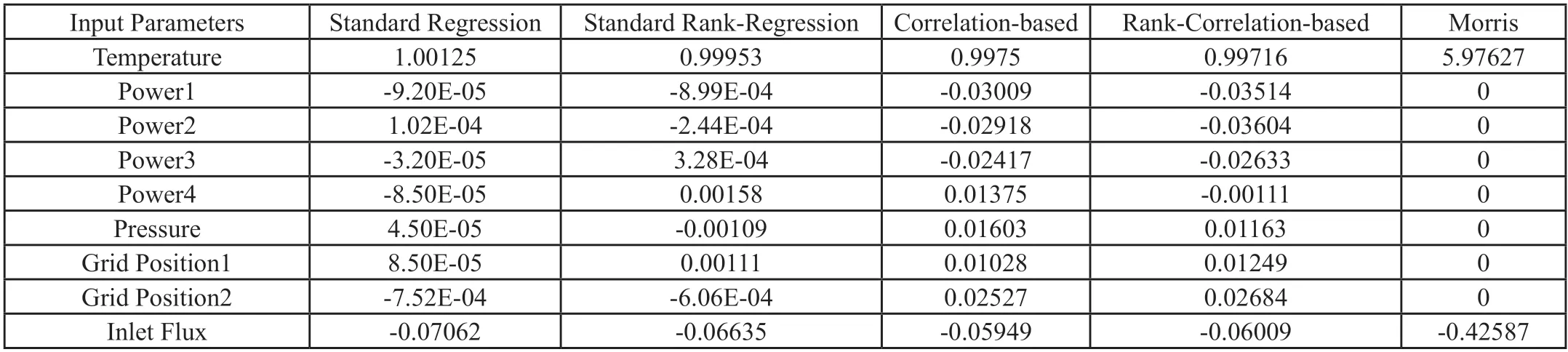
表2 敏感性分析結果表

2.基于LM神經網絡算法的敏感性分析

基于得到的3000個樣本，使用2層LM神經網絡進行訓練，如圖1所示。以隱藏層包含10個神經元節點的LM神經網絡為例，在神經網絡訓練完成后，得到表征輸入到隱藏層即Jacobian矩陣的權重iw和修正Jacobian矩陣的最后一層的權重lw，如表3、表4所示。如上所述，表4矩陣的每列權重表征的是靈敏度矢量，用以修正表3相對應的行權重值。用表4作為行矩陣乘以表3，即可得到最終的敏感性結果，即

表4 修正Jacobian矩陣的權重lw

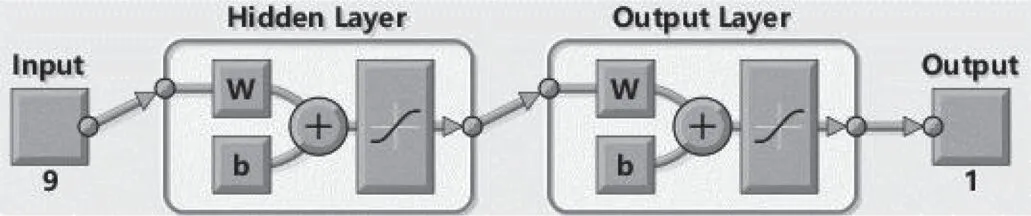
圖1 神經網絡圖

具體值如表5第10行所示。使用同樣的方法得到不同神經元節點時的敏感性分析結果，得到表5。

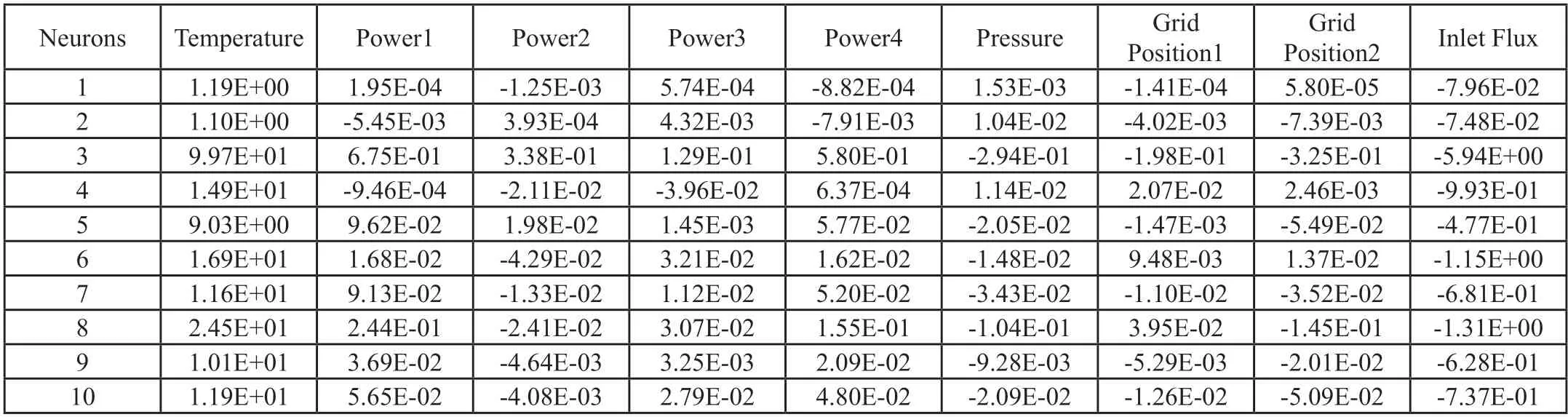
表5 不同數量神經元節點時的敏感性分析結果

考慮到不同方法得到的線功率、系統壓力、格架位置的敏感性指數的值均極小，只對比不同方法得到的通道冷卻劑入口溫度、平均入口質量流速敏感性指數相對值。得到堆芯子通道計算模型敏感性相對指數圖，如圖2所示。

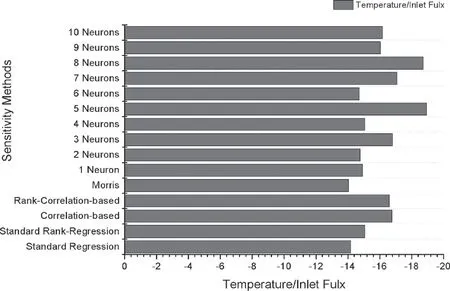
圖2 堆芯子通道計算模型敏感性相對指數

在圖2中，各方法得到的關于通道冷卻劑入口溫度、平均入口質量流速敏感性指數相對值相近，相關性結果相同，增加或減少隱藏層的神經元節點并沒有顯著的改變敏感性分析結果，基于LM神經網絡的敏感性分析方法是有效的。

3.訓練樣本數對LM神經網絡算法敏感性分析結果的影響

為了進一步討論訓練樣本數對分析結果的影響，以10為步長，以10個樣本數為起點，依次從3000個樣本中隨機選擇對應數量的樣本，以此作為神經網絡新的樣本。再使用不同數量神經元節點的2層LM神經網絡訓練樣本，得到分析結果。同樣只對比通道冷卻劑入口溫度、平均入口質量流速敏感性指數相對值，如表6所示。

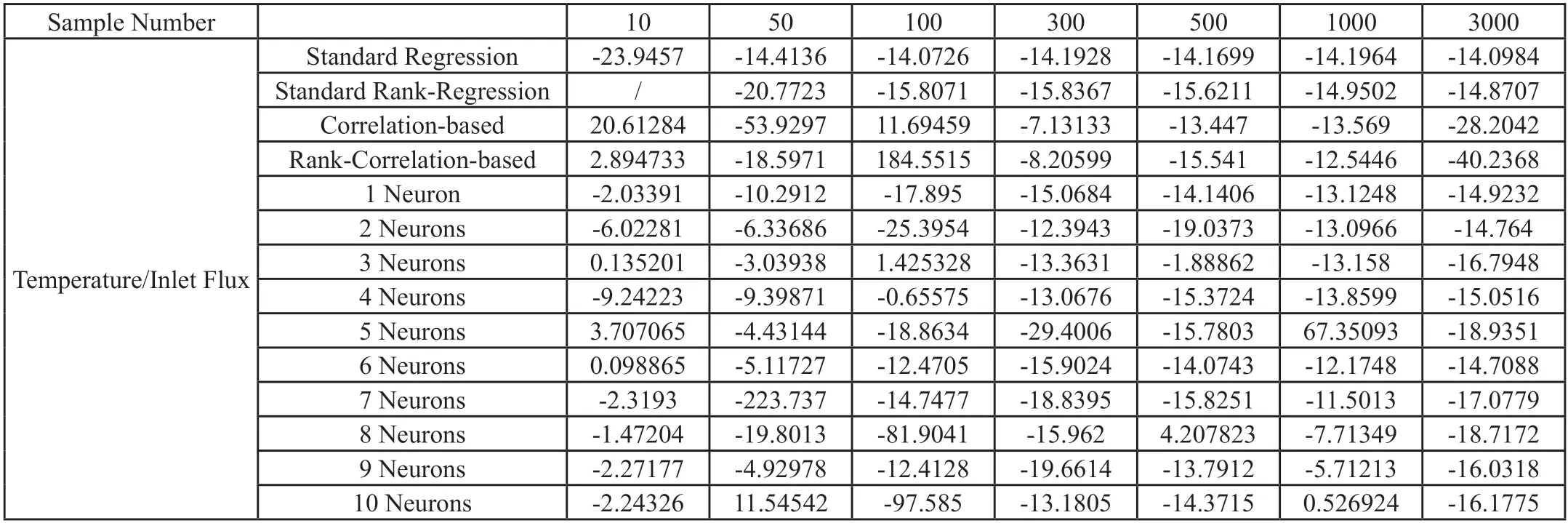
表6 不同樣本數敏感性相對指數結果

在表6中，只使用一個神經元節點時，計算結果隨樣本數收斂速度極快，在樣本數量達到20以后，敏感性分析結果就已趨于穩定值，穩定性極好。增加神經元節點后，計算結果的收斂性和穩定性變差。

結語

基于LM神經網絡算法的敏感性分析方法是可用的，并具有準確性好、收斂快的特點。當使用隱藏層只包含1個神經元節點的2層LM神經網絡時，敏感性分析結果隨訓練樣本數收斂速度最快、穩定性最好。