間歇過程的批內(nèi)自優(yōu)化控制

葉凌箭

化工過程普遍存在不確定性,如何采用有效的優(yōu)化方法找到不確定條件下系統(tǒng)的真實最優(yōu)點,對提高化工企業(yè)的經(jīng)濟(jì)效益發(fā)揮著關(guān)鍵作用[1].大規(guī)模化工過程的控制系統(tǒng)通常為分層遞階結(jié)構(gòu)[2-3],控制層(下層)的主要任務(wù)是抑制底層擾動,跟蹤優(yōu)化層傳遞來的被控變量設(shè)定值,優(yōu)化層(上層)根據(jù)調(diào)度層(頂層)傳達(dá)的生產(chǎn)任務(wù)指標(biāo)等,對當(dāng)前工況進(jìn)行識別,執(zhí)行相應(yīng)的優(yōu)化算法計算出最優(yōu)設(shè)定值,傳遞給控制層執(zhí)行.

優(yōu)化層執(zhí)行的優(yōu)化算法通常以化工過程的非線性模型為基礎(chǔ),以傳統(tǒng)的“二步法” 實時優(yōu)化[4-5]為例,首先確定模型的不確定參數(shù),運行過程中采集系統(tǒng)的輸出量數(shù)據(jù),對未知參數(shù)進(jìn)行估計,再基于更新的系統(tǒng)模型進(jìn)行重優(yōu)化,計算出被控變量的最優(yōu)設(shè)定值后傳遞給控制層.這一過程通常還需要結(jié)合數(shù)據(jù)調(diào)和、穩(wěn)態(tài)檢測等技術(shù)手段加強(qiáng)優(yōu)化結(jié)果的可靠性,工業(yè)過程的優(yōu)化周期一般為4～8 小時.針對傳統(tǒng)的“二步法”的缺點,近年來涌現(xiàn)出了新的實時優(yōu)化方法,如Bonvin 課題組提出的修正項自適應(yīng)方法(Modifier adaptation)[6-7],通過對標(biāo)稱模型的約束及梯度進(jìn)行修正,即使不估計擾動參數(shù)也能收斂到真實最優(yōu)點.文獻(xiàn)[8-10]考慮運行層之間的不同時間尺度,提出了數(shù)據(jù)驅(qū)動的多速率分層運行優(yōu)化控制方法,基于Q 學(xué)習(xí)對基礎(chǔ)控制回路的設(shè)定值進(jìn)行在線優(yōu)化,使運行層能更好地優(yōu)化控制性能指標(biāo).自優(yōu)化控制(Self-optimizing control,SOC)[11-13]提出通過離線選擇控制層的被控變量,設(shè)定值則在線保持不變,提供了實時優(yōu)化的另一種研究思路.在自優(yōu)化控制中,被控變量可以是常規(guī)物理量的函數(shù),即構(gòu)造虛擬量進(jìn)行控制,可使系統(tǒng)的操作變量可以在不確定性下進(jìn)行自尋優(yōu).當(dāng)?shù)讓涌刂频膬?yōu)化作用較強(qiáng)時(經(jīng)濟(jì)損失可接受),甚至可以省略單獨的優(yōu)化層,從而簡化控制系統(tǒng).相比傳統(tǒng)的優(yōu)化方式,自優(yōu)化控制的優(yōu)化在工作頻率為秒/分的反饋控制中完成,因此優(yōu)化速度得到大幅度提升,在一系列研究中表現(xiàn)出良好的效果[14-17].

間歇過程是一類批次加工的化工過程,具有規(guī)模小、靈活性高的特點,在需求多元化的現(xiàn)代市場中應(yīng)用越來越廣泛.相比連續(xù)化工過程,間歇過程具有“多重時變”的操作特征[18-19].一方面,間歇過程具有重復(fù)特性,可以引入學(xué)習(xí)機(jī)制從歷史批次的數(shù)據(jù)中提煉出有用的信息,改進(jìn)后續(xù)批次的跟蹤控制和經(jīng)濟(jì)指標(biāo)優(yōu)化,典型的如迭代學(xué)習(xí)控制[18,20-23]、批間實時優(yōu)化[23-24]等控制和優(yōu)化技術(shù).另一方面,由于其時變特性,間歇過程在批次內(nèi)無穩(wěn)定操作點,相比連續(xù)過程的控制和穩(wěn)態(tài)優(yōu)化更具挑戰(zhàn)[25-27].自優(yōu)化控制經(jīng)過近20 年的發(fā)展,針對連續(xù)過程已報道了一系列被控變量求解方法[12,28-31],但是針對需動態(tài)優(yōu)化的間歇過程仍缺乏足夠的研究.值得注意的是,由于從批間角度看間歇過程是一個靜態(tài)過程[32],近年來文獻(xiàn)[33-34]提出了間歇過程的批間自優(yōu)化控制方法.此類方法僅利用了間歇過程的重復(fù)性,基于已有的靜態(tài)自優(yōu)化控制方法求解被控變量,然后設(shè)計批間控制器調(diào)節(jié)輸入軌跡,逐批次將被控變量控制于恒定設(shè)定點,實現(xiàn)實時優(yōu)化.但批間優(yōu)化本質(zhì)上還是靜態(tài)方法,由于需要若干個批次才能實現(xiàn)被控變量的跟蹤控制,優(yōu)化作用慢,因此未充分發(fā)揮自優(yōu)化控制的優(yōu)勢.此外,批間優(yōu)化只對具有重復(fù)特性的擾動具有效果,當(dāng)系統(tǒng)受到高頻擾動作用時,批間控制器難以實現(xiàn)有效的實時優(yōu)化.

最近,Ye等[35]提出了一種針對間歇過程的動態(tài)自優(yōu)化控制方法,通過考慮批內(nèi)變量的因果性,最終得到了具有優(yōu)化作用的控制律.設(shè)計控制系統(tǒng)時,選擇被控變量和設(shè)計控制器通常是兩個獨立任務(wù)[36],前者主要考慮經(jīng)濟(jì)指標(biāo)的優(yōu)化,后者關(guān)注于如何更好地跟蹤控制被控變量,保證控制系統(tǒng)的穩(wěn)定性和魯棒性.如何在此前提下求解批內(nèi)被控變量,仍是一個開放的課題.

本文研究了間歇過程的批內(nèi)自優(yōu)化控制問題,貢獻(xiàn)如下:1)基于自優(yōu)化控制策略提出以輸出變量的線性組合為被控變量(虛擬變量),在批次運行過程中對其進(jìn)行跟蹤控制,以控制手段實現(xiàn)實時優(yōu)化;2)根據(jù)是否在過程不同階段切換被控變量,給出了兩種自優(yōu)化控制策略,對每種策略又分別給出了兩種設(shè)定軌線選取方案;3)引入擴(kuò)張組合矩陣,將這些情形統(tǒng)一描述為具有不同結(jié)構(gòu)約束的最優(yōu)組合矩陣求解問題,并推導(dǎo)得到了其中一種方案的解析解計算方法.目前為止,本文所提方法在國內(nèi)外文獻(xiàn)中未見報道.

1 連續(xù)過程的自優(yōu)化控制

對連續(xù)化工過程,考慮如下靜態(tài)優(yōu)化問題

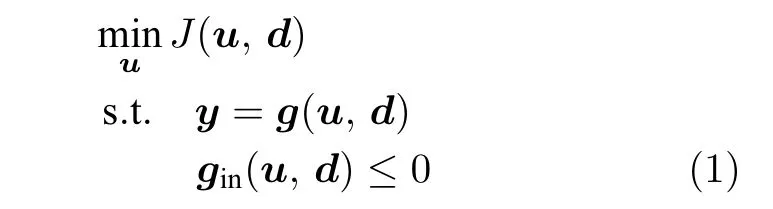
其中,J為經(jīng)濟(jì)指標(biāo),分別是操縱變量、擾動變量和測量變量,g和gin為輸出變量的模型函數(shù)和約束條件.

擾動變量d變化且在線不可測是化工過程偏離最優(yōu)點的主要原因.當(dāng)擾動變量d變化時,式(1)的解是d的函數(shù),不妨記為uopt(d).實時優(yōu)化的任務(wù)是在d未知的前提下,尋找到新的最優(yōu)值uopt,實現(xiàn)過程的最優(yōu)操作.自優(yōu)化控制(SOC)通過構(gòu)造虛擬的被控變量c=Hy,當(dāng)反饋控制器將c控制在恒定設(shè)定值cs上時,控制器輸出能自動逼近當(dāng)前的實際最優(yōu)值uopt(d). 當(dāng)組合矩陣H每行有且只有一個1,其余為0 時,c為輸出變量y的子集,此時退化為傳統(tǒng)的以單變量為被控變量的情形.更一般的情況下,H中的非零元素提供了更多優(yōu)化自由度,可提高系統(tǒng)的閉環(huán)經(jīng)濟(jì)性能.例如,假設(shè)系統(tǒng)自由度nu=2,y=[T P cA]T,包括溫度T,壓力P和物質(zhì)A的濃度cA,考慮兩種情況:

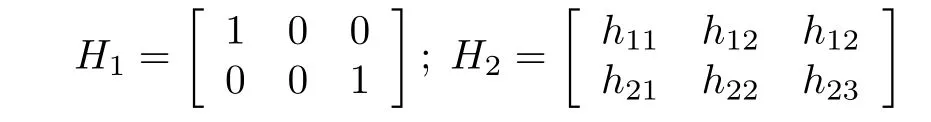
H1對應(yīng)的被控變量c=H1y為T和cA(單個物理量),H2的被控變量為3 個物理量的線性組合.顯然,前者為后者的一種特殊形式.

為求解一般情形的最優(yōu)組合矩陣H,研究人員針對不同過程特性和衡量標(biāo)準(zhǔn)提出了求解方法[12,28-31].以一種針對線性系統(tǒng)的局部法(Exact local method)為例[28],首先定義損失函數(shù)L

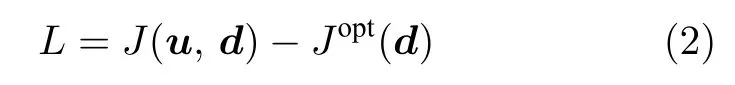
對給定的d,將J(u,d)在最優(yōu)點uopt處進(jìn)行二階泰勒展開

引理1[35].Lav(H)=Lav(QH),其中Q為任意nu維非奇異方陣.

引理1 表明,式(9)的解非唯一(因為控制c=Hy和c=QHy等效).利用該特性,可以先求解出式(9)的一個特解,再推廣至通解形式.文獻(xiàn)[24]給出了最優(yōu)H的一個特解,即

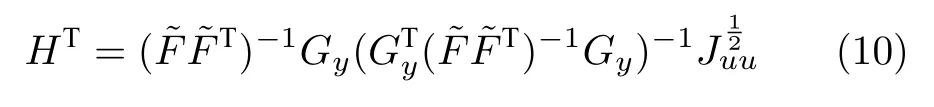
2 間歇過程的自優(yōu)化控制

2.1 間歇過程優(yōu)化

考慮一類帶不確定參數(shù)的間歇過程優(yōu)化問題

對式(11)所示的動態(tài)優(yōu)化問題,通常可以基于數(shù)值法將其近似為離散化的非線性規(guī)劃(Non-linear programming,NLP)問題[37]

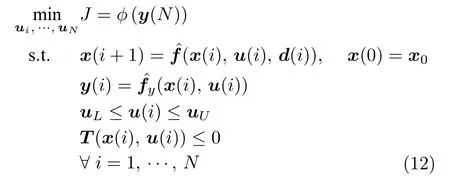
式中,N為間歇過程在操作區(qū)間[ 0,tf] 內(nèi)的離散段數(shù),代表離散后的非線性狀態(tài)方程和輸出方程.

對上述間歇過程的優(yōu)化問題,文獻(xiàn)[27-28]提出了批間自優(yōu)化控制方法,即構(gòu)造被控變量c=Hy,利用間歇過程的重復(fù)特性逐批次將c控制在恒設(shè)定值上.從批間角度看,間歇過程是一個靜態(tài)過程,因此第1 節(jié)中針對連續(xù)過程的被控變量求解方法可以較為直接地拓展至間歇過程.但批間優(yōu)化需要經(jīng)歷若干批次實現(xiàn)被控變量的控制,優(yōu)化速度較慢.并且,若擾動的變化頻率較高(如非重復(fù)性擾動),則難以實現(xiàn)被控變量的跟蹤控制,優(yōu)化效果有限.

2.2 批內(nèi)自優(yōu)化控制策略

本文研究間歇過程的批內(nèi)自優(yōu)化控制方法,即在單批次中控制被控變量實現(xiàn)實時優(yōu)化.與批間優(yōu)化相比,批內(nèi)優(yōu)化的響應(yīng)速度更快,能提高優(yōu)化效果.由于跟蹤控制在單批次內(nèi)完成,批內(nèi)優(yōu)化能應(yīng)對非重復(fù)性擾動.對被控變量c=Hy及其設(shè)定值cs,考慮如下幾種策略:

策略1.H和cs保持恒定;

策略2.H恒定,cs時變;

策略3.H和cs均時變.

策略1 為連續(xù)過程中采用的自優(yōu)化控制方法,對具有時變特性的間歇過程,一般難以取得理想效果.策略2 采用恒定被控變量,其設(shè)定值為動態(tài)軌線,較策略1 更適合間歇過程.策略3 進(jìn)一步考慮具有切換結(jié)構(gòu)的控制系統(tǒng),對離散化的間歇過程,在 [ti,ti+1)時間段內(nèi)控制一組新的被控變量,如圖1 所示.

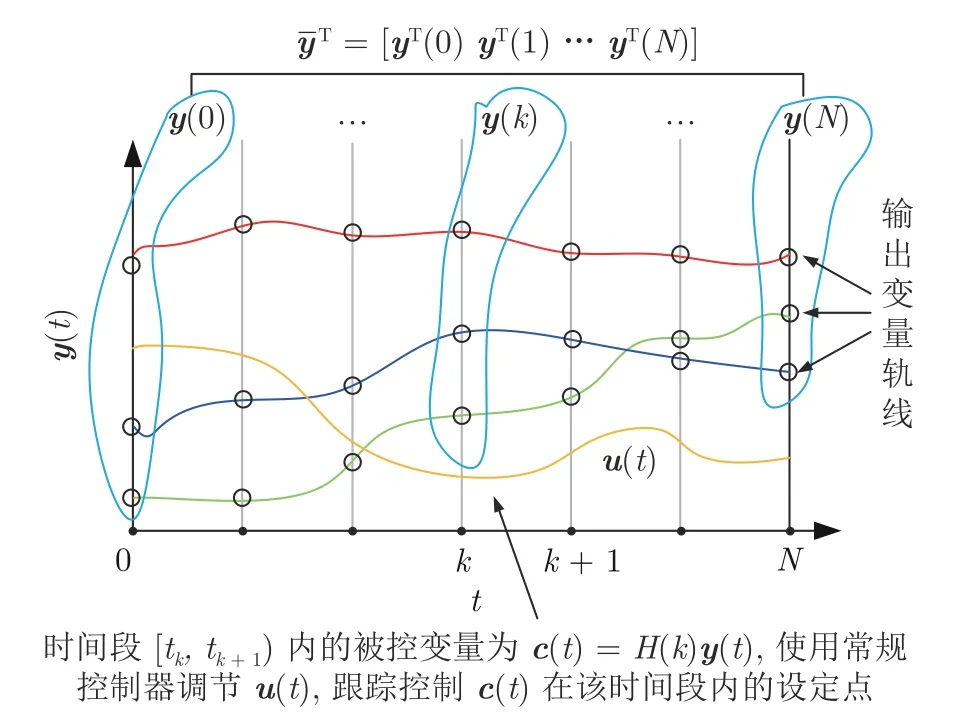
圖1 間歇過程的離散化變量及自優(yōu)化控制策略Fig.1 Discretization of batch processes and self-optimizing control strategy

結(jié)合間歇過程的時變特性,本文主要研究策略2 和策略3的被控變量求解問題.對此,引入如下假設(shè)條件:

可以看到,方案1 中被控變量的設(shè)定軌線固定不變.而方案2的被控變量設(shè)定軌線在當(dāng)前批次運行過程中不斷利用測量值進(jìn)行修正.相比方案1,方案2 更加充分地利用了過程信息,理論上能進(jìn)一步提高優(yōu)化效果,但需求解額外的決策變量H′(i),i=1,···,N.

為推導(dǎo)這兩種方案中損失函數(shù)與組合矩陣H之間的關(guān)系,定義如下超向量

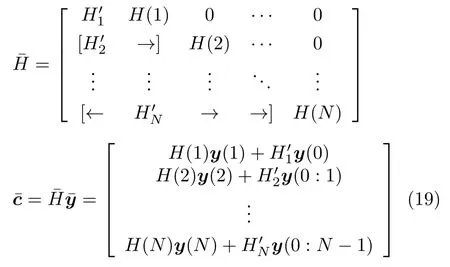
與策略2 相比,策略3 中兩種方案的組合矩陣H是時變的,即需求取N個組合矩陣H(i),i=1,···,N.同理,對策略3 求解如下最優(yōu)化問題

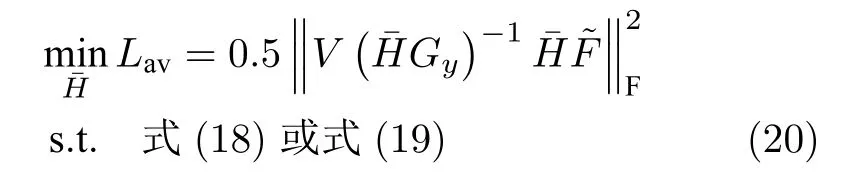
從以上分析看到,對不同的控制策略和設(shè)定值選取方案,可以統(tǒng)一歸結(jié)為具有不同結(jié)構(gòu)的擴(kuò)張組合矩陣的求解問題,可以在優(yōu)化問題中對施加等式約束實現(xiàn).一般來說,具有特定結(jié)構(gòu)的組合矩陣難以求得閉合解,需使用數(shù)值優(yōu)化算法.

注1.以上提出的4 種被控變量選擇方案,從控制角度看,執(zhí)行策略2 (方案1)最簡單,但優(yōu)化效果可能較差;策略3 (方案4)理論上的優(yōu)化效果最好,但被控變量需要不斷切換,并且設(shè)定軌線也要在線修正.針對具體過程,需結(jié)合過程特性和優(yōu)化性能結(jié)果綜合考慮這兩個因素,選擇最合理的自優(yōu)化控制方案.

2.3 策略3 (方案4)的解析解

下面提出一種針對策略3 (方案4)的閉合解求解方法.如式(19)所示,此時為塊下三角矩陣.為表述方便,將式(19)所示的表達(dá)式記為

通過合理利用轉(zhuǎn)化矩陣Q,定理1 將目標(biāo)函數(shù)及約束條件分解到每個離散時間節(jié)點,能夠沿時間軸依次求解出子矩陣(i). 對?i=1,···,N,求解如下優(yōu)化問題

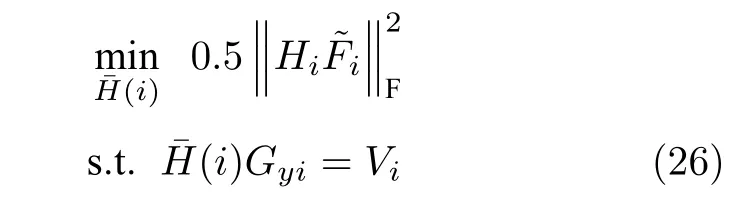
式(26)為帶等式約束的二次型凸優(yōu)化問題,可進(jìn)一步求得解析解.

定理 2.對式(26)所示的帶等式約束的二次型凸優(yōu)化問題,其閉合解為

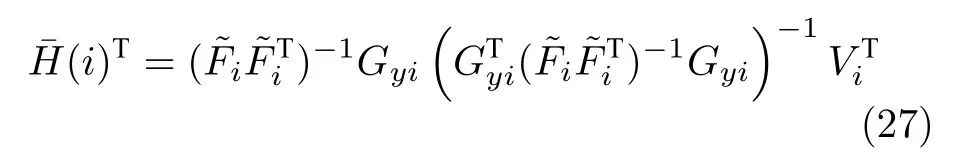
證明.式(26)在形式上與第1 節(jié)靜態(tài)自優(yōu)化控制問題一致,閉合解(27)的推導(dǎo)過程可參見文獻(xiàn)[28].□

綜上,本文求取最優(yōu)擴(kuò)張組合矩陣的計算步驟如圖2 所示,其中策略3 (方案4)可直接應(yīng)用定理2 求得閉合解,其他3 種情況則需使用數(shù)值優(yōu)化法求取.由于目標(biāo)函數(shù)Lav是的非線性函數(shù),優(yōu)化問題(17)和(20)不能保證得到全局最優(yōu)解.對此,策略3 (方案4)得到的解析解可作為數(shù)值優(yōu)化的初始解進(jìn)行尋優(yōu).

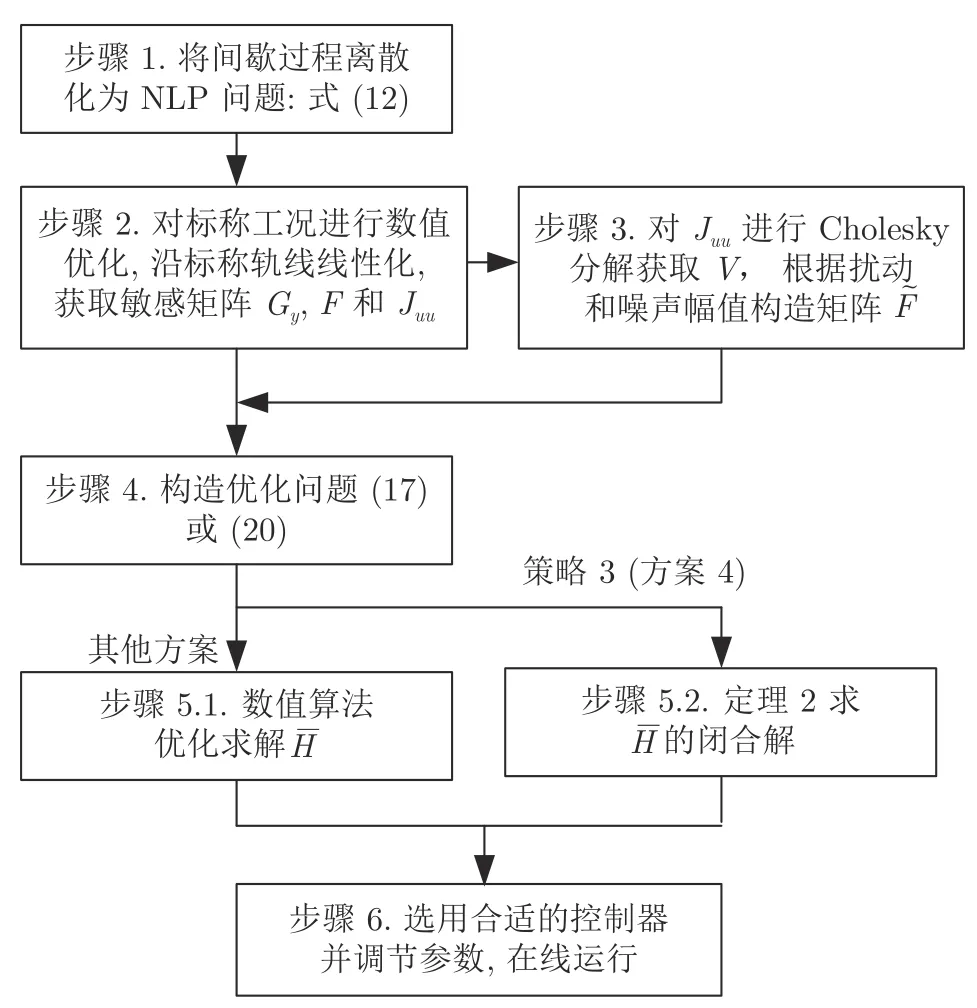
圖2 最優(yōu)擴(kuò)張組合矩陣 的求解步驟Fig.2 Procedure for solving the optimal extended combination matrix

3 仿真研究

3.1 間歇反應(yīng)器描述

本節(jié)研究一個帶副反應(yīng)的間歇反應(yīng)器,主副反應(yīng)分別為A+B →C和 2B →D,其中反應(yīng)物A在初始時刻投放完畢,B在反應(yīng)過程中實時投放,實時流量為操縱變量u(t).體系的模型方程為

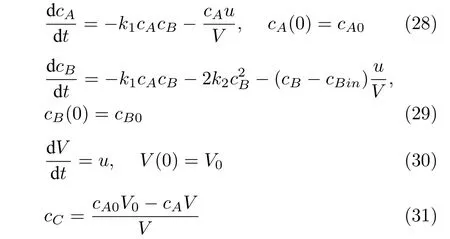
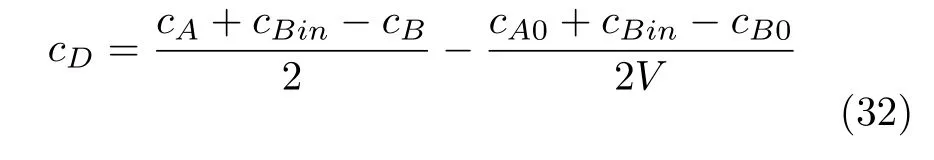
式中,cX表示物料X的濃度,V為持液量,其他符號含義及標(biāo)稱值列于表1.

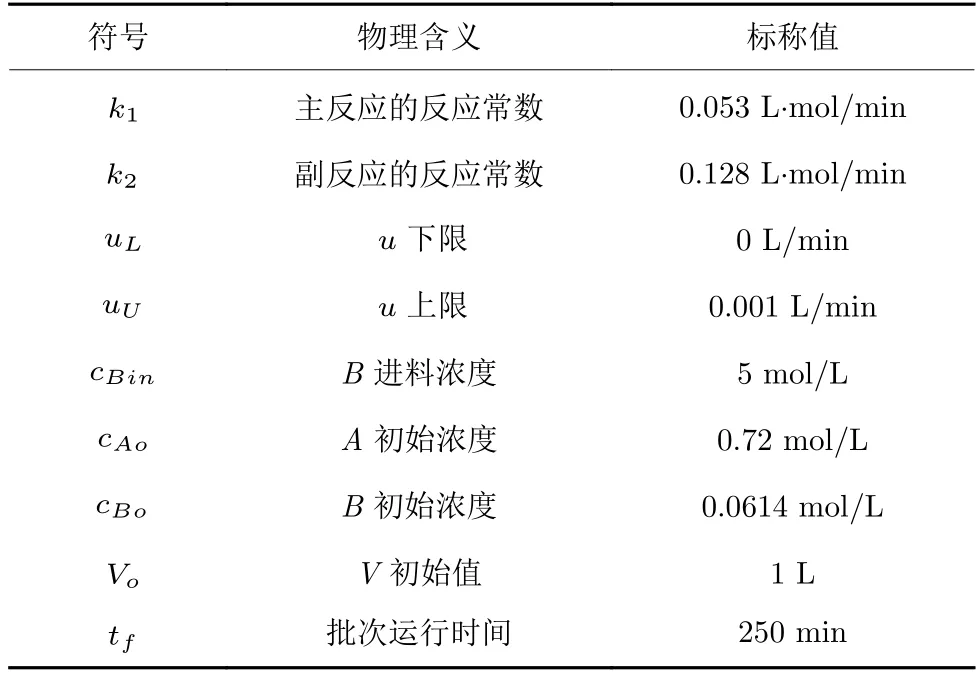
表1 間歇反應(yīng)器參數(shù)及標(biāo)稱值Table 1 Parameters for the reactor model and nominal values

操作目標(biāo)為在 [ 0,tf] 操作時段內(nèi)最大化產(chǎn)物產(chǎn)量C的同時減少副產(chǎn)物D,即表示為如下優(yōu)化問題

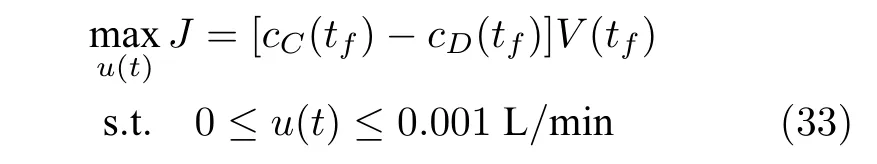
在表1 所示的標(biāo)稱工況下,使用數(shù)值優(yōu)化方法求解式(33)可得到u(t)的最優(yōu)輸入軌跡(圖3).可以看到,此時u(t)整個軌線處于可行域內(nèi),最優(yōu)值Jopt=0.271687 mol.反應(yīng)常數(shù)k1和k2為不確定擾動,變化范圍為其標(biāo)稱值的±40%.當(dāng)k1和k2變化時,u(t)的最優(yōu)輸入軌跡隨之改變.

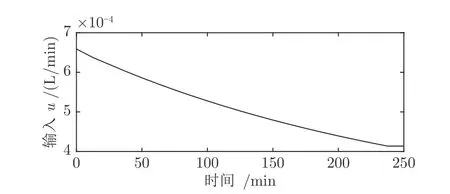
圖3 標(biāo)稱點的最優(yōu)輸入軌跡Fig.3 Optimal input trajectory at the nominal point

4 被控變量計算示例

為更清晰地闡述本文方法,以N=2 為例(即[0,tf]被均勻離散為兩段),介紹如何使用第2 節(jié)中的方法求解不同被控變量.離散后的優(yōu)化變量個數(shù)=2,對式(33)進(jìn)行重優(yōu)化后得到Hessian 矩陣和V矩陣

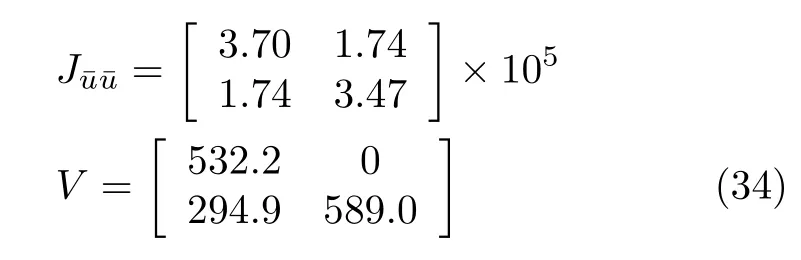
考慮使用cA和cB構(gòu)造被控變量,對離散系統(tǒng)進(jìn)行線性化,得到

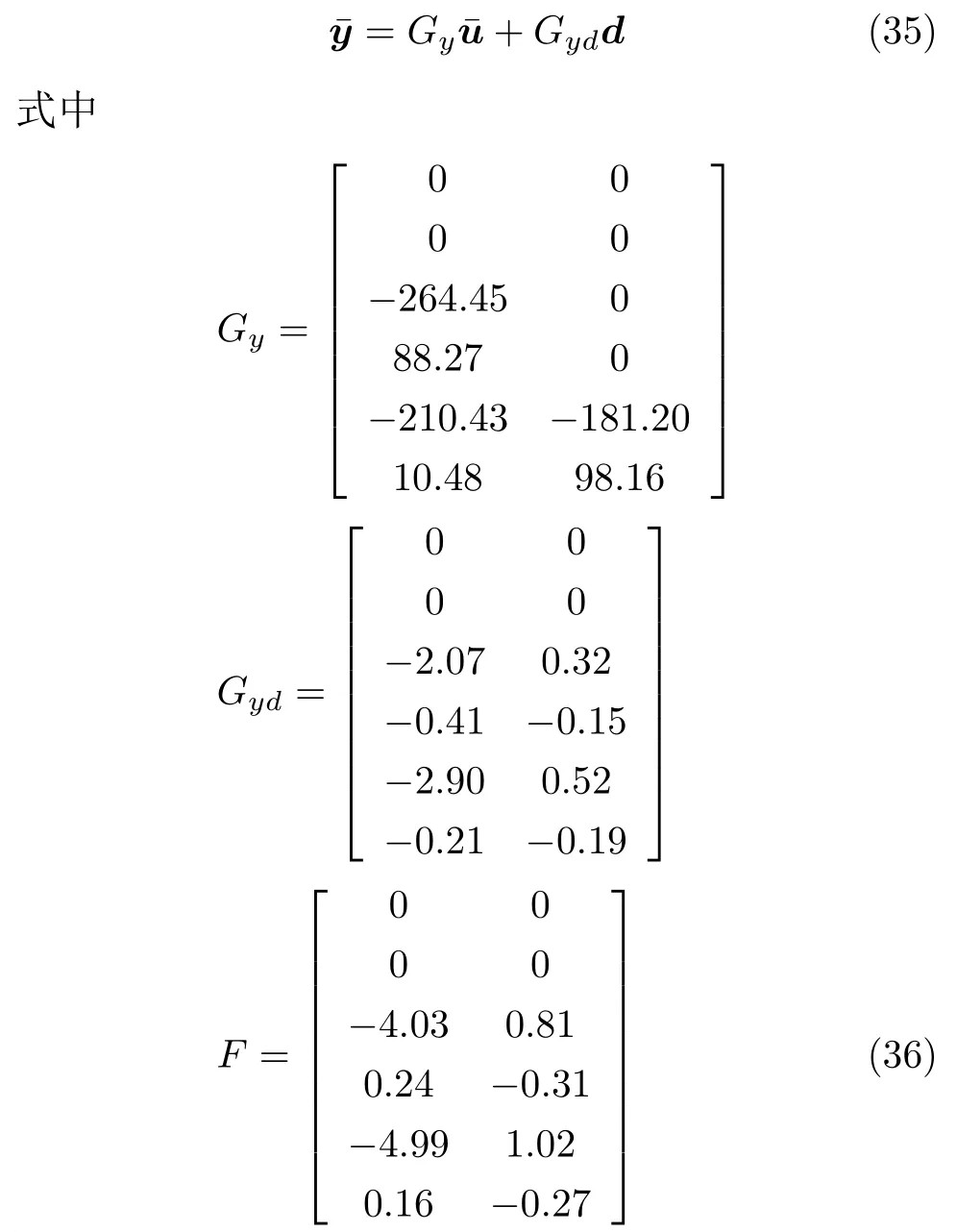
其中,測量變量=[yT(0)yT(1)yT(2)]為cA、cB分別在0,125 min 及250 min 時刻的量組成.得到上述矩陣后,可以構(gòu)造式(17)和式(20)所示的優(yōu)化問題來求解被控變量,結(jié)果如下.

1)策略2 (方案1):H=[-0.0026 0.0035],即整個時間段內(nèi)都控制被控變量c(t)=-0.0026cA+0.0035cB. 經(jīng)計算,前125 min的設(shè)定值為cs(1)=-0.000303,后125 min的設(shè)定值為cs(2)=-0.000059.

2)策略2 (方案2):求解得到的擴(kuò)張組合矩陣為

4.1 批內(nèi)自優(yōu)化控制效果

由于N=2 難以逼近整個間歇操作過程,后文設(shè)置N=20 并以相同的方法重新求解被控變量,同時,在測量變量中加入體積變量V提高優(yōu)化效果.從表2 可觀察到:

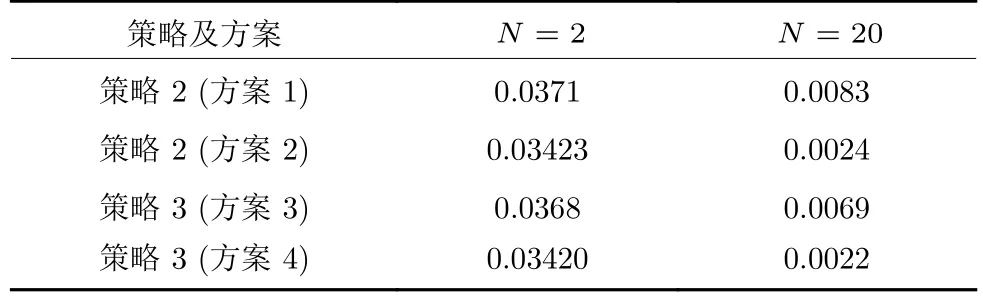
表2 損失函數(shù)LavTable 2 Loss functionLav

1)4 種方案的損失Lav在N=20 時,相比N=2都大幅度降低;

2)策略2 (方案1)的損失函數(shù)為0.0083,策略2 (方案2)通過在線設(shè)定值修正,進(jìn)一步將損失減少到0.0024;

3)策略3 (方案3)的損失為0.0069,略低于策略2 (方案1);

4)策略2 (方案3)的損失為 0.0024,與策略3(方案4)的損失0.0022 很接近,表明不切換被控變量也能得到較好的優(yōu)化控制效果.

基于表2的結(jié)果,策略2 (方案2)與策略3 (方案4)效果接近,但前者無需在線切換被控變量,更易于在線控制,因此考慮使用策略2 (方案2)對該反應(yīng)器進(jìn)行批內(nèi)自優(yōu)化控制.此外,動態(tài)仿真中將與策略2 (方案1)的結(jié)果進(jìn)行對比,有助于進(jìn)一步理解本文方法.

策略2 (方案1)的被控變量為c1(t)=0.0062cA+0.002cB+0.0831V,設(shè)定值軌線如圖4 所示.為進(jìn)一步獲取平滑的設(shè)定值軌線,使操作更為平穩(wěn),對這些離散點進(jìn)行回歸分析,得到平滑的設(shè)定值軌跡方程cs(t)=0.0877+3.705×10-5t-1.97×10-8t2,為一條隨時間t變化的連續(xù)曲線,如圖4 所示.對該系統(tǒng)可以采用普通的PI 控制器對被控變量c1(t)進(jìn)行跟蹤控制.

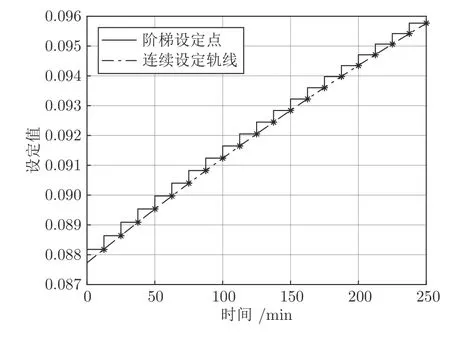
圖4 策略2 (方案1)的設(shè)定值軌線Fig.4 Setpoint trajectory for Strategy 2 (Scheme 1)

策略2 (方案2)的被控變量為c2(t)=0.0026cA+0.00032cB+0.0830V,設(shè)定值軌線在每批次運行過程中采集測量值進(jìn)行在線修正.為增強(qiáng)操作平穩(wěn)性,在tk時刻計算得到tk+1時刻的設(shè)定點后,在[tk,tk+1]時間段內(nèi)設(shè)置斜坡形設(shè)定值軌線,使設(shè)定軌線維持連續(xù)性.同樣使用PI 控制器跟蹤控制得到的被控變量c2(t).

不確定參數(shù)k1和k2分別改變 +20%和 -20%時的優(yōu)化控制效果如圖5 所示,從圖5(a)中可以看到,兩種方法分別對c1(t)和c2(t)都實現(xiàn)了較好的閉環(huán)跟蹤控制,其中,c2(t)的設(shè)定軌線根據(jù)批內(nèi)采集到的測量值進(jìn)行了調(diào)整,相比自身的標(biāo)稱軌線有一定程度的上移;圖5(b)顯示不同方法的控制輸入u(t)軌跡,其中,控制c1(t)時的u(t)軌跡相比標(biāo)稱操作更靠近當(dāng)前工況真實的最優(yōu)軌線,性能指標(biāo)J有所提高 (J=0.34374→0.34505),顯示出一定的優(yōu)化控制效果.控制c2(t)時的u(t)軌跡更靠近最優(yōu)軌線,其性能指標(biāo)J=0.34701和最優(yōu)值Jopt=0.34755差別不大.同時注意到控制c2(t)時的u(t)軌跡振蕩更加劇烈,這是因為c2(t)的設(shè)定軌線不斷在線修正,為了得到滿意的控制效果,使用了高增益PI 控制器 (Kp=20).這并不影響最終得到滿意的優(yōu)化效果 (L=0.00054),從另一個角度說明了間歇過程中控制關(guān)鍵變量的重要性.

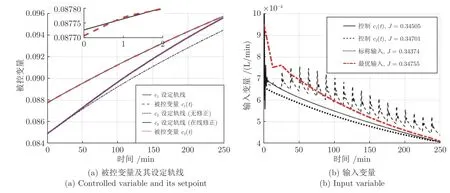
圖5 批內(nèi)自優(yōu)化控制效果 ( k1 :+20%,k2 :-20%)Fig.5 Within-batch self-optimizing performance ( k1 :+20%,k2 :-20%)

不確定參數(shù)k1和k2分別改變 -40%和 +40%時的優(yōu)化控制效果如圖6 所示,此時系統(tǒng)的不確定性向另一個方向變化,并且幅度更大.從圖6(a)中可以看到,兩種方法同樣對c1(t)和c2(t)都實現(xiàn)了較好的閉環(huán)跟蹤控制,其中,c1(t)的設(shè)定軌線不變,而c2(t)的設(shè)定軌線相比自身的標(biāo)稱軌線有一定程度的下移.從圖6(b)來看,雖然控制c1(t)能將u(t)軌跡向著真實的最優(yōu)軌線的方向調(diào)節(jié),其性能指標(biāo)J從標(biāo)稱操作的0.09646 提高到0.10312,但作用有限,距離最優(yōu)值Jopt=0.12252 仍有較大差距.控制c2(t)進(jìn)一步提高了優(yōu)化控制效果,其性能指標(biāo)為J=0.11602,相比最優(yōu)性能只有0.006的損失(此時k1,k2的變化較大,該損失在一定程度上由系統(tǒng)的非線性導(dǎo)致).此外,控制c2(t)時的u(t)軌跡同樣振蕩較為劇烈,但隨反應(yīng)進(jìn)行,u(t)大致圍繞著最優(yōu)軌線上下波動.

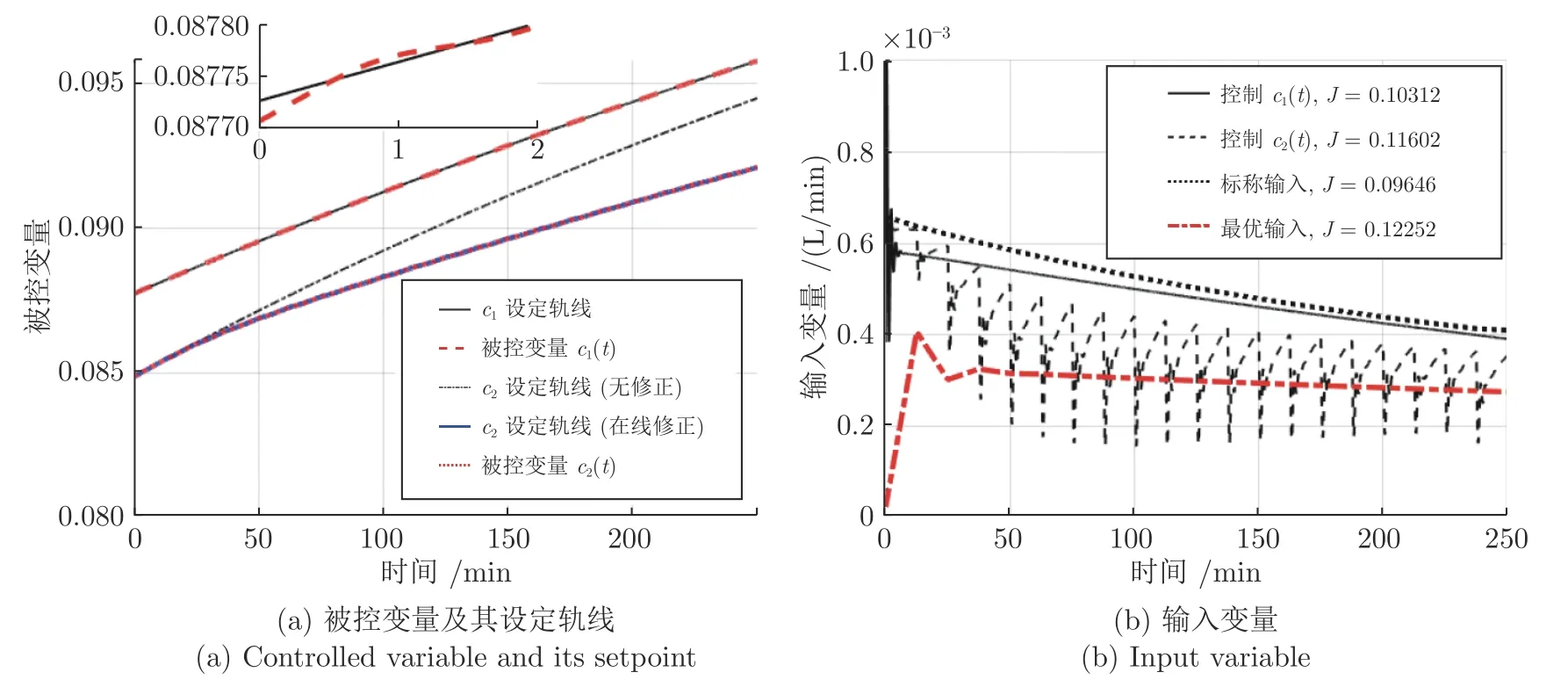
圖6 批內(nèi)自優(yōu)化控制效果 ( k1 :+40%,k2 :-40%)Fig.6 Within-batch self-optimizing performance ( k1 :+40%,k2 :-40%)

表3 進(jìn)一步統(tǒng)計了100 組隨機(jī)擾動下各方法的非線性損失,其中隨機(jī)擾動 [k1k2] 均勻分布在各自的變化范圍.可以看到,相比標(biāo)稱操作(平均損失0.0036)和以單變量cB(平均損失0.0042)為被控變量的情形,兩種批內(nèi)自優(yōu)化控制方法有效提高了經(jīng)濟(jì)性能,其中,策略2 (方案1)中控制c1(t)將平均損失減少到0.0026,策略2 (方案2)中控制c2(t)進(jìn)一步將平均損失減少到0.0007,幾乎可以忽略不計.此外,最大損失和標(biāo)準(zhǔn)差等統(tǒng)計量也呈現(xiàn)出相同的變化趨勢,如表3 所示.

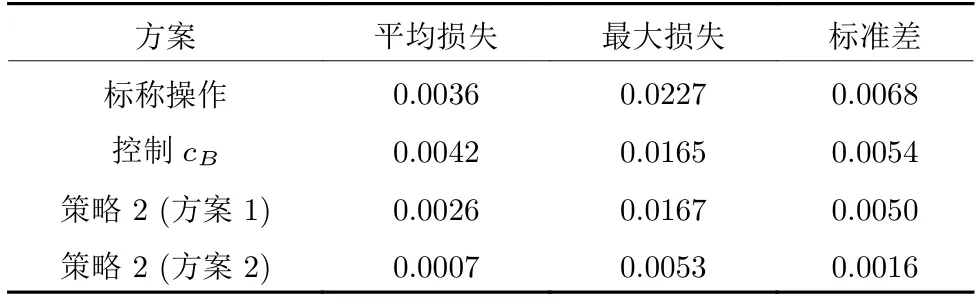
表3 100 組隨機(jī)擾動下的非線性損失統(tǒng)計量Table 3 Statistics of nonlinear losses for 100 groups of random disturbances

5 結(jié)束語

本文研究了間歇過程的批內(nèi)自優(yōu)化控制問題,在單批次運行過程中控制一組虛擬的被控變量(輸出變量的線性組合),實現(xiàn)間歇過程的實時優(yōu)化.對此,給出了兩種自優(yōu)化控制策略(被控變量恒定但設(shè)定值時變;被控變量和設(shè)定值均時變).對它們的設(shè)定值選取問題又分別提出兩種方案(設(shè)定值軌線固定不變;設(shè)定值軌線在線修正),共計4 種方法.通過引入擴(kuò)張組合矩陣,將這4種方法統(tǒng)一描述為具有不同結(jié)構(gòu)約束的最優(yōu)求解問題,并推導(dǎo)得到了策略3(方案4)的解析解計算方法(定理2).

本文提出的4 種被控變量選擇方法,其對應(yīng)的閉環(huán)控制系統(tǒng)具有不同的復(fù)雜度和優(yōu)化性能.針對一般的實際間歇過程,應(yīng)綜合考慮這兩個因素并取得合理權(quán)衡.間歇反應(yīng)器的仿真研究中,采用策略2(方案2)(恒定被控變量:c2(t))得到的控制結(jié)構(gòu)較為簡單,并且能通過在線修正c2(t)的設(shè)定值增強(qiáng)優(yōu)化效果,是較為合理的方案.