灰狼與郊狼混合優(yōu)化算法及其聚類優(yōu)化

張新明 姜云 劉尚旺 劉國奇 竇智 劉艷

在現(xiàn)實(shí)世界中,無時無處無不面臨著優(yōu)化問題.隨著社會的發(fā)展,急需處理的優(yōu)化問題越來越多樣化并越來越復(fù)雜.而諸如牛頓法、梯度下降法等傳統(tǒng)的方法不能夠很好地處理這些急需解決的優(yōu)化問題.因此,許多研究者建立了各種仿生類的智能計(jì)算模型,提出了許多智能優(yōu)化算法.群智能優(yōu)化算法(Swarm intelligence optimization algorithm,SIOA)是模擬自然界社會群體集體行為的一種智能優(yōu)化方法[1],包括粒子群優(yōu)化(Particle swarm optimization,PSO)算法[2]、灰狼優(yōu)化算法(Grey wolf optimizer,GWO)[3]、郊狼優(yōu)化算法(Coyote optimization algorithm,COA)[4]等.SIOA 具有易于實(shí)現(xiàn)、能有效處理全局優(yōu)化和大規(guī)模優(yōu)化問題等優(yōu)勢,廣泛應(yīng)用于多目標(biāo)優(yōu)化、數(shù)據(jù)聚類以及模式識別等諸多領(lǐng)域[5].但根據(jù)無免費(fèi)午餐定理[6],沒有任何一種SIOA 能獨(dú)立地解決所有的優(yōu)化問題,每種SIOA 都有自身的優(yōu)勢和局限性.因此許多學(xué)者提出了大量新奇和改進(jìn)的SIOA,其中包括算法的混合改進(jìn).兩種或多種算法的混合可以達(dá)到優(yōu)勢互補(bǔ),以獲得最佳的優(yōu)化性能[7].

GWO 是由Mirjalili等[3]于2014 年提出的一種新穎的SIOA,具有原理簡單、開采能力強(qiáng)、可調(diào)參數(shù)少等優(yōu)點(diǎn),但存在易陷入局部最優(yōu)、解決復(fù)雜優(yōu)化問題性能差等缺點(diǎn).因此許多學(xué)者對其進(jìn)行了研究和改進(jìn),其中包括混合改進(jìn).例如張新明等[7]提出一種GWO 與人工蜂群算法的混合算法,其中在人工蜂群觀察蜂階段自適應(yīng)融合GWO,以便增強(qiáng)開采能力和提高優(yōu)化效率.Zhang等[8]提出一種基于生物地理學(xué)優(yōu)化算法和GWO的混合算法,將改進(jìn)的基于生物地理學(xué)優(yōu)化算法和基于反向?qū)W習(xí)的GWO 混合,使得優(yōu)化性能最大化.Teng等[9]提出一種PSO 與GWO 結(jié)合的混合算法,該算法具有更好的尋優(yōu)能力和更強(qiáng)的魯棒性.Arora等[10]提出一種烏鴉搜索算法與GWO的混合算法,更有效地實(shí)現(xiàn)了全局優(yōu)化.

COA 是由Pierezan等[4]于2018 年提出的一種模擬郊狼群居生活、成長、生死等現(xiàn)象的新型SIOA.COA 具有獨(dú)特的搜索模型和結(jié)構(gòu)以及出色的優(yōu)化能力,尤其在解決復(fù)雜優(yōu)化問題優(yōu)勢明顯,但仍存在搜索效率低、可操作性不強(qiáng)以及收斂速度慢等缺陷,且由于COA 提出的時間較短,需改進(jìn)和完善并拓展其應(yīng)用領(lǐng)域.鑒于GWO 和COA 各有優(yōu)勢和不足,本文將兩種算法分別進(jìn)行改進(jìn)和簡化,得到改進(jìn)的COA (Improved COA,ICOA)和簡化的GWO (Simplified GWO,SGWO),然后通過正弦交叉策略將ICOA 和SGWO 有機(jī)融合在一起,從而獲得了一種性能優(yōu)越且高效的混合COA (Hybrid COA with GWO,HCOAG).另外,混合算法的研究一直是優(yōu)化領(lǐng)域的熱點(diǎn),因此研究GWO 與COA的混合是一項(xiàng)較有意義的工作.

1 灰狼優(yōu)化算法

GWO 模擬了自然界中灰狼種群嚴(yán)格的社會等級制度和群體捕食行為.在其社會等級制度中,灰狼從高到低依次為α,β,δ,ω狼.其捕食行為是追蹤和接近獵物、追捕和包圍獵物、攻擊和捕殺獵物.GWO 將狼群中的α,β,δ,ω狼的位置分別代表第一最優(yōu)解、第二最優(yōu)解、第三最優(yōu)解和候選解.灰狼包圍行為的數(shù)學(xué)模型為

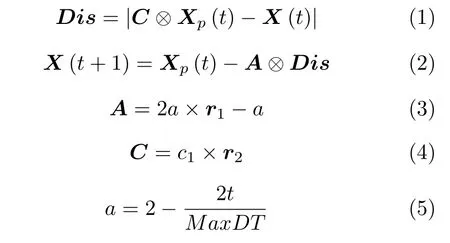
其中,Dis是灰狼與獵物間的距離,t是當(dāng)前迭代次數(shù),Xp是獵物的位置向量,X是灰狼的位置向量.A和C是系數(shù)向量.系數(shù)a在迭代過程中從2線性遞減到0,MaxDT是最大迭代次數(shù),r1和r2是[0,1]中的均勻分布隨機(jī)向量,c1為可調(diào)參數(shù)[11],?表示兩個向量各個對應(yīng)的分量相乘.狩獵行為的數(shù)學(xué)模型為

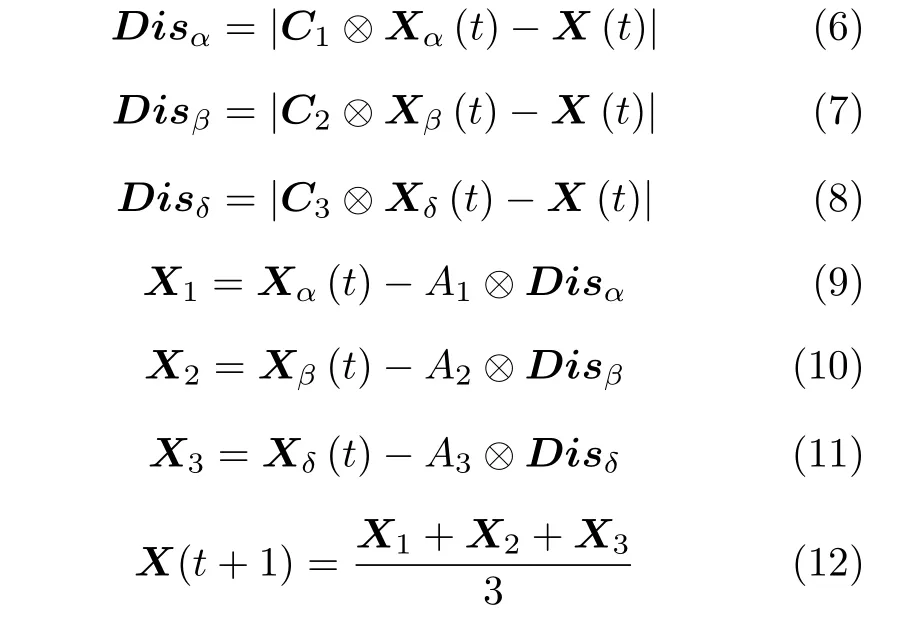
其中,Disα,Disβ和Disδ分別表示當(dāng)前狼與3 頭最優(yōu)灰狼間的距離.式(12)代表ω狼在α,β和δ狼的引導(dǎo)下移動的新位置,即GWO 產(chǎn)生的新解.GWO的流程圖見圖1.

從上述描述和圖1 可知,與PSO 等經(jīng)典的SIOA 相比,GWO的主要特點(diǎn)有:1)GWO 采用3 頭最優(yōu)狼(最優(yōu)解)引導(dǎo)ω狼圍獵,有較強(qiáng)的局部搜索能力,但在解決復(fù)雜優(yōu)化問題時,容易陷入局部最優(yōu);2)GWO 僅有兩個參數(shù)a和c1,前者采用動態(tài)調(diào)整方式,后者c1常取常數(shù)2,調(diào)整的參數(shù)少,故可操作性強(qiáng);3)原理簡單、易于實(shí)現(xiàn),但更新是基于維的計(jì)算,需計(jì)算式(6)～(12),故計(jì)算復(fù)雜度較高;4)目標(biāo)函數(shù)采用并行計(jì)算方式,故運(yùn)行速度較快.

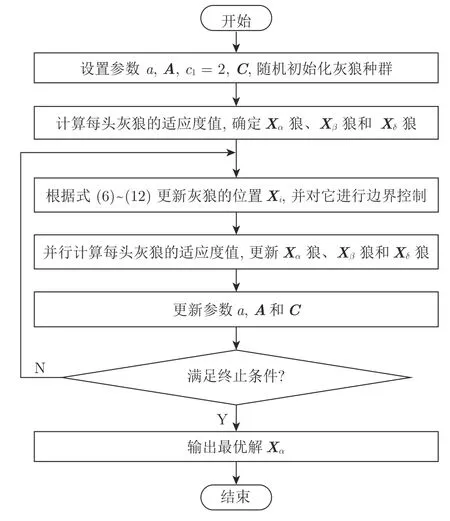
圖1 GWO的流程圖Fig.1 Flow chart of GWO

2 郊狼優(yōu)化算法

COA 包含初始化參數(shù)和狼群、組內(nèi)郊狼成長、郊狼生與死和被組驅(qū)離與接納[4]等4 個主要步驟.

2.1 參數(shù)初始化和隨機(jī)初始化郊狼群組

首先設(shè)置參數(shù),如郊狼群規(guī)模N,郊狼組數(shù)Np,組內(nèi)郊狼數(shù)Nc和MaxDT等,其中,N=Nc×Np.然后隨機(jī)初始化郊狼群組,第p組第c個郊狼第j維的隨機(jī)化操作如式(13).最后計(jì)算每頭郊狼soc的社會適應(yīng)度值fit,如式(14).

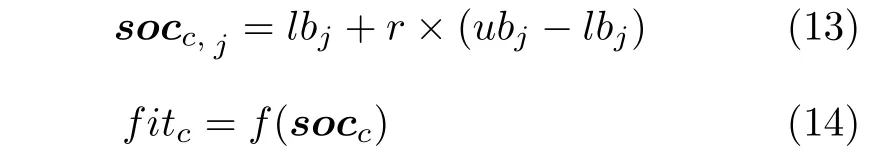
其中,lbj和ubj分別表示郊狼第j維社會狀態(tài)因子的下界和上界,j=1,2,···,D,D為搜索空間的維度,r為[0,1]內(nèi)均勻分布的隨機(jī)數(shù),f表示適應(yīng)度函數(shù).

2.2 組內(nèi)郊狼成長

組內(nèi)最優(yōu)狼alpha、組文化趨勢cult以及隨機(jī)選取的兩頭郊狼cr1和cr2影響組內(nèi)郊狼的成長過程,即組內(nèi)郊狼成長受δ1和δ2的影響.其中cult的計(jì)算如式(15)所示,即其每一個因素是組內(nèi)所有郊狼對應(yīng)社會因子的中位數(shù)(O為排名后的社會因子序列),故cult又稱中值郊狼.δ1和δ2計(jì)算見式(16)和式(17),郊狼的成長方式見式(18).

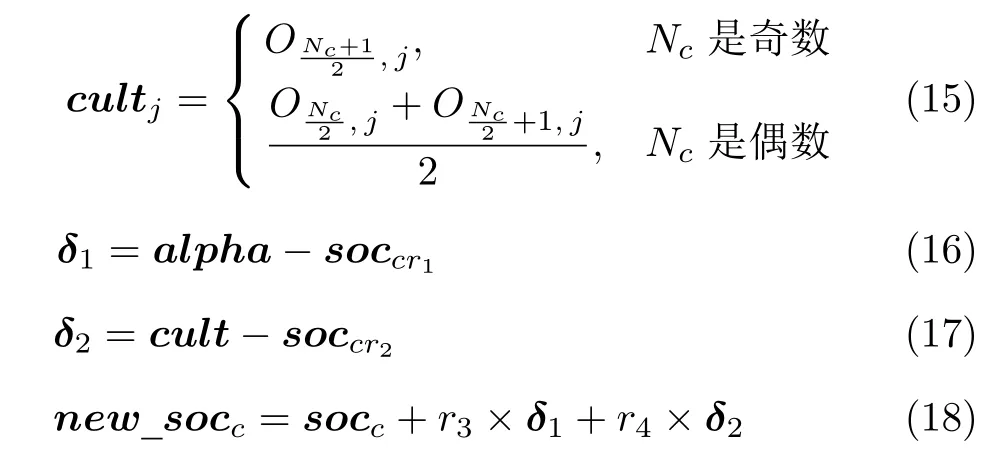
其中,new_socc是組內(nèi)第c頭郊狼成長獲得的新解,r3和r4是[0,1]內(nèi)均勻分布的隨機(jī)數(shù).組內(nèi)的郊狼成長后評估其社會適應(yīng)能力如式(19)所示,new_fitc為新適應(yīng)度值.

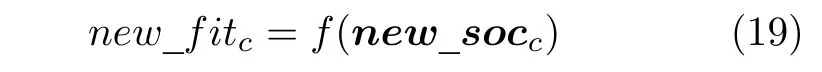
最后采用迭代貪心算法進(jìn)行優(yōu)勝劣汰(式(20)),如此新產(chǎn)生的更優(yōu)郊狼參與組內(nèi)其余郊狼成長以加快收斂速度.

2.3 郊狼生與死

幼郊狼 (pup)的誕生受隨機(jī)選擇父母郊狼的遺傳基因和環(huán)境因素的影響,見式(21)所示.

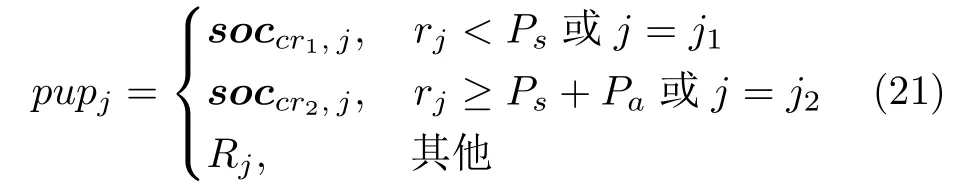
其中,rj是均勻分布在[0,1]內(nèi)的隨機(jī)數(shù);j1和j2是兩個隨機(jī)選擇的維度標(biāo)號,以確保兩個父郊狼的基因能夠遺傳給幼狼;Rj是在第j維決策變量范圍內(nèi)隨機(jī)產(chǎn)生的變異值;Ps和Pa分別是分散概率和關(guān)聯(lián)概率,它們決定著幼狼被遺傳和變異的情況,如式(22)和式(23)所示.

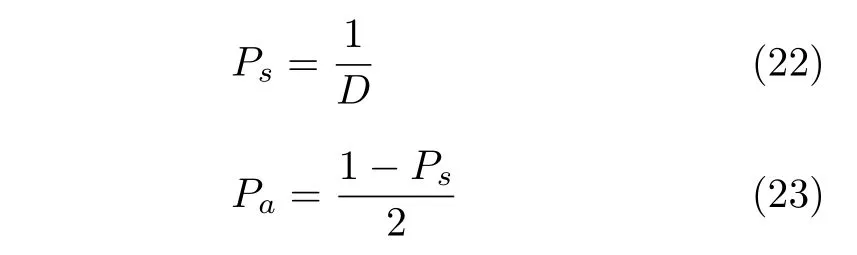
幼狼出生后,評估其社會適應(yīng)能力,并依照其能力決定生與死,具體描述如下:在社會適應(yīng)能力上,1)組內(nèi)只有一個郊狼比幼狼差時,則此郊狼死亡,幼狼存活,并設(shè)它的年齡為0,即age=0;2)組內(nèi)有多個郊狼比幼狼差時,能力差且年齡最大的郊狼死亡,幼狼存活,并設(shè)age=0;3)組內(nèi)所有郊狼都比幼狼強(qiáng)時,幼狼死亡.

2.4 郊狼被驅(qū)離和接納

在COA 中,郊狼以Pe的概率被組驅(qū)離和接納.郊狼初始被隨機(jī)分配到組群中,但有時某些郊狼會離開它所在組群而加入另一組群,這種隨機(jī)驅(qū)離和接納用來保證組內(nèi)郊狼的多樣性和組間信息共享,Pe的計(jì)算方式為

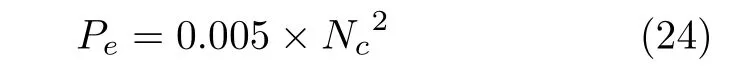
COA的偽代碼如算法1 所示.

算法1.COA 算法

從以上描述可知,與PSO 等經(jīng)典的SIOA 相比,COA的主要優(yōu)勢有:1)具有很好的搜索框架,即多組結(jié)構(gòu),郊狼隨機(jī)被組驅(qū)離和接納等使郊狼群具有多樣性,有較強(qiáng)的探索能力,能夠更好地解決復(fù)雜優(yōu)化問題[12];2)組內(nèi)最優(yōu)郊狼和組內(nèi)文化趨勢引導(dǎo)組內(nèi)每個郊狼的成長,增強(qiáng)了局部搜索能力;3)郊狼組內(nèi)的生與死受隨機(jī)選擇父郊狼的遺傳因子和環(huán)境變異因子影響,郊狼生與死算子使得COA具有一定的全局搜索能力.其主要不足有:1)結(jié)構(gòu)復(fù)雜,計(jì)算復(fù)雜度高;2)采用迭代貪心算法,穩(wěn)定性差,效率低;3)需調(diào)整的參數(shù)多,如Pe,Np和Nc等需調(diào)整,可操作性差;4)多組結(jié)構(gòu)等雖然增強(qiáng)了探索能力,但組與組之間信息共享不足,導(dǎo)致搜索后期收斂速度慢.

3 灰狼與郊狼混合優(yōu)化算法

3.1 提出HCOAG的動機(jī)

COA 與GWO 雖然同屬狼群算法,但二者有許多不同.如在搜索方式上,前者模擬郊狼的成長、生與死,而后者模擬灰狼的等級制度和狩獵模式;在引導(dǎo)上,前者僅僅使用一頭最好的狼來引導(dǎo)其它狼成長,而后者使用3 頭最優(yōu)狼來引導(dǎo)其它狼搜索;在結(jié)構(gòu)上,前者復(fù)雜,后者簡單;在產(chǎn)生新解方式上,前者有兩種方式,后者只有一種方式等等.因此,COA 和GWO 各有優(yōu)勢和不足.為了彌補(bǔ)二者不足,本文將COA 和GWO 兩種狼群算法經(jīng)過改進(jìn)后進(jìn)行了有機(jī)結(jié)合,從而獲得一種性能優(yōu)越且高效的混合算法(HCOAG).

3.2 改進(jìn)的郊狼優(yōu)化算法

ICOA 主要包括高斯全局趨優(yōu)成長算子和動態(tài)調(diào)整組內(nèi)郊狼數(shù)方案.

3.2.1 高斯全局趨優(yōu)成長算子

為了提高郊狼成長后的社會適應(yīng)能力、組與組之間的信息共享程度及算法收斂速度,受Omran等[13]提出的全局最優(yōu)和聲搜索算法中趨優(yōu)策略及高斯分布的啟發(fā),對其組內(nèi)郊狼成長方式進(jìn)行改進(jìn),提出一種高斯全局趨優(yōu)成長算子.全局趨優(yōu)算子充分利用郊狼種群當(dāng)前全局最優(yōu)郊狼的狀態(tài)信息,使郊狼成長向當(dāng)前全局最優(yōu)郊狼趨近,提高開采能力,也使得組內(nèi)信息經(jīng)全局最優(yōu)解達(dá)到組間共享.高斯分布又稱為正態(tài)分布,與COA的均勻隨機(jī)分布[0,1]相比,可以增加搜索范圍,在一定程度上增強(qiáng)全局搜索能力.

在組內(nèi)郊狼成長過程中,在式(18)中引入趨優(yōu)算子和高斯分布隨機(jī)因子,具體見式(25)和式(26).

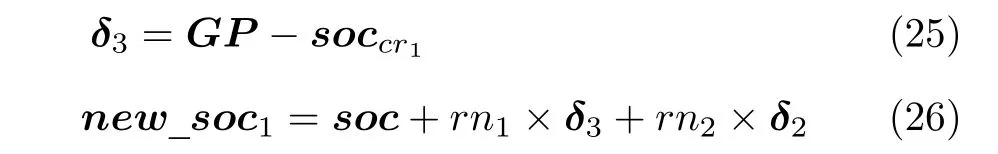
式(25)中,GP為當(dāng)前全局最優(yōu)郊狼的狀態(tài),δ3表示組內(nèi)隨機(jī)選取的一個郊狼狀態(tài) (cr1)與GP的差值.式(26)中,rn1和rn2是均值為0、方差為1的高斯(正態(tài))分布產(chǎn)生的隨機(jī)數(shù),new_soc1表示每頭郊狼在δ2和δ3的共同作用下成長產(chǎn)生的新狀態(tài)(新解).

從式(25)和式(26)可以看出,與COA 相比,在搜索前期,個體間差異大,縮放因子(高斯隨機(jī)數(shù))變化范圍大,故增強(qiáng)了探索能力.在搜索后期,雖然還是采用高斯隨機(jī)數(shù),但個體間差異小,δ2和δ3的值變小,故搜索范圍變小,強(qiáng)化開采能力.且由于采用全局最優(yōu)解引導(dǎo),故更增強(qiáng)了開采能力,同時上一組獲得的全局最優(yōu)解,會作用于下一組的郊狼成長,如此形成一種信息共享的正反饋?zhàn)饔?大幅度加快了收斂速度.另外,所有組內(nèi)郊狼成長后并行計(jì)算它們的適應(yīng)度值和優(yōu)勝劣汰,提高了運(yùn)行速度和穩(wěn)定性.

3.2.2 動態(tài)調(diào)整組內(nèi)郊狼數(shù)方案

如上文所述,COA 有多個參數(shù)需要調(diào)整,可操作性差.對于以上改進(jìn)的COA,主要有兩個參數(shù)Nc和Np對優(yōu)化性能影響較大.在N固定下,如果Nc確定,則Np=N/Nc,即Np越大,Nc越少,成長操作少,但全局解的作用逐組增強(qiáng),開采強(qiáng);反之,成長操作多,Np少,全局解的作用減弱,開采弱.為了提高COA的可操作性,本文對Np和Nc參數(shù)進(jìn)行動態(tài)調(diào)整.設(shè)N=100,則Np和Nc必須為100的因子,依據(jù)文獻(xiàn)[4],每組郊狼數(shù)不能超過14,所以Nc只能為4、5 和10.由于Nc不能少于3,這是因?yàn)榻M內(nèi)郊狼成長至少需要3 頭郊狼,包括隨機(jī)選取的兩頭郊狼和組內(nèi)最優(yōu)郊狼.當(dāng)Nc=4 時可選郊狼范圍受限制,所以Nc最可能的取值為5 和10,故具體的分配方式如圖2 所示,動態(tài)調(diào)整參數(shù)方案如算法2 所示.

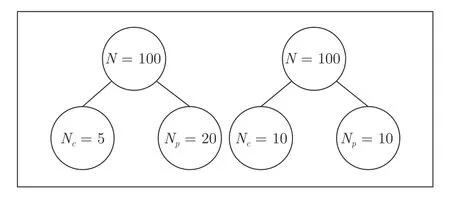
圖2 組數(shù) N p 與組內(nèi)郊狼數(shù) N c的分配圖Fig.2 Disposition graph of two parameters N c andNp

算法2.動態(tài)調(diào)整參數(shù)Nc和Np

在搜索后期,Nc=5,則Np=20,組數(shù)多,增強(qiáng)全局解的正反饋?zhàn)饔?局部搜索能力增強(qiáng);在搜索前期,Nc=10,則Np=10,組數(shù)少,減弱全局解的正反饋?zhàn)饔?全局搜索能力增強(qiáng).因此,動態(tài)調(diào)整組內(nèi)郊狼數(shù)參數(shù)不僅提高了可操作性,而且可以更好地平衡探索與開采能力.另外,在動態(tài)調(diào)整參數(shù)之后,隨機(jī)分組,如此可以省去郊狼被組驅(qū)離與接納這個過程,從而不需要調(diào)整參數(shù)Pe,因此提高了可操作性.

3.3 簡化的灰狼優(yōu)化算法

為了進(jìn)一步解決COA 存在搜索效率低和易陷入局部最優(yōu)的問題,本文引入GWO 搜索方式.首先提出一種精簡的GWO 搜索方式,即將式(6)～(11)與COA 組內(nèi)郊狼進(jìn)行融合并簡化,具體如式(27)～(29).

其中,tempc表示當(dāng)前組第c個郊狼的狀態(tài).NX1,NX2和NX3表示組內(nèi)郊狼分別在GP,alpha和cult的引導(dǎo)下獲得成長的情況.從式(27)～(29)可以看出,這3 個式子去掉了式(6)～(8)中的可調(diào)參數(shù)向量C,保留GWO的優(yōu)勢并克服其不足,即在SGWO 中,去掉C,無需調(diào)整c1,也省略了向量C的相關(guān)計(jì)算.所以,這種簡化的GWO 在保證其有較強(qiáng)開采能力的同時,提高了可操作性并降低了計(jì)算復(fù)雜度.為了更進(jìn)一步簡化計(jì)算,SGWO 直接采用COA 中的當(dāng)前全局最優(yōu)郊狼、組內(nèi)最優(yōu)郊狼和中值郊狼(組內(nèi)文化趨勢)的引導(dǎo)尋找最優(yōu)解,無需尋找組內(nèi)的第二和第三最優(yōu)郊狼,如此SGWO 與COA 達(dá)到了一種高效融合.為方便理解SGWO,關(guān)于GWO 中的灰狼等級情況與SGWO 中的等級情況的對比見圖3 所示.

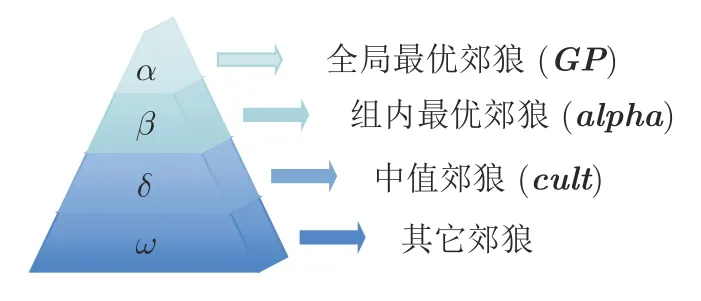
圖3 GWO 與SGWO的等級情況對比Fig.3 Comparison of hierarchies of GWO and SGWO

3.4 正弦交叉混合策略

為了平衡COA 組內(nèi)郊狼成長的探索與開采能力,本文采用正弦交叉策略將ICOA 與SGWO 有機(jī)混合.其中交叉策略是指在一定概率的情況下,兩個解進(jìn)行交叉得到一個新解.當(dāng)概率為零時,兩個解的維值不交換;當(dāng)概率為1 時,兩個解的維值全部交換,這兩種情況都不能產(chǎn)生新解.因此只有概率為一個適當(dāng)?shù)闹禃r,兩個解的交叉效果才會達(dá)到最好.其中使用正弦函數(shù)概率模型使得探索和開采都有良好的表現(xiàn),即使用正弦函數(shù)自適應(yīng)控制交叉概率CR(在0.5 附近前期小幅度波動,后期大幅度跳動)可以兼顧組內(nèi)郊狼的多樣性和收斂性[14],其計(jì)算式為

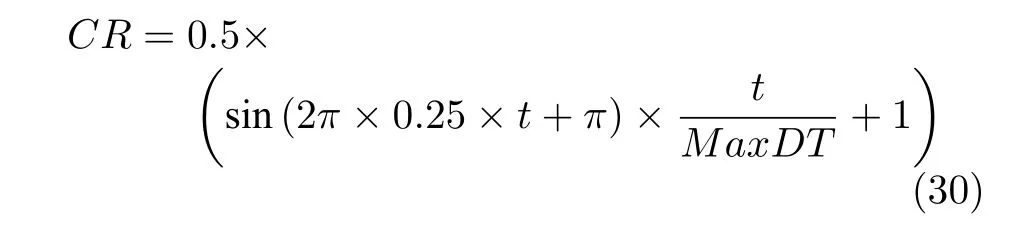
本文采用的正弦交叉策略見算法3 所示,在rand＜CR的概率下,組內(nèi)第c個郊狼D維中一些維的值采用SGWO 搜索方式獲取;反之,組郊狼的第c個郊狼D維中的其余維值采用高斯全局趨優(yōu)成長算子獲取.這種交叉策略具有如下特點(diǎn):1)增強(qiáng)了組內(nèi)各類郊狼的信息交流;2)交叉兩個新解,二者的信息融合獲得有別二者的新解,增強(qiáng)了新解的多樣性,降低陷入局部最優(yōu)的概率;3)前期在CR為0.5的附近小幅度波動,高斯全局趨優(yōu)操作和GWO 操作以近似等概率的方式產(chǎn)生新解,多樣性強(qiáng),強(qiáng)化探索能力;后期在CR為0.5的附近大幅度跳動,如此產(chǎn)生的新解以其中一種操作為主,多樣性降低,強(qiáng)化了開采能力.

算法3.正弦交叉策略

正弦交叉策略有機(jī)融合了兩種搜索方式,很好地平衡了成長過程的探索與開采能力.HCOAG的流程圖見圖4.

從圖4 可以看出,與COA 相比,HCOAG 主要有如下不同:1)成長方式采用正弦交叉策略融合高斯全局趨優(yōu)方式和SGWO 方式;2)組內(nèi)郊狼的適應(yīng)度值采用并行計(jì)算;3)動態(tài)調(diào)整參數(shù)方案;4)丟棄了郊狼被組驅(qū)離與接納的過程.

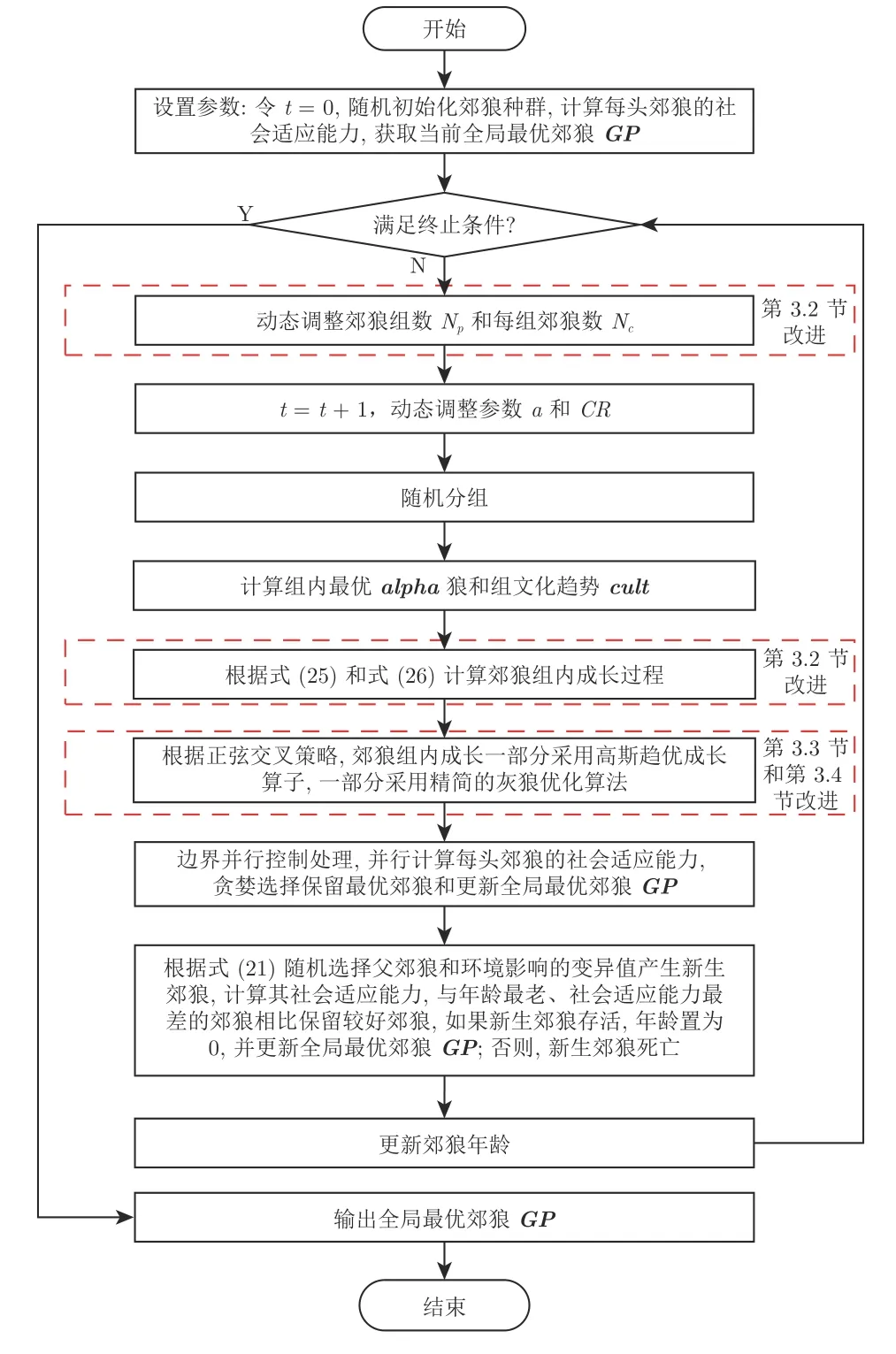
圖4 HCOAG 流程圖Fig.4 Flow chart of HCOAG

4 函數(shù)優(yōu)化實(shí)驗(yàn)結(jié)果與分析

4.1 實(shí)驗(yàn)環(huán)境配置及參數(shù)設(shè)置

為驗(yàn)證HCOAG的有效性,本文采用經(jīng)典基準(zhǔn)函數(shù)和來自CEC2017的復(fù)雜函數(shù)進(jìn)行優(yōu)化實(shí)驗(yàn).CEC2017 包括單峰函數(shù)(F1～F3)、多峰函數(shù)(F4～F10)、混合函數(shù)(F11～F20)和復(fù)合函數(shù)(F21～F30),詳細(xì)情況見文獻(xiàn)[15].實(shí)驗(yàn)環(huán)境采用主頻3.00 GHz的Inter(R)Core(TM)i5-7400 CPU 和內(nèi)存8 GB的PC 機(jī),操作系統(tǒng)采用64 位的Windows 10,編程語言采用MATLAB2017A.選取的對比算法包括GWO[3]、COA[4]、MEGWO (Multi-strategy ensemble GWO)[16]、DEBBO (Differential evolution and biogeography-based optimization)[17]、HFPSO(Hybrid firefly with PSO)[18]、SaDE (DE with strategy adaptation)[19]、SE04 (Spherical evolution)[20]、FWA (Fireworks algorithm)[21]和TLBO(Teaching-learning based optimization)[22].MEGWO 是最近提出的GWO 改進(jìn)算法,文獻(xiàn)[16]表明它優(yōu)于GWO 及其改進(jìn)版以及其他的SIOA.DEBBO是DE 與BBO的混合算法,文獻(xiàn)[17]表明它優(yōu)于DE 和BBO 及其他優(yōu)秀的SIOA.HFPSO 是PSO和FA的混合算法,文獻(xiàn)[18]表明它優(yōu)于PSO 和FA 等SIOA.SaDE 具有顯著優(yōu)秀性能,文獻(xiàn)[19]表明SaDE 優(yōu)于DE 等SIOA.SE04 是球形進(jìn)化算法的變體之一,文獻(xiàn)[20]表明SE04 顯著優(yōu)于GWO等算法.FWA 和TLBO 也是目前較為新型算法的代表.總之,這些對比算法具有較強(qiáng)的競爭性.

為公平起見,所有算法的公共參數(shù)設(shè)置相同.在CEC2017 上,依據(jù)文獻(xiàn)[15]的參數(shù)最佳推薦,D=30,最大函數(shù)評價(jià)次數(shù)10 000 ×D,獨(dú)立運(yùn)行51 次.在經(jīng)典函數(shù)的D=10 和D=30 上,MaxDT分別為100 和500,獨(dú)立運(yùn)行30 次.依據(jù)文獻(xiàn)[4]的推薦,COA的最佳參數(shù)設(shè)置為:N=100,Nc=5,Np=20. HCOAG的N也設(shè)置為100,Np和Nc無需調(diào)整,算法其他參數(shù)采用相應(yīng)文獻(xiàn)中推薦的最佳設(shè)置.

一般單峰函數(shù)用來考察一個算法的局部搜索能力,多峰函數(shù)考察其全局搜索能力,混合和復(fù)合函數(shù)考察其處理復(fù)雜問題的能力.本文采用均值(Mean)和方差(Std)分別評估一個算法的優(yōu)化性能和穩(wěn)定性.在解決極小值問題中,均值越小表示算法性能越好,方差越小表示算法穩(wěn)定性越好.另外,還采用了排名(Rank)方法.其評價(jià)標(biāo)準(zhǔn)是先比較算法獲得的均值,均值越小算法名次越好;在均值相同的情況下,再比較方差,方差越小算法名次越好.結(jié)果表中的“Count”表示排名為第一的總次數(shù),“Ave rank”表示平均排名情況,“Total rank”表示在“Ave rank”基礎(chǔ)上的總排名情況,最優(yōu)者用加粗字體表示.

4.2 與不完全算法的對比分析

為驗(yàn)證每個改進(jìn)對HCOAG 優(yōu)化性能的貢獻(xiàn),將HCOAG 與其不完全算法HCOAG5(Nc=5和Np=20的HCOAG)、HCOAG10(Nc=10和Np=10的HCOAG)、ICOA、SGWO、GWO 和COA 在CEC2017的30 維函數(shù)上進(jìn)行實(shí)驗(yàn),實(shí)驗(yàn)結(jié)果如表1 所示.

從表1 中可以看出,HCOAG5在單峰函數(shù)上獲得最好的結(jié)果次數(shù)最多,表明Np增大,在提高郊狼生與死的全局搜索能力的同時,大幅度提高了COA的開采能力,即HCOAG5中高斯趨優(yōu)成長和GWO 搜索都采用當(dāng)前全局最優(yōu)郊狼引導(dǎo),不僅獲得更好的全局最優(yōu)解,這種全局最優(yōu)解又作用于下一組郊狼的成長過程,如此形成正反饋機(jī)制:Np越大,開采越強(qiáng),收斂速度越快.但容易陷入局部最優(yōu),如在多峰函數(shù)上的表現(xiàn)不盡人意.HCOAG10在多峰函數(shù)上表現(xiàn)出了良好的優(yōu)化性能,表明Np變少,在提高組內(nèi)郊狼成長的局部搜索能力的同時,正反饋減弱,開采能力降低,即陷入局部最優(yōu)的概率也降低了.ICOA 中沒有精簡的GWO,整體來說優(yōu)于COA,表明對COA的改進(jìn)是有效的.SGWO在整體上優(yōu)于GWO,表明SGWO 提高了GWO搜索能力.與GWO 相比,COA的優(yōu)化性能更好,即COA 能更好地處理復(fù)雜優(yōu)化問題.在7 個算法中,HCOAG的平均排名為2.20,COA、GWO、HCOAG5、HCOAG10、ICOA 和SGWO的平均排名分別為5.23、6.87、3.10、2.60、3.07 和4.93,總排名的名次分別為6、7、4、2、3 和5.在HCOAG 與6 種對比算法中,HCOAG 獲得了最好的優(yōu)化性能,這也說明本文提出的算法是有效的.

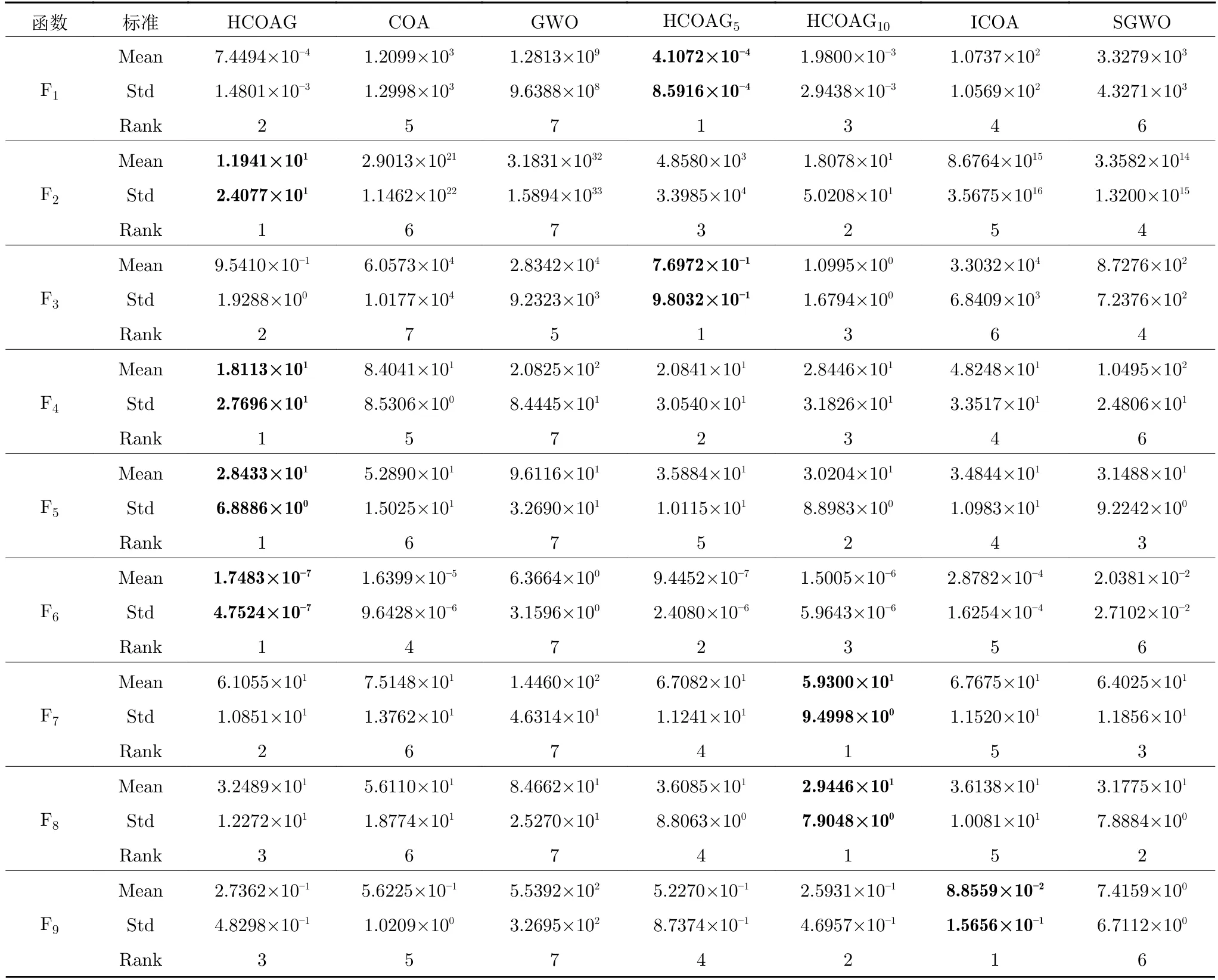
表1 HCOAG 與其不完全算法的結(jié)果對比Table 1 Comparison results of HCOAG and its incomplete algorithms

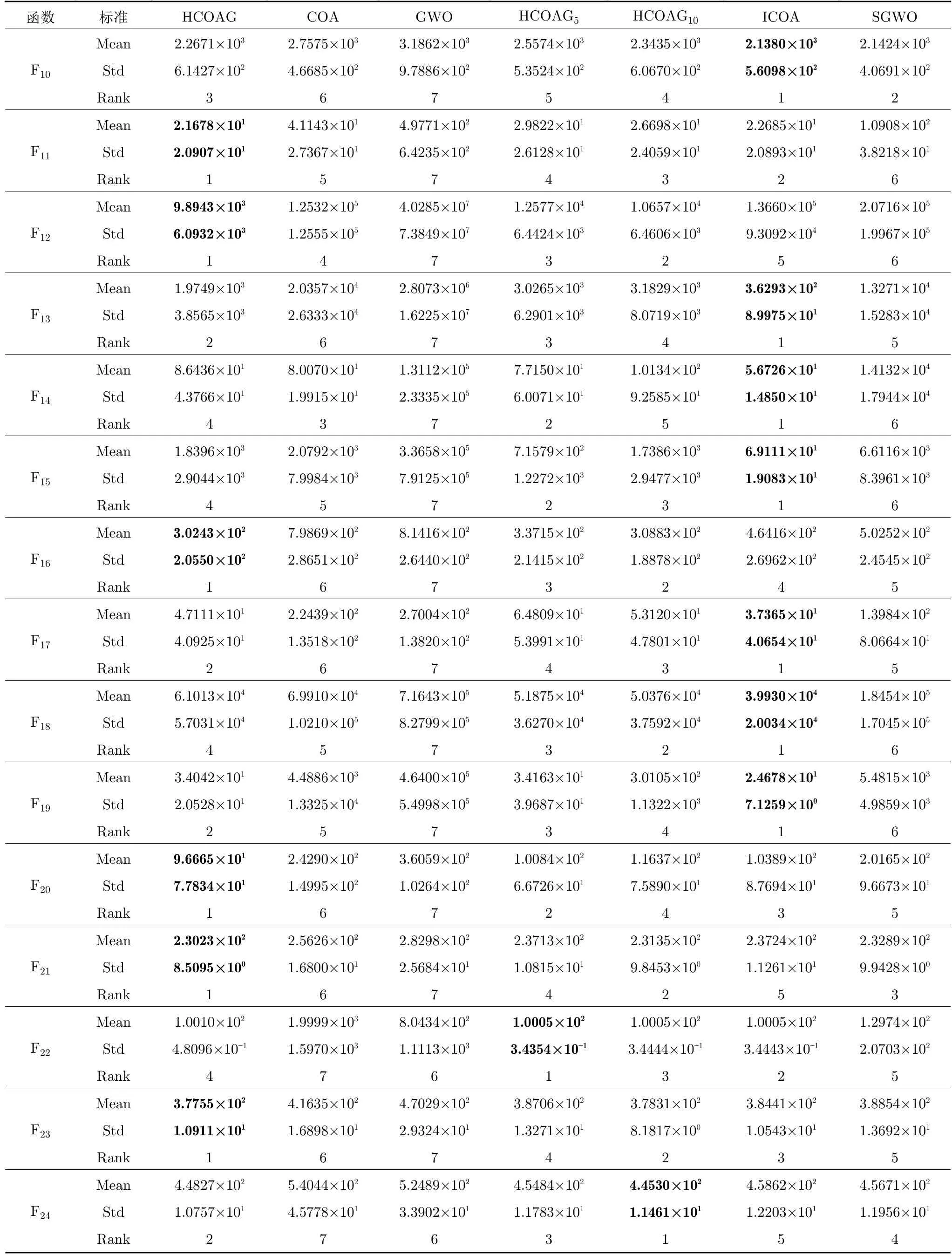
表1 HCOAG 與其不完全算法的結(jié)果對比 (續(xù)表)Table 1 Comparison results of HCOAG and its incomplete algorithms (continued table)

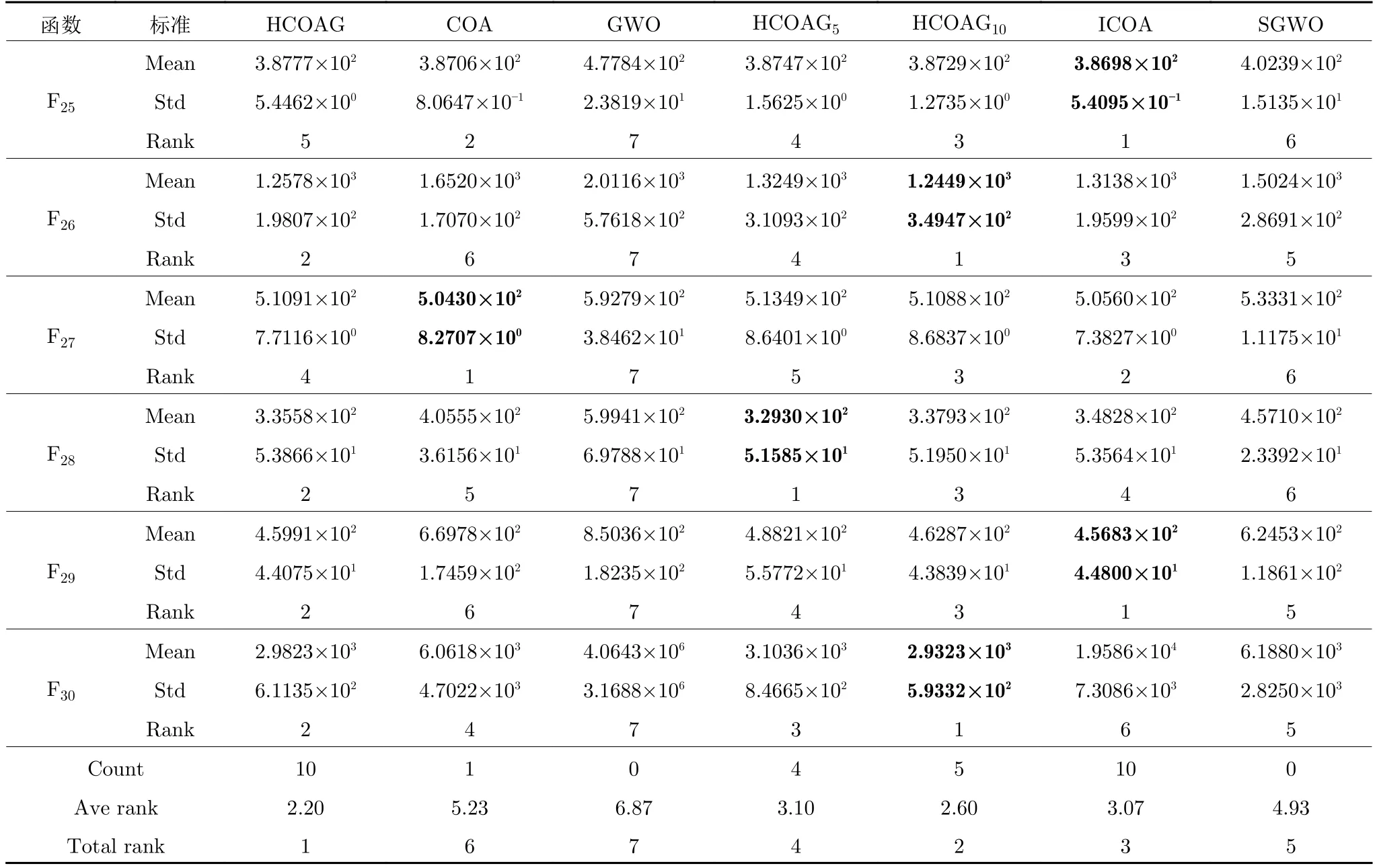
表1 HCOAG 與其不完全算法的結(jié)果對比 (續(xù)表)Table 1 Comparison results of HCOAG and its incomplete algorithms (continued table)

4.3 在經(jīng)典函數(shù)上的優(yōu)化性能對比

為驗(yàn)證HCOAG的性能,首先將其用于經(jīng)典函數(shù)的優(yōu)化實(shí)驗(yàn),并將其結(jié)果與COA、GWO、HFPSO和DEBBO的結(jié)果進(jìn)行對比,實(shí)驗(yàn)結(jié)果見表2.

為了能說明問題,選擇6 個經(jīng)典的、具有代表性的基準(zhǔn)函數(shù)的實(shí)驗(yàn)結(jié)果作為示例進(jìn)行分析和討論,這6 個函數(shù)的信息如表3 所示,其中f1～f3和f4～f6分別作為單峰函數(shù)和多峰函數(shù)的代表.在此實(shí)驗(yàn)中,由于HCOAG 是COA 和GWO的混合算法,故選擇COA 和GWO 作為對比算法.HFPSO和DEBBO 是目前兩種較為優(yōu)秀的混合算法,故選為HCOAG的對比算法.

從表2 可以看出,在D=10和D=30 上,COA無論是在單峰還是在多峰函數(shù)上優(yōu)化性能最差,說明COA 在處理這些經(jīng)典函數(shù)優(yōu)化問題上無優(yōu)勢.在單峰函數(shù)的均值和方差上,除了f3外,GWO 均優(yōu)于HCOAG 以及其他3 種對比算法,證明了GWO具有較好的開采能力.在多峰函數(shù)上,HCOAG的性能最佳,說明GWO 與全局搜索能力強(qiáng)的COA混合有效.

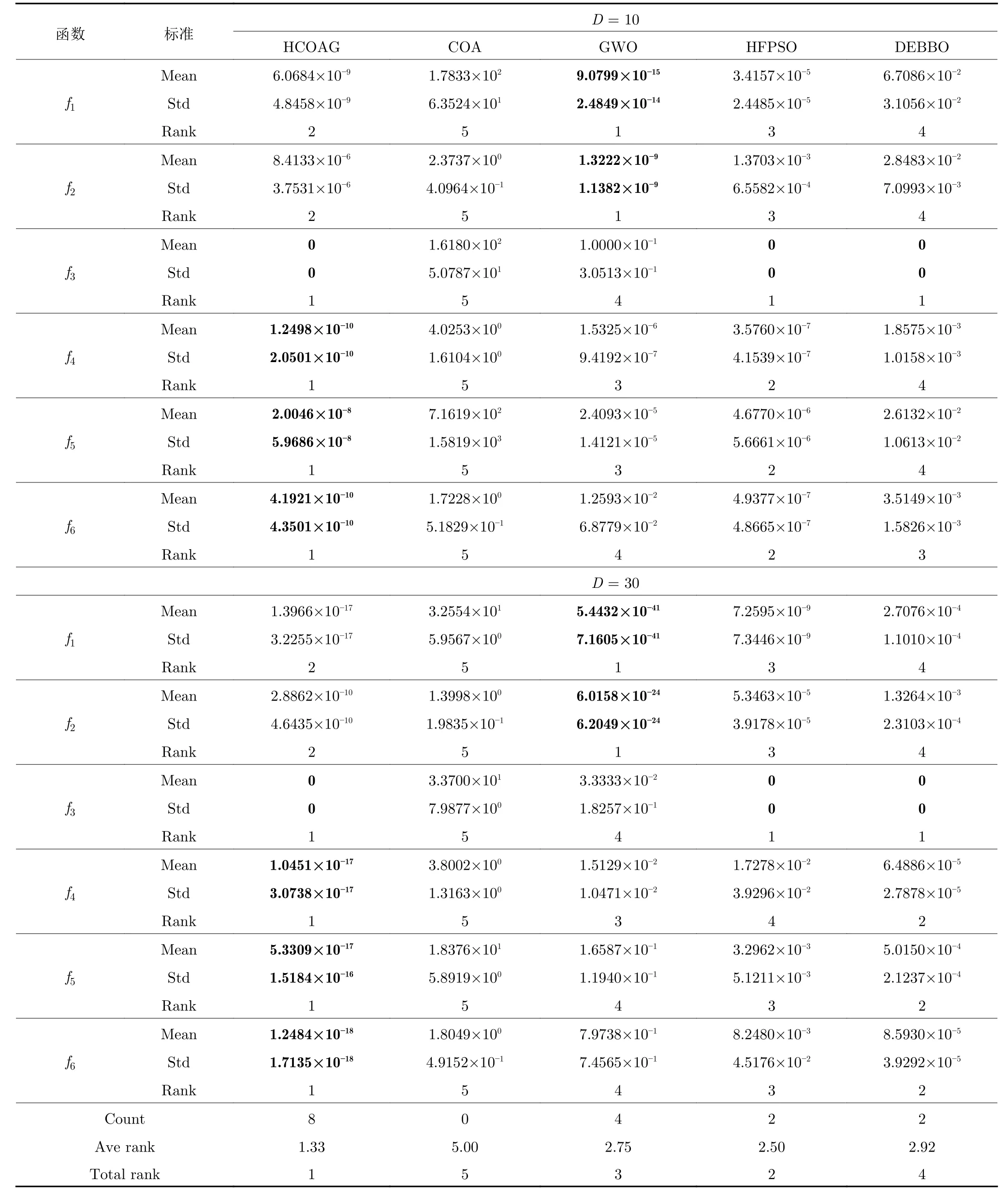
表2 在6 個經(jīng)典函數(shù)上的實(shí)驗(yàn)結(jié)果對比Table 2 Comparison results on the 6 classic functions

表3 6 個經(jīng)典函數(shù)的情況Table 3 Details of 6 classical benchmark functions

從整體上看,在D=10和D=30 上,HCO-AG的總體平均排名為1.33,其他算法的平均排名依次為:HFPSO (2.50)、GWO (2.75)、DEBBO(2.92)和COA (5.00).這些結(jié)果表明,HCOAG 不是對所有優(yōu)化問題都有絕對優(yōu)勢,在單峰函數(shù)上優(yōu)化性能稍差.而GWO 在單峰函數(shù)上具有優(yōu)勢,對HCOAG的性能具有一定的貢獻(xiàn).從整體上看,HCOAG 在經(jīng)典函數(shù)上具有較好的優(yōu)化性能.

為直觀顯示HCOAG、COA、GWO、HFPSO和DEBBO的收斂性能,給出了這5 個算法的收斂圖.限于篇幅,本節(jié)在D=30 上選取2 個單峰函數(shù)(f1和f2)和2 個多峰函數(shù)(f5和f6),如圖5 所示.在單峰函數(shù)上,與HCOAG、COA、HFPSO 和DEBBO算法相比,GWO 收斂速度更快,表現(xiàn)出更好的收斂性能.在多峰函數(shù)上,與COA、GWO、HFPSO和DEBBO 算法相比,HCOAG 表現(xiàn)出了更好的收斂性能.綜上所述,表2 和圖5 說明了GWO 具有較好的局部搜索能力和收斂性能,也部分證明了利用GWO 局部搜索能力強(qiáng)的優(yōu)勢對COA的混合改進(jìn)是必要和可行的.

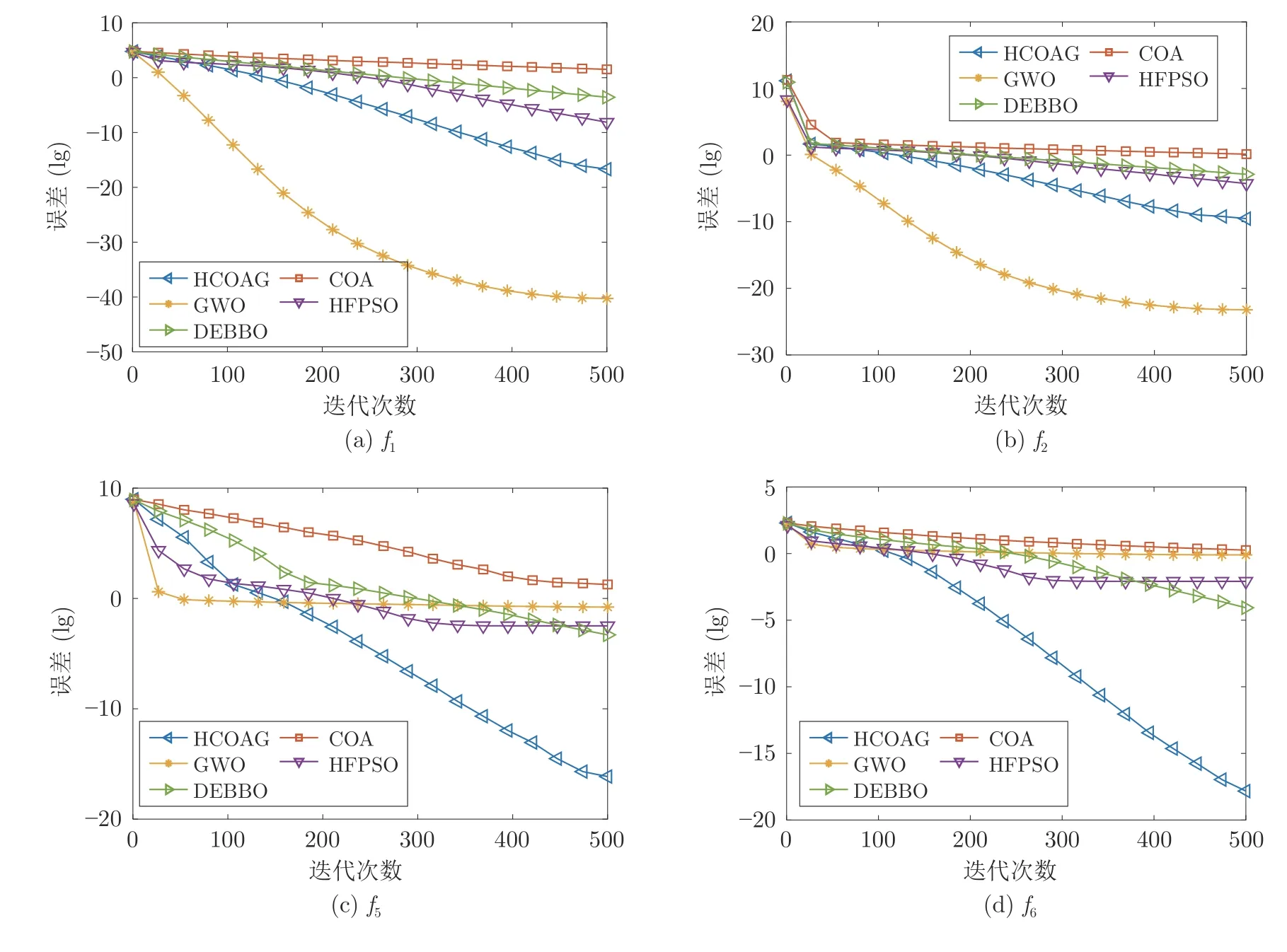
圖5 HCOAG 與對比算法在4 個經(jīng)典函數(shù)上的收斂圖Fig.5 Convergence curves of HCOAG and the comparison algorithms on the 4 classical benchmark functions

4.4 在CEC2017 復(fù)雜函數(shù)上的優(yōu)化性能對比

為了進(jìn)一步驗(yàn)證HCOAG的搜索能力,將其用在CEC2017 復(fù)雜函數(shù)上實(shí)驗(yàn),并將其結(jié)果與9 個代表性的先進(jìn)算法COA、GWO、MEGWO、HFPSO、DEBBO、SaDE、SE04、FWA 和TLBO的實(shí)驗(yàn)結(jié)果進(jìn)行比較,其結(jié)果見表4,其中SaDE和SE04的實(shí)驗(yàn)數(shù)據(jù)直接來自文獻(xiàn)[20].

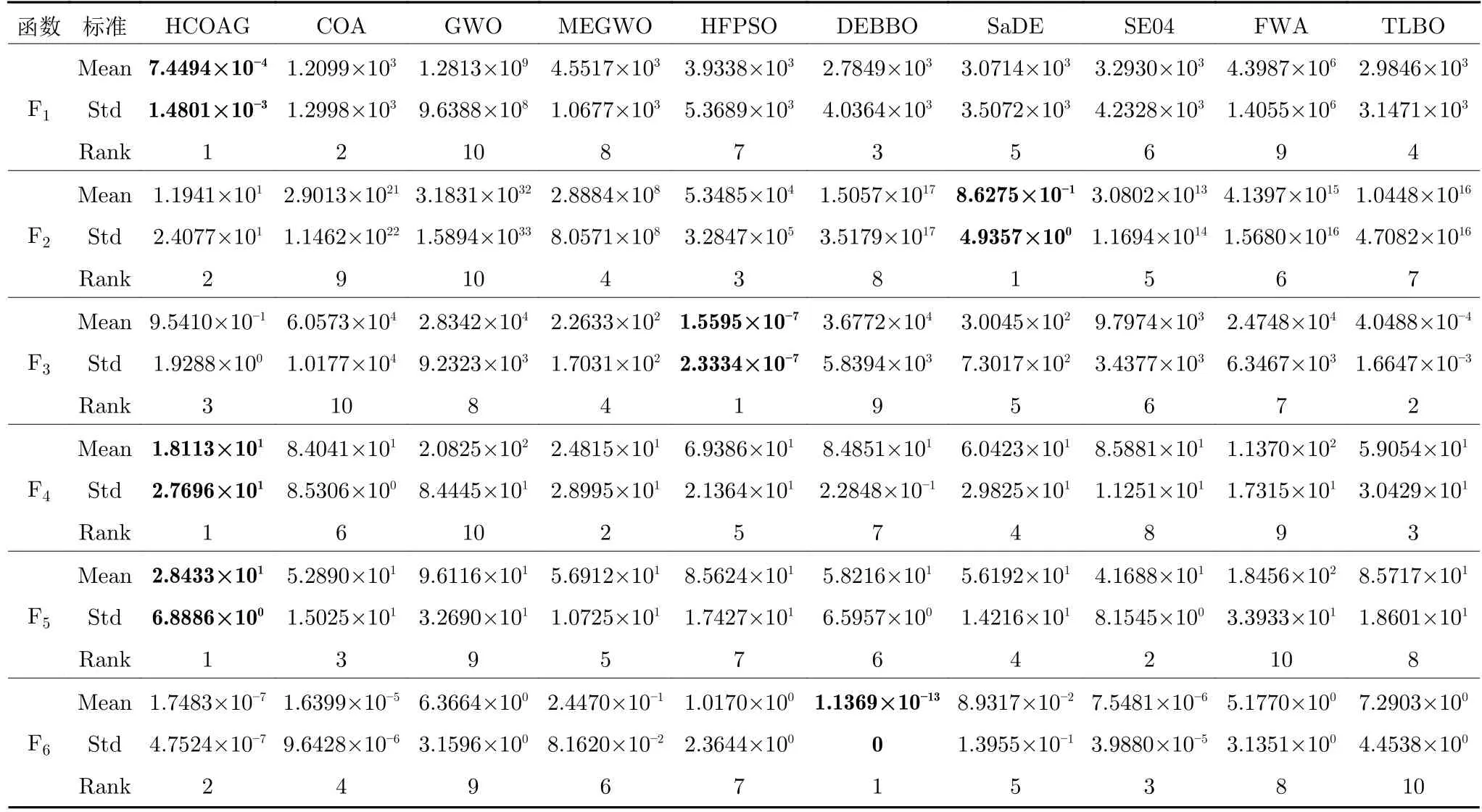
表4 在30 維CEC2017 復(fù)雜函數(shù)上的優(yōu)化結(jié)果對比Table 4 Comparison results on the 30-dimensional complex functions from CEC2017

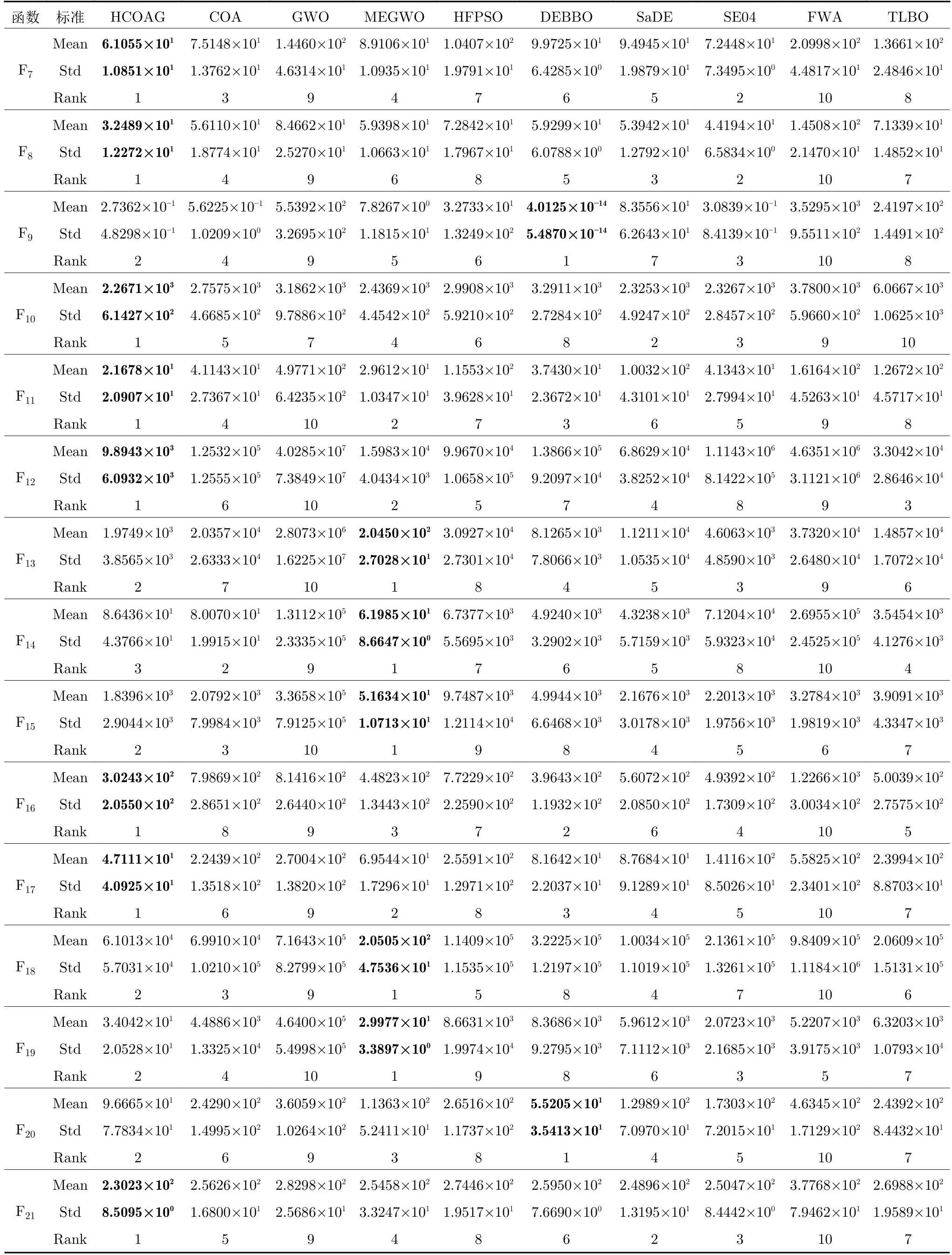
表4 在30 維CEC2017 復(fù)雜函數(shù)上的優(yōu)化結(jié)果對比 (續(xù)表)Table 4 Comparison results on the 30-dimensional complex functions from CEC2017 (continued table)

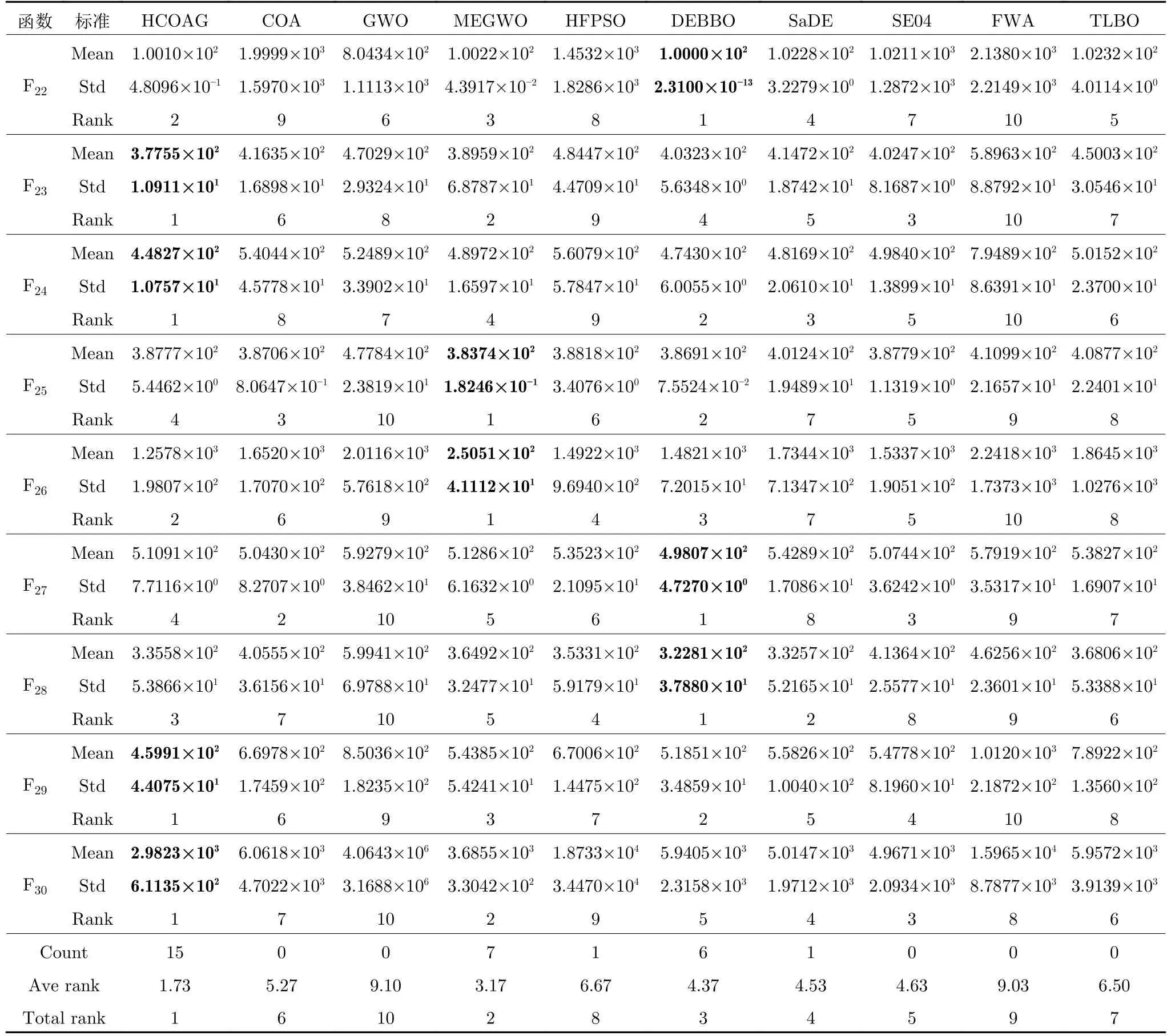
表4 在30 維CEC2017 復(fù)雜函數(shù)上的優(yōu)化結(jié)果對比 (續(xù)表)Table 4 Comparison results on the 30-dimensional complex functions from CEC2017 (continued table)

在均值和方差上,與MEGWO 相比,HCOAG 優(yōu)于23 次.與同為混合算法的HFPSO 和DEBBO 相比,HCOAG 分別優(yōu)于29 次和23 次.與SaDE 和SE04 相比,HCOAG 分別優(yōu)于28 次和29 次.與FWA 和TLBO 相比,HCOAG 分別優(yōu)于30 次和29 次.在總排名上,HCOAG 排名第一,接下來依次為MEGWO、DEBBO、SaDE、SE04、COA、TLBO、HFPSO、FWA、GWO.因此,HCOAG的性能優(yōu)于9 個先進(jìn)對比算法的性能.

4.5 收斂性能分析

為了驗(yàn)證HCOAG的收斂性能,給出HCOAG與COA、MEGWO、DEBBO、TLBO 和HFPSO在CEC2017 測試集中30 維函數(shù)的收斂圖.受篇幅所限,本文僅選取有代表性的函數(shù)作為示例進(jìn)行對比分析.在F1～F3中選取1 個單峰函數(shù),即F1,在F4～F10中選取F5,F7,F8這3 個多峰函數(shù),在F11～F20中選取F11,F12,F16,F17這4 個混合函數(shù),在F21～F30中選取F21,F23,F24,F29這4 個復(fù)合函數(shù),其收斂圖見圖6.

從圖6 中可以看出,在3 個函數(shù)F1,F5和F8上,隨著函數(shù)評價(jià)次數(shù)的增加,在收斂速度上,HCOAG 較對比算法要快得多,優(yōu)勢明顯.在其余9 個函數(shù)上,雖然HCOAG的收斂速度優(yōu)勢不是很明顯,但在收斂性能上也優(yōu)于其他對比算法.總之,無論在單峰函數(shù)和多峰函數(shù)上,還是在混合函數(shù)和復(fù)合函數(shù)上,HCOAG的收斂速度都比其他對比算法的收斂速度快,表明HCOAG 具有更優(yōu)秀的收斂性能.這些都說明,本文提出的高斯全局趨優(yōu)成長算子、動態(tài)調(diào)整組內(nèi)郊狼數(shù)方案以及簡化操作的GWO 搜索算子等的采用都為收斂速度的提升做出了貢獻(xiàn),這些策略的融合使用是有效可行的.

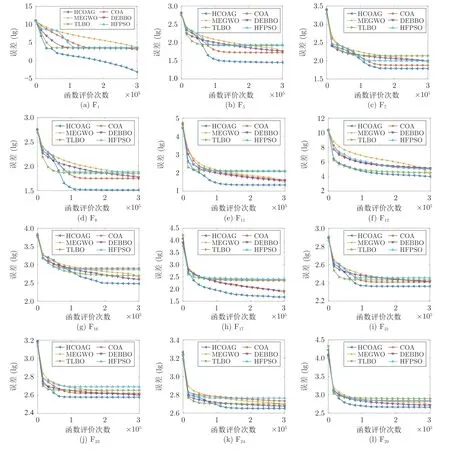
圖6 HCOAG、COA、MEGWO、DEBBO、TLBO 和HFPSO的收斂圖Fig.6 Convergence curves of HCOAG,COA,MEGWO,DEBBO,TLBO,and HFPSO

4.6 時間對比分析

為了考察HCOAG的運(yùn)行時間,直接采用第4.4 節(jié)的實(shí)驗(yàn).因?yàn)镠COAG 是COA 和GWO的混合算法,故僅記錄HCOAG、COA 和GWO 在30 維CEC2017 函數(shù)上的耗時,它們在獨(dú)立運(yùn)行30次獲得不同函數(shù)類型的平均耗時結(jié)果見圖7.橫坐標(biāo)為不同的函數(shù)類型,縱坐標(biāo)為平均時間(s).

從圖7 可以看出,在單峰函數(shù)上,HCOAG 耗時(2.4443 s)是COA 耗時(2.9988 s)的81.51%,GWO 耗時(2.4222 s)是HCOAG 耗時(2.4443 s)的99.10%;在多峰函數(shù)上,HCOAG 耗時(2.9211 s)分別是COA(3.5503 s)和GWO(2.9233 s)耗時的84.25%和99.92%;在混合函數(shù)上,HCOAG 耗時(3.6246 s)是COA 耗時(4.2034 s)的86.23%,GWO 耗時(3.4981 s)是HCOAG 耗時(3.6246 s)的96.51%;在復(fù)合函數(shù)上,HCOAG 耗時(6.1480 s)是COA 耗時(7.0897 s)的86.72%,GWO 耗時(6.0822 s)是HCOAG 耗時(6.1480 s)的98.93%.故無論是單峰函數(shù)和多峰函數(shù),還是混合函數(shù)和復(fù)合函數(shù),HCOAG的耗時都與GWO 耗時大致持平.其主要原因是:1)HCOAG 與GWO 都采用并行計(jì)算模式,但GWO 結(jié)構(gòu)簡單,而其產(chǎn)生新解的計(jì)算復(fù)雜度(見式(12))較高;2)HCOAG 雖然采用精簡GWO,但需要分組并在組內(nèi)尋優(yōu),結(jié)構(gòu)復(fù)雜,故二者耗時大致持平(HCOAG 耗時稍多于GWO的耗時).在耗時上,HCOAG 較COA 少,主要原因是:1)在成長過程的目標(biāo)函數(shù)評價(jià)上,后者采用串行計(jì)算,前者采用并行計(jì)算減少了運(yùn)行時間;2)雖然在成長過程中嵌入了GWO 搜索,但采用精簡的GWO 搜索方式并未增加多少計(jì)算成本;3)前者沒有郊狼被驅(qū)離和接納操作,節(jié)省了運(yùn)行時間;4)動態(tài)調(diào)整方案減少了生與死操作次數(shù).

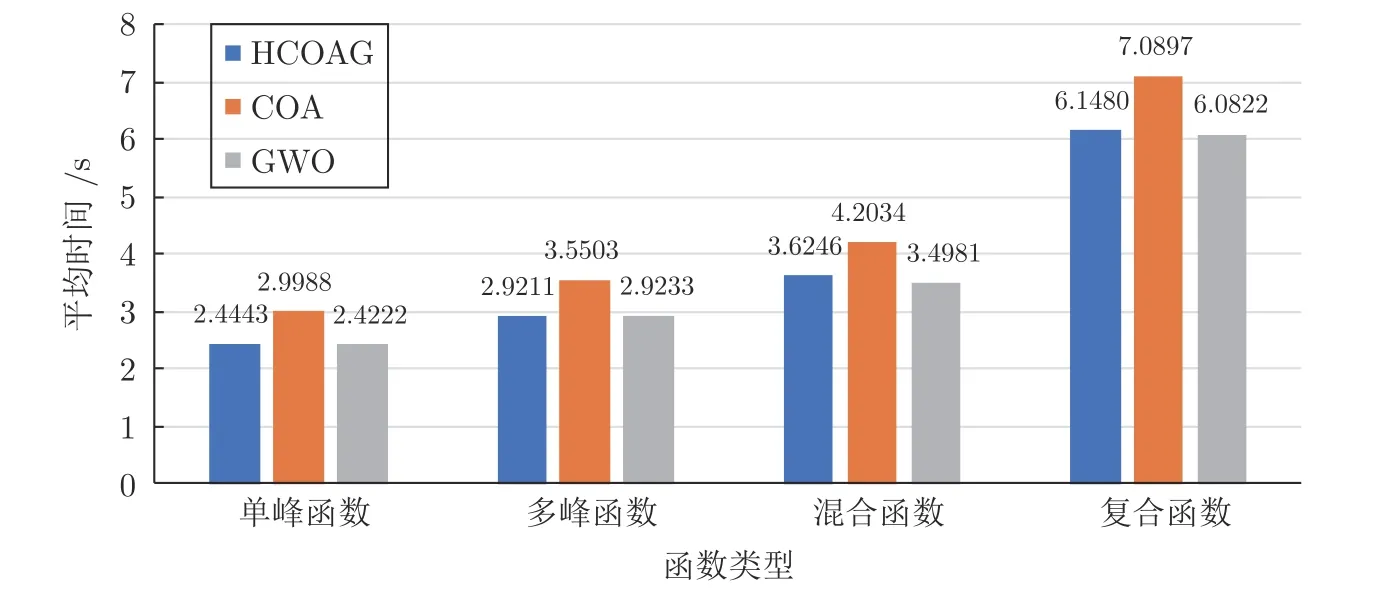
圖7 HCOAG 與COA、GWO 在不同類別函數(shù)上的平均時間對比圖Fig.7 Comparison bars of average time of HCOAG,COA,and GWO on different kinds of functions

綜合第4.3～4.6 節(jié),HCOAG 在較短的時間內(nèi)能獲得最好的優(yōu)化性能,說明了其優(yōu)化效率高.

4.7 上下界分析

為了能夠更充分地評價(jià)HCOAG的性能,本節(jié)對其進(jìn)行上下界分析,即在一個優(yōu)化問題上,獨(dú)立運(yùn)行一定次數(shù)后考察其最壞結(jié)果和最優(yōu)結(jié)果.

因?yàn)楸疚膶COAG 應(yīng)用于CEC2017 復(fù)雜函數(shù)集上,此函數(shù)集有30 個不同的優(yōu)化問題,其全局最優(yōu)解對應(yīng)的最優(yōu)值不同,故其獲得的上下界也不同.限于篇幅,在CEC2017 四類函數(shù)上分別選取了同樣的一個函數(shù)(F1,F5,F11,F29)進(jìn)行上下界討論,即在51 次的運(yùn)行結(jié)果中選擇最好值和最差值分別作為本文提出算法在該函數(shù)上的上下界,并與對比算法中結(jié)果最好的算法(在F1和F5上選用COA;在F11和F29上選用DEBBO)獲得的上下界進(jìn)行對比.

為了直觀和方便對比,對3 個算法獲得的結(jié)果進(jìn)行了統(tǒng)一的處理:即將每個算法每次獨(dú)立運(yùn)行結(jié)果減去理想的最優(yōu)函數(shù)值作為最終結(jié)果,讓每個函數(shù)的理想最優(yōu)值為0.在4 個函數(shù)上的上下界結(jié)果見表5.

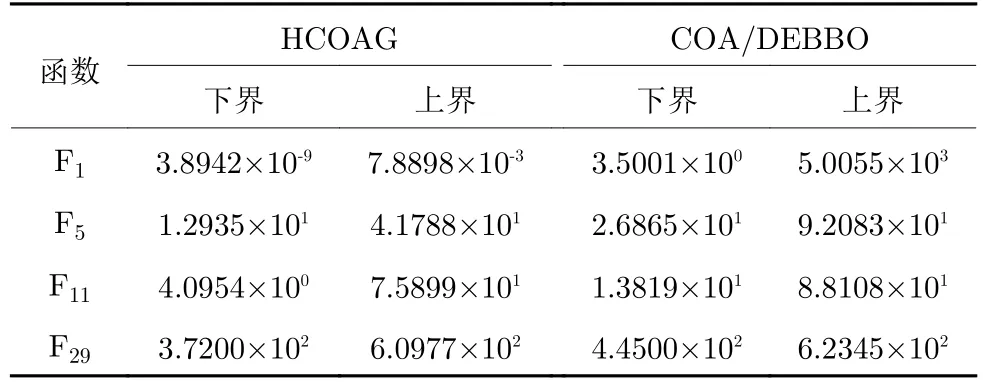
表5 在30 維CEC2017 復(fù)雜函數(shù)上的上下界結(jié)果對比Table 5 Comparison of upper and lower bounds on the 30-dimensional complex functions from CEC2017

從表5 可以看出,在4 個函數(shù)上,無論上界還是下界,HCOAG 都比對比算法小,說明本文提出的算法比對比算法好,也證明了本文提出算法的有效性.

4.8 漸進(jìn)收斂性分析

依據(jù)文獻(xiàn)[23]的隨機(jī)泛函分析方法原理,本節(jié)對HCOAG的收斂性進(jìn)行分析.從算法3的描述和HCOAG 流程圖(圖4)可以看出,HCOAG 由3個算子完成新解的產(chǎn)生,即高斯全局趨優(yōu)成長算子、簡化GWO 搜索算子以及生與死算子.高斯全局趨優(yōu)成長算子類似DE (Differential evolution)中的DE/rand-to-best/1/bin 變異算子;簡化GWO 搜索算子類似DE 中的DE/best/1/bin 變異算子;生與死算子相當(dāng)于遺傳算法中的變異算子.3 個算子產(chǎn)生的新解都采用貪心算法嚴(yán)格基于優(yōu)勝劣汰策略,通過淘汰新解與原解中較差者產(chǎn)生更優(yōu)的新一代個體.故對于最小優(yōu)化問題,HCOAG 評價(jià)函數(shù)序列為單調(diào)非遞增序列.為了證明HCOAG的漸近收斂性,首先做如下定義.

定義1.設(shè)Q(t)表示X(t)的中間群體,Vc,j(t+1)∈Q(t+1),則HCOAG 搜索算子定義如下:

高斯全局趨優(yōu)成長與簡化GWO 搜索混合算子定義為

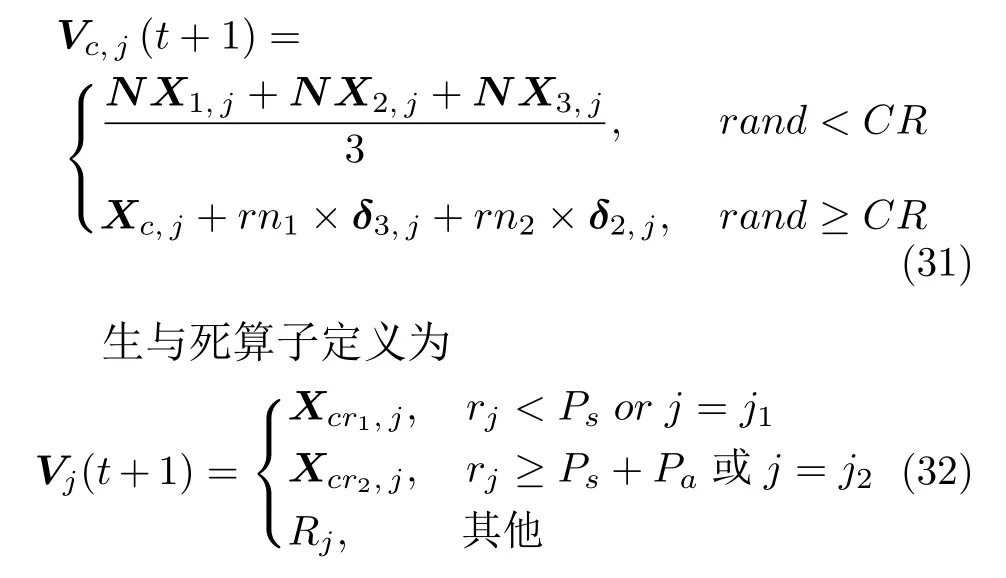
假設(shè)f(X)為 最小優(yōu)化函數(shù),解空間S=X|X={x1,x2,···,xD}且Lj ≤xj ≤Uj,j=1,2,···,D}為D維歐氏空間 RD的有界子空間.為了在進(jìn)行數(shù)值計(jì)算時不受計(jì)算精度的限制,設(shè)定HCOAG的計(jì)算精度保留到小數(shù)點(diǎn)后第k位數(shù)字.

定義2.兩種算子的混合策略是一種按照概率CR/D和(1-CR/D)對群體中個體向量的每一維分量分別采用簡化GWO 搜索算子和高斯全局趨優(yōu)成長算子以及在每一組中最差郊狼上采用生與死算子進(jìn)行重組變換的過程,它是解空間上的一種隨機(jī)映射ψ:Ω×S→S2,可定義為

定理1.HCOAG的一次迭代所形成的隨機(jī)映射ψ′是一個隨機(jī)壓縮算子.

再依據(jù)文獻(xiàn)[23]引理2,即可得到HCOAG 漸進(jìn)收斂的結(jié)論,即定理2.

定理2.設(shè)ψ′為HCOAG 形成的隨機(jī)壓縮算子,則ψ′具有唯一的隨機(jī)不動點(diǎn),即HCOAG 是漸進(jìn)收斂的.

4.9 Wilcoxon 符號秩檢驗(yàn)和Friedman 檢驗(yàn)

Wilcoxon 符號秩檢驗(yàn)方法[24]是一種非參數(shù)統(tǒng)計(jì)性檢驗(yàn)方法,目的在于檢驗(yàn)兩個樣本均值之間的顯著差異.其中p值由R+和R-計(jì)算可得,R+表示正秩總和,R-表示負(fù)秩總和,具體見式(34)和式(35),di為兩種算法在n個問題中第i個問題上的性能分?jǐn)?shù)的差值.當(dāng)HCOAG 算法與對比算法性能相同時,對應(yīng)的秩平分給R+和R-.為檢驗(yàn)HCOAG 與表4 中對比算法的顯著性差異,在軟件IBM SPSS Statistics 24 上實(shí)現(xiàn)Wilcoxon 檢驗(yàn),結(jié)果如表6 所示.表6 中,n/w/t/l表示在n個函數(shù)上HCOAG分別優(yōu)于對比算法w次,與對比算法相等t次,劣于對比算法l次.

從表6 可以看出,與COA 和GWO 相比,p值分別為1.3039×10-7和1.8626×10-9,均小于0.05,表明HCOAG 顯著優(yōu)于COA 和GWO,再一次說明COA 和GWO 二者的改進(jìn)與混合是有效的.HCOAG 與MEGWO、HFPSO、DEBBO、SaDE、SE04、FWA 和TLBO 相比的p值均小于0.05,表明HCOAG 也顯著優(yōu)于這些對比算法.

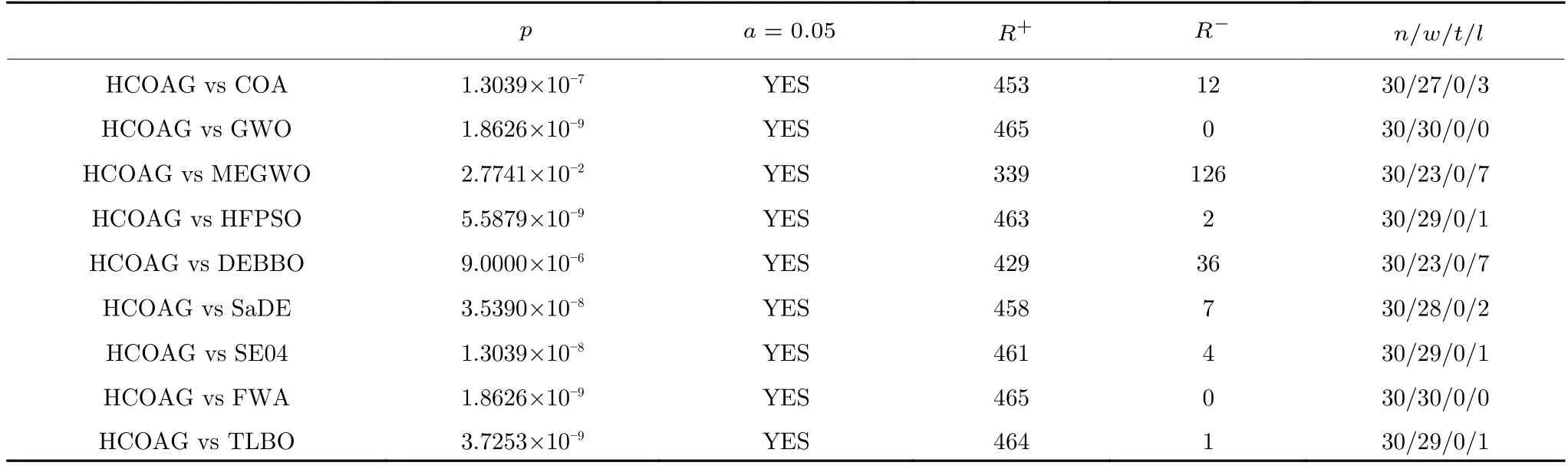
表6 Wilcoxon 符號秩檢驗(yàn)結(jié)果Table 6 Wilcoxon sign rank test results

Friedman 檢驗(yàn)是一種非參數(shù)雙向方差分析方法[24],目的在于檢測兩個或多個觀測數(shù)據(jù)之間的顯著性差異.具體實(shí)現(xiàn)過程分為3 步:1)收集每個算法或者問題的觀測結(jié)果;2)對于每個問題i的從1(最好結(jié)果)到k(最差結(jié)果)的排名值,定義為(1 ≤j≤k);3)在所有問題中求出每個算法的平均排名,得到最后排名在零假設(shè)下所有算法的行為相似(它們的秩Rj相等),Friedman統(tǒng)計(jì)值Ff的計(jì)算方式如式(36),當(dāng)n和k足夠大時(根據(jù)經(jīng)驗(yàn)n＞ 10,k＞ 5),它是按照k-1 自由度的x2分布的.為了再次驗(yàn)證HCOAG的顯著性,依據(jù)表4 對HCOAG 和對比算法在軟件IBMSPSS Statistics 24 上實(shí)現(xiàn)Friedman 檢驗(yàn),其結(jié)果如表7 所示.

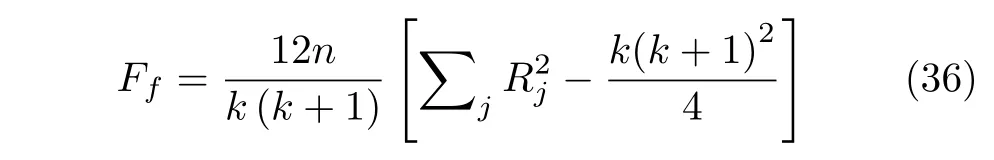
從表7 可以看出,在30 維復(fù)雜函數(shù)上,通過Friedman 檢驗(yàn)獲得的漸進(jìn)顯著性p值為6.3128×10-31,由于得到的漸進(jìn)顯著性小于0.01,所以在30維上HCOAG 與對比算法之間存在顯著性的差異.HCOAG 算法的秩均值(1.73)最小,隨后依次是MEGWO、DEBBO、SaDE、SE04、COA、TLBO、HFPSO、FWA 和GWO,表明HCOAG的優(yōu)化性能最好.結(jié)合Wilcoxon 符號秩檢驗(yàn)和Friedman 檢驗(yàn)結(jié)果可以得出,HCOAG 總體上明顯優(yōu)于先進(jìn)的對比算法.

表7 Friedman 檢驗(yàn)結(jié)果Table 7 Friedman test results

5 HCOAG 在K-Means 聚類優(yōu)化上的應(yīng)用

聚類在數(shù)據(jù)挖掘領(lǐng)域發(fā)揮著十分重要的作用,通過對聚類的數(shù)據(jù)分析可以得到數(shù)據(jù)的具體分布情況以及掌握數(shù)據(jù)類型的特點(diǎn)[25].其中,最常用的聚類方法是K-Means 方法[26],其在n個樣本數(shù)據(jù)中的具體實(shí)現(xiàn)過程如下:首先隨機(jī)產(chǎn)生K個初始聚類中心,然后計(jì)算每個樣本與各聚類中心的距離,接著將樣本與距離最近的聚類中心劃分到一個組內(nèi),形成K個組,最后重新計(jì)算每個組內(nèi)所有樣本的均值作為新聚類中心并進(jìn)行下一次劃分,如此迭代執(zhí)行劃分過程直到滿足終止條件為止.K-Means 方法具有原理簡單、可伸縮性好以及效率高等優(yōu)勢,但存在對初始點(diǎn)敏感和易陷于局部最優(yōu)等問題.目前已有研究將SIOA 運(yùn)用到K-Means 聚類中,很好地解決了K-Means 算法存在的一些問題[25,27].本節(jié)采用HCOAG 優(yōu)化K-Means 聚類以解決其對初始點(diǎn)敏感等問題,其中,目標(biāo)函數(shù)的定義為

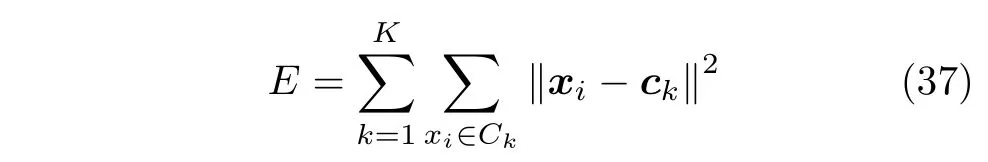
其中,E是數(shù)據(jù)集中所有數(shù)據(jù)點(diǎn)到所屬聚類的聚類中心的距離和,K是聚類中心個數(shù),ck是第k個聚類中心位置,Ck是第k個聚類簇,xi是聚類族Ck中第i個數(shù)據(jù)點(diǎn).將HCOAG 應(yīng)用到K-Means上,首先假設(shè)每頭郊狼由k個聚類中心組成,則解向量的維數(shù)應(yīng)等于k× 數(shù)據(jù)樣本的特征數(shù),目標(biāo)函數(shù)采用式(37);接著執(zhí)行HCOAG,直到滿足算法的終止條件,輸出最優(yōu)聚類中心.

實(shí)驗(yàn)采用UCI 數(shù)據(jù)庫(http://archive.ics.uci.edu/ml/datasets.php)中7 個標(biāo)準(zhǔn)數(shù)據(jù)集(見表8 第1 列)來驗(yàn)證HCOAG 在K-Means 聚類優(yōu)化上的有效性,數(shù)據(jù)集名稱后的括號內(nèi)的數(shù)字為樣本數(shù)、屬性數(shù)和聚類數(shù).選取的5 個對比算法包括:COA、MEGWO、HFPSO、擅長聚類優(yōu)化的改進(jìn)的粒子群優(yōu)化算法(Improved PSO,IPSO)和改進(jìn)的遺傳算法(Improved genetic algorithm,IGA).其中,IPSO 和IGA 來自“http://yarpizcom/64/ypml101-evolutionary-clustering”.所有算法的公共參數(shù)設(shè)置相同:N=50,MaxDT=200,Num=30.表8是6 種算法獨(dú)立運(yùn)行30 次獲得的均值、方差和排名結(jié)果.

從表8 可知,HCOAG 在7 個數(shù)據(jù)集上的均值和方差得到排名第一5 次,其次是HFPSO 和IPSO 均為1 次,COA、MEGWO 和IGA 均獲得0次第一.HCOAG的平均排名為1.43,其他算法的平均排名順序依次為:IPSO、IGA、MEGWO、HFPSO 和COA.以上結(jié)果都表明HCOAG 在KMeans 聚類上的優(yōu)化性能最好.總之,HCOAG 在K-Means 聚類優(yōu)化中獲得競爭性的優(yōu)化性能,能夠更好地處理聚類優(yōu)化問題.

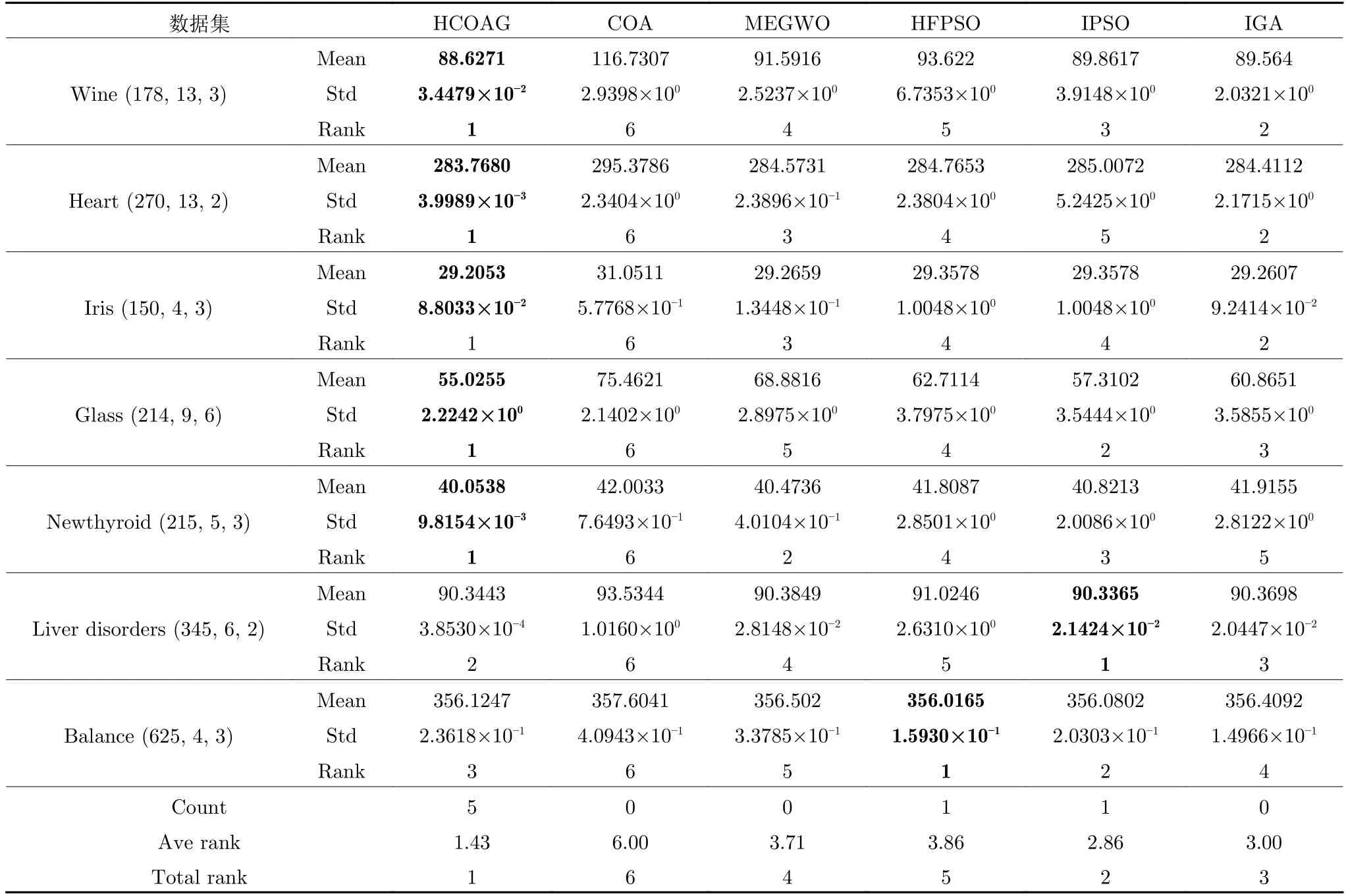
表8 6 種算法在K-Means 聚類優(yōu)化上的結(jié)果對比Table 8 Comparison results of the 6 algorithms on K-Means clustering optimization

6 結(jié)束語

針對COA 存在的不足,本文提出了一種COA與GWO的混合算法(HCOAG).首先,改進(jìn)COA(ICOA).1)在成長過程中,提出一種高斯全局趨優(yōu)成長算子,提高了搜索能力;2)提出一種動態(tài)調(diào)整組數(shù)方案,搜索前期采用較少組數(shù),減弱全局最優(yōu)解的正反饋?zhàn)饔?強(qiáng)化探索能力,后期采用較多組數(shù),增強(qiáng)全局最優(yōu)解的正反饋?zhàn)饔?強(qiáng)化開采能力,并提高可操作性.然后,對GWO 進(jìn)行改進(jìn),提出了一種精簡的GWO (SGWO),在發(fā)揮其局部搜索能力強(qiáng)的優(yōu)勢同時,提高了可操作性.最后,采用正弦交叉策略將ICOA 與SGWO 有機(jī)融合,很好地平衡了組內(nèi)郊狼的探索與開采能力,從而獲得了最佳優(yōu)化性能.大量經(jīng)典函數(shù)與CEC2017復(fù)雜函數(shù)優(yōu)化的實(shí)驗(yàn)結(jié)果表明,在經(jīng)典函數(shù)上,COA不及GWO;在復(fù)雜函數(shù)上,GWO 不及COA;而HCOAG 在兩類優(yōu)化問題上都有更好的性能,說明二者混合有必要和有效;與其他先進(jìn)的對比算法相比,HCOAG具有更好的優(yōu)化性能.K-Means 聚類優(yōu)化結(jié)果表明,與對比算法相比,HCOAG 獲得了競爭性的優(yōu)化性能.

總之,與COA 相比,HCOAG 具有如下優(yōu)勢:1)普適性強(qiáng),經(jīng)典函數(shù)和復(fù)雜函數(shù)優(yōu)化以及聚類優(yōu)化3 組實(shí)驗(yàn)結(jié)果表明,HCOAG 都有更好的表現(xiàn);2)耗時少,因此有更好的搜索效率;3)更好的收斂質(zhì)量;4)更強(qiáng)的穩(wěn)定性和魯棒性,5)可操作性更強(qiáng).

COA 是最近提出的一種SIOA,尚有許多地方需要探討和完善,本文僅是一種混合改進(jìn)研究的嘗試.未來將進(jìn)一步改進(jìn)COA,對其進(jìn)行深入的理論研究,并拓展其應(yīng)用領(lǐng)域.