考慮壓密效應的節泡型土釘抗拔力計算模型

李 煜，彭 銳，葉新宇，張 升

(1.中南大學 土木工程學院，湖南 長沙 410075；2.武漢地鐵運營有限公司，湖北 武漢 430030)

土釘支護是路基邊坡加固，基坑開挖，擋土墻等工程中最主要的支護方式[1-3]，而壓密注漿是土釘支護中應用最廣泛的一種注漿方法[4]。特別是通過在注漿口綁扎土工織物或膜，可以防止漿液滲透和劈裂擴散，達到控制注漿效果的目的[5]。相關研究已開展較多，Soga等[6]通過改進的固結儀研究壓實注漿對黏土固結比的影響，發現影響土體固結是漿液注入點周圍土體產生較大的應力集中。Yin等[7]提出了一種考慮土體膨脹，上覆土壓力和注漿壓力因素下計算土釘-土界面最大剪應力方法。張忠苗等[8]通過考慮壓濾效應開發一種模擬試驗裝置來研究壓密注漿時柱(孔)在黏土中擴張的機理。Wang等[9]通過設置漿液不滲透的設備來研究壓實注漿產生的壓密效應對孔隙比和超孔隙水壓力的影響。Nie等[10]通過二維不連續變形(2D-DDA)數值方法研究錨桿形狀與錨桿-砂漿黏結強度之間的關系。周子龍等[11]通過顆粒流方法來模擬壓密注漿過程中漿液與土體之間的作用機理，認為注漿壓力是影響壓實注漿方法的重要因素。上述研究主要針對壓密注漿與周圍土體相互作用，但壓密注漿對土釘/樁的承載力提高鮮有進一步探究。

黃明華等[12]建立荷載傳遞非線性的錨桿拉拔計算方法。Yin等[13]通過現場試驗發現壓密注漿對土釘周圍土體有壓密效應，并認為土體密實化是土釘抗拔力強化的主要原因。楊淼等[14]通過在樁身注漿形成竹節的手段來提高樁徑影響范圍的基礎上，研究擴張的竹節對樁側摩阻力的影響。張旭輝[15]將漿液壓密注漿到囊袋中，得到漿囊袋直徑可改善土釘的受力狀態和注漿體的長度可以提高土釘抗拔能力的結論。Wang等[16]設置一種注漿后在綁扎乳膠膜的注漿口形成節泡形狀的新型土釘，通過室內試驗發現節泡型土釘比傳統壓密注漿土釘具有更好的抗拔性能。Ye等[17]通過對節泡型壓密注漿土釘進行室內抗拔試驗,研究注漿壓力、飽和度對節泡型注漿土釘抗拔性能的影響。同時，Ye等[18-19]結合數值模擬與室內試驗結果，探討單節泡、多節泡對節泡型土釘抗拔規律。由此看出，壓密注漿土釘的壓密效應和抗拔機理已有較多研究成果，但如何定量描述壓密效應與注漿壓力之間變化關系和建立節泡型壓密注漿土釘抗拔力計算方法還有待進一步研究。

基于此，本文提出一種考慮壓密效應的節泡型壓密注漿土釘抗拔力計算模型，該模型能夠描述壓密效應對土釘抗拔力的強化作用。首先，基于有/無壓密效應兩組試驗，分析壓密效應強化抗拔力的機理；其次，采用指數模型描述注漿壓力與壓密效應間的非線性關系；再次，基于能量平衡理論建立抗拔力計算模型，通過對比試驗結果，驗證模型的合理性；最后，通過分析相關參數的變化，探討了壓密效應對節泡型土釘抗拔力的影響。本研究可為節泡型土釘的設計及工程應用提供有價值的參考。

1 基于壓密效應節泡型土釘能量平衡方程

1.1 試驗結果分析

Ye等[17]通過室內模型試驗得到節泡型土釘有/無壓密效應的抗拔力結果對比見圖1。由圖1可知，在注漿壓力相同時，有壓密效應的抗拔力與位移曲線在無壓密效應的上面，即相同的抗拔位移時，有壓密效應的土釘抗拔力較無壓密效應的高。節泡型土釘有/無壓密效應的抗拔力區別主要體現在0～50 mm的拉拔位移上，如注漿壓力GP為500、600 kPa的抗拔力相差分別為34.82%、44.58%，隨后在50～150 mm位移時，抗拔力相差分別降到5.74%、14.37%，在大于150 mm位移后，抗拔力相差分別為5.08%、4.33%。由于注漿形成節泡時造成節泡周圍土體致密化，致密化提高節泡周圍土體干密度ρd，致密化范圍為150 mm左右[20]，壓密效應示意見圖2，從而提高節泡型土釘抗拔力。

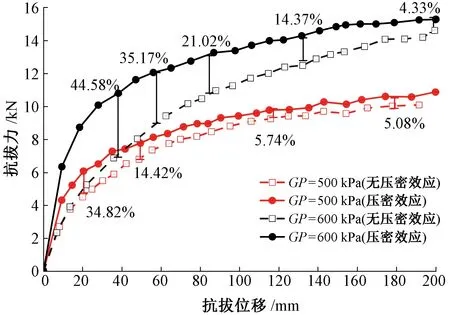
圖1 壓密效應與無壓密效應的抗拔力-位移

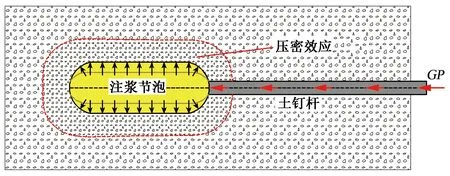
圖2 節泡型土釘壓密效應示意

圖 3給出室內抗拔試驗拉拔過程中節泡面周圍砂土的密度隨注漿壓力的變化關系，通過分析得出，注漿壓力使節泡面附近的土體的密度增加，即產生壓密效應，因而壓密效應的抗拔力發揮速率增快，Wang等[20]也發現壓密效應的存在。因此，非線性模型更能說明密度與注漿壓力的變化關系。

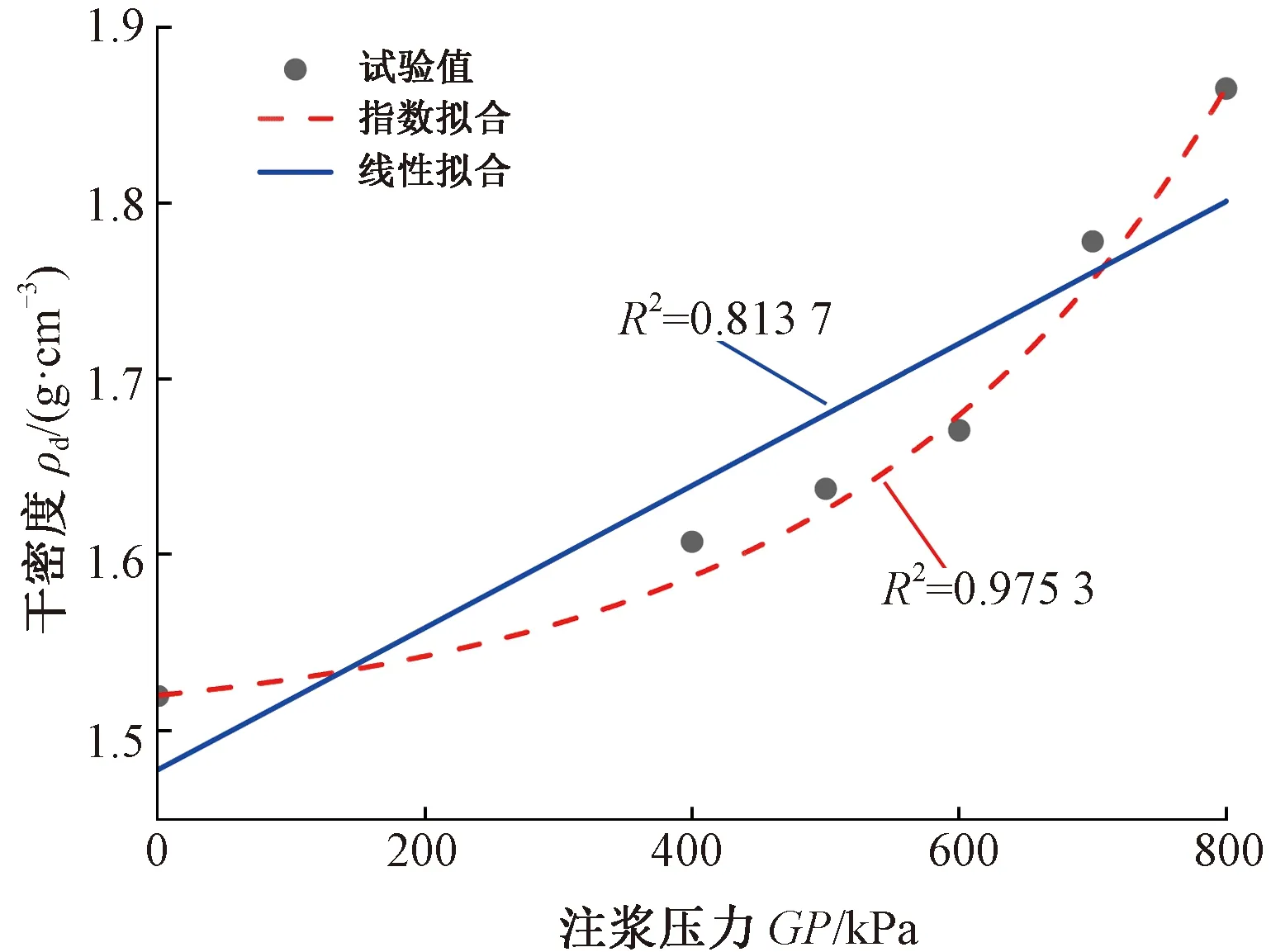
圖3 注漿壓力與干密度變化關系

1.2 考慮壓密效應模型建立

為進一步研究壓密效應的作用機理，分析壓縮模量與注漿壓力之間關系，見圖4。

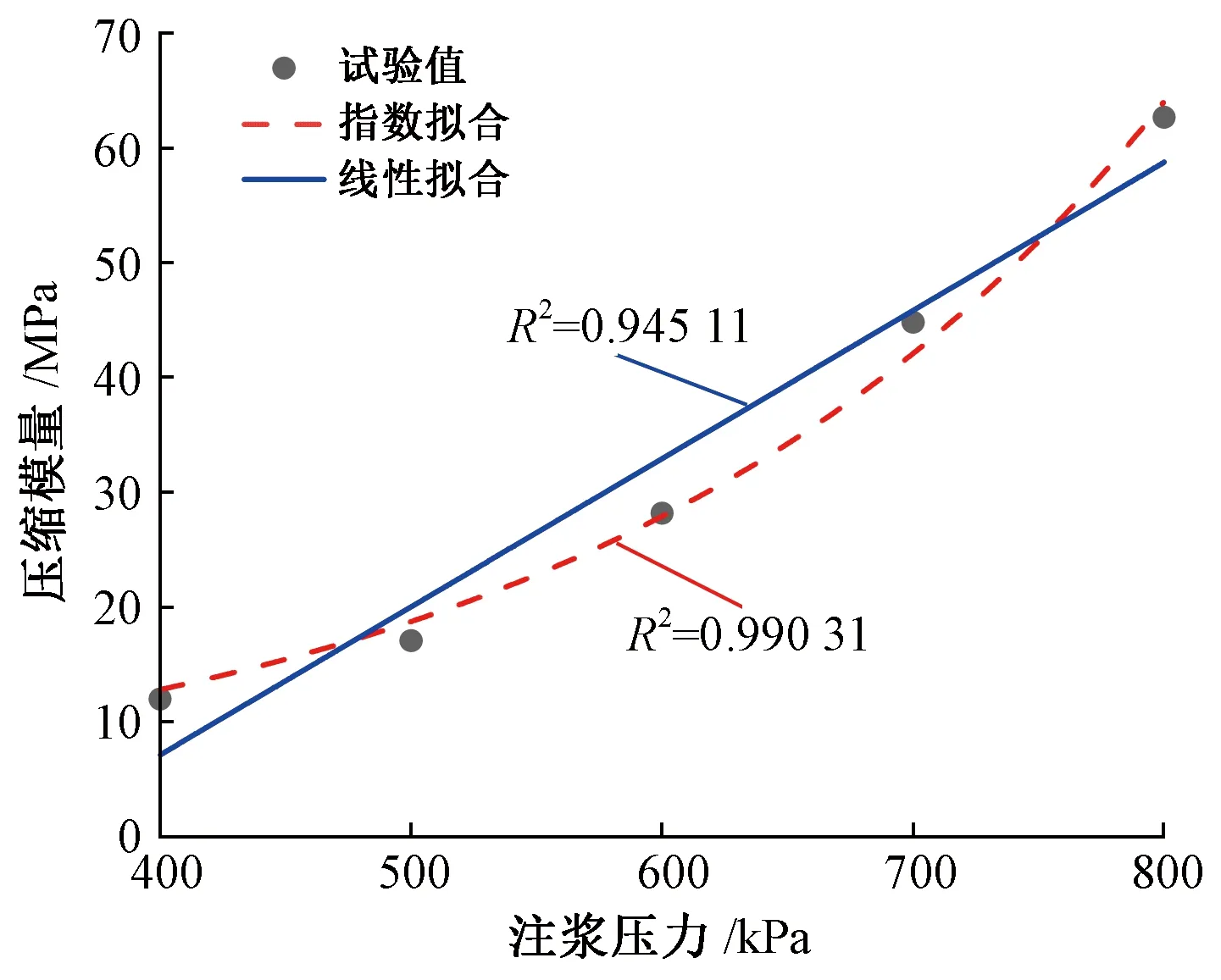
圖4 注漿壓力與壓縮模量變化關系

由圖 4分析得出，壓縮模量與注漿壓力的變化關系呈指數型變化，這與文獻[21]得到壓縮模量與注漿壓力的變化關系是非線性的結果是一致的，因此，本文采用指數模型來考慮壓密效應對土體參數的非線性變化，即：

Es=E0e(GP-GP0)/(μ1·GP0)

(1)

式中：μ1為速率因子，是關于周圍土體類型的參數，由于砂土不具有黏聚力，故一般砂土(0.8左右)比黏土取值小(小20%左右)[22]，本文砂土中取值0.7；GP為注漿壓力；E0為注漿壓力GP0時的壓縮模量，即初始壓縮模量，且注漿壓力GP0時退化為無壓密效應表達式；GP0為土釘節泡形成的注漿壓力臨界點，與土釘的埋深、周圍土體壓實度、漿液稠度等有關，本文根據試驗取320 kPa，進而能夠計算無壓密效應的抗拔力。因為漿液在較小壓力時由于注漿壓力損失及周圍土體的約束，難以有效注入形成節泡。幾組模型試驗證實在注漿壓力小于400 kPa時，漿液極難注入節泡。

根據文獻[23]，得到節泡面和土釘桿的雙曲線模型初始斜率1/ak為

(2)

節泡弧面壓力的雙曲線模型初始斜率1/ak為

(3)

式中：R為土釘的半徑；R0為土釘半徑的影響范圍；E1、G1分別為土體壓縮、剪切模量，根據文獻[24]等研究得到ln(R0/R)的值為3～5，本文取為3。

通過對壓密效應的作用機理分析以及壓密效應模型的建立，即可得到考慮壓密效應壓密注漿土釘側阻力與土體相對位移作用模型圖(圖 5)，相比無壓密效應的區別是初始斜率變大(即1/a1變大)，其函數表達式為

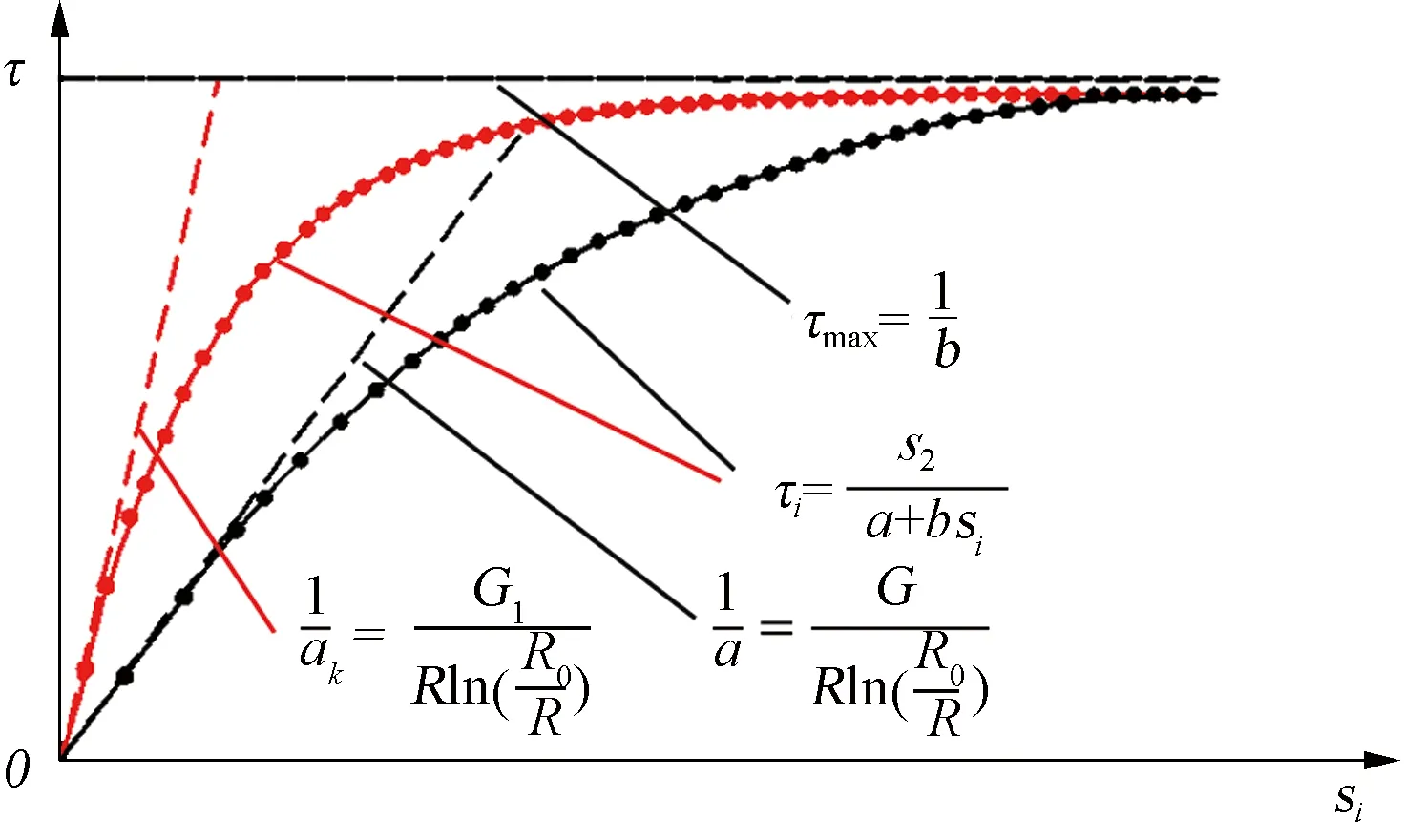
圖5 雙曲線模型

(4)

式中：a1、b分別為雙曲線模型參數；1/b為土體的極限抗剪強度；si為任意一點抗拔位移；τi為抗拔位移，是si的剪切強度。

節泡面和土釘桿的參數1/bk表達式為

1/bk=τmaxk=1

(5)

節泡弧面的參數1/bk表達式為

1/bk=σultk=2

(6)

式中：τmax為土體的極限抗剪強度；σult為土體的極限抗壓強度。

1.3 節泡型土釘受力分析

由于節泡型壓密注漿土釘存在節泡，采用以往求解方法來考慮變截面土釘的受力狀態變得復雜，且將桿單元的受力平衡方程和位移協調方程進行聯立求解時求解效率低。因此，本文采用能量法來研究整個土釘-土系統對象，則土釘-土系統總能量Π由土釘變形能和外力做功兩部分[25]組成，總平衡方程為

Π=U+W

(7)

式中：U為樁身應變能；W為外力做的功。

試驗節泡型土釘和節泡型土釘示意見圖6。土釘入土深度為L，土釘抗拔力為P；土釘桿的直徑為D1、長度為L1；土釘節泡的直徑D2、節泡弧面段的長度為L2-L1、節泡面段的長度為L3-L2；β為節泡弧面假設為線性與土釘桿的夾角；Q1、Q2、Q3和Q4分別是土釘桿摩阻力、沿著節泡弧面摩擦力、節泡弧面垂直壓力以及節泡面摩阻力；Sb、Sf、Sz和St分別是土釘端位移、節泡平面位移、節泡弧面位移以及土釘頂位移。為簡化推導做出如下假設：①土釘與土體都是具有各向同性、均質的材料；②土釘節泡面段假設為圓柱體，且節泡弧面段假設為圓臺；③土體的極限抗壓強度隨著注漿壓力的增加沒有變化。

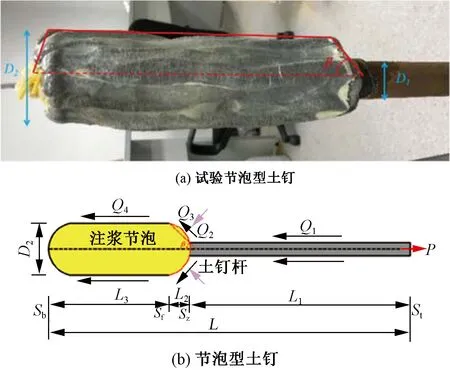
圖6 試驗節泡型土釘和節泡型土釘示意

節泡型土釘存在節泡，土釘的截面直徑存在變化，因此，將節泡型土釘進行差分分段分析，如圖 7所示，整個土釘的應變能為

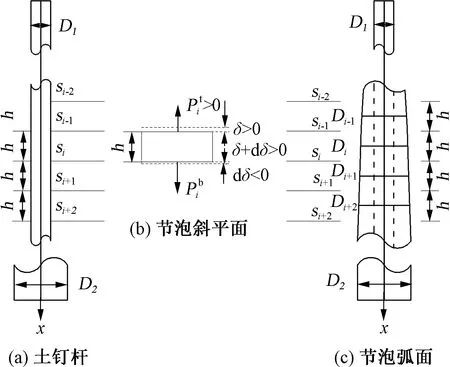
圖7 節泡型土釘差分圖

(8)

根據Cao等[26]半無限空間理論來分析壓密注漿土釘節泡弧面受力，如圖 8所示，土釘受到荷載P作用，土釘發生位移，將斜面的作用力分解成垂直斜面的壓力Q3與沿著斜面的摩擦力Q2，即沿著土釘斜面的摩擦力，外力做的功W表示為

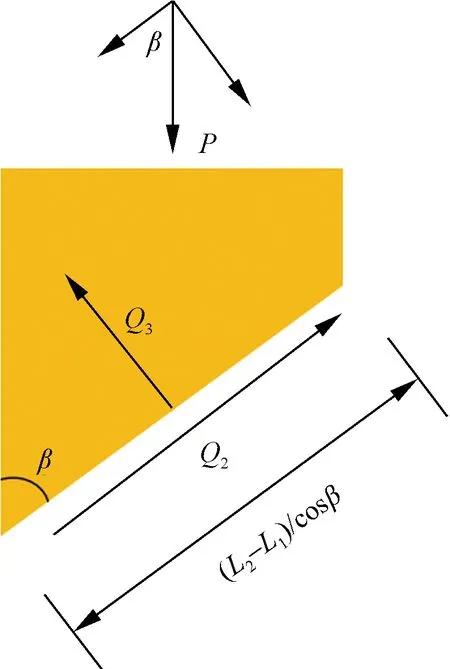
圖8 節泡弧面受力

W=Wf+WF+WP

(9)

Wf=-?τ(x)(δ+sb)ds

(10)

WF=-?Q3(sb+δ(L3-L1)/L)sinβds

(11)

WP=Pst

(12)

聯立(7)～(12)式可得

(13)

根據式(13)，得出土釘桿(當0≤x≤L1時)的能量平衡方程為

(14)

將式(14)通過待定系數法可得

(15)

(16)

根據式(13)可得，節泡弧面(當L1≤x≤L2時)的能量平衡方程為

(17)

同理將式(17)通過待定系數法得到

(18)

(19)

式中：ω=π(nh-L1)tanβ+πD1；n為計算段到土釘的差分個數。

根據式(13)同理得節泡平面(當L2≤x≤L3時)能量平衡方程為

(20)

同理，通過待定系數法可得

(21)

(22)

由于節泡型土釘的每一段都是連續的，將每一段的摩阻力與位移的關系式(1)～式(6)代入式(19),得到節泡型土釘的位移與抗拔力表達式為

(23)

聯立邊界條件，Pn+1=0與P1=P，即可求得節泡型土釘的抗拔力與抗拔位移的曲線。

2 試驗與驗證分析

2.1 試驗系統

本文試驗是在紐卡斯大學節泡型土釘室內試驗系統中完成，該試驗系統分為試驗模型箱裝置、拉拔加載裝置、上覆土壓力加載裝置、注漿裝置、數據采集裝置五個部分組成，見圖9。

圖9 室內模型試驗系統(單位：mm)

試驗模型箱裝置主體為1 000 mm×600 mm×800 mm(長×寬×高)的長方體。拉拔加載裝置由液壓千斤頂和位移傳感器(LVDT)等組成。上覆土壓力加載裝置由可變的壓縮空氣、橡膠袋、位移傳感器及閥門等組成。注漿裝置由注漿管、漿液筒、天平、可變的壓縮空氣及閥門等組成。漿液筒用儲存水灰比為0.5且密度為1.80 g/cm3的漿液，天平用來測漿液質量變化指標，可變的壓縮空氣擠壓漿液到乳膠膜中去，閥門是用來實時控制注漿壓力，防止注漿壓力過大對節泡造成破壞。數據采集裝置包括體積含水量傳感器(VWC)、土壓力傳感器(EP)、張力計、位移傳感器、數據采集儀以及計算機等組成。

2.2 試驗方案

本次模型試驗砂土為澳大利亞Stockton Beach Sand，其物理特性指標與級配特性見文獻[18]。本次模型試驗砂土試樣含水量為3%，干密度為1.48 g/cm3。試驗拉拔荷載通過液壓千斤頂以1 mm/min的速率對有無壓密效應兩組節泡型壓密注漿土釘進行拉拔。

2.3 試驗步驟

Step1裝樣：將制備好的土樣分層壓實，分層的厚度控制為40 mm左右，同時，在裝樣的過程中分別安裝好壓密注漿土釘及土壤物理參數傳感器[27]。在做無壓密效應的對照組時，把壓密效應的節泡土釘埋入相同的壓實度的土體中，從而控制有無壓密效應節泡體積大小相等。

Step2上覆土壓力設置：通過模型箱上部的上覆土壓力加載裝置設置上覆土壓力OP為100 kPa，模擬節泡型壓密注漿土釘的埋深處的上覆土壓力。

Step3注漿：調節可變的壓縮空氣對安裝土釘進行壓密注漿，注漿壓力GP分別為400、500、600、700、800 kPa。無壓密效應通過控制漿液的體積來與壓密效應進行對比組。

Step4加載：待水泥漿養護7 d后，利用液壓千斤頂對兩組土釘試驗(壓密效應和無壓密效應)進行1 mm/min的速率進行拉拔。同時，記錄好抗拔力隨抗拔位移的變化數據和節泡附近體積含水率的變化，從而通過換算得到干密度隨注漿壓力的變化關系。

本文理論方法與室內模型試驗結果進行對比驗證。本文計算方法的計算參數見表1，算例1是無壓密效應的理論計算方法參數，算例2為考慮壓密效應的理論計算方法參數，節泡直徑與注漿壓力的關系見文獻[18]。本文理論方法計算值與無/有壓密效應室內模型試驗值對比分別見圖10和圖1。

表1 驗證分析參數

圖10 無壓密效應抗拔力理論值與試驗值對比曲線

由圖 10可知，當注漿壓力GP≥600 kPa時，本文理論計算值的分布相較于試驗值偏低，當注漿壓力GP<600 kPa時，本文理論計算值的分布卻高于試驗值。圖 11給出不同注漿壓力下土釘抗拔力的試驗值與理論計算值，在位移小于50 mm時，本文的理論計算值小于試驗值，這是由于試驗過程中的節泡的形狀并不是規則的，導致試驗值在局部會與計算值有一定的出入，但是總體上與試驗值吻合的較好，驗證本文計算方法的合理性。

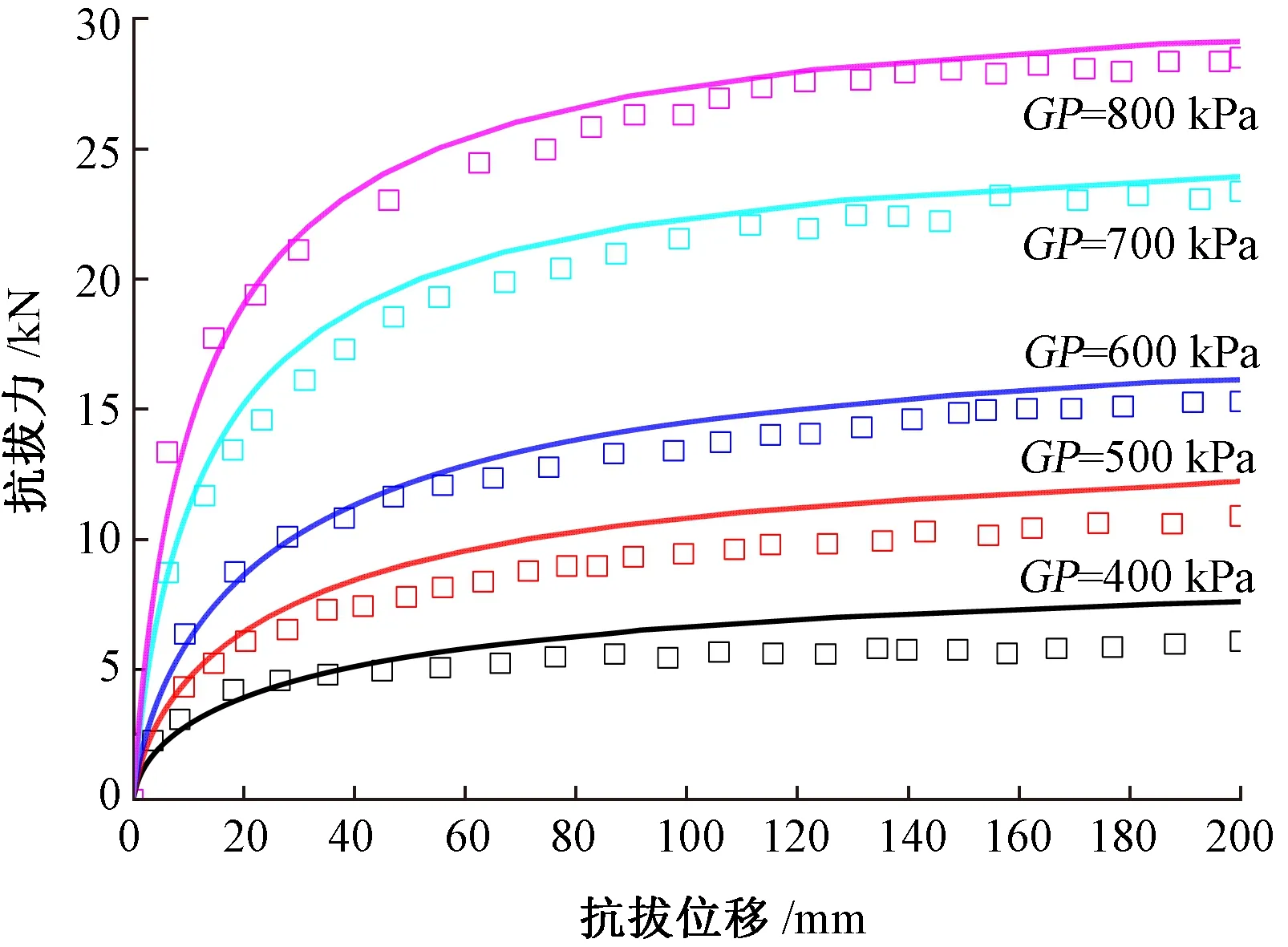
圖11 壓密效應抗拔力理論值與試驗值對比曲線

2.4 初始壓縮模量E0參數分析

本文通過改變初始壓縮模量與速率因子參數的算例來探討節泡型抗拔規律。參數取值與驗證分析的算例2的參數一致，無壓密效應的參數取值為算例1，為了與初始壓縮模量E0做對比，其初始壓縮模量E0為30 MPa，在考慮相關參數影響時再重新取值。

圖 12給出不同初始壓縮模量(E0=25、30、35、40、45 MPa)與無壓密效應下對節泡型土釘抗拔力的影響，在注漿壓力不變的情況下(GP=800 kPa)，初始壓縮模量E0對壓密注漿土釘極限抗拔力的效果很小，影響主要體現在發揮速率上，相比于無壓密效應，壓密效應提高節泡型土釘的抗拔力。通過歸一化抗拔力得出，隨著抗拔位移增加，初始壓縮模量E0的影響效果減小(從2.8降到1.2)，這是與本文所得到的試驗結果是一致的，壓密效應提高抗拔力的發揮速率。

圖12 不同初始壓縮模量E0對壓密注漿土釘抗拔力影響曲線

不同初始壓縮模量E0下節泡弧面摩阻力變化見圖13。由圖13可見，壓密注漿土釘抗拔力的來源主要是節泡弧面的摩阻力(占比達到90%)，初始壓縮模量E0可提高節泡弧面摩阻力的占比，這與文獻[18]得到的結果一致。通過在實際工程中壓實土體，提高初始壓縮模量，會提高節泡型土釘的抗拔力發揮的速率，而在實際工程中，抗拔位移不會過大，因而提高了節泡型土釘的抗拔性能。

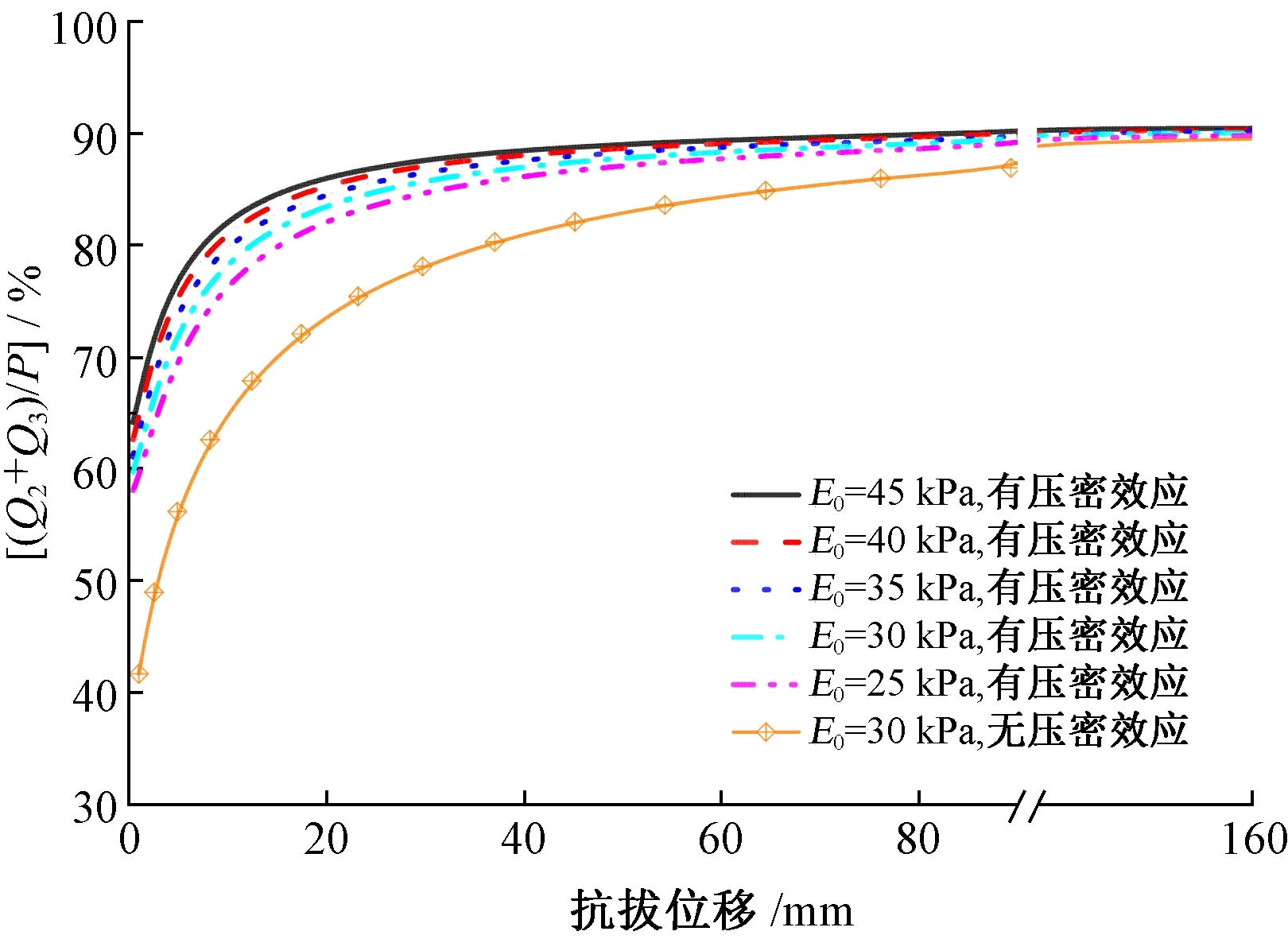
圖13 不同初始壓縮模量E0下節泡弧面摩阻力變化曲線

3 結論

(1)本文通過指數模型描述壓密效應的影響，并采用能量原理推導出考慮壓密效應的能量平衡方程，獲得節泡型壓密注漿土釘抗拔力與抗拔位移之間的計算方法，該方法也可退化為無壓密效應的土釘抗拔力計算。本文理論解與壓密效應和無壓密效應的室內模型試驗值吻合的好，驗證本文方法的合理性。

(2)參數分析表明，初始壓縮模量影響抗拔力的發揮速率，而對極限抗拔力(抗拔位移為200 mm)效果不明顯；節泡弧面的摩阻力是節泡型土釘抗拔力的主要來源。速率因子的增加不僅使土釘抗拔力的發揮速率降低，還會降低土釘的極限抗拔力，節泡弧面的摩阻力發揮在拉拔位移為50 mm之前也隨之減慢。本文針對砂土中的節泡型壓密注漿土釘的計算方法進行研究，對節泡型土釘在其他土體類型中的速率因子參數確定需進一步研究。