基于改進遺傳算法零件加工工序優化研究

郝博，傅士栗，王建新，王明陽，閆俊偉

(1.東北大學機械工程與自動化學院，遼寧沈陽 110819；2.東北大學航空動力裝備振動及控制教育部重點實驗室，遼寧沈陽 110819)

0 前言

在計算機輔助工藝過程設計(Computer Aided Process Planning，CAPP)解決的問題中，加工工序規劃是一個非常重要卻又復雜的部分，不僅加工方法、刀具、機床等加工資源的選擇會對工序規劃產生影響，而且工藝約束也會對工序的排序產生制約。僅僅使用傳統的方法，比如梯度下降法、圖論法和仿真方法實現路線優化，在解決復雜的零件工序規劃問題上效率很低，只能完成結構較簡單的零件或復雜零件的某一部分工序排序規劃的內容[1]。加工工序優化在某些重要領域，比如汽車制造、航空航天、裝備現代化生產等行業的大規模生產中起到了重要的作用[2]。近年來，智能算法作為主要研究手段被廣泛應用于工序規劃的研究中。鄭永前、鄭開元、曹振、黃偉軍等[3-6]采用遺傳算法，針對工序排序問題，以成本最低或最大完工時間最少為優化目標，完成對應編碼與解碼解決方案。劉偉等人[7]運用蟻群算法，以海明距離反映任意兩加工單位之間的相似程度，并在約束條件和禁忌準則的限制下對解空間進行搜索。劉敏等人[8]把模擬退火算法引入到傳統遺傳算法中，解決了加工中心的工步優化問題。姜存學等[9]將模擬退火算法與蟻群算法結合，建立零件工步優化過程模型，將之應用于以加工中心為主要加工設備的創成式CAPP中。但是，目前針對零件工序規劃問題所采用的遺傳算法存在一些不足：(1)沒有考慮到在實際車間生產中，對于某類加工特征，通常存在幾種加工方案，并且對于一個工步的加工，有多臺機器可供選擇；(2)現有算法采用間接編碼方式，對解的信息表達不直觀，解碼復雜度高，影響了算法的效率；(3)現有遺傳算法研究中對于種群的優化方法和進化導向使得算法的全局搜索能力不強，在運行過程中產生的新種群多樣性逐漸降低，易使搜索進入局部收斂甚至發生停滯。

針對上述不足，本文作者設計分層多算子遺傳算法(Hierarchical Multi -Operator Genetic Algorithm，HMO-GA)，其編碼分為特征層、工序層、機器層、刀具層、方向層以及選擇層，每一層對應工藝規劃的一個維度，使得染色體中包含的決策信息更加豐富且直觀，降低解碼難度，減少算法求解時間，提高效率。對于每一個搜索維度，針對性采用不同的遺傳優化算子，提高算法的全局和局部搜索性能，避免發生局部最優。采用面向加工資源使用的變異算子代替隨機變異算子，從而改善全局平衡，增加繁殖更好的個體概率；選擇層編碼設計對算法的性能有很大幫助，選擇層的基因突變使得特征加工方法選擇方案改變，實現柔性加工的靈活性。

1 相關概念和數學模型

1.1 工步信息表示

零件加工的單元為工步，工序排序就是將所有工步進行排列組合，而工步的選擇制定面向的是零件的加工特征。一般來說，復雜的零件加工特征基本可以由面(外圓柱面、圓錐面、平面)、凸臺、槽(環槽、方形槽、鍵槽、通槽)、肋、孔(普通孔、螺紋孔、沉頭孔、盲孔)等構成。在零件加工特征排序問題上把每一個加工特征稱為加工元。所有的加工元的集合就構成了零件的加工特征，通過工藝知識庫的查詢，為每一個特征選擇合適的加工方法。若一復雜零件由n個加工元構成，則零件特征可表示為集合：

F={f1,f2，…，fn}

(1)

其中：fi為該復雜零件的第i個加工元。同一個加工元，根據加工精度的需要以及車間加工資源的限制，可能存在多種加工手段。例如，對于外圓面的加工，有粗精車→半精車→磨削、粗車→半精車→粗磨等多種不同的加工方式。對于內孔的加工，有鉆→擴→鏜、鉆→擴→鉸等不同的加工方式。所以對于每一個加工元根據實際需求以及車間資源可能存在多種加工方法，即一個加工元由多條加工鏈構成：

fi={OL1,…,OLi,…,OLm}

(2)

式中：OLi為加工元fi的第i條加工鏈。加工鏈是由工步經過線性排列組合而成，分為單個工步或多個組合工步。加工鏈可以表示為

OLi={OP1,OP2,…,OPk}

(3)

式中：OPi表示為加工鏈OLi的第i個加工工步。

為對加工特征進行更詳細準確的描述，用基于工步的三維工步矩陣存儲特征信息。其中：a為工步編碼的維度，分別為加工序號、加工特征、加工方法、加工精度、可用機床集合、可用刀具集合以及進刀方向，包含工步的特征信息以及加工所用到的資源信息；c為零件加工各特征的總工步數；b為每一特征可能選取不同加工方法的工步表示，將同一特征加工精度相同的工步存放在三維工步矩陣的不同層。圖1所示為三維工步矩陣。

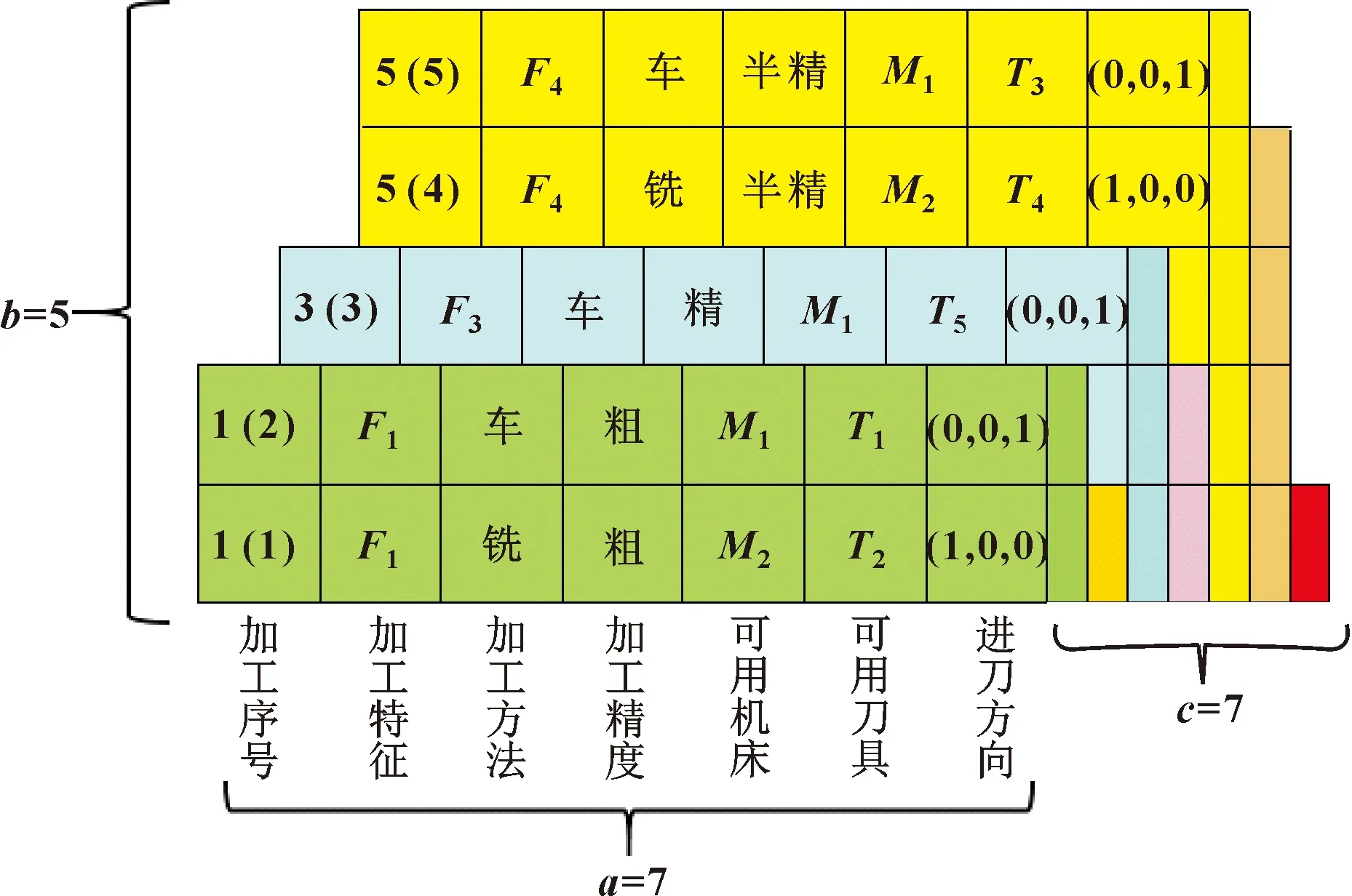
圖1 三維工步矩陣

1.2 工藝約束

將零件制造特征所選擇的加工工步集合進行排列組合，在不違反工藝約束的情況下，得到最優目標值的工步序列，這個計算尋優過程就叫加工工序優化。假設一個零件有N個待加工特征，從排列組合的角度來看，就會產生N！組工步序列，假設不存在其他的限制條件，則會存在N！個可行解[10]。由于加工零件特征具有具體的精度需求，并且要滿足設計的形位公差要求，所以加工順序的排列就不能是所有的可行解，必須要遵循在零件設計前提下加工工藝的限制。加工工序決策優化的前提是確保零件加工精度，使加工完畢的零件符合設計的標準，否則無用的工序排序對加工規劃而言毫無意義。所以，設計加工工序路線首先要滿足工藝的約束，包括以下幾個方面：

(1)幾何拓撲關系。即工件在加工過程中各特征的先后順序關系，如先面后孔，加工兩個相關聯的特征面和面上的孔時，工序排序必須滿足面在孔之前的約束。

(2)先基準后其他準則。作為加工基準的加工特征表面應該先于其他表面先加工，因為后續特征表面的加工需要以它作為定位基準保證精度。

(3)先主要后次要，先粗后精準則。精基準加工完畢之后再對精度有更高要求的表面進行加工，精度特別高的還需進行光整加工。主要表面的精加工放在最后階段進行，次要表面先進行加工或者穿插在主要表面加工工序之間。

通過對工藝約束的制定，結合具體零件的相關幾何參數和加工信息建立工步約束矩陣CS：

(4)

式中：CS為n×n矩陣；n表示所有工步個數；元素rij表示第i個工步和第j個工步之間的先后約束關系，定義規則如下：①根據工藝約束原則，若工步i在工步j之前加工，則rij=1，反之rij=-1；②若工步i和工步j相互之間沒有加工約束關系，則rij=0。

1.3 工序方案評價方法

加工工序優化的目標是在現有加工資源的條件下得到最優的加工方案，使得加工時間、消耗成本等目標值達到預期滿意的結果。工藝優化評價指標通常有最大完成時間、加工能量損耗、加工成本消耗等。文中用加工成本作為評價目標來對工序規劃過程進行優化，評價函數定義為

(5)

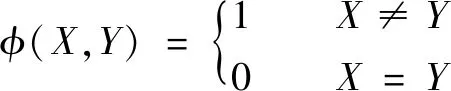
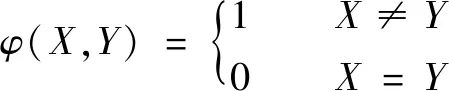
式中：α、β、γ、θ為權值系數；Mj為機床j單位時間內使用成本；Tk為刀具k單位時間內使用成本；Ti為加工第i個工步所耗費的時間；si為第i個工步的加工是否用到機床j，若si=1，則表示加工過程用到機床j,反之則沒有；ti為第i個工步的加工是否用到刀具k，若ti=1，則表示加工過程用到刀具k，反之則沒有；Ai(n)為加工鏈A的第i個工序的第n位編碼內容；Cmc為更換機床成本；Ctc為更換刀具成本；φ(X,Y)為工序X和Y之間是否更換機床；φ(X,Y)為工序X和Y之間是否更換刀具。

2 分層多算子遺傳算法

2.1 編碼與解碼

遺傳算法的編碼和解碼方法很大程度上決定了算法的可行性和效率，是解決問題的關鍵，也是實現算法計算機編程的必要條件。之前用遺傳算法解決工序規劃問題的研究多采用雙重編碼的方法，單個加工特征獨立編碼，每個基因包含多項加工內容，存在染色體表示不直觀、解碼復雜度高、效率低、局部搜索能力差等問題。為解決遺傳算法在工序排序問題上的不足，提出分層多算子遺傳算法。用多層編碼的方式映射6個獨立的決策層，分別是特征層、工序層、機器層、刀具層，方向層以及選擇層，它們之間相互關聯，共同影響著目標函數。

圖2所示為分層多算子遺傳算法染色體編碼實例。第一層為特征層編碼，實數表示特征編號，其相對位置反映加工順序的優先級關系，同一數字重復次數表示該特征加工工序數量。第二層為工序層編碼，其數字與后面幾層一一對應，位置反映了加工特征工步之間的先后順序關系。機器層和刀具層中顯示的數字代表在車間中對應可選工步的加工資源。加工方向層表示刀具的進給方向，結合具體實例，根據需要，設定初始方向和各進刀方向。第六層為選擇層，用于選擇零件各特征采用的加工方法，即加工鏈的構成，體現在工序的選擇上。所有染色體通過選擇層實現了特征的加工方案，數字1表示該工序被采用，否則未被采用。

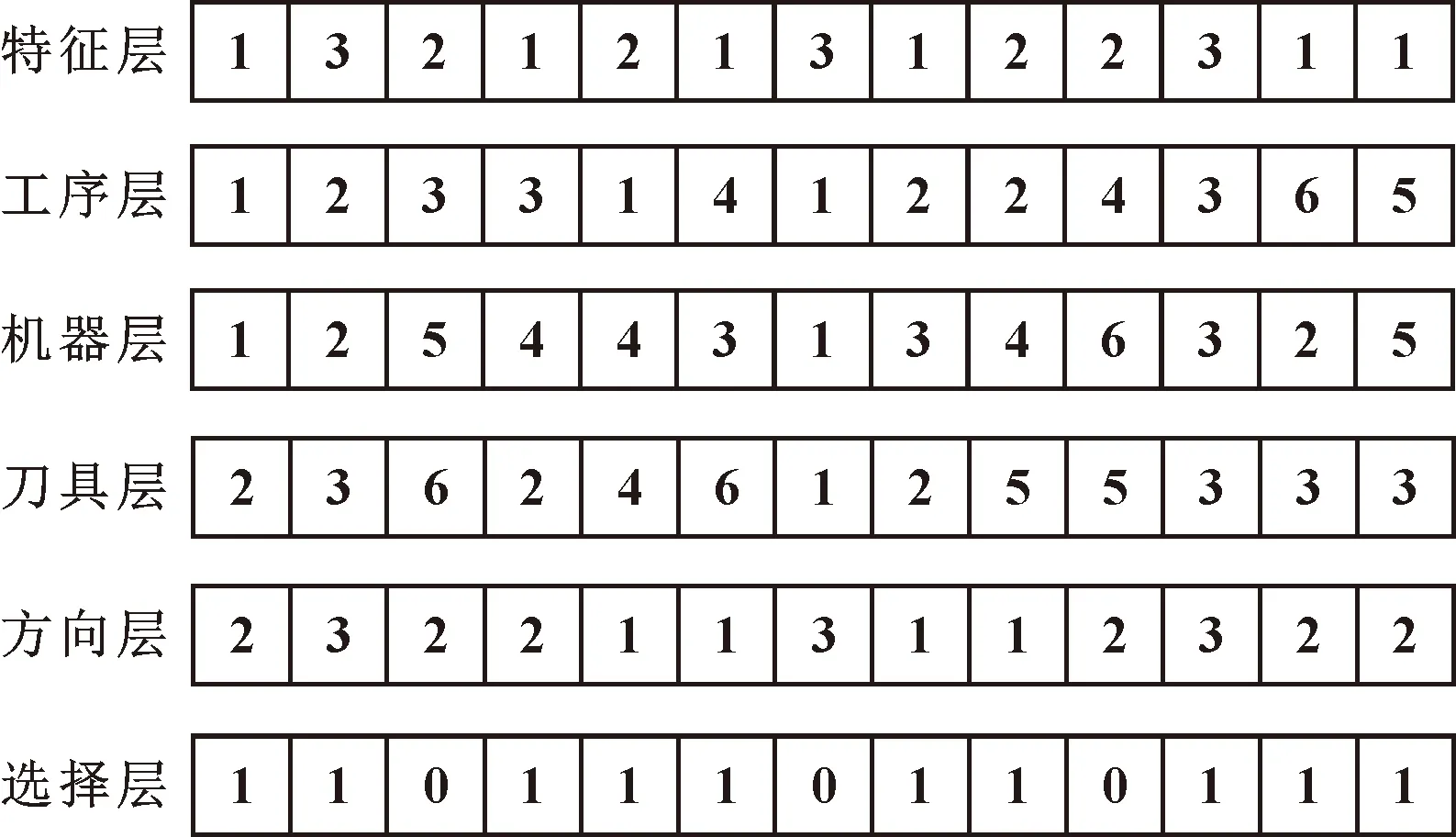
圖2 分層多算子遺傳算法編碼示例

分層多算子遺傳算法的解碼方式相對簡便。首先，將特征層、工序層、機器層、刀具層以及方向層中的數字以前五層的編碼順序和指定形式全部列出。隨后，將選擇層中編碼為0的基因列刪除。圖2所示的零件加工工序排序方案解碼輸出結果為

F1(OP1,M1,T2,TAD2)→F3(OP2,M2,T3,TAD3)→F1(OP3,M4,T2,TAD2)

→F2(OP1,M4,T4,TAD1)→F1(OP4,M3,T6,TAD1)→F1(OP2,M3,T2,TAD1)

→F2(OP2,M4,T5,TAD1)→F2(OP4,M6,T5,TAD2)→F3(OP3,M3,T3,TAD3)

→F1(OP6,M2,T3,TAD2)→F1(OP5,M5,T3,TAD2)

2.2 交叉與變異算子

2.2.1 交叉算子

交叉算子是產生新個體的主要方式，在很大程度上決定了智能算法性能的優劣。在交叉操作中，染色體的每一列都是作為位置轉換的基本單元。當一列中的任何基因位置改變時，該列中的所有基因都以相同的方式改變它們的位置。對特征層、工序層、機器層(刀具層、方向層)分別采用不同交叉算子，從多個維度進行迭代搜索，具體操作如下：

(1)對于特征層編碼交叉采用POX算子，該算子可以保證所有特征在父代和子代出現的次數一致，并保持任意特征工序之間的順序約束關系。特征層POX編碼交叉操作示例如圖3所示，具體步驟為

步驟1，從一個種群中隨機選擇兩條染色體，提取其特征層作為父染色體P1和P2,并初始化生成兩條空染色體O1和O2作為子代；

步驟2，將特征集合F劃分為兩個非空集合F1和F2,并滿足F1∪F2=F、F1∩F2=?；

步驟3，將P1中屬于集合F1的特征對應的基因復制到O1相同的基因位置，然后在P2中刪除O1中已確定的基因并將余下的基因從左到右依次填充到C1的空基因位置上；

步驟4，把P1、P2位置互換，再按照步驟3中同樣操作步驟得到C2。

圖3 特征層POX交叉示意

(2)對于工序層采用兩點交叉算子，保證在交叉完成后生成的子染色體工序層序列的完整，避免重復或者遺漏，符合實際。該算子為局部操作，作用在兩條隨機染色體對應同一特征的工序層基因之間，如圖4所示，具體操作過程如下：

步驟1，從種群中隨機選取兩條染色體作為交叉操作的父染色體，記為P1和P2。分別提取兩條染色體的工序層基因，記為PP1和PP2，生成一條空的工序層基因作為子代，記為OP1；

步驟2，標記選擇層代碼為1的工序操作；

步驟3，隨機選取兩個交叉點位置，從左到右分別記為Pos1和Pos2；

步驟4，將PP1中Pos1左側基因和Pos2右側基因按照對應的位置復制到OP1兩側；

步驟5，在PP2篩選出不含PP1已復制到OP1中的基因，逐一插入到OP1中空缺位置；

步驟6，根據步驟1的記錄調整OP1中選擇層的編碼，使選擇層OP1編碼為1的基因與PP1相同；

步驟7，將得到的OP1基因插入到染色體P1中PP1的原始位置，獲得新的子代染色體。

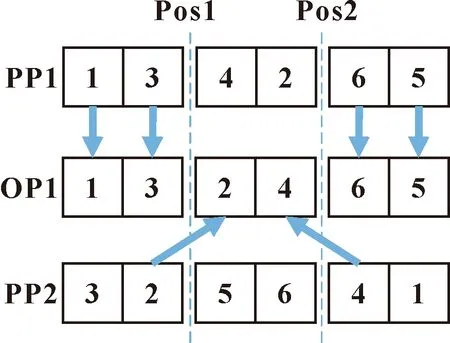
圖4 工序層兩點交叉示例

(3)對于機器層、刀具層以及方向層均采用類似子圖交換的交叉操作。如圖5所示，將機器層交叉作為示例，隨機選擇兩條父代染色體用作交叉操作。具體步驟如下:

步驟1，從種群中隨機選取兩條染色體作為父代染色體，分別提取同一特征對應的工序層和機器層基因，記為PM1和PM2，生成空基因層OM1；

步驟2，將PP1的工序層復制給OM1；

步驟3，隨機產生特征工序層的n個位置用作交叉，將PM1機器層對應n位置的基因復制給OM1，將PP2對應剩下OM1中工序編號的機器層編號復制到OM1中；

步驟4，將OM1插入到PM1基因原位置的父染色體P1中，獲得新的子代染色體。

圖5 機器層兩點交叉示例

2.2.2 變異算子

設計從多個維度對染色體進行變異，針對每個維度選擇不同的變異算子。特征層變異，改變不同特征的加工先后次序；工序層變異，改變同一特征的加工工序次序；機器層(刀具層、方向層)變異，使作業加工資源發生變化；選擇層變異，改變特征采取的加工方式。與交叉操作一樣，染色體的每一列都是變異操作中位置轉換的基本單元。

(1)特征層的變異，采用如圖6示例所示的方法,具體步驟如下:

步驟1，在染色體P中隨機選擇兩個位置Pos1和Pos2,如果兩個位置的編碼所代表的特征相同，則重新選擇兩個位置，直到編碼號不同，并記錄為P1和P2；

步驟2，分別在Pos1和Pos2之間的染色體片段中標記P1和P2的所有基因位置；

步驟3，用第一個P2基因列覆蓋第一個P1基因列，然后將片段中剩余的P2基因列向左移動，并逐個填充空缺，將Pos2位置留空；

步驟4，將P1最右邊的基因列填充到Pos2的位置，然后將P1剩余的基因列向右移動，依次填充空缺，得到特征層突變后的個體O。

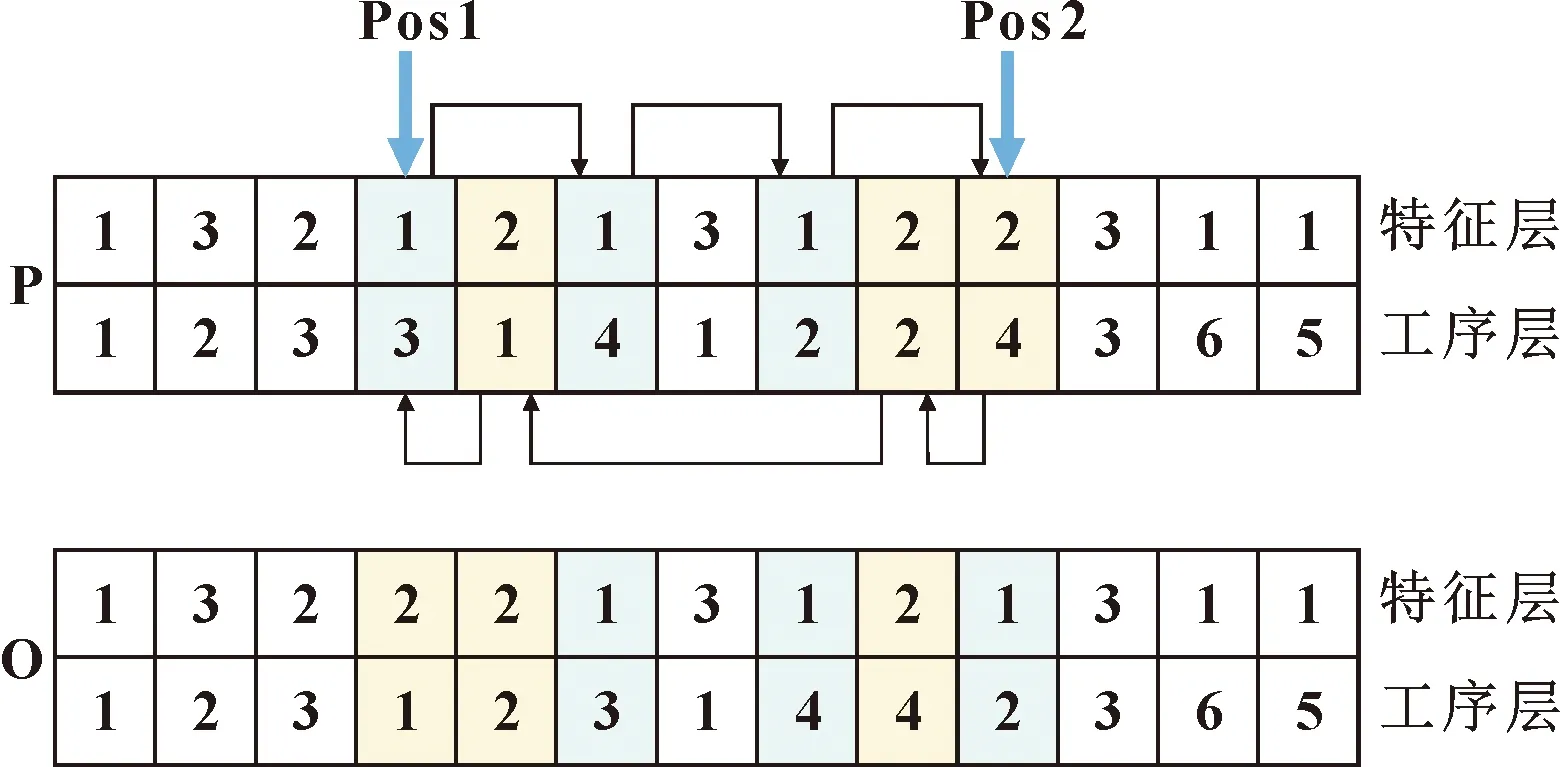
圖6 特征層變異示例

(2)工序層變異，采用位置互換的方法，如圖7所示,具體步驟如下:

步驟1，隨機選擇一個染色體進行突變，標記為PO；

步驟2，提取PO的工序層基因，標記其基因位置；

步驟3，在染色體中隨機選擇兩個位置，將兩個位置處的基因進行交換作為突變；

步驟4，確定變異后的工序序列是否滿足約束矩陣的要求；

步驟5，若滿足約束要求，則將其插入到PO染色體原位置,否則，使用約束矩陣對序列進行調整，再插入到PO中。

圖7 工序層變異示例

(3)機器層、刀具層、方向層的變異均采用單點突變的方式。以機器層為例，對機器利用頻率最高的基因實施變異。圖8所示為機器層變異示例,具體步驟如下:

步驟1，計算機器利用率,機器利用率等于機器加工時間除以完工時間

步驟2，提取利用率最高的機器Mi在編碼中的所用位置，并記錄下來；

步驟3，隨機選取步驟2中記錄位置所含編碼基因進行突變。

圖8 機器層變異示例

(4)選擇層的變異，采用多點變異的方式。隨機選擇一條染色體，提取一個特征的選擇層進行變異。選擇層變異如圖9所示，具體步驟如下：

步驟1，隨機選擇一個特征進行基因突變，記為F；

步驟2，提取F中選擇層的基因，并標記其位置；

步驟3，在特征F的可選加工方案中選擇與當前方案不同的加工鏈；

步驟4，根據選擇的加工鏈中包含的工步信息生成新的選擇層代碼；

步驟5，將步驟4得到的選擇層基因替代F中原位置處的基因，生成新個體。

圖9 選擇層變異示例

2.3 改進遺傳算法實現步驟

傳統的工序規劃遺傳算法編碼復雜，增加了解碼的難度和時間。搜索算子的設置比較單一，導致算法在搜尋最優解的能力方面不足。本文作者對遺傳算法進行改進，提出分層多算子遺傳算法，提高了工序排序問題的全局搜索能力，將工序選擇靈活性、工序排序靈活性、加工資源選擇靈活性集成到單個階段。具體步驟如下：

(1)根據工藝約束矩陣的約束，使種群中包含的個體加工順序成為有效解；

(2)計算種群的個體適應度函數值，并根據所計算出來的適應度大小對它們進行排序；

(3)將種群中的染色體作為父代隨機進行交叉和變異操作；

(4)根據各層的交叉概率，依次對選定的父個體進行特征層、工序層、機器層、刀具層以及方向層交叉，生成新個體；

(5)根據各層的變異概率，對新個體依次進行特征層、工序層、機器層、刀具層、方向層以及邏輯層變異，生成新個體形成后代種群；

(6)對新形成的種群中個體的適應度進行計算，并將其與父代染色體中優秀的個體結合，形成新的種群；

(7)判斷結果是否滿足算法終止條件。如果是，輸出計算結果；如果沒有，返回步驟(3)。

3 實例驗證

為驗證改進算法的有效性，選擇如圖10所示的箱體零件進行驗證。該零件共有16個制造特征，加工這些特征共需要26個工步。關于零件加工的相關消息如表1—表3所示。

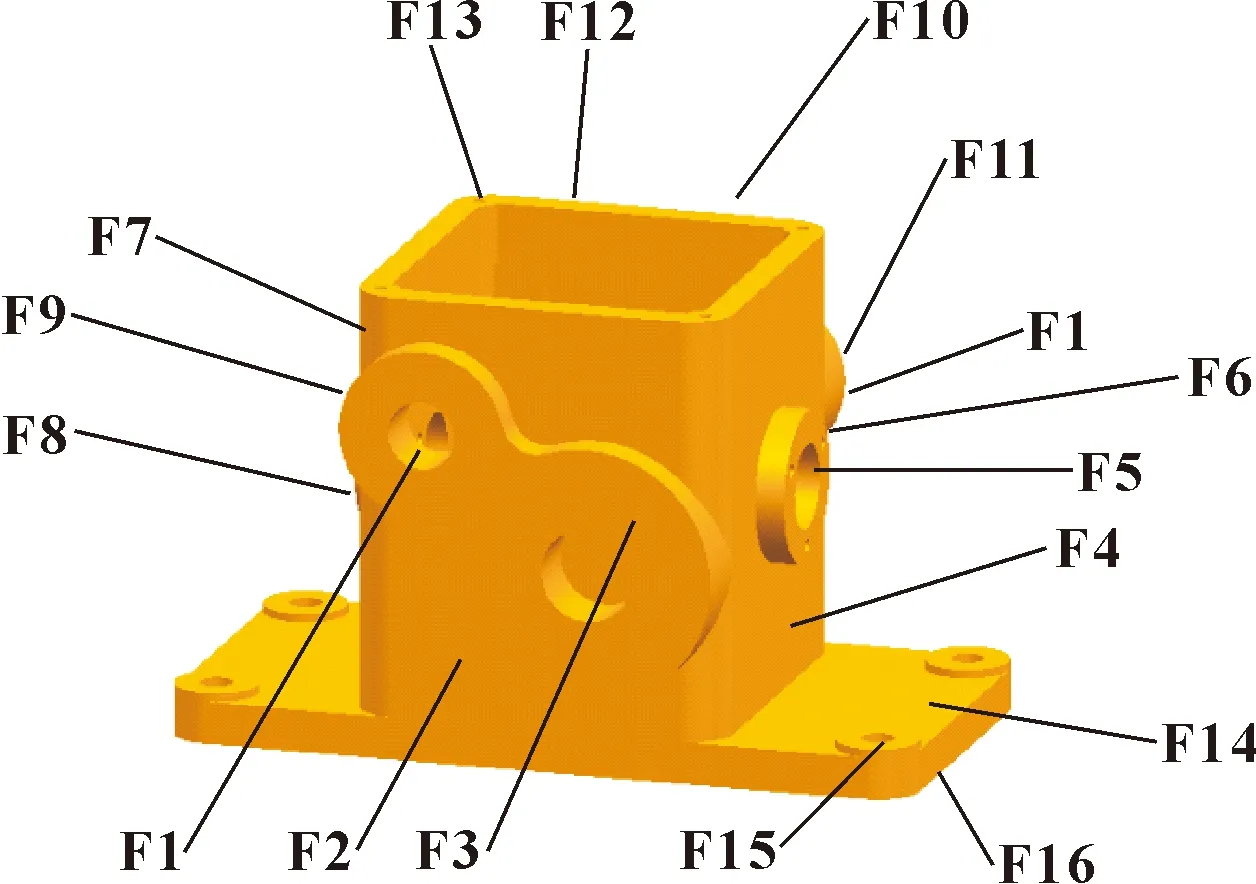
圖10 某箱體零件

表1 機床使用成本 單元:元·h-1

表2 刀具使用成本 單位:元·h-1

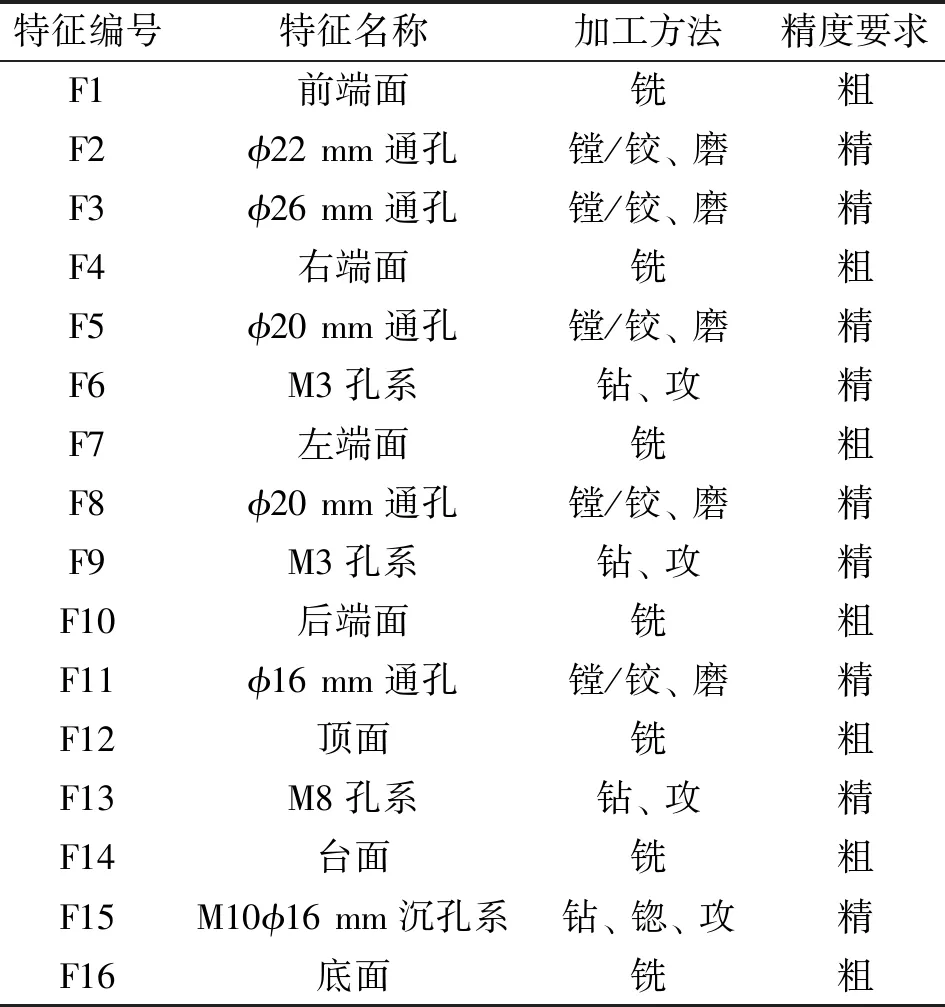
表3 零件特征及加工信息

根據零件加工特征和加工方法以及制造資源之間的拓撲關系，可以得到工步三維矩陣。由于工步三維矩陣的平面可視化較為困難，用表4對其進行描述。

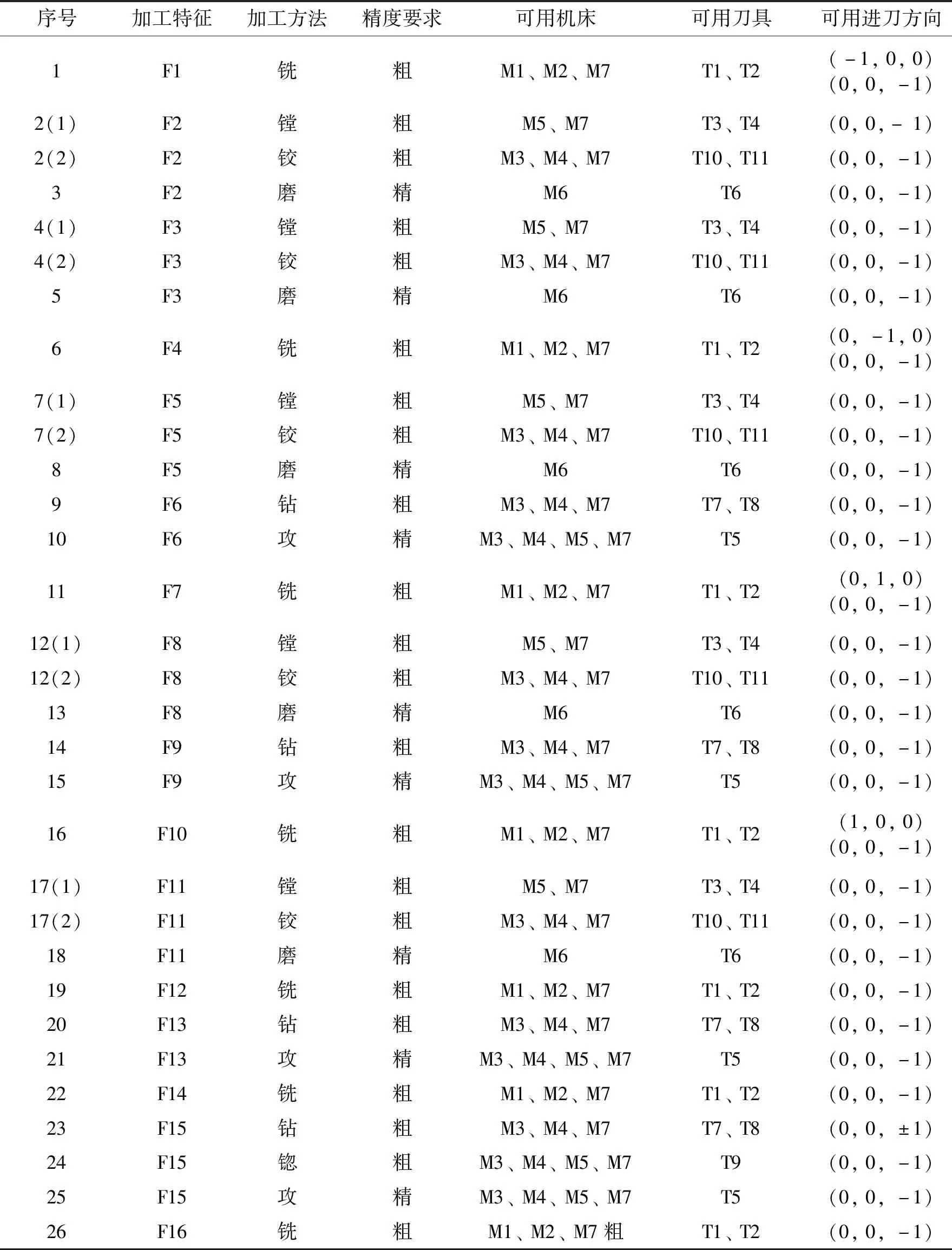
表4 工步三維矩陣

表4中的列對應工步三維矩陣列表示內容，序號表示元素在矩陣中的行數，括號內的數表示層數，即可選的加工方法。

用MATLAB完成分層多算子遺傳算法編寫。設置初始種群規模大小為M=100、交叉概率Pc=0.8、變異概率Pm=0.2、最大迭代次數為100。通過算法進行求解，得到如下結果：總成本為5 621.3元，機床更換了10次，刀具更換了11次，裝夾方式更換了11次，得到最優加工工序規劃為26→22→16→1→6→23→24→4(1)→2(2)→17(1)→11→18→12(1)→13→14→15→3→25→19→20→7→8→9→10→21→5。

為驗證文中算法的有效性，將傳統遺傳算法、文獻[5]中的遺傳算法應用于該箱體示例作為比較，迭代過程如圖11所示。可知：通過分層編碼的方法，大大降低了解碼的復雜度，提高了算法的效率；引入多種交叉、變異算子，提高了算法的全局搜索能力，加快了收斂速度。

圖11 改進遺傳算法迭代過程

4 結論

本文作者完善了評價函數模型，考慮到了在加工過程中因特征可選擇的加工資源不同而導致的成本差異。在改進的算法中添加選擇層，以動態的多加工鏈特征加工方法代替了傳統的靜態單一加工鏈，增加了加工過程中工藝路線的柔性。設計了分層多算子遺傳算法，用分層的實數編碼代替了雙重編碼，降低了算法解碼的復雜度，減少了算法求解時間，使得效率大大提升。針對算法的不同維度引入有效的交叉、變異算子，全局搜索能力提升，從而高效地對最優的工序排序進行快速搜索。

將箱體零件作為實例對算法的有效性進行驗證，結果表明：該算法在搜索結果和搜索效率上都有了明顯提高；在工序排序問題上與傳統的遺傳算法和模擬退火遺傳算法相比，該算法有更好的尋優性能。