基于改進BAS-BPNN的Stewart平臺位姿正解

王淑良，朱 浩，趙明偉,2，劉麗俊,2

(1.江蘇師范大學電氣工程及自動化學院，江蘇徐州 221116； 2.上海大學機電工程與自動化學院，上海 200444)

Stewart平臺屬于六自由度并聯機構，主要由上平臺、下平臺以及6個可伸縮的驅動桿組成，從機構學的角度講，并聯機構具有高剛度，并具有精確的定位能力，其高水平并聯設計產生了優于串聯機構的負載能力、動態性能和定位精度[1]。并聯機構已在飛行模擬器以及各種駕駛模擬器、新型機床、航空航天對接等領域得到了廣泛應用[2-4]。

Stewart并聯機構運動學正解需要求解一組強耦合非線性方程組，目前缺乏求解運動學方程的有效算法[5]。傳統的正解方法分為數值法和解析法：數值法核心為迭代計算，一般以Newton法為基礎，通用性好，求解穩定精度高，但是其為局部收斂，對初始值敏感，初值選取不當容易出現不收斂[6];解析法通過建立約束方程、消元和幾何分析等方法建立了幾種特定結構并聯平臺的封閉解，雖可以求得機構全部運動學正解，但是計算過程極為復雜，缺乏通用性[7]。為了解決Newton-Raphson對初始值敏感性的問題，很多學者提出了解決方案，WANG等[8]采用自然坐標的方法得到一組二次方程的Stewart平臺的運動學模型，利用此特性簡化了Newton-Raphson算法，以減少方程和雅可比矩陣之間迭代的更新時間；謝志江等[9]提出了基于最速下降法和多元牛頓法的組合數值方法，在降低對初始值依賴的同時還減少了單步迭代的計算量乃至更快速的收斂。

近年來，學者們開始借鑒智能算法解決位置正解問題，以此彌補傳統運動學正解算法的缺陷。很多研究者采用遺傳算法[10]、模擬退火算法[11]、人群搜索算法[12]等來求解位姿正解，取得了一定的成果。BP神經網絡對非線性映射有非常好的逼近能力，無需推導輸入、輸出的顯性表達式并且運算效率高[13]，但是單一的BP神經網絡容易陷入局部最優，很難滿足平臺正解的精確要求。眾多學者基于該算法進行了改進。李晶[14]采用遺傳算法(GA)優化RBF神經網絡模型，驗證了遺傳神經網絡正解法具有較好的收斂性和較快的速度，能夠滿足Stewart平臺運動學求解的需要；LI等[15]采用全局搜索能力更好的粒子群算法(PSO)對BP神經網絡模型進行學習訓練，訓練時間更短，求解精度更高，易于實現Stewart平臺的實時控制。與GA和PSO不同，天牛須搜索算法(BAS)是單體搜索算法，能夠大大減少運算量和時間[16]。

本文基于BAS具有一定的精度和快速的尋優能力，對BAS的步長調整和引入慣性權重進行改進，驗證改進后的BAS優化BP神經網絡模型對求解Stewart平臺正解具有高精度和運算速度的優越性，以解決平臺正解需要的準確性和實時性問題。

1 運動學反解模型

本文研究的Stewart平臺的上、下平臺通過虎克鉸與電動缸的兩端相連，通過6個電動缸的協調運動，可以實現3個方向的位置移動和姿態轉動。運動學反解是通過并聯平臺的位置和姿態，求各個電動缸長度的過程。定義平臺坐標系，以上平臺中心O1和下平臺中心O分別建立動、靜坐標系，上平臺的位姿由動坐標系相對于靜坐標系的廣義坐標表示，位姿由6個參數x,y,z,α,β,γ表示，x,y,z分別表示上平臺沿X，Y，Z軸移動的平移量，α,β,γ分別為橫滾角、縱擺角、偏航角，表示上平臺繞X，Y，Z軸旋轉的角度。

采用n+1維向量來描述n維向量再進行坐標變化，如空間坐標系中某點P通過四維向量(xp,yp,zp,1)表示，平移變化矩陣為Tp，繞三軸旋轉變化的矩陣為Tx,Ty,Tz，動坐標相對于靜坐標系的旋轉變換矩陣T=TxTyTzTp表示為

(1)

式中：cα=cosα；sα=sinα。

Stewart平臺的上平臺鉸點為P1-6,下平臺鉸點為B1-6，上平臺半徑為Ra,下平臺半徑為Rb，上平臺鉸點夾角為2a,下平臺鉸點夾角為2b，平臺的主視圖和俯視圖分別如圖1 a)和圖1 b)所示。

圖1 平臺示意圖

根據平臺的空間向量關系可以得到：

li=Pi+H-Bi，

(2)

式中：Pi，Bi，li分別表示靜坐標系中上平臺中心點到第i個上鉸點的向量，下平臺中心點到第i個下鉸點的向量和第i個電動缸的空間向量，則上平臺在初始中位時各缸的長度為|li|。當上平臺運動到目標位姿時，即動平臺進行平移旋轉運動，圖2是位姿變化示意圖，空間向量關系為

li′=TPi+H-Bi，

(3)

式中TPi的結果采用3維向量表示，則變化后的各電動缸的長度為|li′|。

2 IBAS-BPNN模型的建立

2.1 BP神經網絡

BP神經網絡是一種反向傳播網絡，具有良好的函數映射能力和數據預測能力，BP神經網絡通過對大量數據的訓練模擬出輸入數據與輸出數據之間的非線性關系[17]。結構上分為輸入層、隱藏層和輸出層，在隱藏層和輸出層中的每個神經元其凈激活量為

(4)

式中：netj是指此層中第j個神經元的凈激活量；xi是指神經元的輸入值；ωij，θ分別表示神經元上的權值和閾值。

初始化網絡的權值和閾值，對輸入的參數進行正向傳播，通過梯度下降法進行誤差反向學習，每次迭代都對權值和閾值進行調整，以訓練數據的均方誤差為目標，通過迭代學習，保證誤差與設定值接近后停止訓練。Stewart平臺有6根作動器和6個位姿參數，所以建立的BP神經網絡模型有6個輸入和6個輸出，輸入是作動器的長度，輸出是平臺的位姿參數。隱藏層的神經元個數參考經驗公式(5)，根據逐步增長或逐步修剪法反復實驗來找到最合適的值[18]，本文選取Q=20。同時，隱藏層選擇tansig函數作為激活函數，輸出層則選擇purelin函數，訓練函數選擇trainlm函數。

(5)

式中：I，O分別為輸入和輸出節點個數；C為常數。

2.2 天牛須搜索算法

天牛須搜索算法(BAS)是在2017年提出的一種生物啟發式智能優化算法，是受到自然界中天牛覓食原理的啟發[19]。天牛須搜索算法是單體智能尋優算法，具有個體簡單、計算量小、收斂速度快、全局優化能力強并且容易實現等優點[20]。在覓食過程中，天牛會通過2只觸角對空間的食物氣味進行感知，并且2只觸角距食物的遠近不同，所感知的食物氣味濃度也有差別，天牛會向著濃度強的一側隨機前進，最終找到食物的位置。BAS算法中天牛的當前位置即為所求解問題的一個可行解，食物的氣味濃度即為適應度函數。BAS算法的主要步驟如下。

Step1：設定2須之間的距離d0，步長為step，假設天牛的初始空間坐標為

X0=(x1,x2,...,xk)。

(6)

Step2：產生一個隨機向量b=rand(k,1)，并對其作歸一化處理，則創建天牛左右須的空間坐標：

(7)

Step3：更新天牛下一步位置：

Xt+1=Xt-δtb×sign[f(Xl)-f(Xr)]，

(8)

式中：f(X)是適應度值；sign()是符號函數；δt是第t次迭代時的步長。初始步長更新公式為

δt=eta×δt-1，

(9)

式中eta為步長因子，取值在0～1之間，一般取0.95，其作用是按比例減小步長，提高算法的收斂速度和性能。

2.3 改進天牛須搜索算法

BAS算法是一種不改變優化對象的隨機優化方法，當計算成本增加時，搜索算法的實時性能將降低。因此，合理的參數初始化和更新策略可以在一定程度上提高搜索效率[20]。KOU等[21]受到WCA隨機游蕩行為的啟發在左右觸角上添加了“隨機天線”，增強了局部搜索能力。

BAS算法的搜索能力和收斂速度受步長影響較大，原算法的步長策略容易過早收斂陷入局部最優，影響搜索效率和精度。本文對其步長策略進行改進，改進后的步長變化公式為

(10)

式中：δstart是天牛初始步長；δend是結束迭代時的步長；T是最大迭代次數。

通過式(10)可以看出，步長與迭代次數成負相關并且步長呈非線性減小，因此在迭代初期步長值較大且變化緩慢，有利于迭代初期找到滿足條件的局部最優值，并以較快的速度遍布整個搜索空間從而確定最優值的大概范圍；當接近最大迭代次數時，步長變化較快且接近迭代結束時的步長，由于此時天牛的搜索空間集中在最優值的附近，快速減小的步長能夠快速收斂逼近全局最優值。

一般來說，單體搜索的能力弱于群體搜索，在單體層次上可以通過引入慣性權重Wt，增強個體的搜索能力。這一原理與添加隨機天線類似，差別是慣性權重變化規律是通過人為設定的，前期較大的慣性權重值可以加快天牛對新區域的搜索速度，后期較小的權重可以增強天牛的局部搜索能力。權重更新的表達式和改進后天牛位置更新的表達式如下：

(11)

Xt+1=WtXt-δtb×sign[f(Xl)-f(Xr)]。

(12)

2.4 IBAS-BPNN模型建立

BP神經網絡的初始權值和閾值一般是通過隨機初始化的方式取得的，容易陷入局部最優。研究表明，使用優化算法對初始權值和閾值進行優化，很大程度上提高了BP神經網絡的性能[22]。利用改進天牛須搜索算法(IBAS)的優點，可以快速搜索出網絡的最佳初始權、閾值，以提高網絡全局最優能力。

Stewart平臺的6個電動缸的長度作為輸入數據集，平臺位姿的6個參數為輸出數據，隱藏層有20個神經元，IBAS優化的權、閾值總數為266個，權、閾值的合集即為天牛的位置。模型采用均方誤差(MSE)作為適應度評價函數來評估模型的準確性，通過迭代更新天牛位置得到最佳適應度值。IBAS-BPNN模型的結構如圖3所示。

圖3 IBAS-BPNN模型結構圖

3 仿真結果分析

以下結果都是在Intel Core i5處理器、8G內存、64位Windows 10操作系統、MATLAB 2019a的環境下仿真得出的。

平臺參數如表1所示。在平臺工作空間中隨機選取1 000組位姿進行反解計算得到對應的電動缸長度參數，將數據作為神經網絡的訓練集，在工作空間中選取1組變化的位姿作為測試集，通過測試集誤差性能驗證IBAS-BPNN正解法的適用性；選擇GA-BPNN，PSO-BPNN，BAS-BPNN模型與改進方法進行對比，并且采用MSE，RMSE和MAPE作為誤差性能指標進行評價，驗證IBAS-BPNN的優越性。

表1 平臺參數

3.1 IBAS-BPNN正解結果分析

在改進BAS-BPNN模型中，算法的參數設定通過反復實驗確定如下：初始步長δstart為5，結束步長δend為2，2須之間的距離d0為2，最大慣性權重Wmax為2，最小慣性權重Wmin為1/2，迭代次數為100。采用均方差作為模型迭代時的適應度值，圖4是IBAS-BPNN模型的最佳適應度曲線。由圖4可知，在迭代接近100次時，適應度值仍然發生變化，因此，本文嘗試迭代了200次，結果發現適應度值并沒有很大的提升，最終為了減少運算時間，綜合考慮后仍采用100次迭代為佳。

圖4 最佳適應度曲線

在平臺的運動范圍內選取一段位姿變化作為模型的測試數據，式(13)為選取的100組位姿數據點：

(13)

圖5是這段給定位姿通過模型正解的空間位置跟蹤情況，由圖5可以發現該模型的正解數據能夠跟蹤到給定位置。但是圖5無法反映平臺的空間姿態，因此將6個位姿參數分為了3個位置參數和3個姿態參數，圖6和圖7分別是測試數據的位置誤差和姿態誤差。由圖6可以發現，測試數據中最大位置誤差僅約0.12 cm；由圖7可以看出，最大姿態誤差不超過0.32°。由于選取的位姿在變化到參數接近給定的極限狀態時，位姿誤差通常比較大，因此引入誤差百分比這個指標來補充判斷正解精度水平。圖8是模型的誤差百分比，模型的最大誤差百分比不超過0.6%，并且較大誤差百分比都出現在位姿參數接近于0時。由于實際位姿參數作為分母較小會導致誤差百分比偏大，這也是在選取測試數據時舍去了t=0時位姿數據的原因。綜上所述，IBAS-BPNN作為Stewart平臺的正解方法在精度方面是滿足需求的。

圖5 空間位置跟蹤

圖6 位置誤差

圖7 姿態誤差

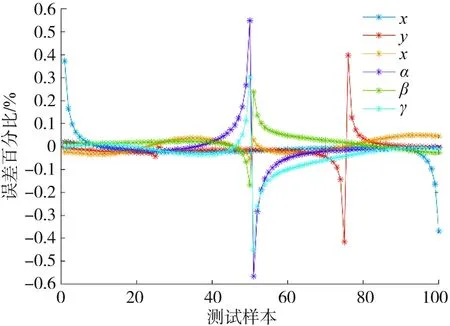
圖8 誤差百分比

3.2 模型性能指標對比

為了驗證IBAS-BPNN正解方法的優越性，本文在相同數據集訓練，并且迭代進化次數都為100的情況下，對比了GA-BPNN，PSO-BPNN，BAS-BPNN和IBAS-BPNN模型的誤差性能指標和運算時間，見表2。

表2 模型的誤差性能指標及運算時間

由表2可知，GA-BPNN的均方誤差(MSE)、均方根偏差(RMSE)和平均絕對百分比誤差(MAPE)都大于另外3個模型，PSO-BPNN的3個誤差性能指標優于BAS-BPNN但是運算時間遠大于BAS-BPNN，而IBAS-BPNN的誤差性能指標相比于PSO-BPNN略有優勢，并且運算時間僅需31.9 s，相較于改進前也有提升。GA-BPNN的正解精度最差且運算時間最長，IBAS-BPNN的正解精度最高且速度最快，而PSO-BPNN和BAS-BPNN在正解精度和運算速度上各有優勢。

綜上所述，IBAS-BPNN的正解精度和運算速度都得到了較大提升，在正解精度方面優于PSO-BPNN，在運算速度上優于BAS-BPNN，因此IBAS-BPNN模型在求解Stewart平臺的正解時具有一定的優越性。

4 結 論

本文在對六自由度并聯平臺的運動學進行分析的基礎上建立了平臺的空間反解模型和優化正解模型，針對BP神經網絡容易陷入局部最優的問題，提出了采用IBAS-BPNN作為平臺的通用正解方法并仿真驗證。結論如下。

1)通過對測試樣本的位置誤差、姿態誤差和誤差百分比分析，驗證了IBAS-BPNN正解方法的適用性，其求解精度較高，解算結果穩定。

2)通過與GA-BP，PSO-BP和BAS-BP對比，驗證了IBAS-BP在求解精度和訓練速度方面的優越性，能夠滿足Stewart平臺精度要求的同時兼顧求解速度的提升。此正解方法可應用于平臺位姿大閉環控制、故障恢復、工作空間分析、試驗過程的實時監控等場景。

在一些平臺應用場景中對精度的要求非常高，本文的方法也難以滿足。今后在現有工作基礎上可以研究數值迭代法，將本文結果作為數值迭代的初值，探索更精確、快速的位姿正解方法。