THE DIRICHLET PROBLEM OF A SPECIAL LAGRANGIAN TYPE EQUATION WITH SUPERCRITICAL PHASE

ZHU Sheng

(School of Mathematics and Statistics,Ningbo University,Ningbo 315211,China)

Abstract:In this paper,we introduce a special Lagrangian type operator,and consider the corresponding Dirichlet problem of the special Lagrangian type equation with supercritical phase.By establishing the global C2estimates,we obtain the existence theorem of classical solutions by the method of continuity.

Keywords: special lagrangian type equation;Dirichlet problem;supercritical phase

1 Introduction

was introduced by Harvey-Lawson[2]in the study of calibrated geometries.Here Θ is a constant called the phase angle.In this case the graphx(x,Du(x))defines a calibrated,minimal submanifold of R2n.Since the work of Harvey-Lawson,special Lagrangian manifolds have gained wide interests,due in large part to their fundamental role in the Strominger-Yau-Zaslow description of mirror symmetry[3].For the special Lagrangian equations with supercritical phase,Yuan obtained the interiorC1estimate with Warren in[4]and the interiorC2estimate with Wang in[5].Recently Collins-Picard-Wu[6]obtained the existence theorem of the Dirichlet problem by adopting the classic method with some important observation about the concavity of the operator.

In fact,the Dirichlet problems of elliptic equations in Rnwere widely studied.For the Laplace equation,the Dirichlet problem was well studied in[7,8].For fully nonlinear elliptic equations,the pioneering work was done by Caffarelli-Nirenberg-Spruck in[1,9]and Ivochkina in[10].In their papers,they solved the Dirichlet problem for Monge-Amp`ere equations andk-Hessian equations elegantly.Since then,many interesting fully nonlinear equations with different structure conditions have been researched,such as Hessian quotient equations,which were solved by Trudinger in[11].For more information,we refer the citations of[9].

In this paper,we establish the following existence theorem of(1.1)

Theorem 1.1Suppose Ω?Rnis aC4strictly convex domain,φ∈C2(?Ω) andwithin.Then there exists a unique solutionu∈to the Dirichlet problem(1.1).

Remark 1.2In addition,if Ω, Θ andφare all smooth,the solutionuis also smooth on.

Remark 1.3As in[6],if we assume there is a subsolutioninstead of the strict convexity of Ω,Theorem 1.1 still holds.

The rest of the paper is organized as follows.In Section 2,we give some properties and establish theC0estimates.In Section 3 and 4,we establish theC1andC2estimates for the Dirichlet problem(1.1).And Theorem 1.1 is proved in the Section 5.

2 Some Properties and a Priori Estimates

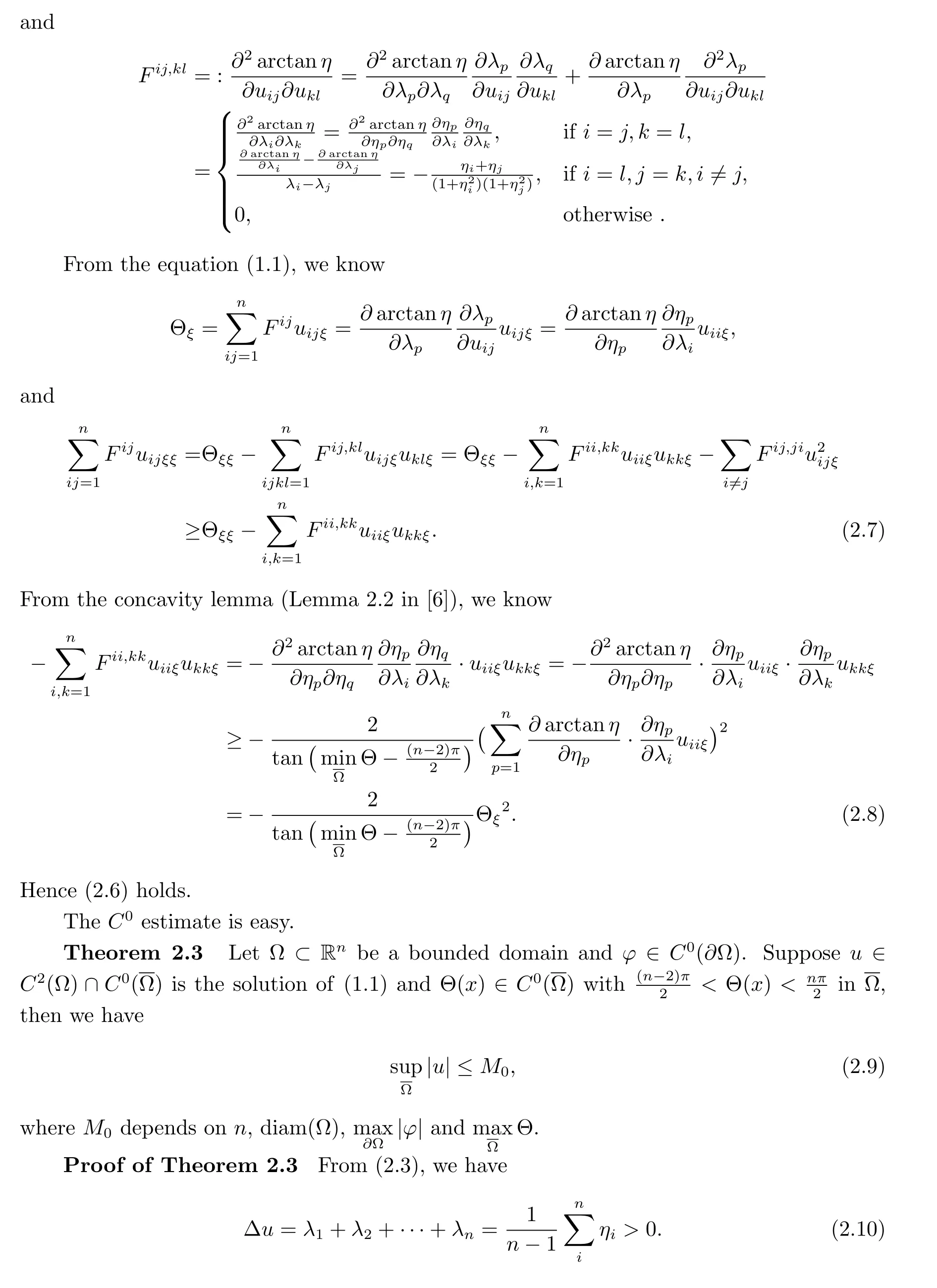
3 Global Gradient Estimate

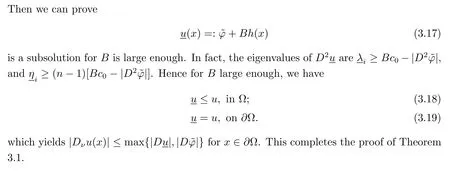
4 Global Second Derivatives Estimate

5 Proof of Theorem 1.1

In this section,we complete the proof of the Theorem 1.1.

For the Dirichlet problem of equation(1.1),we have established theC0,C1andC2estimates in Section 2,3 and 4.By the globalC2priori estimate,the equation(1.1)is uniformly elliptic in.From Property 2.2,we know-e-Aarctanηis concave with respect toD2u,whereAis defined in Property 2.2.Following the discussions in the Evans-Krylov theorem[15,16],we can get the global H?lder estimate of second derivatives,

whereCandαdepend onn,Ω,,|Θ|C2and|φ|C2.From(5.1),one also obtainsC3,α()estimates by differentiating the equation(1.1)and applies the Schauder theory for linear uniformly elliptic equations.

Applying the method of continuity(see[6]),the existence of the classical solution holds.By the standard regularity theory of uniformly elliptic partial differential equations,we can obtain the higher regularity.