優(yōu)化初中數(shù)學(xué)教學(xué) 培養(yǎng)學(xué)生核心素養(yǎng)

?南京市齊武路初級中學(xué) 李繼江

數(shù)學(xué)核心素養(yǎng)并不是確切指某種理論知識，也不是掌握某種數(shù)學(xué)方法，而是學(xué)生在成長過程中需要具備的個人素質(zhì).在數(shù)學(xué)教學(xué)中如何培養(yǎng)學(xué)生的核心素養(yǎng)呢？這就要求教師在核心素養(yǎng)視角下加強數(shù)學(xué)問題研究，從根本上提升學(xué)生的綜合能力，真正發(fā)展學(xué)生運用數(shù)學(xué)知識與方法發(fā)現(xiàn)、提出、分析和解決問題的能力，從而在學(xué)習(xí)過程中形成數(shù)學(xué)學(xué)科的核心素養(yǎng).下面就如何優(yōu)化教學(xué)策略以提高學(xué)生核心素養(yǎng)談?wù)勛约旱淖龇?

1 讓數(shù)學(xué)問題走進生活，激發(fā)學(xué)生學(xué)習(xí)興趣

蘇科版教材中“數(shù)學(xué)活動”有這樣的一個示例：算“24”是一種常見的撲克牌游戲.我們約定一副撲克牌中的黑色數(shù)字為正數(shù)，紅色數(shù)字為負數(shù)，J表示11，Q表示12，K表示13，A為1，2張JOKER均為0.將一副撲克牌平均分給每個人，每人每次出4張牌.4張牌的點數(shù)都是1～13中的某個數(shù).

游戲中，小強抽到以下4張牌：方片2，黑桃5，梅花J,紅桃Q.請你用這四張牌表示的數(shù)寫出運算結(jié)果為24的算式(寫出1個)．

有理數(shù)的混合運算就自然而然地融入到了數(shù)學(xué)游戲之中，在教學(xué)中，學(xué)生的學(xué)習(xí)興趣也就自然增加了.這樣的情境下，打撲克游戲已經(jīng)不是純粹地玩，而是一種益智活動.持續(xù)開展數(shù)學(xué)游戲活動，學(xué)生會在玩中發(fā)現(xiàn)更多更奇妙的游戲規(guī)則，也會發(fā)現(xiàn)或者提出更多有意義的數(shù)學(xué)問題.

再如一些教材中出現(xiàn)的“七巧板”活動.七巧板起源于我國先秦時期，古算書《周髀算經(jīng)》中有關(guān)于正方形的分割術(shù)．據(jù)清代陸以湉《冷廬雜識》記載，七巧板是由宋代黃伯思設(shè)計的“宴幾”圖演變而來的，原為文人的一種室內(nèi)游戲，后在民間逐步演變?yōu)槠磮D版玩具．教材借助折疊七巧板活動，不但引導(dǎo)學(xué)生通過動手實踐，認識七巧板的多種幾何形狀，更加激發(fā)了學(xué)生的學(xué)習(xí)或研究興趣，從簡單的圖形，到形象逼真的圖象，再到富有內(nèi)涵的幾何標志，等等，不斷地激發(fā)著數(shù)學(xué)愛好者層層深入，獲得更多更豐富的內(nèi)容.

2016年第七屆世界歷史文化名城博覽會在南京舉辦．以“多元，開放，創(chuàng)造”為定位，其會徽是運用“七巧板”元素組合而成的“一件云錦嫁衣”圖案，由國際著名平面設(shè)計大師、荷蘭艾因霍芬設(shè)計學(xué)院院長托馬斯設(shè)計完成．

隨著數(shù)學(xué)知識的深入學(xué)習(xí)，對圖形的簡單認識逐漸過渡到數(shù)學(xué)計算.例如，某市人民正在積極開展創(chuàng)建“全國文明城市”的運動，聰明的學(xué)生用七巧板拼成一副孔子像，并通過相關(guān)數(shù)據(jù)計算孔子像的高度．

讓數(shù)學(xué)問題走進生活，可以逐步培養(yǎng)學(xué)生從數(shù)學(xué)角度觀察現(xiàn)實世界的意識和習(xí)慣，從而不斷地激發(fā)學(xué)生的好奇心和探究興趣.

2 加強數(shù)學(xué)問題規(guī)律研究，調(diào)動學(xué)生的探究意識

蘇科版八年級上冊數(shù)學(xué)教材中“數(shù)學(xué)活動——探尋勾股數(shù)”中，從簡單的圖形入手，探尋勾股數(shù)的存在規(guī)律，意在調(diào)動學(xué)生的探究意識.在了解基本勾股數(shù)之后，繼續(xù)深入探尋“勾股數(shù)”：直角三角形三邊長是整數(shù)時我們稱之為“勾股數(shù)”，那么勾股數(shù)有多少？勾股數(shù)有規(guī)律嗎？在引導(dǎo)學(xué)生探究的過程中，明確勾股數(shù)的基本特點，即“兩個數(shù)的平方和(或差)等于第三個數(shù)的平方”，從而確定了勾股數(shù)滿足的形式：( )2+( )2=( )2；或( )2-( )2=( )2.我們已經(jīng)知道(x+y)2-(x-y)2=4xy，如果等式右邊的4xy也能轉(zhuǎn)化為某正整數(shù)平方的形式，就能滿足勾股數(shù)的形式了.通過再次探究，假設(shè)x=m2，y=n2，m，n為任意正整數(shù)且m>n，則恰好能實現(xiàn)這一要求，即有(m2-n2)2+(2mn)2=(m2+n2)2，從而得出了勾股數(shù)滿足的條件.

結(jié)合本例我們發(fā)現(xiàn)，如果深入探究生活中的小問題或者數(shù)學(xué)情境，發(fā)現(xiàn)其中涵含的數(shù)學(xué)規(guī)律，學(xué)生講道理、有條理的思維品質(zhì)也會逐步養(yǎng)成.

在學(xué)習(xí)了“用字母表示數(shù)”這一節(jié)后，教材補充了“閱讀”內(nèi)容，這部分內(nèi)容表述如下：人們通過長期觀察發(fā)現(xiàn)，如果早晨天空中有棉絮狀的高積云，那么午后常有雷雨降臨，于是有了“朝有破絮云，午后雷雨臨”的諺語.緊跟著提出了數(shù)學(xué)問題：三角形有3個頂點，如果在它的內(nèi)部再畫n個點，并以這(n+3)個點為頂點畫三角形，那么最多可以剪得多少個這樣的三角形？如何解決此類的問題？引導(dǎo)學(xué)生學(xué)會探究歸納：為了解決這個問題，我們可以從n=1，n=2，n=3等具體、簡單的情形入手，探索最多可以剪得的三角形個數(shù)的變化規(guī)律．

此類問題的解決，在一步步引導(dǎo)學(xué)生觀察、比較中深入發(fā)展下去，并借助計算、推理發(fā)現(xiàn)其存在的規(guī)律，不知不覺中讓學(xué)生構(gòu)建了數(shù)學(xué)邏輯體系，并培養(yǎng)了良好的科學(xué)態(tài)度與理性精神.

3 引導(dǎo)數(shù)學(xué)問題模型化，培養(yǎng)學(xué)生模型觀念

將數(shù)學(xué)問題簡約化，其實就是將模型觀念融入數(shù)學(xué)問題之中，借助對數(shù)學(xué)模型的運用解決實際問題，并能有清晰的認識.

教材在“一元二次方程”后的“數(shù)學(xué)活動”中提出這樣的問題：在一塊長33 m，寬24 m的矩形綠地內(nèi)，要圍出一個花圃，使花圃的面積是矩形面積的一半，你能給出設(shè)計方案嗎？再進一步引發(fā)學(xué)生思考：花圃可以有多種設(shè)計方案，例如，在綠地中間可以開辟一個矩形的花圃，使四周的綠地等寬，綠地的面積與花圃的面積相等，你能計算出綠地的寬嗎？通過對數(shù)學(xué)問題情境的分析，可以建立一元二次方程模型解答，從而將復(fù)雜問題簡單化.基本問題得到解決后，再引導(dǎo)學(xué)生進一步探索：請你再設(shè)計兩種不同的方案，并交流你設(shè)計的方案有哪些特點.通過提出的問題，充分考查學(xué)生的思維開放性、應(yīng)用數(shù)學(xué)的意識及探索能力，不但涉及學(xué)生的畫圖設(shè)計能力，還有動手操作的能力.

當然這類問題在古代數(shù)學(xué)文化中也屢見不鮮.明朝數(shù)學(xué)家程大位在數(shù)學(xué)著作《直指算法統(tǒng)宗》中以《西江月》詞牌敘述了一道“蕩秋千“問題：平地秋千未起，踏板一尺離地．送行二步與人齊，五尺人高曾記．仕女佳人爭蹴，終朝笑語歡嬉．良工高士素好奇，算出索有幾？如果我們僅僅是針對著作中表述的問題去理解分析，可能對學(xué)生來說，難上加難，然而，將難懂的古文言文字轉(zhuǎn)化為現(xiàn)代漢語來理解問題則簡單易懂.譯文：如圖1，有一架秋千，當它靜止時，踏板離地1尺，將它往前推送10尺(水平距離)時，秋千的踏板就和人一樣高，這個人的身高為5尺，秋千的繩索始終拉得很直，試問繩索有多長？(注古代5尺為1步)結(jié)合圖形，文字內(nèi)容更加生動形象，如圖2所示，將描述性問題轉(zhuǎn)化為數(shù)學(xué)模型來解答，真正讓學(xué)生感受到數(shù)學(xué)語言的魅力.

圖1

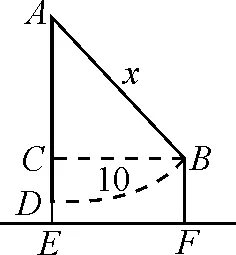
圖2

數(shù)學(xué)模型如下：如圖2，秋千繩索AD靜止的時候，踏板離地高一尺(DE=1尺)，將它往前推進兩步(CB=10尺)，此時踏板升高離地五尺(BF=5尺)，已知AE⊥EF于點E，BF⊥EF于點F，BC⊥AE于點C，AD=AB．請解答下列問題：(1)四邊形ECBF是哪種特殊的四邊形？請證明你的結(jié)論；(2)求AB的長．

4 將數(shù)學(xué)問題實際操作化，增強學(xué)生的應(yīng)用意識

數(shù)學(xué)中的有些問題，我們只有通過具體操作后，才能更好地理解把握，才能更好地進行應(yīng)用.因此很多問題需要我們在實踐中落實，讓問題實踐化，更容易調(diào)動學(xué)生的積極性，增強他們的應(yīng)用意識.

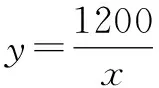
還有的問題更接近學(xué)生的日常生活，如涉及物理學(xué)科的問題：一定電壓(V)下電流I(A)和電阻R(Ω)之間成反比例關(guān)系，小明用一個蓄電池作為電源組裝了一個電路，通過實驗，發(fā)現(xiàn)電流I(A)隨著電阻R(Ω)值的變化而變化的一組數(shù)據(jù)如表1所示．

表1 電流與電壓實驗數(shù)據(jù)

根據(jù)上述表述進一步提出問題：求這個蓄電池的電壓值；請在坐標系中，通過描點畫出電流I和電阻R之間的關(guān)系圖象，并直接寫出I和R之間的函數(shù)關(guān)系式；若該電路的最小電阻值為1.5 Ω，請求出該電路能通過的最大電流．

諸如上述教材中都可能涉及到的相關(guān)材料，都是在引導(dǎo)學(xué)生關(guān)注生活中與數(shù)學(xué)相關(guān)的信息，激發(fā)學(xué)生的社會參與意識，并主動參與到數(shù)學(xué)活動中，感受數(shù)學(xué)的實際應(yīng)用價值，體會數(shù)學(xué)的奧妙.

總之，教師只要充分利用教材典型材料，將其融入生活中，及時歸納總結(jié)，并引導(dǎo)學(xué)生不斷用數(shù)學(xué)語言進行問題交流，了解并領(lǐng)會數(shù)學(xué)的價值，欣賞數(shù)學(xué)的美，建立學(xué)好數(shù)學(xué)的信心，真正形成數(shù)學(xué)思想，形成質(zhì)疑問難、勇于探索的科學(xué)精神.Z