基于波形特征和決策樹分類算法的巖體破裂信號識別

龍 翼，王培武，皇甫風成，陳天曉，徐世達

(1.紫金礦業集團股份有限公司，福建 龍巖 364000；2.東北大學深部金屬礦山安全開采教育部重點實驗室，遼寧 沈陽 110819)

微震信號識別是開展礦山開采過程微震監測的基礎。近年來，隨著礦山開采深度增加和高強度開采模式的推廣，采場(巷道)圍巖破壞日趨凸顯，嚴重時甚至會引起巖爆、冒落等災害。謝和平等[1]國內學者指出在高應力條件下，巖爆已成為礦山巖體的重要災害之一。目前，微震監測技術已被廣泛應用于巖爆、大體積冒落等災害監測。該技術利用巖體破裂時發出的彈性波來監測巖體的穩定性。但由于礦山施工環境復雜，爆破振動、大型用電設備干擾等因素導致微震監測系統接收到除巖體破裂外的多種干擾信號。因此，巖體破裂信號識別是開展巖體穩定性評估及破壞失穩災害風險評估的前提。ALLMANN等[2]提出了一種基于P波波譜與震源模型均方根擬合差的爆破信號與巖體破裂信號識別方法；朱權潔等[3]基于小波分析和分形理論提出了現場微震監測信號識別方法；MALOVICHKO[4]引入地震學信號識別技術，考慮發生時間、輻射模式、低頻帶與高頻帶能量分布和相鄰波形相關系數特征參數，采用最大似然法對巖體破裂波形進行識別；VALLEJOS等[5]采用邏輯回歸與神經網絡建立了基于震源參數的高精度微震事件識別模型；ZHAO等[6]采用頻率切片小波變換技術分解信號的方法，對兩類信號不同的能量分布特性進行了對比研究；SHANG等[7]通過經驗模態分解和奇異值分解進行波形特征提取與波形分類，識別準確率能夠達到88.25%；ZHANG等[8]提出了基于變分模態分解的微震信號特征提取及分類辨識方法；羅小燕等[9]提出了一種基于改進變分模式分解算法(VMD)和GA-BP神經網絡的預測方法，提取信號能量特征參數作為模型的輸入構建GA-BP預測模型，準確率達90%；XU等[10]建立了巖體破裂信號神經網絡識別模型，有效剔除了現場噪音信號的干擾。

本文針對阿舍勒銅礦微震監測系統采集信號，分析阿舍勒深部采區不同類型波形特征參數差異，開展波形特征參數與波形類型相關性分析，建立決策樹算法波形識別模型，實現阿舍勒銅礦微震監測巖體破裂波形自動識別，減少微震數據處理人工工作量，提高巖體破裂信號識別精度，消除噪音信號的干擾。

1 決策樹算法

決策樹算法是監督學習中的一種，常被用來解決回歸和分類問題[11]。“完全生長”的決策樹因為結構簡單直觀，具有很強的解釋性，已被廣泛應用。一棵完整的決策樹包含特征選擇、決策樹構建、剪枝三個過程。

常用的決策樹算法主要有ID3、C4.5、CART等。ID3算法核心是在各個節點上應用信息增益準則選擇特征，構建決策樹。ID3算法未進行剪枝，決策樹的結構可能過于復雜，易產生過擬合問題。C4.5算法需要對數據進行多次順序掃描和排序，效率較低。本文選用更適用于多變量組合決策的CART算法進行分類。

1.1 CART算法決策樹生長

決策樹中的CART算法生成的決策樹是二叉樹，每一次分裂會產生兩個子節點，其主要由分類樹的生成和剪枝處理組成。CART分類樹預測分類離散型數據，使用基尼指數(Gini)選擇最優特征，同時決定該特征的最優二值切分點。分類過程中，假設有k個類，樣本點屬于第k個類的概率為Pk，則概率分布的基尼指數定義為式(1)。

(1)

根據基尼指數定義，可以得到樣本集合D的基尼指數見式(2)。

(2)

式中，Ck為數據集D中屬于第k類的樣本子集。

數據D根據特征A在某一取值a上進行分割，得到D1、D2兩部分后，特征A下集合D的基尼系數見式(3)。

Gain_Gini(D,A)=

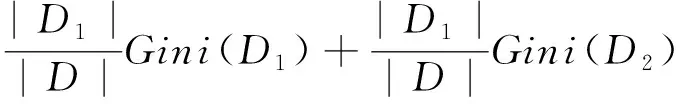
(3)

式中：Gini(D)為集合D的不確定性；Gini(D，A)為A=a分割后集合D的不確定性。基尼指數越大，樣本集合的不確定性越大。

對于屬性A，分別計算任意屬性值將數據劃分為兩部分之后的Gain_Gini，選取其中的最小值，作為屬性A得到的最優二分方案。然后對于訓練集S，計算所有屬性的最優二分方案，選取其中最小值，作為樣本的最優二分方案，見式(4)和式(5)。

min(Gain_Gini(D,A))

(4)

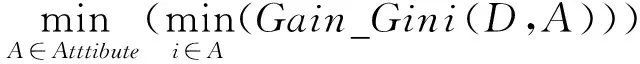
(5)

1.2 決策樹剪枝

剪枝是決策樹學習算法中解決過擬合問題的主要手段[12]。思路是從已生成的分類樹中剪掉一些子樹或者葉子節點，并將根節點或者父節點作為新葉子節點，以便簡化分類樹模型。決策樹剪枝往往是通過極小化決策樹的整體損失函數或者代價函數。設樹的葉子節點為|T|，葉子節點t上有Nt個樣本點，其中k類的樣本點數為Nkt，Ht(T)為結點t上的經驗熵，α≥0，所以損失函數定義為式(6)。

(6)

經驗熵為式(7)。

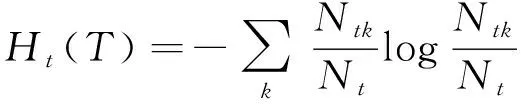
(7)

可得式(8)。

C(T)=C(T)+α|T|

(8)

式中：C(T)為對訓練數據的預測誤差；|T|為模型的復雜度。損失函數表達兩者之間的平衡。

2 典型信號波形特征分析

2.1 信號類型

依據現場人工標定，阿舍勒銅礦微震監測系統采集波形主要有電氣噪音信號、爆破振動信號、機械振動信號和巖石破裂信號(圖1)。電氣噪音信號一般是由于微震數據傳輸線路靠近井下用電設備產生的，該類信號具有明顯的周期性，較容易分辨；爆破振動信號是現場爆破引發的，該信號一般連續出現多次，與爆破段數呈現出較好的相關性；機械振動信號是由機械振動、鑿巖等產生的振動波，波形雜亂無章，無明顯的規律性；巖體破裂信號較規則，衰減規律性較好。

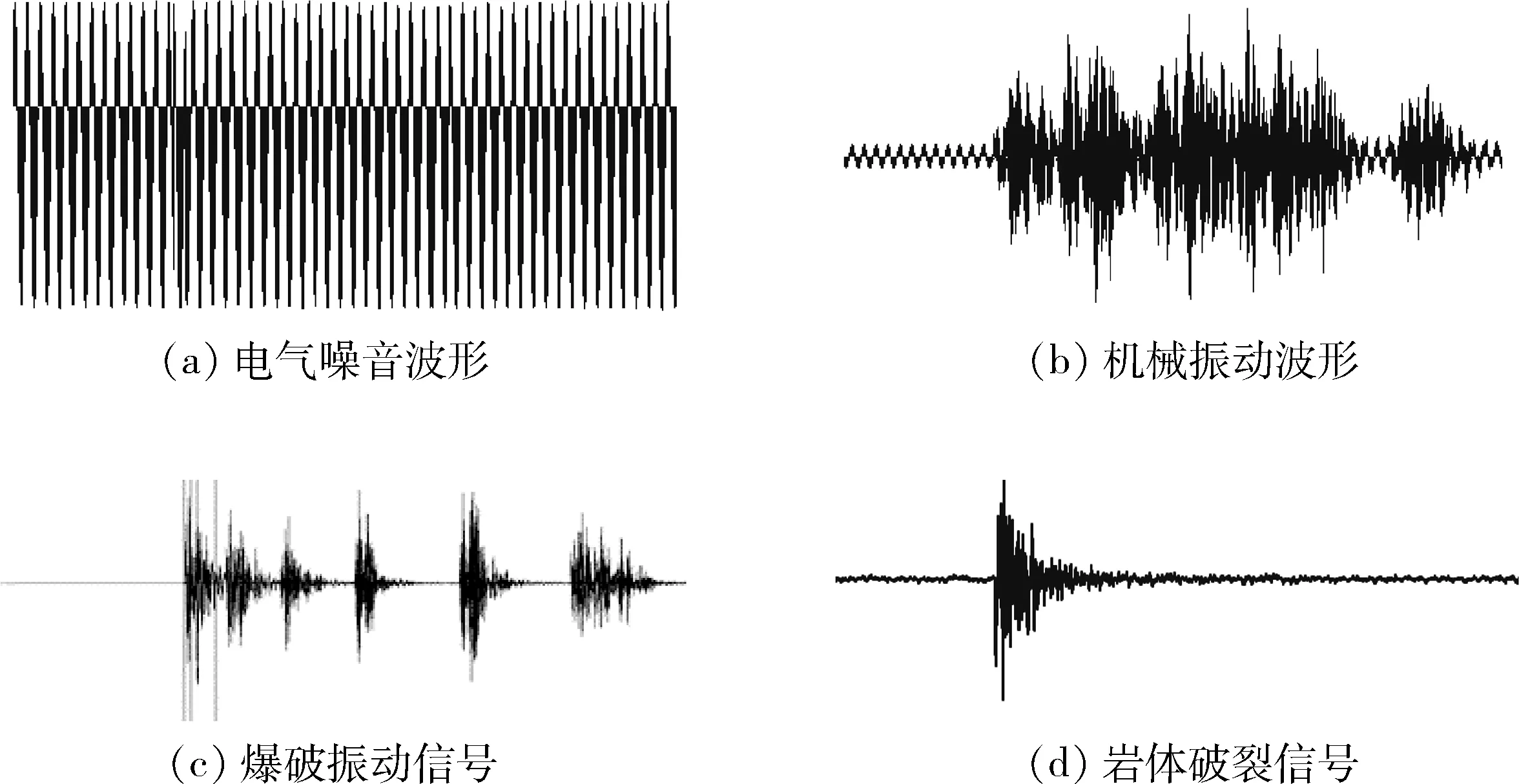
圖1 典型信號波形Fig.1 Waveform of typical signal

2.2 信號波形特征分析

常見的波形參數主要有振鈴數、持續時間、最大振幅等，如圖2所示。通過Matlab軟件開發的波形參數提取程序，實現微震信號波形參數提取。阿舍勒銅礦機械振動信號的振鈴數較高，最小值為89，最大值為301，均值遠遠高于其他三種信號，但從平方差來看電氣噪聲信號最為穩定；機械振動信號上升振鈴數也遠高于其他三種信號，均值達105.82，其他三種信號的上升振鈴數均小于30；在上升時間指標中，巖體破裂信號與爆破振動信號較為接近，都在0.25～30 ms范圍，電氣噪聲信號和機械振動信號表現接近，區間主要在10～1 000 ms，平均值遠高于前兩者；在持續時間這一指標中，爆破振動信號與巖體破裂信號的均值接近但遠小于機械振動信號和電氣噪聲信號的均值，巖體破裂信號的均值在50 ms左右，最大值為102.5 ms，機械振動信號和電氣噪聲信號的最小值均大于400 ms；爆破振動信號最大振幅的均值最大，機械振動信號與電氣噪聲信號的最大振幅均值接近；電氣噪聲信號的主頻均值遠小于其他三種信號。

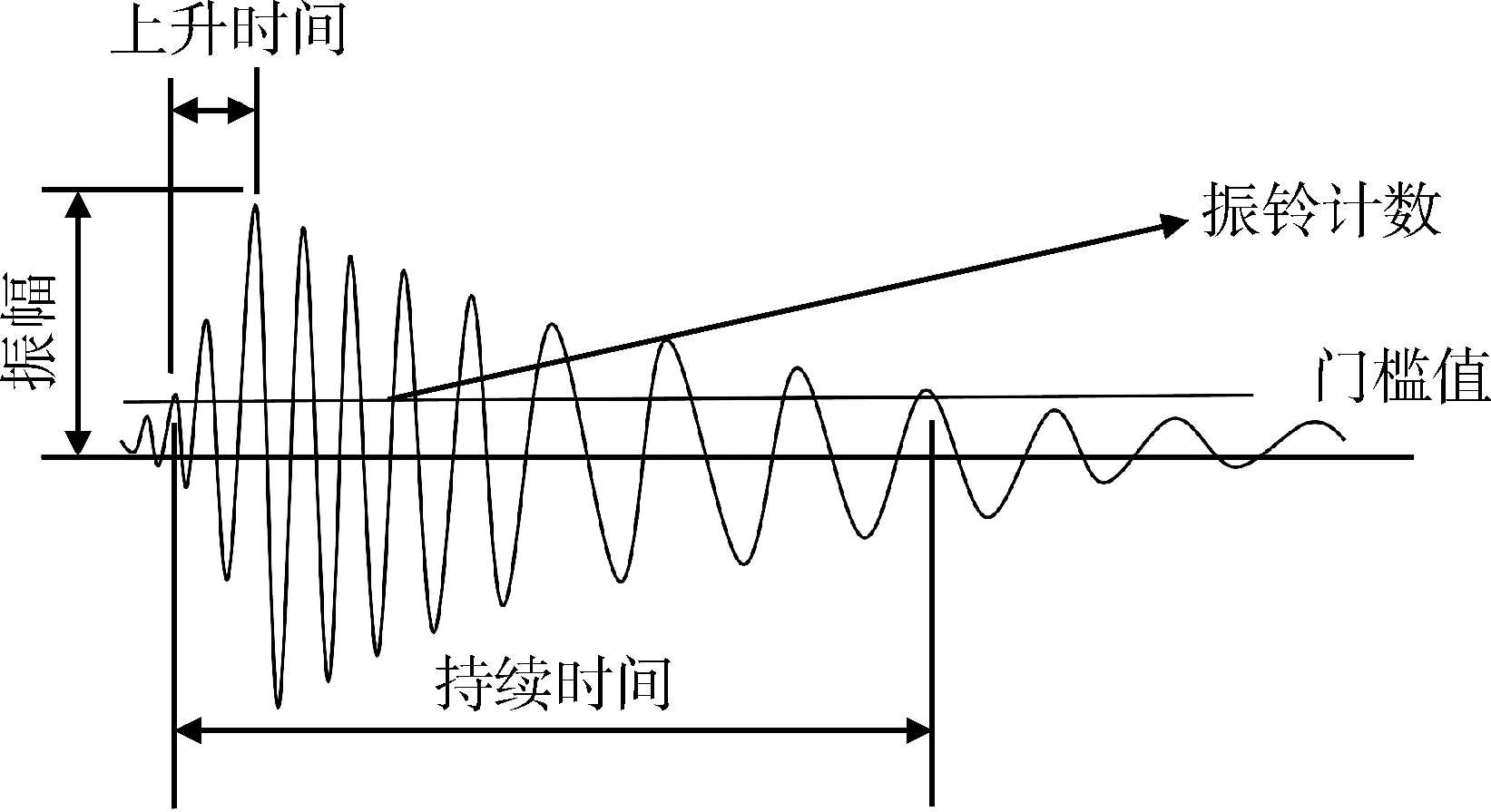
圖2 聲發射信號波形參數示意圖Fig.2 Waveform parameters of acoustic emission

不同波形特征參數分布小提琴圖如圖3所示。四種典型信號在振鈴數、上升振鈴數、上升時間、最大振幅、主頻參數分布均有不同程度的重合，而持續時間有較大區別。電氣噪音信號與機械振動信號持續時間明顯大于巖體破裂信號與爆破振動信號，但巖體破裂信號與爆破振動信號持續時間無明顯區別。值得注意的是，在上升時間、最大振幅等參數方面，爆破振動信號與巖體破裂信號存在一定差異。由此可見，僅依靠一種特征參數無法有效識別出巖體破裂信號。

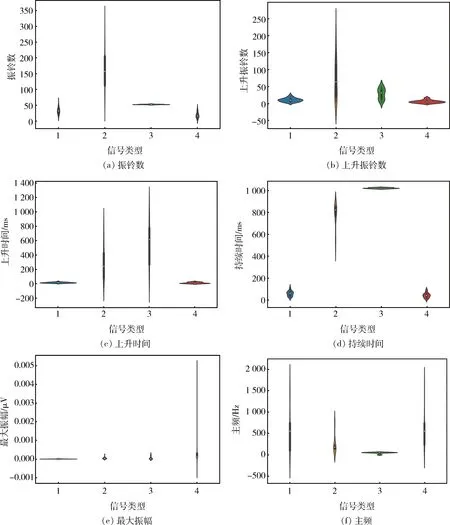
1-巖體破裂信號；2-機械振動信號；3-電氣噪聲信號；4-爆破震動信號

根據皮爾遜相關性計算可以得出，巖體破裂信號和爆破振動信號波形與振鈴數、上升振鈴數、上升時間、持續時間、最大振幅、主頻六個變量之間的相關性系數分別為0.549 5、0.478 4、0.356 7、0.386 2、0.419 5、0.477 5，如圖4所示。由圖4可知，上升時間、持續時間與信號類型相關性相對較低，但仍然大于0.35。其他四個參數與信號類型相關性明顯高于上升時間和持續時間。因此，為提高準確率，將六種波形特征參數一起輸入模型識別巖體破裂信號。

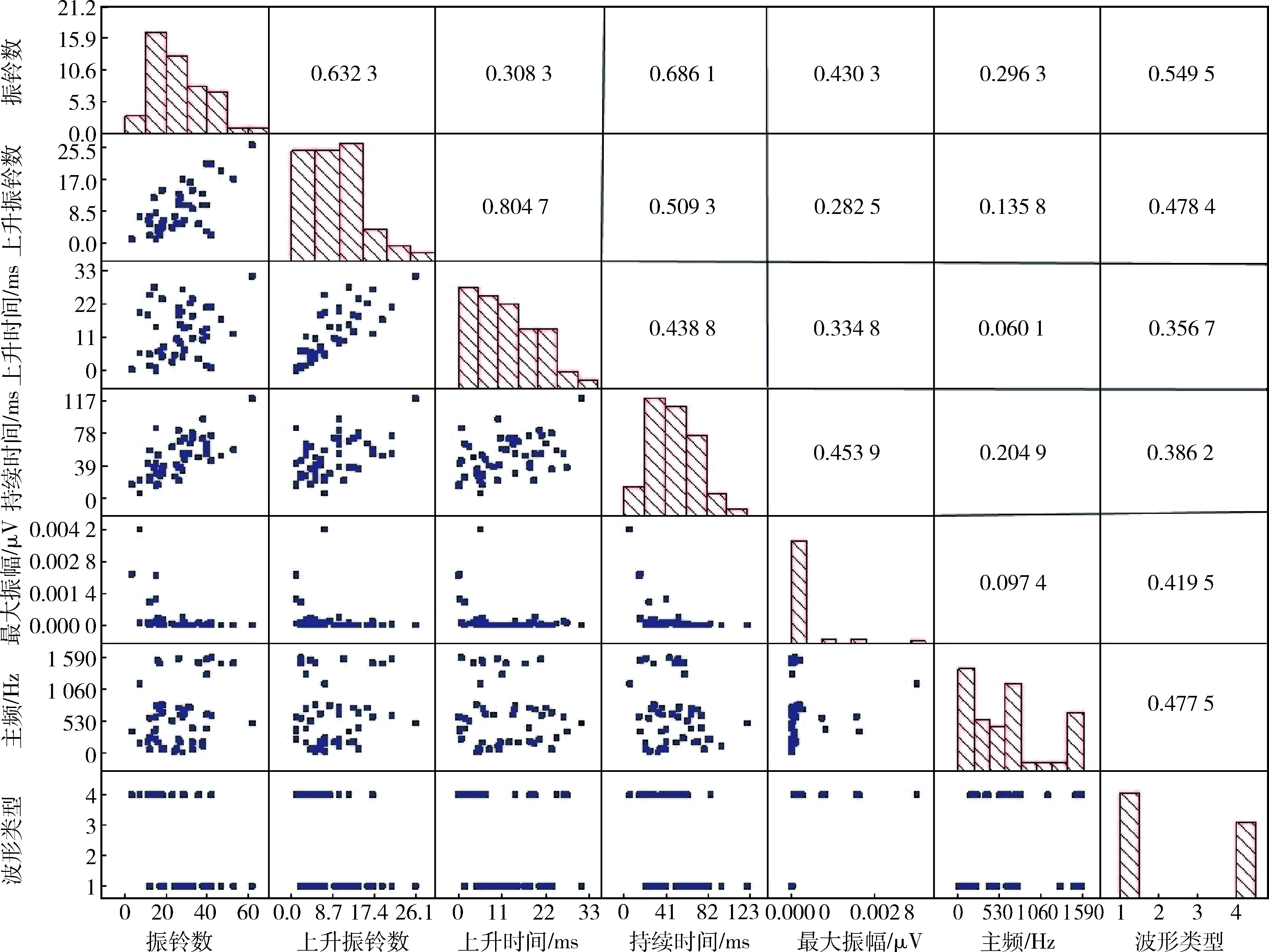
圖4 信號類型與波形特征參數的矩陣散點圖Fig.4 Matrix scatter plot of signal type and waveform characteristic parameters

3 基于決策樹分類的信號識別

從阿舍勒銅礦微震監測數據中選取248組四種典型信號數據，電氣噪音信號59組，爆破振動信號55組，巖體破裂信號75組，機械振動信號59組。令巖體破裂信號為1，機械振動信號為2，電氣噪聲信號為3，爆破振動信號為4。其中，92組用于訓練，156組用于模型測試。經過訓練后的模型中，六個特征值的重要性差異較大，各特征經計算重要性得出，振鈴數的權重系數為0.23，持續時間的權重系數為0.50，最大振幅的權重系數為0.27，上升振鈴數、上升時間和主頻的權重均為0。這說明，持續時間在識別巖體破裂信號中作用最大，其次是最大振幅和振鈴數。基尼指數也稱基尼不純度，表示一個隨機選中的樣本在子集中被分錯的可能性，其值越小，選擇該屬性作為分裂屬性的效果越好。92組樣本中，持續時間的基尼指數為0.75，小于其他屬性的基尼指數，選作根節點。重復計算基尼指數，直至基尼指數為0，單個樣本歸類完成。此時，因為所有屬性都會被考慮作為節點，模型詳細且龐大，所以也造成了過擬合問題，對于訓練數據外的樣本識別效果并不好。為解決該問題，對模型進行剪枝處理，去掉一些節點。最終訓練出的決策樹模型，如圖5所示。

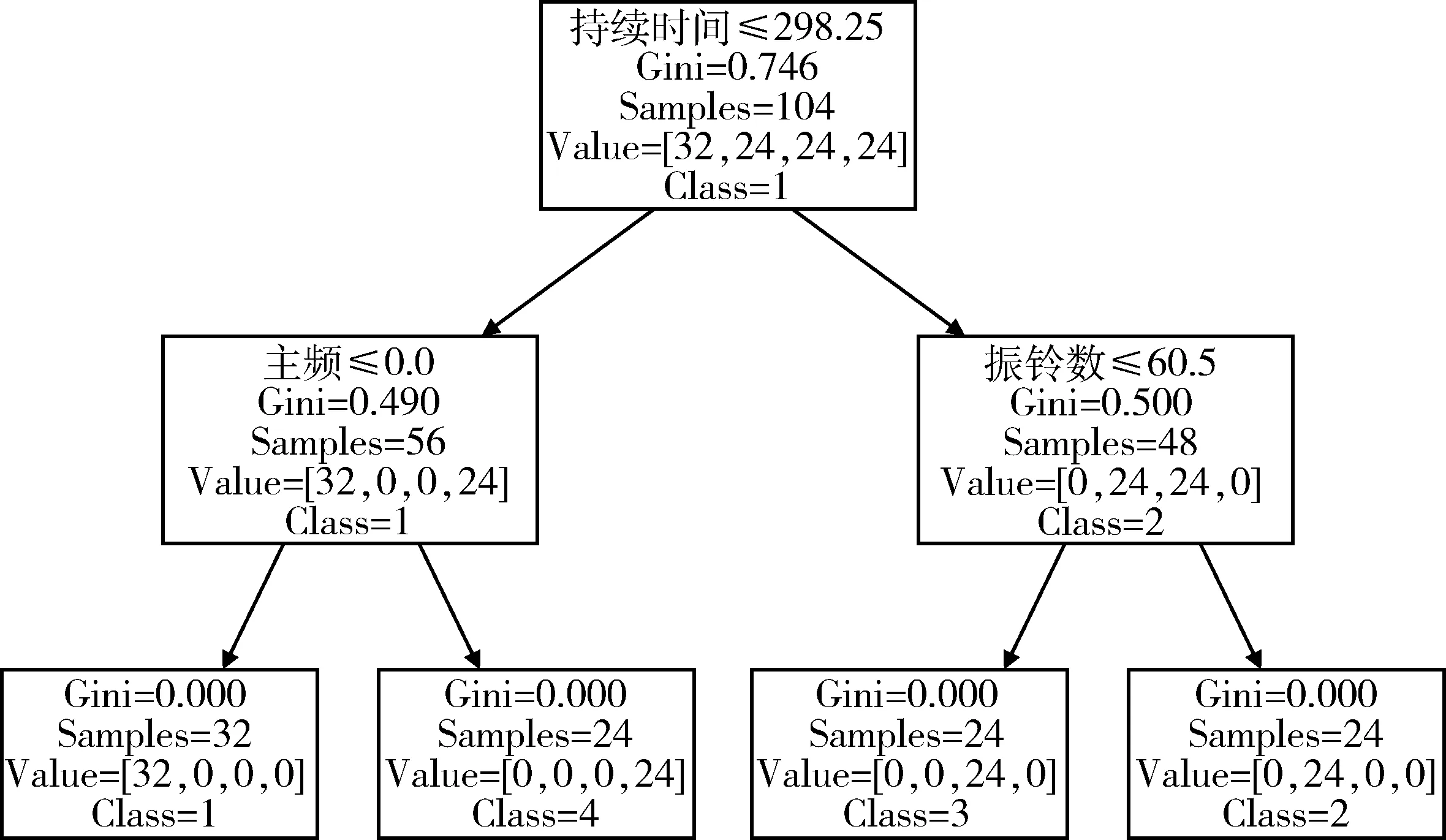
圖5 決策樹識別流程圖Fig.5 The identification process of decision tree algorithm

將156個檢驗數據輸入建立的信號識別決策樹模型，正確識別156個信號，錯誤識別2個信號，識別準確率達98.3%。其中，爆破振動信號34個，準確識別33個，準確率97.1%；巖體破裂信號46個，準確識別45個，準確率97.8%；機械振動信號和電氣噪音信號個數都為38個，全部準確識別，準確率100%。

4 模型結果及對比

支持向量機(SVM)是VANIK研究團隊1955年在統計學理論基礎上提出的一種機器學習方法[13]，較好地解決了很多學習方法的小樣本、非線性、高維數、局部極小點等難點問題，具有良好的推廣前景。本文通過建立SVM模型驗證決策樹分類算法的可靠性。模型建立時，選取高斯徑向基函數(RBF函數)作為核函數。為避免SVM模型出現過擬合情況，并最大程度保證其泛化能力，該模型的懲罰參數選用0.65。在保證兩種模型效果對比公平可靠的前提下，SVM建立后訓練數據同樣選擇92組，檢測數據選擇156組。最終156組數據里，識別錯誤的組數為34組，其成功率為78.2%，其中，電氣噪音信號的識別準確率為100%，爆破振動信號的識別準確率為64.7%，機械振動信號的識別準確率為100%，巖體破裂信號的識別準確率為73.9%。

決策樹模型98.3%的識別準確率明顯高于SVM模型78.2%的識別準確率。不同類型波形識別準確率如圖6所示。從各類信號的識別準確度對比中可以看出，在識別巖體破裂信號與爆破波形信號時存在問題，這主要是因為兩類波形參數分布范圍較重合，識別難度較高。顯然，決策樹模型巖體破裂信號與爆破振動信號識別能力明顯高于SVM模型。

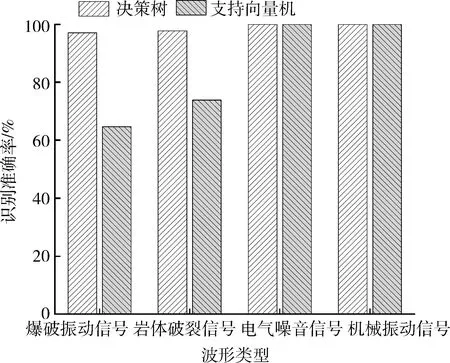
圖6 模型識別準確率對比圖Fig.6 Comparison of model recognition results accuracy

5 結 論

本文采用決策樹分類中的CART算法建立礦山巖體信號識別模型，得出主要結論如下所述。

1) 巖體破裂信號和爆破波形信號特征參數較相近，識別難度大，僅依靠單一的參數無法從眾多類型信號中有效識別出巖體破裂信號。

2) 振鈴數的權重系數為0.23，持續時間的權重系數為0.50，最大振幅的權重系數0.27，說明持續時間在識別巖體破裂信號中作用最大，其次是最大振幅和振鈴數。

3) 由決策樹模型檢測從阿舍勒銅礦獲取的波形信號，巖體破裂信號的識別準確率達到97.8%，各類信號的識別準確率均遠高于常用的SVM模型，可以有效節省信號識別的人力和時間。