考慮最大線應(yīng)變理論的多重破壞機(jī)制PMC強(qiáng)度模型

李曉光，周春雷，范棟玨,3，張力天，鄭益武

(1.北京科技大學(xué)，北京 100083；2.軍委機(jī)關(guān)事務(wù)管理總局工程代建管理辦公室，北京 100082；3.北京科技大學(xué)順德創(chuàng)新學(xué)院，廣東 佛山 528399)

深部開采條件下，高應(yīng)力、強(qiáng)擾動(dòng)誘發(fā)的巖石破壞過(guò)程表現(xiàn)出明顯非線性行為和破壞機(jī)制的轉(zhuǎn)化特征，在此過(guò)程中巖石伸長(zhǎng)、剪切及壓密屈服等多種破壞機(jī)制共生。不同圍巖下巖石表現(xiàn)出不同的破壞模式，巖石在拉力狀態(tài)或者較低壓力水平下表現(xiàn)為拉破壞，隨著壓力逐漸上升，巖石破壞模式從拉破壞向剪切破壞過(guò)渡，深部較高應(yīng)力水平下巖石破壞模式從常規(guī)剪切破壞向孔隙坍塌型破壞轉(zhuǎn)化。因此，巖石表現(xiàn)出拉破壞、剪切破壞和壓剪屈服等多種破壞模式過(guò)渡的現(xiàn)象。

PAUL[1-2]在Mohr Coulomb模型基礎(chǔ)上考慮中間主應(yīng)力的影響，提出了包含三個(gè)主應(yīng)力的表達(dá)式，并從單軸壓縮、統(tǒng)一三軸(各向同性)伸長(zhǎng)和單軸伸長(zhǎng)的應(yīng)力狀態(tài)確定了三個(gè)參數(shù)常量。MEYER等[3]將其發(fā)展為PMC強(qiáng)度準(zhǔn)則，針對(duì)巖石材料的破壞機(jī)理轉(zhuǎn)化特征，以PMC模型為基礎(chǔ)，討論了十二邊形PMC破壞面的形狀，通過(guò)擬合兩個(gè)破壞平面來(lái)描述非線性破壞面，發(fā)展出十二面椎體PMC模型，其模型能夠觀察到隨著平均應(yīng)力的增加破壞面的形狀變化，可以表征巖石材料隨應(yīng)力條件上升由拉斷破壞向剪切破壞轉(zhuǎn)變的特征。在材料參數(shù)方面，MAKHNENKO等[4]提出了一個(gè)平面擬合方法，依據(jù)數(shù)據(jù)點(diǎn)和破壞面的正交距離平方和最小值進(jìn)行求解；ZENG等[5]提出了采用最小二乘法擬合參數(shù)；DEHLER等[6]提出了簡(jiǎn)化的PMC模型，假設(shè)拉伸和壓縮條件下摩擦角相同，使十二邊形PMC減少了兩個(gè)參數(shù)，僅包含四個(gè)參數(shù)。

本文研究以最大線應(yīng)變理論、PMC過(guò)渡型準(zhǔn)則為理論基礎(chǔ)，擬合現(xiàn)場(chǎng)、室內(nèi)試驗(yàn)數(shù)據(jù)，提出適合深部巖體破壞模式過(guò)渡特征的強(qiáng)度理論，并能夠揭示巖體低強(qiáng)度破壞內(nèi)在機(jī)理。

1 PMC理論

PAUL[1-2]在1968年考慮中間主應(yīng)力的影響，提出了PMC模型；MEYER等[3]在2013年將其發(fā)展為PMC強(qiáng)度準(zhǔn)則，其主應(yīng)力的表達(dá)式見式(1)。

Aσ1+Bσ2+Cσ3=1

(1)

式中：A、B、C為材料常數(shù)，表達(dá)式見式(2)～式(4)。當(dāng)B=0時(shí)，式(1)變?yōu)镸C強(qiáng)度準(zhǔn)則。

(2)

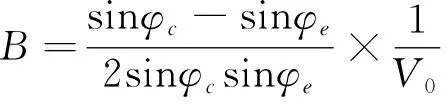
(3)

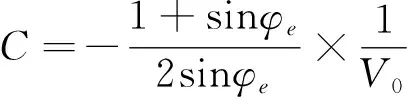
(4)

式中：φc、φe分別為壓縮時(shí)內(nèi)摩擦角和伸長(zhǎng)時(shí)內(nèi)摩擦角；V0為理論三軸抗拉強(qiáng)度。

將三個(gè)參數(shù)代入式(1)，用兩個(gè)內(nèi)摩擦角和頂點(diǎn)表示見式(5)。

(5)

PMC破壞準(zhǔn)則在主應(yīng)力空間構(gòu)建了一個(gè)有共同頂點(diǎn)V0的破壞面，PMC準(zhǔn)則利用巖石材料在壓縮和拉伸時(shí)摩擦角的不同來(lái)考慮中間主應(yīng)力的影響，是一個(gè)包含三個(gè)主應(yīng)力的多軸線性破壞準(zhǔn)則，包含的三個(gè)材料參數(shù)可通過(guò)巖石常規(guī)三軸實(shí)驗(yàn)得到，PMC模型破壞包絡(luò)線如圖1所示。

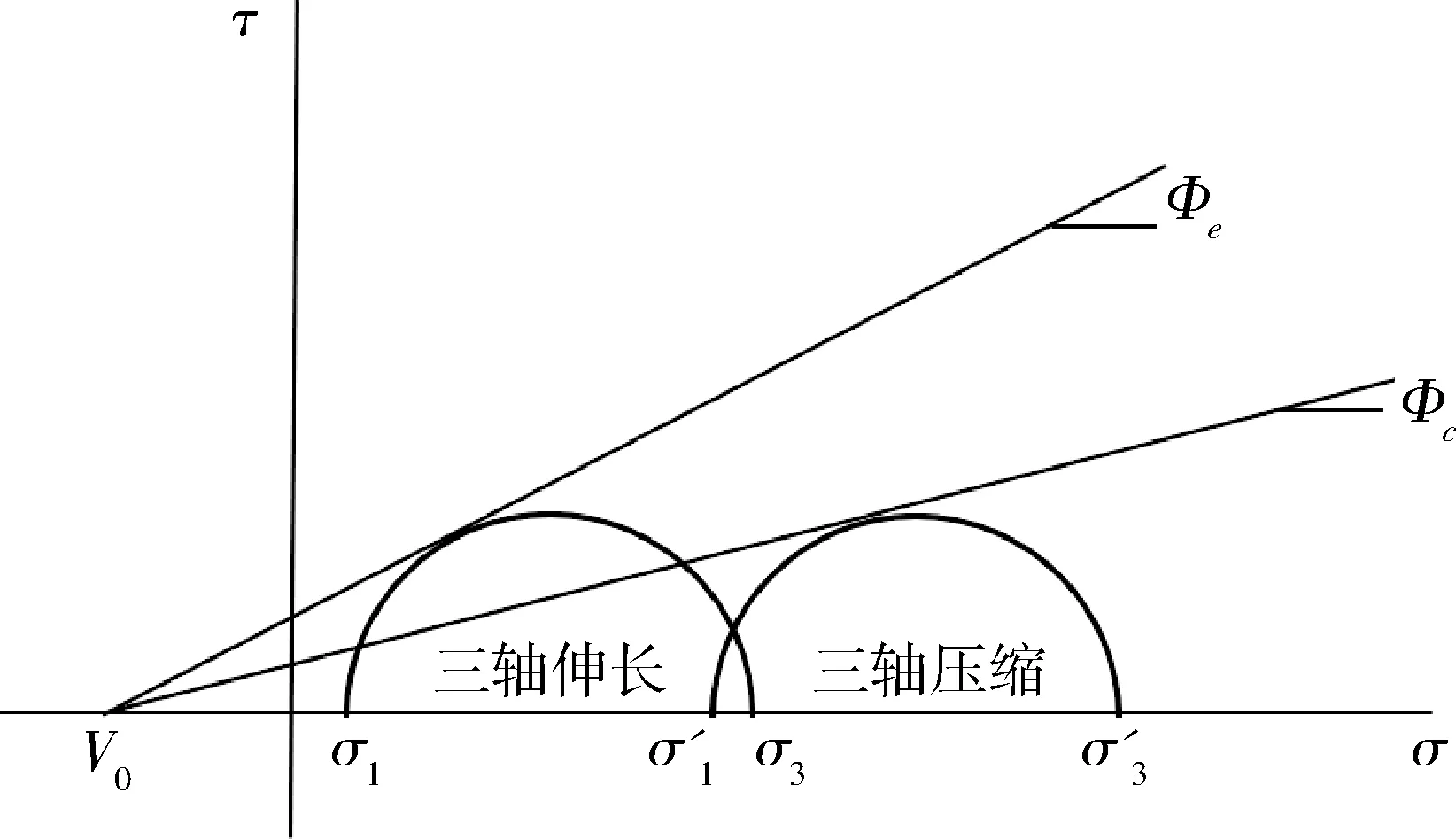
圖1 PMC模型破壞包絡(luò)線Fig.1 PMC model failure envelope

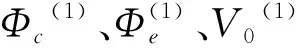
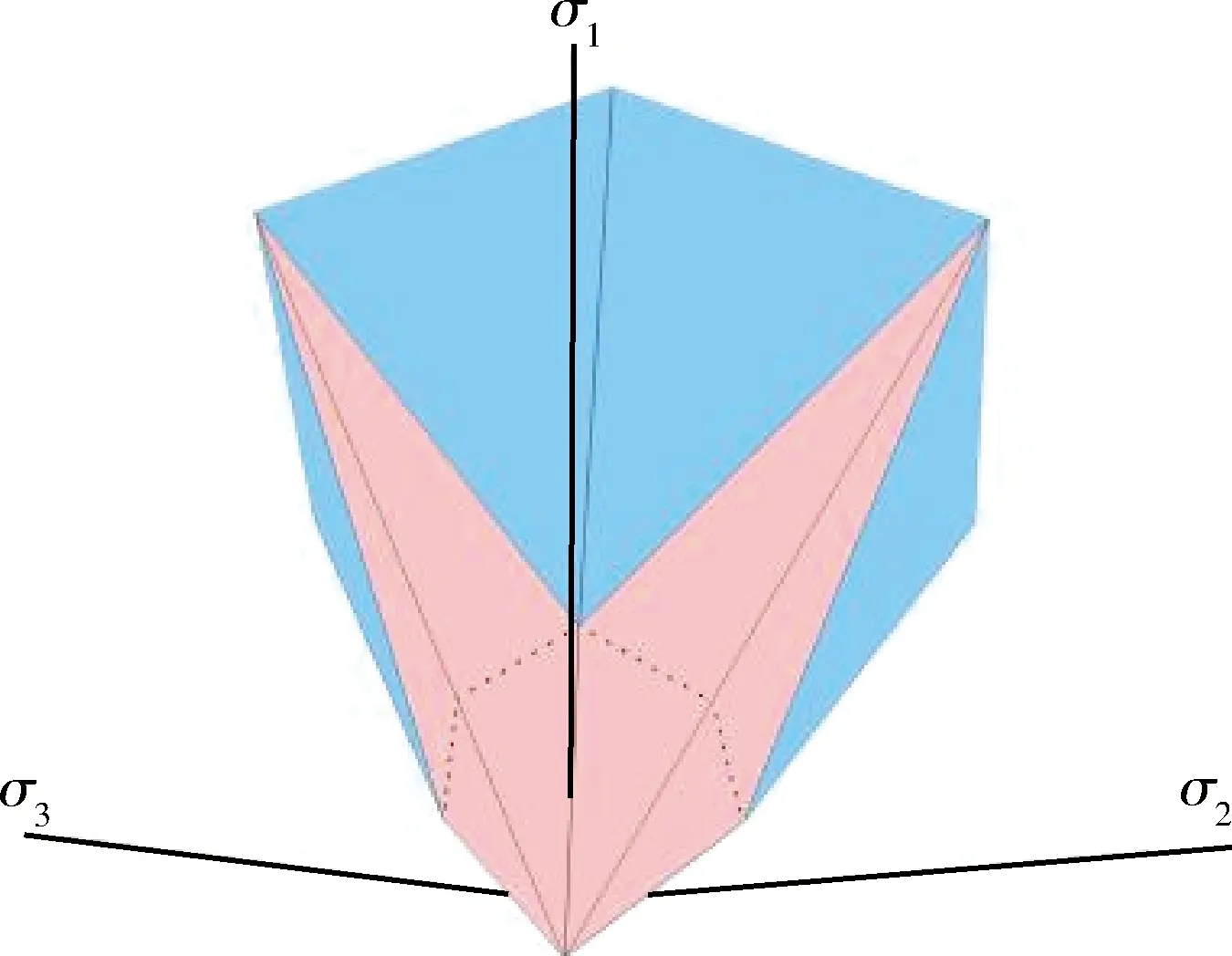
圖2 十二邊形PMC模型Fig.2 Dodecagonal PMC model

2 考慮最大線應(yīng)變強(qiáng)度的三段線強(qiáng)度準(zhǔn)則

2.1 最大線應(yīng)變理論在巖石破壞模式分析中的應(yīng)用

巖石在不同圍壓作用下表現(xiàn)出不同的破壞模式，在拉力作用狀態(tài)或者較低壓力水平下巖石主要以拉破壞為主，而不是以剪破壞為主。然而，無(wú)論是使用MC模型還是PMC模型，都只包含壓縮剪切和純剪切應(yīng)力條件下的破裂準(zhǔn)則，而對(duì)巖石拉伸剪切條件下的破裂準(zhǔn)則沒有表述[7]。因此，采用MC準(zhǔn)則對(duì)拉應(yīng)力或低應(yīng)力水平下巖石破壞進(jìn)行計(jì)算往往會(huì)帶來(lái)較大的誤差。針對(duì)這一現(xiàn)象，PAUL[8]將MC準(zhǔn)則的單斜直線改為一條斜直線和一條與單軸拉伸應(yīng)力圓相切的垂直線，形成雙段線性強(qiáng)度曲線，即拉伸截?cái)鄿?zhǔn)則，截?cái)嗪笃茐臏?zhǔn)則如圖3所示。其中，σt為實(shí)測(cè)抗拉強(qiáng)度，σt0為莫爾強(qiáng)度包絡(luò)線計(jì)算所得的抗拉強(qiáng)度。由圖3可以看出，AB段巖石同時(shí)受到拉應(yīng)力和剪應(yīng)力的作用，此時(shí)其破壞仍以拉破壞為主。然而，十二邊形PMC模型能夠表征巖石材料隨應(yīng)力條件上升由拉斷破壞向剪切破壞轉(zhuǎn)變的機(jī)制，但無(wú)法對(duì)拉伸剪切作用下巖石的破壞機(jī)制進(jìn)行表征。因此，需要對(duì)巖石的拉剪破壞準(zhǔn)則進(jìn)行研究，并獲得其與PMC強(qiáng)度理論的銜接關(guān)系。

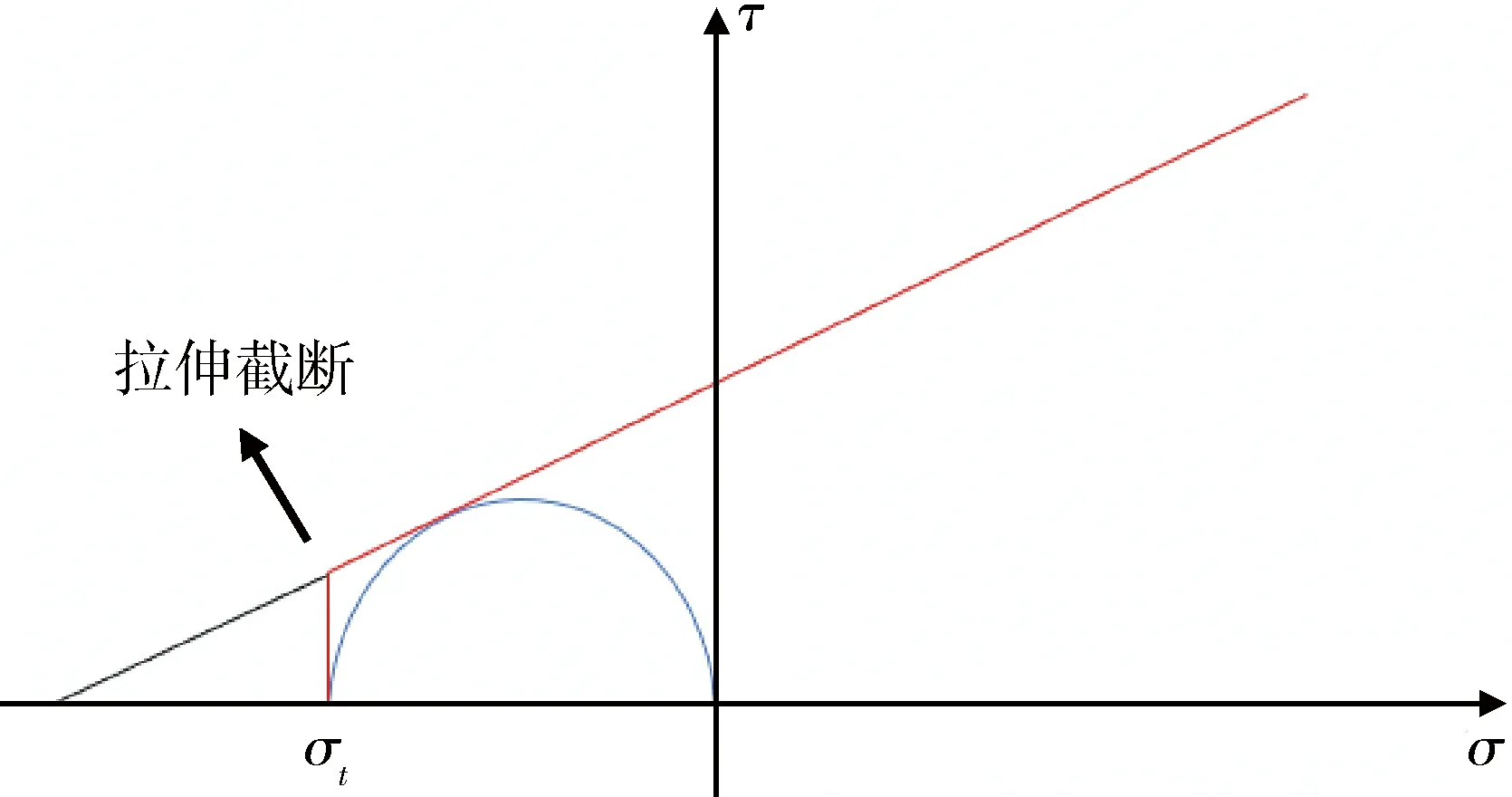
圖3 拉伸截?cái)嗍疽鈭DFig.3 Schematic diagram of stretch truncation

許多學(xué)者對(duì)拉伸剪切條件下巖石的強(qiáng)度準(zhǔn)則進(jìn)行了研究，獲得的模型大致可以分為雙曲線模型[9-12]、拋物線模型[9,11,13]以及基于Hoek-Brown準(zhǔn)則的模型[14-15]。但相對(duì)來(lái)說(shuō)這方面的研究仍然較少，試驗(yàn)數(shù)據(jù)不足，導(dǎo)致目前得出的拉剪本構(gòu)模型與破壞準(zhǔn)則缺乏充分的依據(jù)。STACEY[16]利用最大線應(yīng)變理論試圖預(yù)測(cè)南非深層塊狀石英巖的脆性破壞機(jī)制，研究表明，對(duì)于顯示線性變形行為的材料，破壞發(fā)生可能考慮與拉伸應(yīng)變有關(guān)，巖石的拉伸應(yīng)變可由廣義胡克定律進(jìn)行計(jì)算，見式(6)

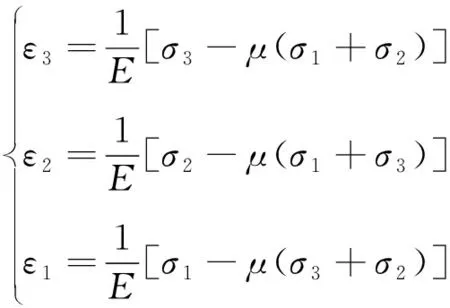
(6)

式中：μ為泊松比；E為彈性模量。根據(jù)最大線應(yīng)變理論，當(dāng)最小主應(yīng)力處的應(yīng)變大于臨界應(yīng)變時(shí)，巖石就會(huì)發(fā)生拉伸破壞。當(dāng)ε3<0時(shí)，試樣發(fā)生拉伸應(yīng)變；當(dāng)ε3>0時(shí)，試樣發(fā)生壓縮應(yīng)變。

2.2 考慮最大線應(yīng)變的三段線性PMC模型的提出

在十二邊形PMC模型的基礎(chǔ)上，添加考慮最大線應(yīng)變理論的破壞面P3，提出同時(shí)考慮拉剪破壞和壓剪破壞的三段強(qiáng)度公式，該模型用三個(gè)主應(yīng)力可以表示為式(7)。

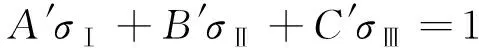
(7)

式中，A′、B′、C′為材料常數(shù)。

對(duì)于破壞面P3(最大線應(yīng)變理論)，根據(jù)廣義胡克定律，可以得到破壞條件見式(8)。

ε1orε2orε3=εc

(8)

式中，εc為臨界應(yīng)變，表達(dá)式見式(9)。

εc=-σt/t

(9)

式中：σt為抗拉強(qiáng)度；μ為泊松比；E為彈性模量。

當(dāng)σⅢ-μ(σⅠ+σⅡ)<0時(shí)，巖石處在拉伸破壞及拉伸破壞至剪切破壞過(guò)渡段。根據(jù)最大線應(yīng)變理論，當(dāng)εⅢ=εc時(shí)，巖石發(fā)生拉伸破壞，符合式(10)。

-σt=σⅢ-μ(σⅠ+σⅡ)

(10)

由式(9)和式(10)可得式(11)。

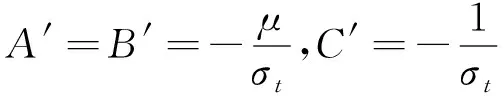
(11)

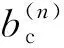
圖4 最大線應(yīng)變理論p-q平面示意圖Fig.4 p-q plane diagram of maximum linear strain theory

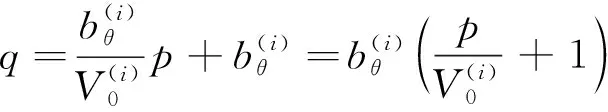
(12)

采用分段線性方式擬合破壞曲線，獲得考慮最大線應(yīng)變的PMC強(qiáng)度公式，在p-q平面內(nèi)，其公式可以表示為式(13)。

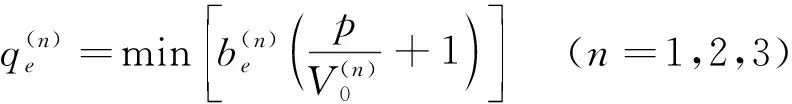
(13)

式中，n為破壞機(jī)制序號(hào)。

當(dāng)n=1時(shí)回歸為常規(guī)PMC模型，n=2時(shí)為十二邊形PMC模型，n=3時(shí)為通用多機(jī)制破壞模式下強(qiáng)度模型。若n=1，且bc=be時(shí)，回歸為常規(guī)Mohr-Coulomb強(qiáng)度公式。

2.3 三段線性PMC模型參數(shù)獲取

ZENG等[5]基于在p-q平面的應(yīng)力不變量關(guān)系的轉(zhuǎn)換提出了一種新的擬合方法。本文基于該方法進(jìn)行三段線性PMC模型參數(shù)獲取方式的推導(dǎo)。在一個(gè)π平面中任何給定的應(yīng)力狀態(tài)都可以在柱坐標(biāo)中(rθ，θ，ρ)表示。圖5為當(dāng)p=0時(shí)，PMC破壞面在π平面中的示意圖。

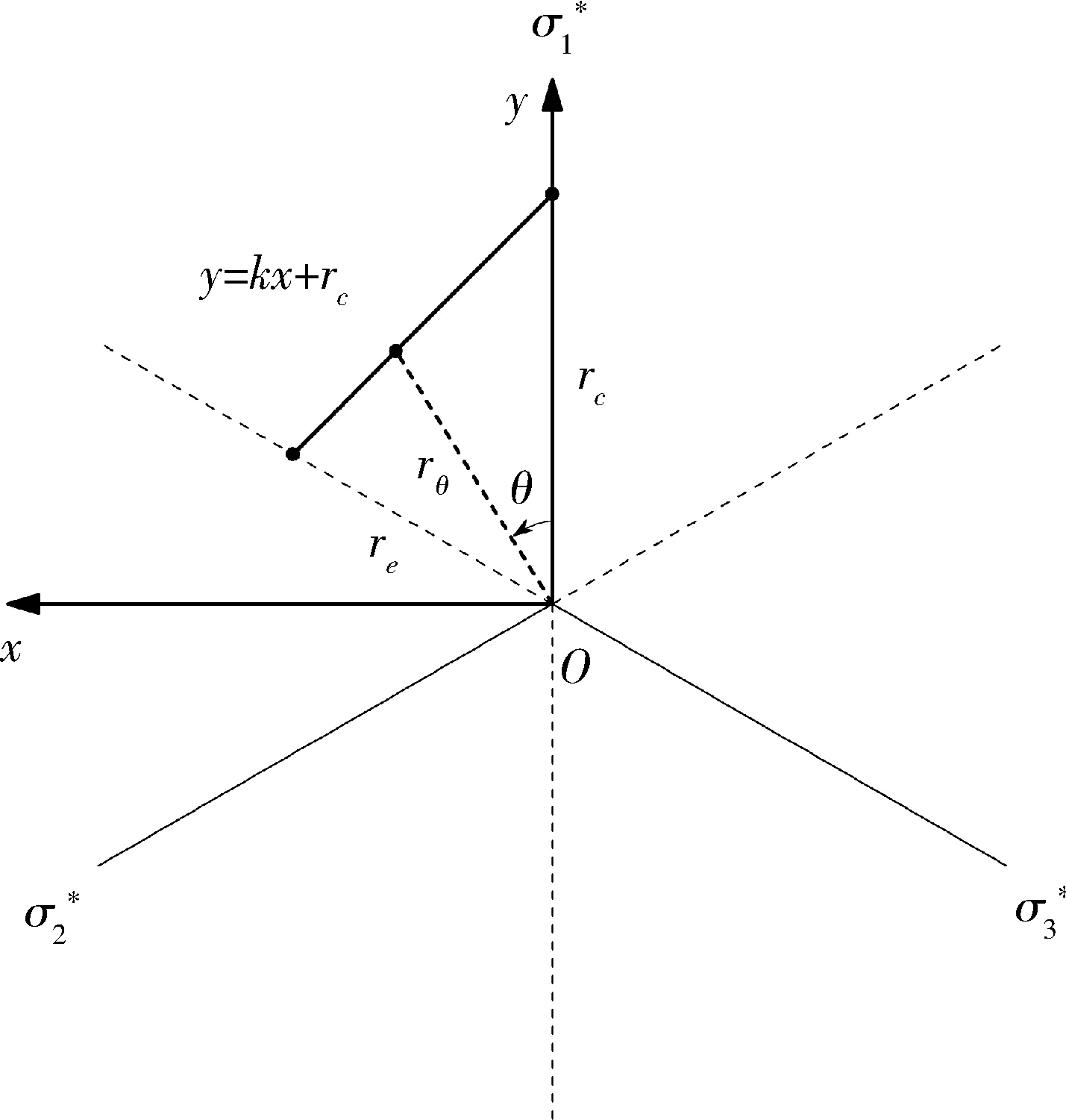
圖5 當(dāng)p=0時(shí)，PMC破壞表面在π平面示意圖Fig.5 Schematic diagram of PMC failure surface inπ plane in polar coordinate and orthogonal coordinate system when p=0

截距bθ需要進(jìn)行定義，bθ和rθ之間建立一種聯(lián)系。破壞包絡(luò)線y=kx+rc在直角坐標(biāo)系中用rθ和θ表達(dá)式見式(14)。

rθcosθ=k×rθsinθ+rc

(14)

在π平面中k是直線的斜率，則rθ見式(15)。

(15)

在任何π平面中，rθ與qθ的關(guān)系可以通過(guò)第二應(yīng)力不變量J2得到式(16)。

(16)

多軸線中qθ=bθ，軸對(duì)稱壓縮線中qθ=bc，軸對(duì)稱伸長(zhǎng)線中qθ=be。因此rθ可以表示為式(17)

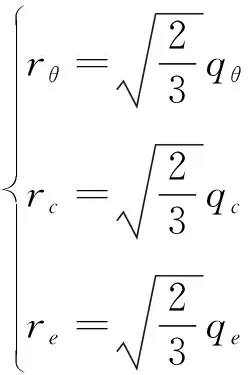
(17)

將式(17)代入式(15)中，可以得到bθ，見式(18)。

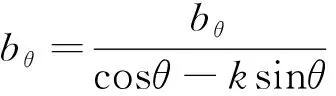
(18)

在p-q平面中，式(18)代表截距bθ的一種函數(shù)關(guān)系，未知變量k需要確定。在π平面中，破壞線經(jīng)過(guò)軸對(duì)稱伸長(zhǎng)點(diǎn)(rθ=re,θ=60°)，式(15)可以表達(dá)為式(19)。

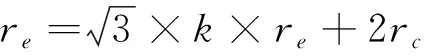
(19)

(20)

將式(20)代入式(19)，可得式(21)。

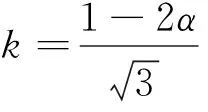
(21)

得知bθ和k的表達(dá)式，p-q平面中PMC準(zhǔn)則的一般方程式(21)可以表達(dá)為式(22)。

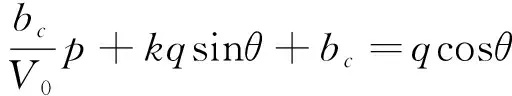
(22)

根據(jù)式(22)，可以使用軸對(duì)稱壓縮、伸長(zhǎng)和多軸測(cè)試數(shù)據(jù)，通過(guò)每種條件下的θ和來(lái)構(gòu)建一個(gè)線性方程組，θ在幾何學(xué)上等于洛德角，但也會(huì)有差異。最初洛德角的定義是從-30°到30°，但是坐標(biāo)系統(tǒng)中是從0°到360°，但是0°到60°已經(jīng)足夠用于各向同性的表達(dá)。θ=0°是軸對(duì)稱壓縮，θ=60°是軸對(duì)稱伸長(zhǎng)，多軸應(yīng)力狀態(tài)的θ值可以通過(guò)主應(yīng)力計(jì)算得到式(23)。

(23)

軸對(duì)稱和多軸條件下強(qiáng)度數(shù)據(jù)表示為(σⅠ,σⅡ,σⅢ)， 帶入式(22)可計(jì)算出每個(gè)應(yīng)力狀態(tài)的p、q、θ，利用這三個(gè)參數(shù)，生成線性方程組A×x=B見式(24)。

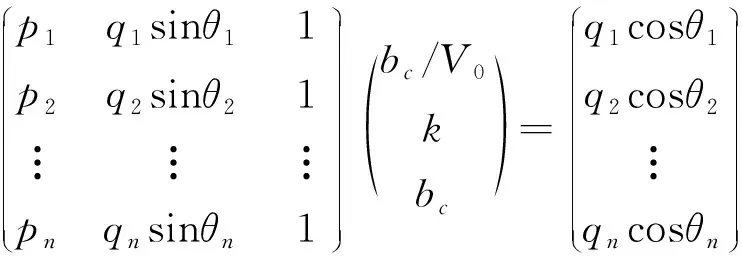
(24)

式中：A為矩形數(shù)據(jù)矩陣；x為參數(shù)向量；B為數(shù)據(jù)向量。

采用最小二乘法求解方程式(24)，獲得bc/V0、k和bc。根據(jù)p-q平面中的軸對(duì)稱壓縮和延長(zhǎng)線的表達(dá)式，求得φc和φe見式(25)。

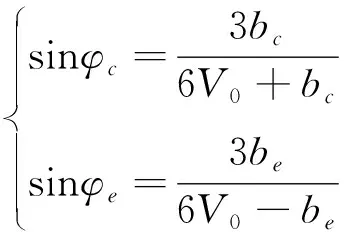
(25)

在p-q平面中，PMC準(zhǔn)則用兩個(gè)內(nèi)摩擦角和頂點(diǎn)V0表示，可以寫為式(26)。

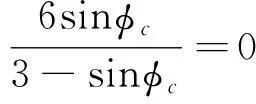
(26)

式中：q為廣義剪應(yīng)力；p為平均應(yīng)力；θ為應(yīng)力洛德角(以最大主應(yīng)力所在軸為0°)；φc為三軸壓縮狀態(tài)下的內(nèi)摩擦角；φe為三軸伸長(zhǎng)狀態(tài)下的內(nèi)摩擦角；V0為三向等拉狀態(tài)下的假設(shè)強(qiáng)度；n為破壞機(jī)制組別(只有剪切破壞時(shí)n=1，考慮拉伸-剪切過(guò)渡段時(shí)n=2，同時(shí)考慮低壓條件下最大線應(yīng)變-過(guò)渡段-剪切應(yīng)變時(shí)n=3)。

3 多重破壞機(jī)制強(qiáng)度的PMC模型試驗(yàn)研究

3.1 試驗(yàn)條件

以四川黃砂巖和金川二礦區(qū)深部花崗巖為試驗(yàn)對(duì)象，采用朝陽(yáng)TAW-2000微機(jī)控制電液伺服巖石三軸試驗(yàn)機(jī)(圖6)和北京科技大學(xué)地應(yīng)力測(cè)量實(shí)驗(yàn)室自主研發(fā)的便攜式自密封巖石三軸試驗(yàn)高壓艙加壓系統(tǒng)(圖6)進(jìn)行高壓三軸壓縮試驗(yàn)。

圖6 試驗(yàn)加載設(shè)備Fig.6 Test loading equipment

花崗巖與砂巖試樣制備參考《水利水電工程巖石試驗(yàn)規(guī)程》(SL 264—2020)中的相關(guān)規(guī)定，制備獲得Φ30 mm×60 mm的標(biāo)準(zhǔn)巖石力學(xué)試件(圖7)。

圖7 制備的巖樣Fig.7 Prepared rock sample

本文中常規(guī)三軸試驗(yàn)依賴兩個(gè)獨(dú)立的加載系統(tǒng)，因此不能利用系統(tǒng)設(shè)置來(lái)進(jìn)行軸壓與圍壓的同時(shí)同速率加載。為保證準(zhǔn)靜態(tài)條件，減小試驗(yàn)誤差，采用軸壓、圍壓分別獨(dú)立的階梯加載方式，階梯加載見表1。試驗(yàn)過(guò)程中軸向加載過(guò)程中先采用應(yīng)力控制，加載速率為100 N/s，當(dāng)加載到靜水壓力狀態(tài)后保持徑向壓力在試驗(yàn)過(guò)程中不變，然后以相同加載速率軸向加載至峰值強(qiáng)度的50%左右切換為變形控制，加載速率為0.03 mm/min。試驗(yàn)中圍壓加載過(guò)程中先采用粗控制，加載速率為1 MPa/s，當(dāng)加載到靜水壓力狀態(tài)前5 MPa后，采用微調(diào)控制手輪進(jìn)行精控制，加載速率為0.2 MPa/s。

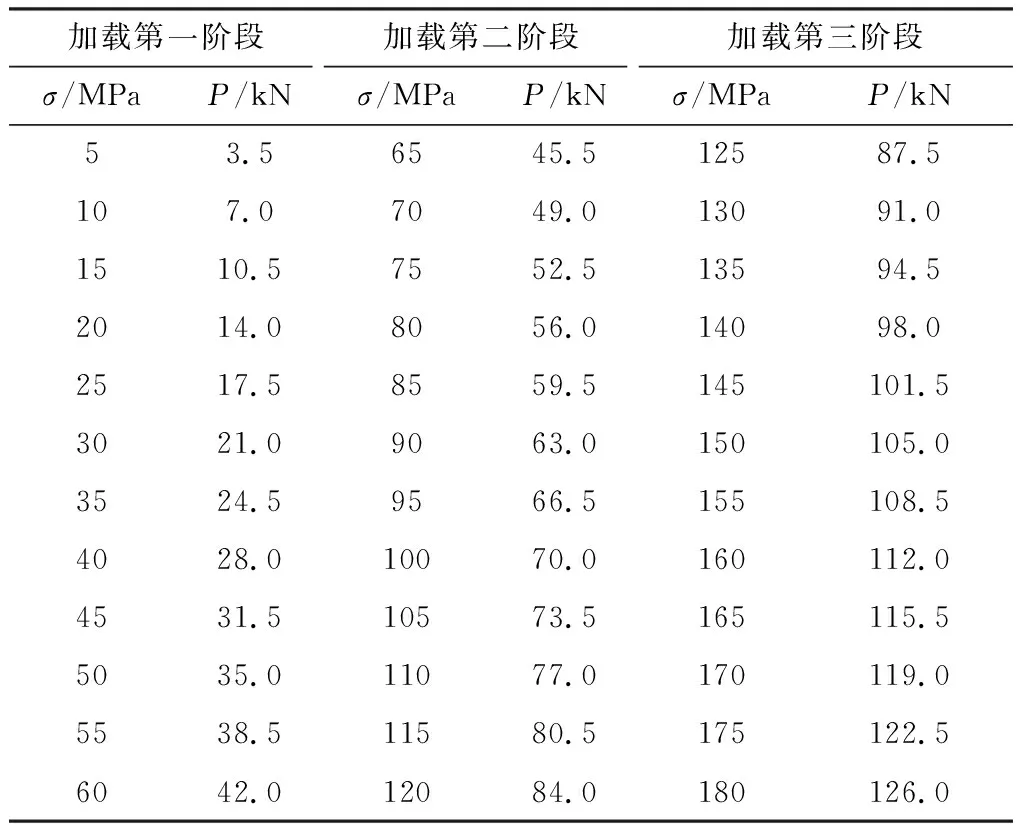
表1 階梯加載軸向荷載與軸向應(yīng)力對(duì)照Table 1 Comparison of axial load and axial stress under step loading

3.2 試驗(yàn)結(jié)果

通過(guò)上述階梯式加載的試驗(yàn)方案對(duì)四川黃砂巖和金川花崗巖進(jìn)行高圍壓常規(guī)三軸試驗(yàn)，其中，四川砂巖三軸壓縮試驗(yàn)在0～170 MPa之間設(shè)置了16組不同的圍壓，金川花崗巖三軸壓縮試驗(yàn)在0～160 MPa設(shè)置了13組不同圍壓。試驗(yàn)過(guò)程中典型的應(yīng)力-應(yīng)變曲線如圖8所示(以部分花崗巖數(shù)據(jù)為例)，試驗(yàn)獲得砂巖和花崗巖峰值強(qiáng)度隨圍壓的變化曲線如圖9所示，試樣破壞形態(tài)如圖10和圖11所示。 由圖8～圖11可以看出，四川黃砂巖與金川花崗巖隨著圍壓增加，其破壞模式表現(xiàn)出相似的規(guī)律：在低圍壓狀態(tài)下破壞時(shí)，以剪切破壞為主，破壞面角度隨著圍壓的增大而呈現(xiàn)減小的趨勢(shì)；在較高圍壓時(shí)，角度依然在變小，慢慢呈現(xiàn)壓剪破壞的趨勢(shì)。

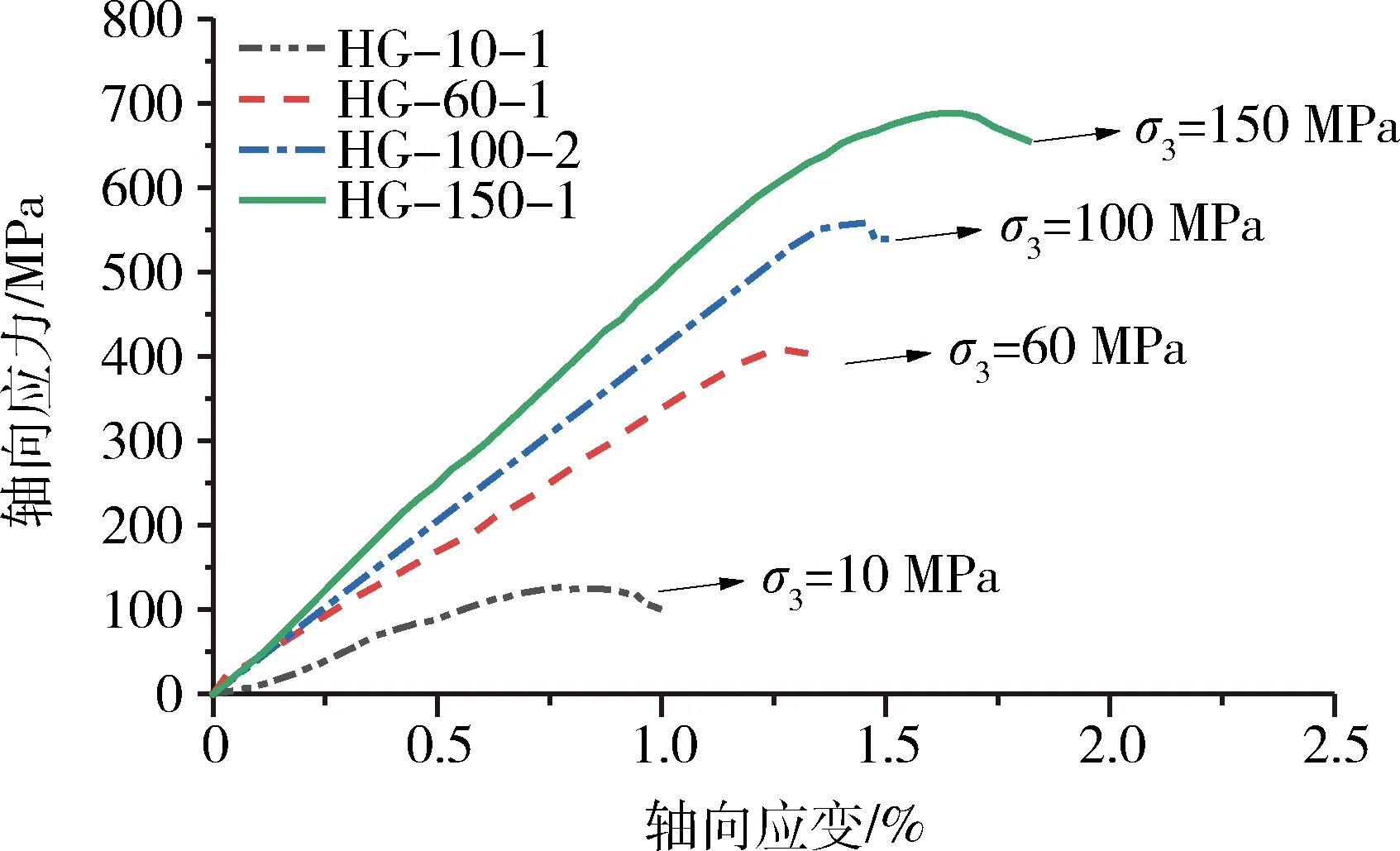
圖8 常規(guī)三軸壓縮試驗(yàn)曲線Fig.8 Conventional triaxial compression test curve

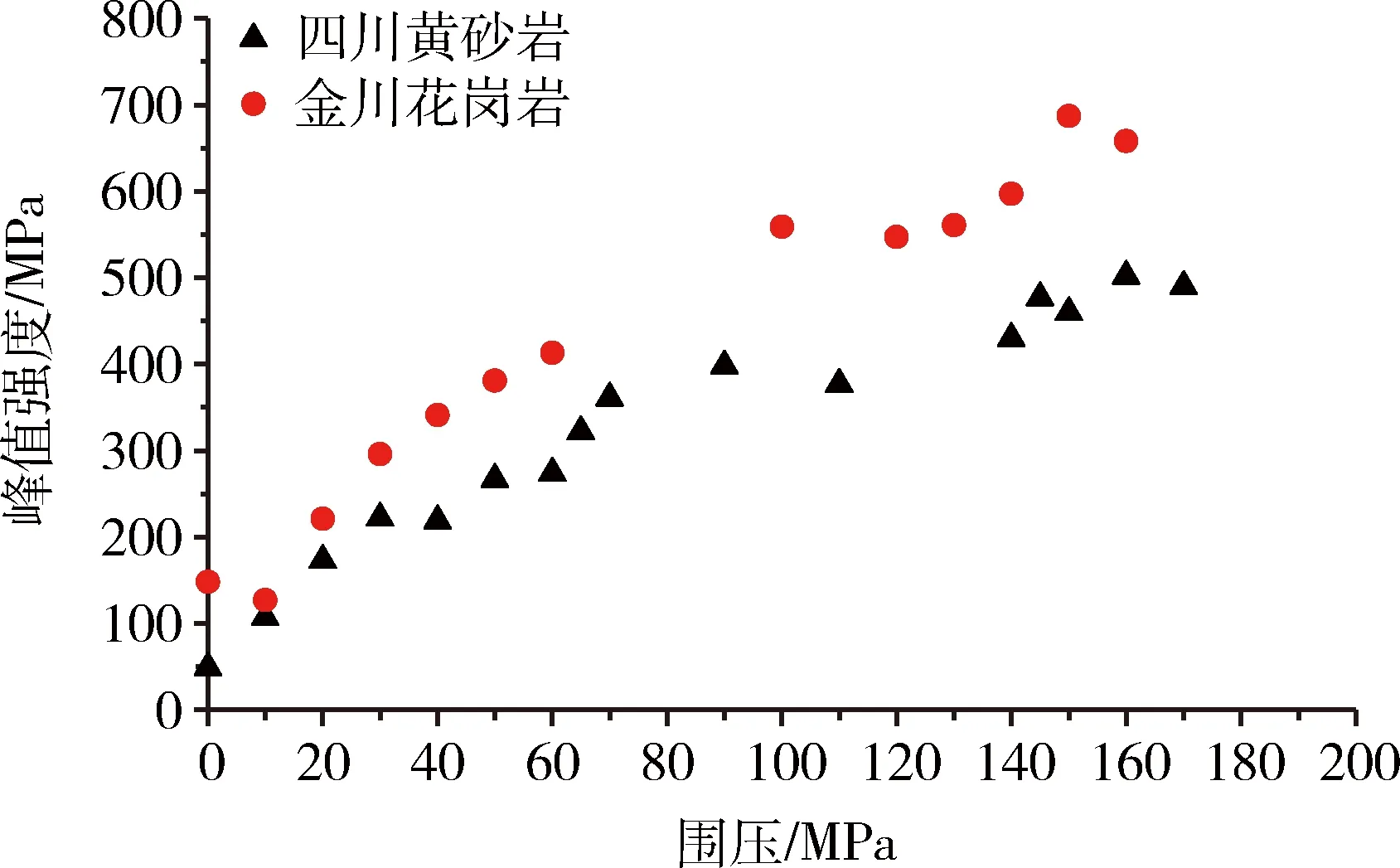
圖9 常規(guī)三軸壓縮試驗(yàn)結(jié)果Fig.9 Results of conventional triaxial compression test

圖10 四川黃砂巖破壞形態(tài)Fig.10 Failure modes of Sichuan yellow sandstone

圖11 金川花崗巖破壞形態(tài)Fig.11 Failure modes of Jinchuan granite

3.3 多重破壞機(jī)制強(qiáng)度的PMC模型適用性驗(yàn)證

1)n=1時(shí)(僅考慮剪應(yīng)力控制段)。以Berea砂巖實(shí)驗(yàn)數(shù)據(jù)進(jìn)行分析，實(shí)驗(yàn)數(shù)據(jù)見表2。圖12為p-q平面中擬合破壞面和實(shí)驗(yàn)數(shù)據(jù)(常規(guī)三軸壓縮實(shí)驗(yàn)和常規(guī)三軸伸長(zhǎng)實(shí)驗(yàn))的對(duì)比圖。q的負(fù)軸表示三軸伸長(zhǎng)實(shí)驗(yàn)，q的正軸表示三軸壓縮實(shí)驗(yàn)，PMC準(zhǔn)則擬合結(jié)果與實(shí)驗(yàn)結(jié)果吻合度較高，且常規(guī)三軸壓縮實(shí)驗(yàn)的摩擦角小于常規(guī)三軸伸長(zhǎng)實(shí)驗(yàn)的摩擦角。φc和φe的差異可說(shuō)明中間主應(yīng)力的影響。

圖12 Berea砂巖實(shí)驗(yàn)數(shù)據(jù)對(duì)比Fig.12 Comparison of experimental data of Berea sandstone

表2 PMC模型擬合結(jié)果數(shù)據(jù)Table 2 PMC model fitting result data

2)n=2時(shí)(考慮拉伸-剪切過(guò)渡段和剪應(yīng)力控制段)。對(duì)金川花崗巖試樣實(shí)驗(yàn)數(shù)據(jù)進(jìn)行分析，為了保證V0(1)≥V0(2)，選擇p≥200 MPa為第一段區(qū)域，p≤200 MPa為第二段區(qū)域進(jìn)行六參數(shù)的PMC模型擬合，擬合結(jié)果見表3。圖13為p-q平面中花崗巖六參數(shù)PMC模型，由圖13可以看出， 花崗巖強(qiáng)度表現(xiàn)出了明顯的分段線性特征，該特征可通過(guò)六參數(shù)PMC模型進(jìn)行擬合。然而，由于缺少三軸拉伸試驗(yàn)數(shù)據(jù)，該模型僅適用于巖石拉伸剪切的過(guò)渡階段，無(wú)法對(duì)花崗巖拉伸破壞模式進(jìn)行表征。

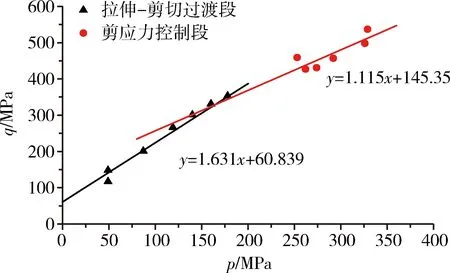
圖13 花崗巖在p-q平面上的六參數(shù)PMC模型Fig.13 Six parameters PMC model of granite on p-q plane

表3 金川花崗巖PMC模型的六個(gè)參數(shù)Table 3 Six parameters of Jinchuan granite PMC model

3)n=3時(shí)(考慮線應(yīng)變控制段-過(guò)渡段-剪應(yīng)力控制段)。對(duì)四川黃砂巖試樣實(shí)驗(yàn)數(shù)據(jù)進(jìn)行分析，擬合結(jié)果見表4。圖14為p-q平面中PMC擬合破壞面和實(shí)驗(yàn)數(shù)據(jù)對(duì)比圖。由圖14可以看出，黃砂巖強(qiáng)度表現(xiàn)出了較為明顯的分段強(qiáng)度特征，此特征符合多重破壞機(jī)制影響下強(qiáng)度規(guī)律。

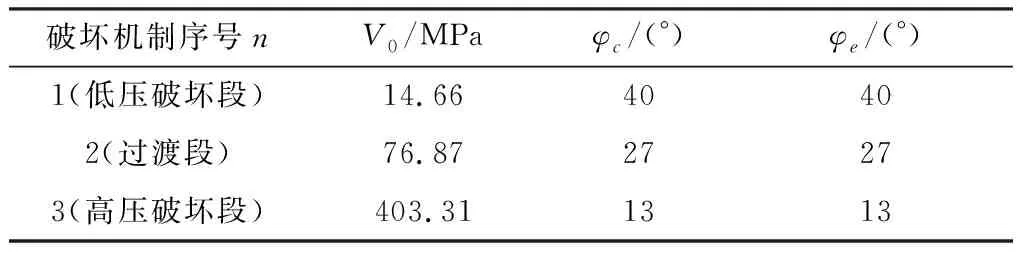
表4 砂巖多破壞機(jī)制影響下強(qiáng)度參數(shù)Table 4 Strength parameters of sandstone under the influence of multiple failure mechanisms

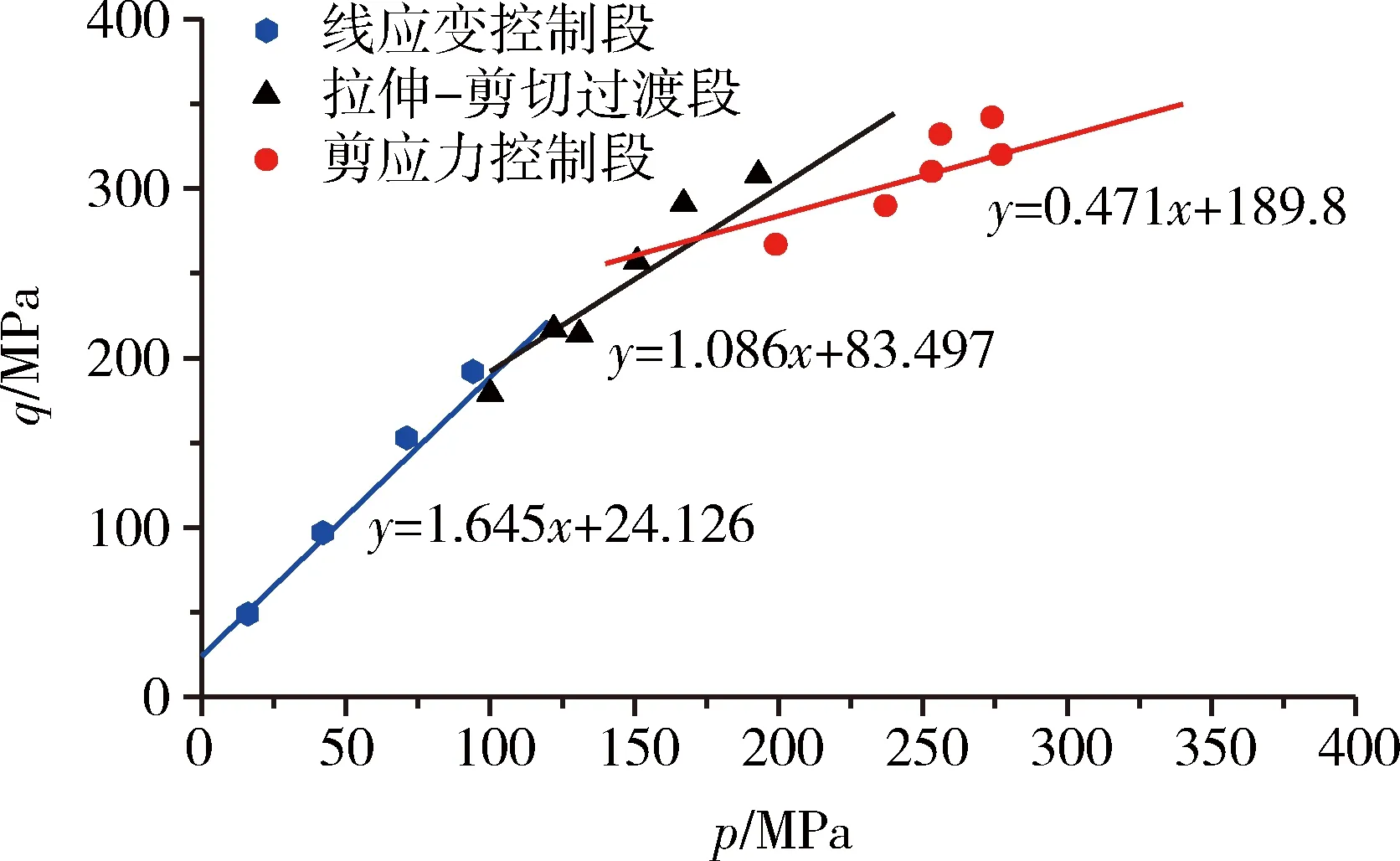
圖14 黃砂巖強(qiáng)度多重機(jī)制破壞強(qiáng)度擬合Fig.14 Fitting of failure strength of yellow sandstone with multiple mechanisms

4 結(jié) 論

1) 基于PMC模型基本原則和最大線應(yīng)變理論，提出了考慮包含最大線應(yīng)變、最大剪應(yīng)力破壞機(jī)制的分段線性強(qiáng)度準(zhǔn)則。該強(qiáng)度準(zhǔn)則考慮線應(yīng)變控制段-過(guò)渡段-剪應(yīng)力控制段三階段強(qiáng)度，每階段由控制性強(qiáng)度線決定強(qiáng)度大小。

2) 為統(tǒng)一表征單獨(dú)破壞機(jī)制、雙重破壞機(jī)制、多重破壞機(jī)制影響下強(qiáng)度過(guò)渡特征和數(shù)學(xué)表達(dá)方式，基于PMC基本強(qiáng)度參數(shù)與π平面應(yīng)力關(guān)系，考慮強(qiáng)度準(zhǔn)則在應(yīng)力空間適用性要求，提出了廣義剪應(yīng)力、平均應(yīng)力及應(yīng)力洛德角為參量的的多破壞機(jī)制影響下強(qiáng)度準(zhǔn)則的不等式統(tǒng)一形式。Mohr-Coulomb準(zhǔn)則、PMC準(zhǔn)則、十二邊形PMC準(zhǔn)則均為其特例。

3) 通過(guò)Berea砂巖、金川花崗巖和四川黃砂巖試驗(yàn)數(shù)據(jù)，分別對(duì)多重破壞機(jī)制PMC強(qiáng)度模型n=1(僅考慮剪應(yīng)力控制段)，n=2(考慮拉伸-剪切過(guò)渡段和剪應(yīng)力控制段)和n=3(考慮線應(yīng)變控制段-過(guò)渡段-剪應(yīng)力控制段)的情況進(jìn)行擬合。 結(jié)果表明，巖石強(qiáng)度表現(xiàn)出了較為明顯的分段強(qiáng)度特征，符合多重破壞機(jī)制影響下強(qiáng)度規(guī)律，從而驗(yàn)證了多重破壞機(jī)制PMC強(qiáng)度模型對(duì)于巖石材料的適用性。