課本題：開展數學探究活動的切入點
——以蘇教版教材《數列》一道習題為例*

徐愛勇 (江蘇省江浦高級中學 211800)

數學教育家弗賴登塔爾曾說：學習數學唯一正確的方法是讓學生進行“再創造”.即數學知識應由學生自己去發現或創造，教師的任務是幫助和引導學生進行“再創造”工作，而不是把現成的知識灌輸給學生，這與新課程所倡導的探究活動的理念是一致的.課本是學生學習的最重要的課程資源，其中的閱讀、思考、探究、例習題等都是編者從學科整體的角度出發，經過精心挑選編寫出來的，符合學生的認知特征，是開展數學探究活動的極好素材.

如《普通高中教科書·數學選擇性必修第一冊》(蘇教版)第四章《數列》第3節習題4.3第13題，筆者以此作為開展數學探究活動的切入點，嘗試從“由已知到已知”“由已知到未知”“由未知到已知”“由未知到未知”等四個方面開展探究，從而達到對“數列求和”的深度學習，努力構建“課堂上如何開展數學探究活動”的操作范式，激發了學生學習數學的興趣.現將筆者的教學實踐過程整理出來，以期拋磚引玉.

問題(蘇教版選擇性必修第一冊第156頁習題4.3第13題)[1]求和：Sn=1+2x+3x2+…+nxn-1.

1 由已知到已知

數學探究活動最原始的形式是“由已知到已知”.所謂“由已知到已知”，是指探究的結果或方法可以直接從已有的結果或方法中得到，最常見的手段就是模仿或類比.

師：我們曾著重研究過等比數列相關問題，同學們還記得等比數列的求和公式是如何推導出來的嗎？

生1(學生回答，教師板演)：利用“錯位相減法”求和！

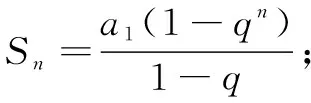
師：很好！再想一想，如何解這道題呢？

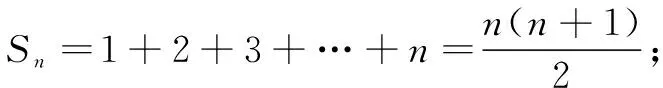
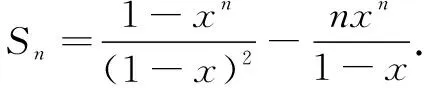
師：能談談你是怎么想到的嗎？

生2(在教師的引導下)：當一個數列的每一項都是一個等差數列與一個等比數列的對應項的積時，可以用“錯位相減法”求和.

師：很好！這是一種“由已知到已知”的數學探究活動,它是在我們能夠識別數列通項結構的基礎上的解題模仿活動.

2 由已知到未知

通常情況下，在利用“錯位相減法”求解完這道題以后，解題探究活動也隨之結束了.雖然學生知道數列求和還有“分組求和”“裂項相消”等方法，但覺得這些方法在這里壓根就用不上，因此也就不會去思考這一問題.此時就進入了數學探究活動的第二層級，即“由已知到未知”.所謂“由已知到未知”是指學生以往掌握的知識或方法在新的條件下不再有效，或者說探究從原有條件下的“已知”變成了新條件下的“未知”問題.這種情況是數學探究活動中經常遇到的現象，面對這種現象往往需要對原有的條件或結論進行變形、推廣、引申，從而產生新結論或新方法.從心理學角度來看，就是通過順應將舊知識適當改變以后再納入新知識的體系當中[2].

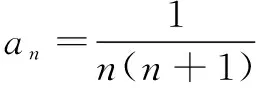
生3：用“裂項相消法”求和！

師：“裂項相消法”本質是把數列的通項分解為另一個數列的相鄰兩項的差，即表示成an=bn-bn-1(n≥2，n∈N*).那么，能否用這種方法來解決這道題呢？

師：不妨先研究這里的特殊情況(課本第156頁第12題)[1]：

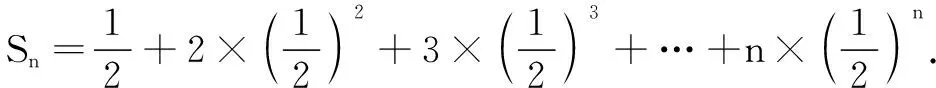
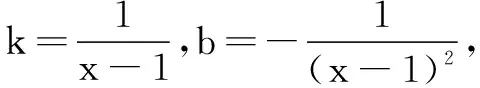
師：這是一種典型的從“已知”到“未知”的探究性學習活動.我們從運算規則的層面考察“錯位相減法”與“裂項相消法”之間的關聯，其實質都是將不規則的運算轉化為規則的運算.

3 由未知到已知

相比“由已知到已知”和“由已知到未知”，數學探究活動中更難的是“由未知到已知”.所謂“由未知到已知”，就是在探究的結論或方法是學生先前未知的情況下探究新的知識.由于學生先前沒有任何這方面的經驗或知識積累，這種探究就更困難，同時也更具有挑戰性.遇到這種情況，往往需要通過對知識內核進行挖掘探究.本節課中，學生通過“錯位相減法”和“裂項相消法”解決本題以后，一般都認為已經很完美了，沒有什么內容再需要探究了.但如果從數學知識的內在本質再去挖掘，我們或許還會有新的發現.這種發現對于學生來說是先前未知的，因此是一種“由未知到已知”的探究活動.

師：我們對數列求和的一些方法進行化歸，將不規則的運算轉化為規則的運算.如果我們能跳出數列的框架束縛，在所學的其他知識板塊中，能否聯想到一些“結構相似點”？

師：這是一次“由未知到已知”的精彩演繹，通過構造函數f(x)=xn，利用導數來解決數列求和問題.這樣的解法太富有創造性了![3]

4 由未知到未知

“由未知到未知”是數學探究活動的最高境界.所謂“由未知到未知”，是指學生在掌握了類比這一探究方法以后，能自覺地尋找探究課題，或將類比方法應用到自己碰到的新問題、新情境當中.比如，本節課學習后，若學生主動探究以下問題，就達到了“由未知到未知”這一最高境界.

問題2(蘇教版選擇性必修第一冊第188頁求導公式8)[1]求函數f(x)=xn的導數.

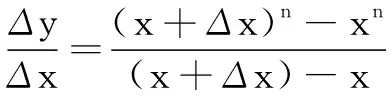
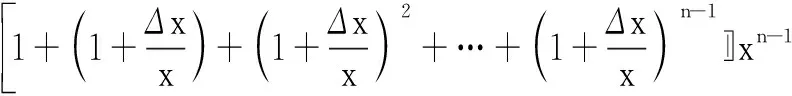
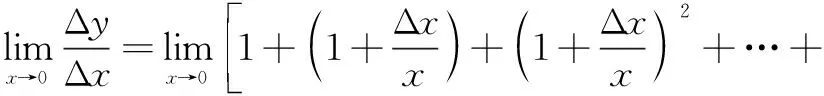
問題3(2007年江蘇高考卷第20題)已知{an}是等差數列，{bn}是公比為q的等比數列，a1=b1，a2=b2≠a1，記Sn為數列{bn}的前n項和.

(1)若bk=am(m,k是大于2的正整數，求證：Sk-1=(m-1)a1.

(2)b3=ai(i是某一正整數)，求證：q是整數，且數列{bn}中每一項都是數列{an}中的項.

(3)是否存在這樣的正數q，使等比數列{bn}中有三項成等差數列？若存在，寫出一個q的值，并加以說明；若不存在，請說明理由.

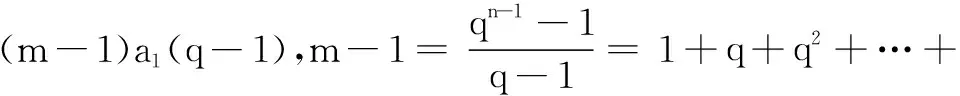
在開展數學探究活動時，設置的問題應來源于課本且高于課本，應整體設計、分步實施探究活動，以實現“已知與未知”之間的轉換，引導學生從類比模仿到自主創新、從局部實施到整體構想，積累發現和提出問題、分析和解決問題的經驗，養成獨立思考與合作交流的習慣[4].