面向移動終端的密文可驗證屬性基可搜索加密方案*

牛淑芬,張美玲,周思瑋,閆 森

(西北師范大學計算機科學與工程學院，甘肅 蘭州 730070)

1 引言

隨著云計算[1]的發展和輕量級設備的出現，大多數個人和企業選擇將數據存儲到云服務器上以便管理。由于云服務器不完全可信，存儲在云上的數據存在被攻擊或隱私泄露的風險，因此在將數據存儲到云服務器上之前必需先加密。在查找數據時，需先從云服務器上將需要的數據下載到本地再解密，這樣的數據使用方式會耗費大量的網絡帶寬，并且搜索效率低下。

為了提高密文檢索的效率，Song等人[2]首次提出對稱可搜索加密SSE(Symmetric Search Encryption)方案。該方案通信量低，但計算開銷隨著查詢規模增大而增大。為了解決這個問題，Boneh等人[3]提出了帶關鍵詞搜索的公鑰加密方案PEKS (Public key Encryption with Keyword Search)。數據擁有者用公鑰加密數據并上傳到云服務器，僅對應的私鑰生成陷門上傳到云服務器才能搜索加密數據。近年來，可搜索加密已成為研究熱點[4 - 7]，可搜索加密SE(Searchable Encrption)具有許多搜索特征，如單/多關鍵詞可搜索、模糊關鍵詞搜索、可驗證關鍵詞搜索、排序關鍵詞搜索等。由于單關鍵詞檢索的缺陷，Golle等人[8]首次提出了多關鍵詞搜索方案，但關鍵詞陷門大小隨著加密文檔數量增加而增加。Wu等人[9]為了加強對用戶的訪問控制，提出了一種高效的支持多用戶訪問控制MMSE(Multi-keyword Searchable Encryption supporting Multi-user access control)的多關鍵詞可搜索加密方案。

隨著科技的高速發展，移動終端(如智能手機、平板、無線可穿戴設備等)基本全面覆蓋了生活，由于有限的計算資源、存儲空間、通信帶寬及電池容量等的限制，數據交互的效率較低。將云計算與其結合，通過移動云存儲，移動終端用戶將數據存儲在云服務器上并且可以便捷地共享數據。為防止云服務器上的隱私數據被惡意竊取和攻擊，數據擁有者通常在將數據存儲到云服務器上之前會對其加密。傳統的加密方法能夠保證數據的安全性，但不能夠對數據進行靈活的訪問控制。Sahai等人[10]首次提出了屬性基加密ABE (Attributed-Based Encryption)方案，同時實現了數據的安全性和靈活訪問控制[11,12]。用戶的屬性隨著系統用戶變化而變化，為了撤銷無關屬性，傳統的屬性撤銷機制通過重加密用戶的密鑰來實現用戶屬性的更新[13 - 15]。Wang等人[16]提出了一種多數據所有者可撤銷和可搜索的屬性基加密方案，使用相同的訪問策略加密索引和消息。由于云服務器誠實且好奇的特點，對云服務器返回的數據進行驗證是很有必要的。文獻[17,18]提出了支持多關鍵詞可搜索且可驗證的屬性基加密方案，文獻[17]不支持用戶可變屬性的更新，文獻[18]實現的細粒度訪問控制保證了數據的私密性，支持用戶的屬性撤銷。Sun等人[19]提出了云存儲中數據可驗證的屬性基多關鍵詞可搜索方案，允許數據用戶對云服務器的搜索結果進行正確性驗證，同時支持數據用戶屬性撤銷與更新。

現有的大多數方案中，數據搜索結果是由云服務器返回的，由于它不完全可信，可能會獲得偽造或篡改后的數據。用戶收到搜索結果后需要對密文數據進行驗證和解密，這極大地增加了用戶的計算量。此外，系統中用戶屬性隨時會發生變化，應及時對用戶過期的屬性進行更新。因此，針對上述問題，本文提出了面向移動終端的密文可驗證屬性基可搜索加密方案，數據屬主將加密后的密文數據和代表身份的簽名一起存儲至云服務器；移動終端用戶生成搜索陷門上傳到云服務器后，由云服務器進行檢索；引入一個可信第三方，由其驗證云服務器返回的搜索結果的正確性和完整性；可信第三方使用移動終端用戶盲化后的私鑰，進行部分解密工作。為了更好地管理用戶屬性，使用屬性撤銷方法，在不影響用戶的前提下，更新已發生變化的用戶屬性及其相關的密鑰和密文。

2 預備知識

2.1 雙線性映射

設p是一個大素數，G1和G2是2個階為p的群。g是群G1的一個生成元，定義一個雙線性映射e:G1×G1→G2,雙線性映射滿足下面的性質：(1)雙線性。對于任意的a,b∈Zp,有e(ga,gb)=e(g,g)ab。(2)非退化性。e(g,g)≠1。(3)可計算性。G存在一個有效算法計算e(g,g)。

2.2 訪問結構

令P={P1,P2,…,Pn}是一個n元集合。對于任意集合B，C，如果B∈AJ且B?C，則C∈AJ，那么本文稱集合AJ?2P是單調的。如果集合AJ是2P的一個非空子集，那么AJ是一個訪問結構。包含在集合AJ中的子集稱為AJ的授權集合，反之稱為AJ的非授權集合。

2.3 線性秘密共享方案LSSS(Linear Secret- Sharing Scheme)

設(Μ,ρ)表示訪問策略A，其中，Μ是l行n列的秘密生成矩陣。對于1≤i≤l，ρ(i)是映射Μ的第i行的映射函數，代表不同的屬性。線性秘密共享滿足下面的條件：

(1)令s∈Zp為一個秘密值，隨機選擇r2,…,rn∈Zp，列向量v=(s,r2,…,rn)，然后計算λi=(M·v)i，其中λi是屬性ρ(i)的子秘密值。

(2)令S∈A為授權集合，定義I={i:ρ(i)∈S}，I?{1,2,…,l}。存在{ωi∈Zp}i∈I滿足∑i∈IωiΜi=(1,0,…,0)。其中Mi表示M中第i行的向量。由∑i∈Iωiλi=s恢復秘密值，可以在多項式時間內找到這些常數{ωi}。

2.4 通用雙線性群

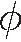
2.5 困難問題假設

判定性并行雙線性指數假設q-BDHE(q- parallel Bilinear Diffie-HEllman)：是指不存在多項式時間的算法以不可忽略的優勢判定R=e(g,g)aq+1s是否成立。

隨機選取a,s,b1,…,bq∈Zp，g是G的生成元。給出如式(1)所示的y:

y=(g,gs,ga,…,gaq,gaq+2,…,ga2q,

?1≤j≤qgsbj,ga/bj,…,gaq/bj,gaq+2/bj,…,ga2q/bj,

?1≤k,j≤q,k≠jgasbk/bj,…,gaqsbk/bj)

(1)

很難從一個隨機元素R∈GT中區分出一個有效元組e(g,g)aq+1s∈GT。算法B返回z∈{0,1}，在群G上若|Pr[B(y,e(g,g)aq+1s)=0]-Pr[B(y,R)]|≥ε，則能以優勢ε解決q-BDHE困難問題。

3 系統模型和安全模型

3.1 系統模型

本文方案包括5個實體，即云服務器CS(Cloud Server)、可信第三方TTP(Trusted Third Party)、屬性授權中心AA(Attributed Authority)、數據屬主DO(Data Owners)和移動終端用戶DU(Data Users)。系統模型如圖1所示。

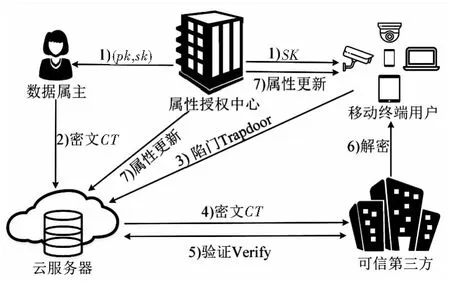
Figure 1 System model圖1 系統模型

(1)云服務器。負責數據存儲與計算;執行陷門與密文匹配操作，若匹配成功，則返回正確密文給可信第三方；屬性撤銷階段更新相應的密文。

(2)可信第三方。驗證云服務器返回的密文結果是否完全正確。

(3)屬性授權中心。是完全可信實體，負責系統的初始化、數據用戶的注冊及動態屬性撤銷。

(4)數據屬主。從文件中提取關鍵詞，生成關鍵詞索引并且使用對稱密鑰加密文件。同時，使用自己定義的訪問控制策略加密對稱密鑰，最后將所有密文上傳至云服務器。

(5)移動終端用戶。使用私鑰生成陷門上傳至云服務器然后搜索密文。收到可信第三方發送的密文，且用戶屬性滿足訪問策略，則解密密文。

3.2 方案形式化定義

本文方案包括7個階段：系統建立、密鑰生成、數據加密、關鍵詞搜索、密文驗證、密文解密和屬性撤銷。表1給出了本文中部分符號的描述。

Table 1 Symbols description

(1)系統建立，Setup(1K)→(PK,MK)：該算法由屬性授權中心執行。給定安全參數K，輸出系統公共參數par、系統公鑰PK和主密鑰MK。

(2)密鑰生成,KeyGen(MK,Suid)→{SKu,(pko,sko)}：該算法由屬性授權中心執行。輸入主密鑰MK和數據用戶的屬性集Suid，輸出移動終端用戶的私鑰SKu和數據屬主的公私鑰對(pko,sko)。

(3)數據加密:該算法由數據屬主執行。首先，執行索引生成算法IndexGen(PK,W)→IW：輸入系統公鑰PK和關鍵詞集W，輸出關鍵詞的索引IW；其次，執行加密算法Encrypt(PK,kθ,(M,ρ))→CT：輸入系統公鑰PK、對稱密鑰kθ和訪問策略(M,ρ)，輸出密文集合CT，根據文件的身份生成簽名sigθ。

(4)關鍵詞搜索。首先，用戶執行陷門生成算法Trapdoor(PK,W′,SKu)→TW′：輸入PK，搜索關鍵詞集W′和私鑰SKu，生成搜索陷門TW′;其次，云服務器執行搜索算法Search(TW′,IW)：輸入陷門TW′和索引IW，驗證它們是否匹配。若匹配，則將搜索結果發送給可信第三方,否則終止算法。

(5)密文驗證,Verify(sigθ,Cθ,PK,pko)：該算法由可信第三方執行。收到云服務器返回的密文后，可信第三方與云服務器交互驗證密文的正確性。驗證通過，可信第三方對密文進行部分解密，并將解密后的密文發送給用戶。

(6)密文解密。若驗證通過，用戶向可信第三方發送盲化密鑰BSKu，可信第三方執行解密算法Decrypt(BSKu,CT′,Cθ)：輸入盲化密鑰和密文，計算A=e(g,g)atzs，根據盲化的密鑰Dz和密文C1再計算T=e(Dz,C1)。將(A,T)發送給移動終端用戶，用戶計算得到對稱密鑰kθ。

(7)屬性撤銷。可信第三方執行屬性密鑰更新算法，輸入撤銷屬性x′，利用屬性更新密鑰AUKx′更新屬性公鑰PAK；移動終端用戶執行私鑰更新算法，輸入私鑰SKu和屬性更新密鑰AUKx′，對已變屬性的私鑰進行更新；密文更新算法由云服務器執行，輸入撤銷屬性x′和屬性更新密鑰AUKx′，對已變屬性的密文進行相應更新。

3.3 安全模型

本文通過在敵手A和挑戰者B之間定義2個安全游戲證明方案的安全性。

(1)游戲Ⅰ:IND-CKA。

初始階段：挑戰者C執行系統建立算法Setup(1K)生成系統公鑰PK和主密鑰MK，并將PK發送給A，自己保存MK。

階段1A可以對以下詢問進行多項式次數的查詢。C令LW為初值是空值的關鍵詞集合。

KeyGen Oracle：輸入系統公鑰PK和主密鑰MK，挑戰者C執行密鑰生成算法KeyGen，將私鑰SKu發送給敵手A。

Trapdoor Oracle：輸入系統公鑰PK、私鑰SKu和詢問關鍵詞集合W*，挑戰者C執行陷門生成算法Trapdoor，將陷門TW*發送給敵手A。

挑戰：敵手A發送等長的2條消息m0和m1給挑戰者C，m0和m1之前未被詢問過。挑戰者C隨機選擇b∈{0,1}，生成關鍵詞集合Wb的索引IWb，并將其發送給敵手A。敵手A不能從陷門詢問中得到任何關于消息m0和m1的信息。

階段2與階段1詢問方式相同。詢問過的消息m0和m1不能被重復詢問。

猜測：敵手A生成一個猜測b′∈{0,1}，若b′=b，則敵手A贏得游戲Ⅰ。

(2)游戲Ⅱ：IND-sCP-CPA。

初始階段：A選擇一個訪問結構A*，C執行系統建立算法Setup(1K)生成系統公鑰PK和主密鑰MK，并將PK發送給A，自己保存MK。

階段1此階段敵手A可以對以下詢問進行多項式次數的查詢。

KeyGen Oracle：敵手A提交元組(uid,Suid)對私鑰SKu進行查詢，其中屬性集Suid與訪問結構A*不匹配。

RePAKOracle：給定任意一個屬性x′，敵手A能夠對屬性更新密鑰AUKx′進行查詢。

挑戰：敵手A發送等長的2條消息kθ0和kθ1給挑戰者C。C隨機選擇b∈{0,1}，利用訪問結構A*加密kθb，最后將密文CT′*發送給敵手A。

階段2與階段1詢問方式相同。

猜測：敵手A生成一個猜測b′∈{0,1}，若b′=b，則敵手A贏得游戲Ⅱ。

4 具體方案

4.1 具體方案

面向移動終端的密文可驗證屬性基可搜索加密方案具體如下所示：

階段1系統初始化。

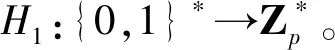
階段2密鑰生成。

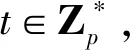
階段3數據加密。

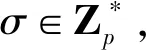
(2)DO使用對稱密鑰kθ加密文件Fθ，得到加密文件Cθ=Enckθ(Fθ)。Encrypt(PK,kθ,(Μ,ρ))→CT：輸入PK、kθ和訪問策略(Μ,ρ)，Μ是l×n的矩陣，函數ρ映射Μ中每一行不同的屬性。選擇隨機值y2,…,yn∈Zp，令向量v=(s,y2,…,yn)。通過λi=Μi·v(1≤i≤l)可以計算出秘密值s，Μi表示Μ中第i行的向量。算法隨機選擇r1,…,rl∈Zp，計算密文,如式(2)所示:

CT′={(Μ,ρ),C0=kθ·e(g,g)βs,C1=gs,

?i∈1,…,l:C2i=gaλi·H(ρ(i))ri,

C3i=(gvρ(i))ri}

(2)

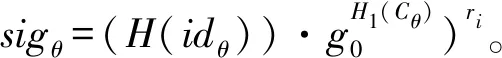
階段4關鍵詞搜索。

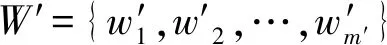
(2)Search(TW′,IW):CS收到來自DU的搜索陷門TW′后，通過驗證如式(3)所示的等式判斷關鍵詞索引IW與搜索陷門TW′是否匹配：

(3)

若匹配成功，CS將密文CT=(IW,Cθ,CT′)發送給TTP；否則，算法終止。

階段5密文驗證。

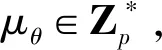
階段6密文解密。

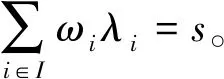
(gβz·gatz,gtz,gaαz,H(x)tz/vx)

(4)

階段7屬性撤銷。

當數據用戶要撤銷屬性x′時，AA將移動終端用戶的身份加入屬性撤銷列表RLx′中。

(2)ReKey(SKu,AUKx′)→SK′u：由DU執行該算法，輸入SKu和AUKx′，計算更新后的私鑰,如式(5)所示:

(5)

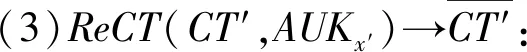
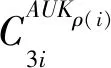
4.2 正確性證明

(1)搜索階段。

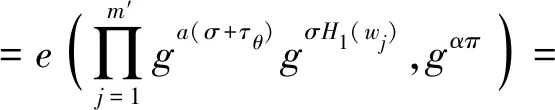
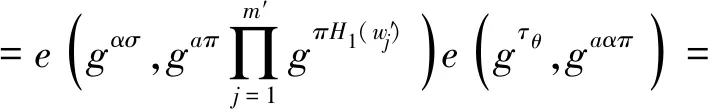
(2)驗證階段。

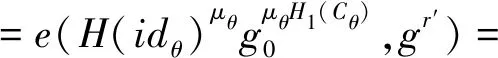
e(ξ,g)

(3)解密階段。

e(g,g)atzs

T=e(gβz·gatz,gs)=e(gβz,gs)e(gatz,gs)=

e(g,g)βzse(g,g)atzs

kθ=Kz-1

5 安全性證明

定理1給定一個單向哈希函數H1，在通用雙線性群模型下，本文方案是抵抗不可區分的選擇關鍵詞攻擊IND-CKA。

證明敵手A在不可區分選擇關鍵詞攻擊游戲中要區分ga(σ+τθ)gσH1(W0)和ga(σ+τθ)gσH1(W1)。輸入f∈Zp，A能夠區分gf和ga(σ+τθ)gσH1(W0)的優勢等同于區分gf和ga(σ+τθ)gσH1(W1)的優勢。本文假設A能夠區分gf和ga(σ+τθ)，游戲描述如下:

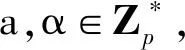
階段1A進行私鑰和陷門詢問。

KeyGen Oracle：C計算D″=gaα，PK=(g,ga,gα)，并將D″發送給A。

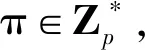
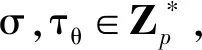
階段2與階段1相同，已被詢問過的關鍵詞集合W0和W1不再進行陷門詢問。如果A根據gh′詢問返回的信息可以構造gh′a(σ+τθ)，就可以區分gf和ga(σ+τθ)。本文還需要證明A在不可區分的選擇關鍵詞攻擊游戲中以不可忽略的優勢不能區分gh′和e(g,g)h′a(σ+τθ)。因為只能從ασ中獲得σ,要想得到e(g,g)h′a(σ+τθ)，h′中應該含有α。然而，α只有C擁有，所以A任何時候都不能得到e(g,g)h′a(σ+τθ)。從而證明A不能區分gf和ga(σ+τθ)，即不能區分ga(σ+τθ)·gσH1(W0)和ga(σ+τθ)·gσH1(W1)，也就是A不能以一個不可忽略的優勢攻破不可區分的選擇關鍵詞攻擊游戲。

□

定理2若q-BDHE假設成立，則本文方案抵抗選擇性不可區分的密文策略和選擇明文攻擊IND-sCP-CPA。

證明假設敵手A能夠在選擇的安全模型下以不可忽略的優勢ε攻擊本文方案，令模擬器B以不可忽略的優勢ε/2解決q-BDHE問題。挑戰者C選擇生成元為g的群G1，雙線性映射e:G1×G1→GT。C隨機選取a,s,b1,…,bq∈Zp，令y如式(6)所示:

y=(g,gs,ga,…,gaq,gaq+2,…,ga2q,

?1≤j≤qgsbj,ga/bj,…,gaq/bj,gaq+2/bj,…,ga2q/bj,

?1≤k,j≤q,k≠jgasbk/bj,…,gaqsbk/bj)

(6)

隨機選取μ∈{0,1}，若μ=0，C令T=e(g,g)aq+1s;若μ=1，則C選擇群GT中的一個隨機元素T。

初始化：B收到q-BDHE的挑戰信息(y,T)后，A產生一個挑戰訪問結構(Μ*,ρ*)，Μ*是l*×n*的矩陣。

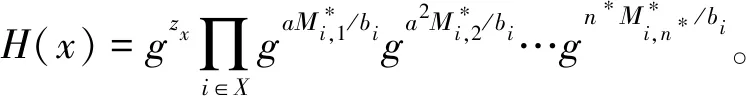
階段1B設置列表LSKu為三元組(uid,Suid,SKu)，初始值為空。A在多項式時間內可以進行以下詢問：

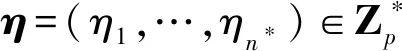
t=r+η1aq+η2aq-1+…+ηn*aq+1-n*

(7)

H(x)t/vx

(8)

最后，B將私鑰SKu={D,D′,{Dx}x∈Suid}加入列表LSKu并發送給A。

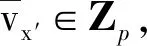
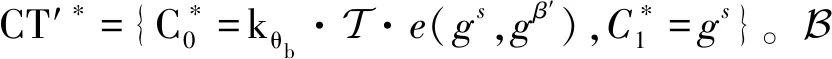
(9)

(10)

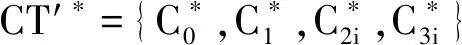
階段2與階段1的詢問方式相同。

猜測：A輸出一個猜測b′∈{0,1},若b′=b，則B返回ν′=0，T=e(g,g)aq+1s；否則，B返回ν′=1，T為群GT中的一個隨機元素。該游戲中A定義的優勢為ε。如果ν=0，A將會獲得一個有效密文，則Pr[b′=b|ν=0]=0.5+ε。因為當b′=b時，B返回ν′=0，則有Pr[ν′=ν|ν=0]=0.5+ε。如果ν=1時，A無法得到關于b的有效信息，則有Pr[b′=b|ν=1]=0.5。當b′≠b時，B返回ν′=1時，則有Pr[ν′=ν|ν=1]=0.5。因此，B解決判定性假設q-BDHE問題的優勢為：

□

6 性能分析

6.1 功能特性比較

表2將本文方案與文獻[17，18]方案進行了對比，其中主要有訪問控制樹和線性秘密共享2種訪問策略。表2表明，本文方案在功能特性上具有一定優勢。

Table 2 Function comparison

6.2 計算量比較

本節從理論角度分析了本文方案與文獻[17，18]方案在計算開銷方面的優勢。首先設雙線性映射配對時間為Tp，指數運算時間為Te，乘法運算時間為Tm，哈希函數運算時間為Th。在表3和表4中，|Au|表示用戶的屬性集合，|Xf|表示訪問樹的葉子節點集合，|W|表示文件的關鍵詞集合，|M|表示滿足訪問策略的最小屬性集。由表3可以看出，在密文生成階段，由于文獻[18]有多個配對運算，故本階段各方案計算量由大到小依次為文獻[18]方案、本文方案和文獻[17]方案;在陷門生成階段，本文方案無配對運算，且指數運算和乘法運算都少于文獻[17，18]的，故在本階段本文方案的計算效率最優；在搜索階段，文獻[17]方案的配對運算遠遠大于文獻[18]方案與本文方案的，而文獻[18]方案無配對運算，本階段各方案計算量由大到小依次為文獻[17]方案、本文方案和文獻[18]方案;在解密階段，文獻[17]方案對結果驗證成功后，沒有敘述數據用戶具體對搜索結果的解密步驟，所以在解密階段對其計算量和通信量不進行對比,本文方案只有少量的乘法運算和指數運算，文獻[18]方案有多個乘法運算、哈希運算和1個指數運算，所以在本階段本文方案的計算效率較高。

6.3 通信量比較

本節從理論角度分析本文方案與文獻[17，18]方案在通信量開銷方面的優勢。表4中|G1|、|GT|和|Zp|分別表示G1、GT和Zp中元素的長度。

Table 3 Computation comparison表3 計算量比較

Table 4 Storage comparison表4 通信量比較

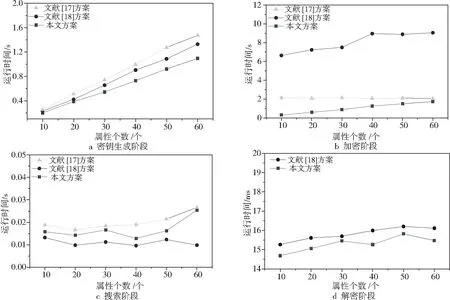
Figure 2 Comparison of algorithm running time圖2 算法運行時間比較

由表4可以看出，在系統化初始階段，文獻[17]方案與本文方案通信量幾乎相同，文獻[18]方案的較高;在密鑰生成階段，隨著屬性個數的增加，每個方案的通信量都有一定的增長，本文方案的效率高于文獻[17，18]方案的;在密文生成階段，各方案通信量由大到小依次為文獻[18]方案、文獻[17]方案和本文方案；在搜索階段，各方案通信量由大到小依次為文獻[17]方案、本文方案和文獻[18]方案;在解密階段，文獻[18]方案中CSP進行部分解密后數據用戶做剩余的解密工作,本文方案中TTP用盲化的私鑰進行部分解密之后用戶只需要簡單計算出密鑰值就能解密得到文件，本文方案的通信量開銷低于文獻[18]方案的。

6.4 數值實驗分析

本文在硬件為3.10GHzCPU，6GBRAM,操作系統為Linux的PC機上利用PBC(Pairing-BasedCryptography)雙線性對包和C語言進行編程模擬實驗。為了便于描述，假設屬性數量|Au|∈[10,60]，圖2a～圖2d給出了文獻[17，18]方案和本文方案在密鑰生成、加密、搜索和解密階段的運行時間對比。由圖2a可知，密鑰生成時間隨著屬性個數的增加，文獻[17，18]方案中指數運算和乘法運算的運行時間都比本文方案的多，所以在密鑰生成階段本文方案效率優于文獻[17，18]方案的；由圖2b可知，在加密階段，隨著屬性個數的增加，通過固定300個關鍵詞對3個方案進行比較，在實際的數值模擬中，文獻[17，18]的效率均低于本文方案的；由圖2c可知，本文方案與文獻[17，18]方案的時間相差不大，由于文獻[17]方案在搜索階段包含指數運算、乘法運算和配對運算，文獻[18]方案與本文方案的計算量相近，故文獻[17]方案的效率最低，搜索階段文獻[18]方案的效率略高于本文方案的；在解密階段,由于文獻[17]方案成功驗證搜索結果后，沒有對搜索結果的解密步驟,所以此階段只比較文獻[18]方案與本文方案，由圖2d可知，本文方案與文獻[18]方案的時間相差較小，文獻[18]方案在解密階段的哈希運算的次數與文件個數相關，計算量消耗比本文方案的高，因此解密階段文獻[18]方案的效率略低于本文方案的。

7 結束語

本文提出了一個面向移動終端的密文可驗證屬性基可搜索加密方案。本文方案為了更好地實現數據用戶的細粒度訪問控制，使用密文策略屬性基加密系統為用戶進行屬性頒發和授權，并且利用SE對存儲在云服務器上的密文數據進行檢索，實現用戶對密文數據的安全共享。為了減少單關鍵詞搜索帶來的大量無關結果，本文方案使用了多關鍵詞可搜索方法。由于云服務器可能會篡改密文數據，本文方案引入了可信第三方對搜索結果進行完整性驗證。為了減輕數據用戶的計算負擔，請可信第三方幫助用戶完成部分解密工作。對于用戶可變的屬性，對相應的屬性進行了更新。最后對本文方案進行了詳細的正確性證明、安全性證明與性能分析，數值實驗分析結果表明：本文方案有較高的效率。