基于分區軟化拉壓桿模型的矩形RC剪力墻水平承載力計算方法
張博鴻,馬高,2
(1.湖南大學土木工程學院,湖南 長沙 410082;2.工程結構損傷診斷湖南省重點實驗室(湖南大學),湖南 長沙 410082)
引言
在實際建筑結構中,剪力墻存在壓、彎和剪共同作用,受力狀態和傳力機理十分復雜。一般認為剪跨比大于2的剪力墻是彎曲控制為主,而對于剪跨比不超過2的剪力墻,在荷載作用下其內部的應力及應變場呈不連續的特征,平截面假定已不再適用,很多學者對這類剪力墻的受力機理、承載能力做了研究和闡述,其中軟化拉壓桿模型是較具有代表性的模型之一。
軟化拉壓桿模型是學者黃世建教授在拉壓桿模型[1]基礎上發展起來的一種新模型。該模型抗剪強度的獲得需編程后反復迭代計算,不易在實際工程中推廣應用。為此,黃世建等[2]于2002年提出了便于設計人員手算的簡化軟化拉壓桿模型。Sanchez-Alejandre等[3]基于該簡化軟化拉-壓桿模型對收集的剪力墻數據庫進行分析,認為軸向荷載和垂直分布筋的配筋率對剪跨比2以下剪力墻的抗剪能力起到了增強作用。Kassem[4]假定剪跨比2以下的剪力墻均為主斜壓桿失效破壞,基于黃世建的簡化軟化拉-壓桿模型和大量試驗數據的擬合,給出了剪跨比2以下剪力墻的承載力計算公式。黃煒等[5]通過擬合參數有限元分析,將軟化拉壓桿模型推廣于復合墻板,提出了相應的斜截面承載力公式。
然而黃世建抗剪承載力模型的假定為主斜壓桿破壞,未考慮拉桿對承載力的影響。就破壞模式而言,這種假定僅適用于剪切破壞,認為主斜壓桿發生破壞時,結構恰好達到承載力峰值,例如劉鳴等[6]、董俊宏等[7]學者將軟化拉壓桿模型運用于節點中,均取得了較好的效果,但根據韓小雷等[8]、Lefas等[9]的剪力墻試驗可知,當在剪跨比小于1時,剪力墻易發生剪切破壞,而剪跨比1~2之間的剪力墻多是彎剪耦合破壞,這導致原軟化拉-壓桿模型的假定在剪力墻中不能廣泛適用。在力學平衡方面,軟化拉-壓桿模型中頂部水平力的抵抗作用并非由斜壓桿單獨完成,而是依靠拉壓桿機構共同完成,僅由斜壓桿承載能力反算剪力墻承載力,忽略了拉桿的限制,會使拉桿控制的剪力墻計算值偏大。此外,通過觀察剪力墻的裂縫特征[10-17],發現其開裂過程存在分區的情況,即受拉暗柱和腹板處于彎剪區或斜壓區,而受壓暗柱處于剪壓區,這說明剪壓區的暗柱也應額外承擔水平荷載。
針對上述問題,文中在原軟化拉壓桿模型的基礎上,提出了考慮拉桿屈服和邊壓桿抗剪作用的分區軟化拉壓桿模型計算方法,并通過剪切破壞和彎剪破壞2類試驗數據與規范公式、相關學者計算模型的對比分析,驗證了該計算方法的有效性。
1 矩形剪力墻數據庫
1.1 數據收集
文中收集了242個矩形RC剪力墻試驗數據[8-14,18-42],多為帶暗柱構造,不包含混凝土強度大于80 MPa、帶交叉鋼筋等改進型鋼筋混凝土剪力墻試驗數據,加載方式大多數為低周往復加載。搜集的數據包含截面尺寸、暗柱長度、剪跨比、軸壓比、混凝土強度、水平分布鋼筋配筋率、豎直分布鋼筋配筋率、暗柱縱筋配筋率等,其中剪跨比2以內的剪力墻190片,剪跨比2以上的剪力墻52片,剪切破壞剪力墻73片,彎剪破壞剪力墻169片。
1.2 數據統計
由圖1可以看出:(1)數據庫中剪力墻剪跨比在0~3之間均有分布,剪跨比小于2的占78.5%,主要為低矮剪力墻,其中剪跨比為0.5~1的剪力墻占比最大;(2)軸壓比以低軸壓比為主,軸壓比0~0.1之間剪力墻占79.5%;(3)混凝土圓柱體抗壓強度主要分布于20~40 MPa;(4)水平分布筋和豎向分布筋配筋率主要集中在0~1%之間;(5)暗柱縱筋配筋率多分布在0~6%之間。

圖1 剪力墻數據庫各參數頻率分布Fig.1 Frequency distribution of the parameters of shear wall data base
2 軟化拉壓桿模型
剪力墻的軟化拉壓桿模型如圖2所示,Vd、Vh、Vv代表各機構所承擔的抗剪能力,結構總抗剪能力為各機構抗剪能力之和。

圖2 剪力墻的軟化拉壓桿模型Fig.2 Softened strut-and-tie model of shear wall
文中先簡要介紹軟化拉壓桿模型的簡化計算方法,公式中各系數的詳細推導過程參見文獻[2]。模型總抗剪能力V1的計算公式為:

式中:K為拉壓桿系數;ζ為開裂混凝土軟化系數;f'c為混凝土圓柱體抗壓強度;Astr為斜壓桿有效面積;θ為斜壓桿與水平方向夾角。各項具體可寫為:

式中:as為斜壓桿高度;bs為斜壓桿寬度,取墻厚;H為剪力墻墻片高度;h為加載梁高;l為剪力墻計算長度。各項具體可寫為:


式中:b為剪力墻厚;N為墻上承擔的豎向荷載;Ag為剪力墻截面面積;L為剪力墻長度;la為暗柱長度,無暗柱時取0.2L。
式(1)中拉壓桿系數K可以寫為:

式中:Kh、Kv為水平拉桿、豎向拉桿修正系數,其作用為修正拉桿發揮程度,形式如下:

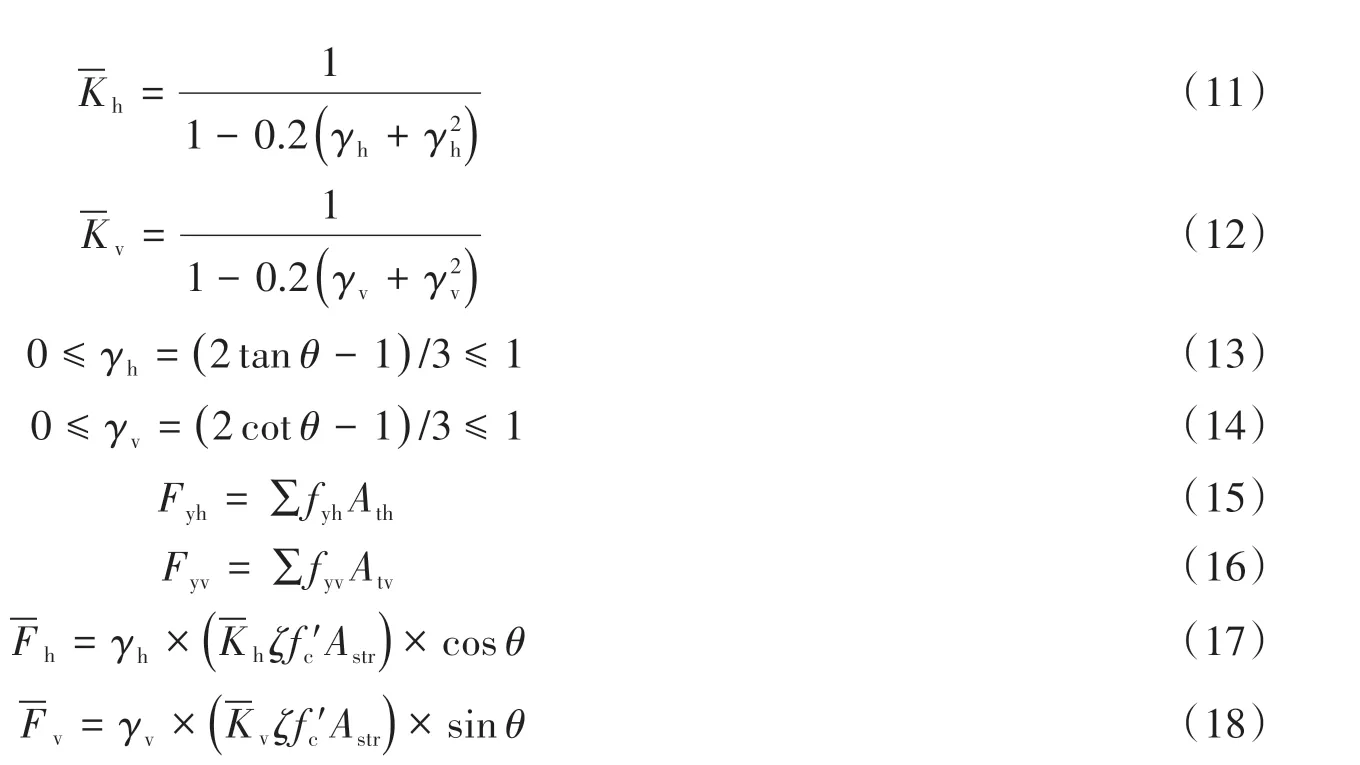
式中:γh為水平拉桿與節點水平剪力的比值;γv為豎向拉桿與節點豎向剪力的比值;fyh、fyv為水平鋼筋、豎向鋼筋的屈服強度;Ath為水平鋼筋截面面積,取墻高0.25~0.75H范圍內全部水平分布鋼筋面積以及該范圍外水平分布鋼筋面積的一半[1],以考慮水平筋的實際貢獻;Atv為全部豎向分布筋截面面積。
3 分區軟化拉壓桿模型
3.1 剪力墻受力機理分析
基于剪力墻彎剪破壞的試驗現象[10-11](圖3(a)所示),依據其裂縫的發展規律及受力狀態的特點,可分為彎剪、剪壓2個區域,即:受拉暗柱及腹板處于彎剪區,其裂縫屬于彎剪裂縫,數量較多,越接近剪壓區,裂縫受壓力影響越大,裂縫越偏于陡峭,一般發展至受壓暗柱內側邊緣;受壓暗柱則處于剪壓區,其在承載力峰值時,承受較大壓力,裂縫數量不多。
而對于發生脆性剪切破壞的剪力墻[12-14](圖3(b)所示),可分為斜壓、剪壓2個區域,即:受拉暗柱及腹板處于斜壓區,其裂縫屬于典型通長斜裂縫,數量較多,其通長主斜裂縫近似對角發展,受壓暗柱依然處于剪壓區,其在承載力峰值時,會出現若干斜裂縫,此斜裂縫較主通長裂縫更陡峭。以上特征表明剪力墻存在2個分區且工作機理存在差異。
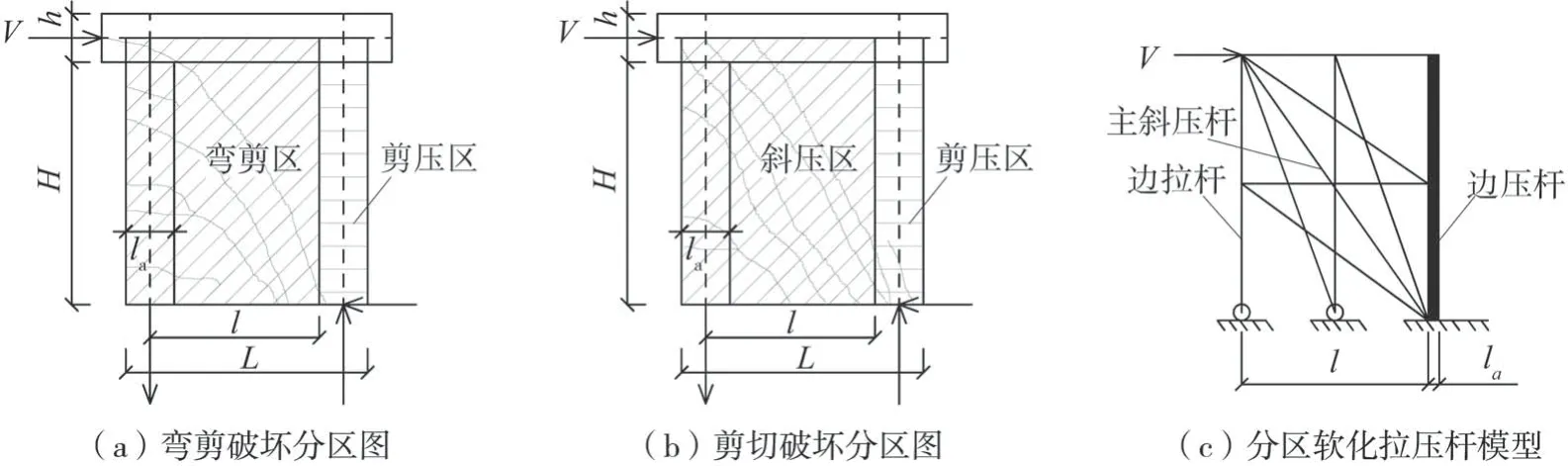
圖3 剪力墻受力分區圖及分區模型Fig.3 Force partition diagram of shear wall and partition model
對于受拉暗柱和腹板而言,受拉暗柱區域出現較為水平的裂縫,表明縱筋受拉力;腹板出現斜裂縫,表明腹板受拉、壓共同作用。當斜壓桿破壞而拉桿未屈服時,結構會呈現脆性剪切破壞,形成斜壓區;而當拉桿先屈服時,桁架承載力將由拉桿控制,產生彎曲裂縫,后因結構變形導致斜壓桿強度軟化而最終發生主斜壓桿破壞或暗柱角部破壞時,結構會呈現彎剪破壞,形成彎剪區。對于受剪切和壓力共同作用的受壓暗柱(邊壓桿),其受力機理與傳統抗剪原理相似,為水平筋屈服和暗柱混凝土在剪力和壓力的復合作用下,主拉應力超過其抗拉強度而破壞或在高軸力下被壓碎。2個分區貢獻的疊加即為剪力墻總水平承載力。最終的剪力墻分區軟化模型如圖3(c)所示,該模型中當邊拉桿屈服先于主斜壓桿破壞時,對應圖3(a)的彎剪破壞,當主斜壓桿破壞先于邊拉桿屈服時,對應圖3(b)的剪切破壞。
3.2 分區軟化拉壓桿模型計算概念
受拉暗柱和腹板抗水平力貢獻符合軟化桁架模型,但原軟化模型未考慮拉桿對桁架水平承載力的限制作用,故需要補充軟化桁架在拉桿控制下的水平承載力計算概念,具體表述為:總剪力按原軟化拉壓桿模型給出的分配比例式(19)~式(21)分配至各機構(如圖2所示),當水平和豎向機構均不屈服時,分配比例見式(20)~式(21),若某一機構先屈服,剩余機構分配比例按式(19)計算[2],水平和豎向機構均屈服后,水平力僅由斜向機構承擔。當邊拉桿屈服時,若豎向機構的中拉桿未屈服,則剪力墻承載力可繼續增長至中拉桿屈服,但在此過程中需考慮邊壓桿受壓抗力的限制,若在中拉桿屈服前,邊壓桿角部所受豎向力超過其受壓抗力,則邊壓桿破壞,中拉桿無法完全屈服。
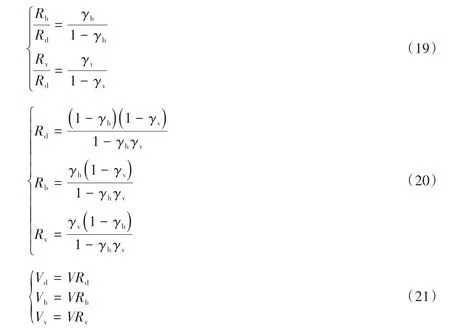
基于上述拉桿控制下的剪力墻承載能力計算概念,再結合原軟化拉壓桿的斜壓桿控制計算概念,兩者計算結果取小值,便可求得剪力墻受拉暗柱和腹板區域的實際抗剪承載力貢獻。除此之外,作為邊壓桿的受壓暗柱區域會為結構提供額外的水平承載力,其貢獻可按剪壓概念求解。兩個分區貢獻的疊加即為剪力墻總水平承載力。
3.3 分區模型組成部分定義
如圖3可知,考慮各分區上方所受實際豎向荷載的影響,將式(5)和式(7)修改為式(22)和式(23),其中la為暗柱長度,無暗柱剪力墻的暗柱長取0.2L,L為剪力墻長度。
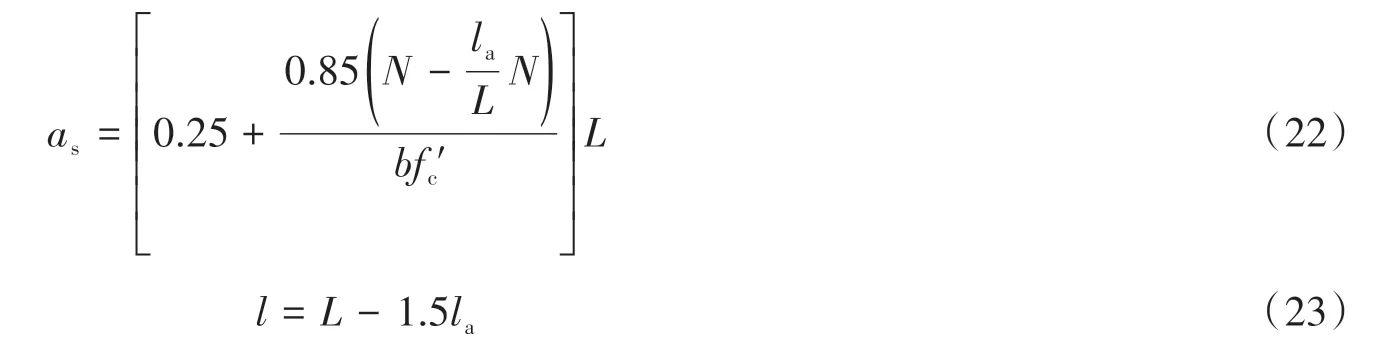
計算剪跨比取剪力墻高和加載梁高的一半與計算模型長度的比值:

邊拉桿抗力取暗柱內的縱筋屈服力和暗柱上方分配的豎向荷載之和,其中Aaz為暗柱縱筋面積:

中拉桿抗力取全部豎向分布筋屈服力和腹板上方分配的豎向荷載之和,Atv為全部豎向分布筋面積:

水平機構中水平拉桿抗力由水平分布筋屈服力構成:

壓桿角部受壓抗力按下式計算,Aa為暗柱面積:

3.4 邊拉桿貢獻計算
由圖2桁架模型可知,雖然水平或中拉桿屈服會導致其對應的機構屈服,從而使機構間分配比例發生變化,但機構各自頂部所承擔水平力與邊拉桿最大受力部分的比值總是等于計算剪跨比,因此無論機構間內力如何分配,各機構邊拉桿受力總和與承擔水平力總和的比值也總等于計算剪跨比。故邊拉桿的抵抗水平力貢獻不受機構間分配比例的影響,其值為:

3.5 中拉桿額外貢獻計算
在計算邊拉桿貢獻時,其中豎向機構所分配的剪力不足以讓中拉桿屈服的情況下,結構可通過繼續變形使中拉桿繼續受力,此時新增長的中拉桿受力,文中定義為中拉桿額外抗力,記為Fzle。
當各機構均不屈服時,豎向機構的邊拉桿受力為FblRv,其中豎向機構的邊拉桿與中拉桿受力相等,所以當FblRv≥Fzl時,中拉桿屈服,故不能提供額外抗力;仍在FblRv≥Fzl條件下,當由于水平拉桿配置不足,導致水平機構先屈服時,會使豎向機構承擔到比原來(FblRv)更大的力,此時中拉桿也會屈服無額外貢獻。故有式(30),其中Fzle為中拉桿額外抗力:

當FblRv<Fzl時,中拉桿額外貢獻將受水平機構的影響,當水平機構不屈服時,可先求出水平機構的邊拉桿受力FblRh,然后剩余邊拉桿抗力中豎向機構的邊拉桿受力可按(Fbl-FblRh)γv計算,若(Fbl-FblRh)γv>Fzl,則說明中拉桿屈服,此時中拉桿無額外抗力,故中拉桿額外抗力有如式(31):
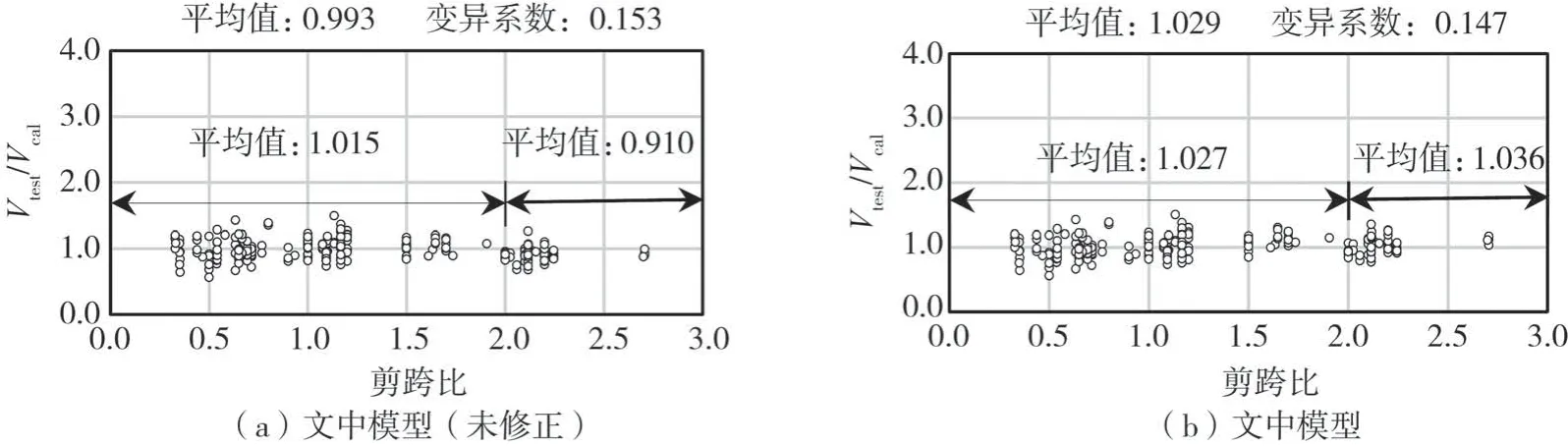
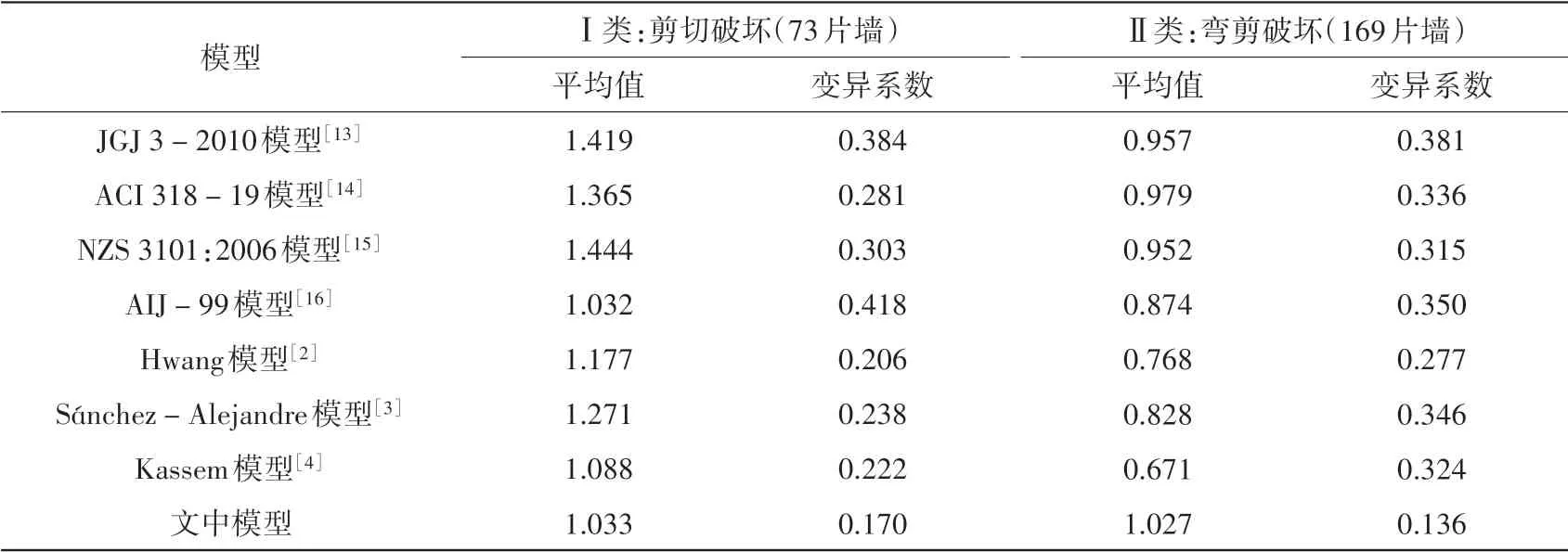
FblRv 在FblRv<Fzl的情況下,若水平機構屈服,則水平機構的受力將由水平拉桿抗力控制,根據水平機構桁架模型中水平拉桿與邊拉桿受力關系可知,此時水平機構邊拉桿受力為Fslλ′,同上可求得此時中拉桿額外抗力為: 除此之外,還需考慮邊壓桿角部受壓抗力對中拉桿額外抗力發揮程度的限制,即壓桿角部受壓抗力要大于等于壓桿本身所受豎向荷載、邊拉桿貢獻計算時通過機構傳遞來的豎向壓力、中拉桿額外貢獻計算時傳遞過來的豎向壓力之和,故壓桿角部受壓抗力限制下中拉桿額外可發揮抗力為: 最后Fzle1、Fzle2、Fzle3三者取小值,并根據幾何關系可由中拉桿額外抗力求得中拉桿額外抵抗水平力貢獻。 根據上述推導可知,腹板縱筋可與混凝土斜壓桿組成桁架機構抵抗水平力,但其受力較為復雜,腹板縱筋貢獻受到模型的分配比例、暗柱縱筋抗力、水平分布筋抗力、豎向分布筋抗力、軸力、剪跨比及受壓暗柱角部受壓抗力的影響。其中,隨著剪跨比的降低,豎向機構分配比例逐漸增大,彎剪區受剪切影響逐漸增加,其抵抗水平力的貢獻會受到抑制。 邊壓桿由受壓暗柱構成,其主要受剪力和壓力的復合作用,可按傳統剪壓原理去考慮,即邊壓桿的抗剪貢獻可分為混凝土貢獻Vcb和鋼筋貢獻Vsb。 受壓暗柱混凝土貢獻Vcb,根據材料力學理論可按式(36)求得[43], 式中:b為墻厚。邊壓桿鋼筋貢獻Vsb仍采用45o桁架模型來計算,計算長度取暗柱長度可得式(37), 式中,ρh為水平分布筋配筋率。則邊壓桿抗剪承載力貢獻可表示為: 根據上文可知拉桿控制的剪力墻受拉暗柱和腹板區域水平承載力公式可表示為: 結合原軟化拉壓桿方法,剪力墻受拉暗柱和腹板區域最終水平承載力貢獻可表示為: 疊加受壓暗柱區域邊壓桿抗剪貢獻的剪力墻水平承載力公式可表示為: 為測試公式的適用范圍,將全部剪力墻(共242片)代入公式進行驗證,效果如圖4(a)所示。可觀察到試驗值比計算值(Vtest/Vcal)的平均值、變異系數和平均誤差均較好,但剪跨比大于2的數據平均值偏低,這說明對于中剪跨比的剪力墻,文中計算方法計算值偏大,這是由于暗柱混凝土貢獻均按最大值疊加計算造成的。根據試驗現象[10-14],在承載力峰值時中剪跨比剪力墻較低剪跨比剪力墻受壓暗柱區域完整度更高,說明隨著剪跨比的增大,受壓暗柱抗剪貢獻的發揮程度在降低。為考慮剪力墻剪跨比的影響,同時保持公式中系數的簡潔,文中以混凝土貢獻比上計算剪跨比進行修正,并考慮到修正后的混凝土貢獻不得大于理論上混凝土所能提供的最大抗剪承載力值,故有式(42)。修正后的公式預測效果如圖4(b)所示,可觀察到預測值隨剪跨比的變化平穩。 圖4 文中模型水平承載力預測結果Fig.4 Horizontal bearing capacity prediction results based on the current model 文中將低剪跨比剪力墻數據庫分為剪切破壞(I類,73片)和彎剪破壞(Ⅱ類,169片)2類,并選取了7個具有代表性的規范及相關學者提出的剪力墻抗剪承載力公式進行分類對比分析。表達式中的符號已與前文進行了統一,前文未提及的變量均在下方進行了注釋。將2類數據庫中各試件參數分別代入文中公式與文獻公式,計算試驗值比計算值的平均值與變異系數,如圖5和表1所示。對于規范公式,亦采用材料的實測強度值代入進行計算。圖5中的剪跨比按λ=(H+0.5h)/L計算。文獻公式簡要介紹如下: 圖5 規范及文獻水平承載力預測結果Fig.5 Horizontal bearing capacity prediction results based on codes and literature (1)中國規范JGJ 3-2010[44] 式中:λ0取(H+0.5h)/h0,其中H為墻高,h0取L-0.5la,L為墻長,h為加載梁高,λ0小于1.5時,取1.5,大于2.2時,取2.2;N為軸力,大于0.2fctL時,取0.2fctL,t為墻厚;sv為水平分布鋼筋的豎向間距;βc為混凝土強度影響系數,當fcu不超過C50時,βc取1.0,當fcu大于C80時,βc取0.8,其間按線性內插法確定;Ash為配置在同一截面內的水平分布筋的全部截面面積。 (2)美國規范ACI 318-19[45] 式中:αc為混凝土強度對墻抗剪強度的貢獻系數,當λ小于1.5時,取0.249,當λ大于2.0時,取0.166,其間按線性內插法確定;ρh為全部水平鋼筋截面面積與水平鋼筋垂直剪力墻面的面積之比;fyh為水平分布筋屈服強度。 (3)新西蘭規范NZS 3101:2006[46] 式中:vc1、vc2為混凝土抗剪強度,vc1取0.27f'0.5c+N/(4Ag),vc2取0.05f'0.5c+L(0.1f'0.5c+0.2N/Ag)/(M/V-L/2),當M/VL/2≤0時,只取vc1;d為有效墻長,取0.8L。 (4)日本規范AIJ-99[47] 式中:v為混凝土有效抗壓強度系數,取0.7-f'c/200;tanθ0取[(H0/l)2+1]0.5-H0/l;β為桁架機制中混凝土斜壓桿的壓應力與混凝土有效強度之比,取(1+cot2ξ)ρhfyh/(vf'c);H0為加載點至墻底垂直距離;l為計算長度取L-la;fyh為水平分布筋屈服強度,超過400 MPa時取400 MPa,當ρhfyh大于vf'c/2時,取vf'c/2;ξ為桁架機構中混凝土斜壓桿傾角,對于墻cotξ取1。 (5)Hwang模型[2] 模型公式和含義參見前文。 (6)Sánchez-Alejandre模型[3] 式中:γ取0.42-0.08λ;ηv取0.75+0.05ρvfyv;ηh取1-0.16ρhfyh≥0.2;ρv為豎向分布鋼筋截面面積與豎向鋼筋垂直剪力墻面的面積之比;ρh為全部水平鋼筋截面面積與水平鋼筋垂直剪力墻面的面積之比;fyh為水平分布筋屈服強度;fyv為豎向分布筋屈服強度。 (7)Kassem模型[4] 式中:Ψ取0.95-f'c/250;ks取as/dw;dw取do-as/3;α取tan-1(Hw/dw);ωh取ρhfyh/f'c;ωv取ρvfyv/f'c;d0為縱向受拉鋼筋合力到受壓邊緣距離,取L-0.5la;Hw為加載點到底梁距離;ρv此處為豎向分布鋼筋截面面積與剪力墻厚度和dw乘積的比值。 由圖5和表1可知中國規范JGJ 3-2010模型在計算I類數據庫時的Vtest/Vcal整體偏高(1.419),且隨著剪跨比的降低平均值明顯增大,說明其設計公式較為保守,特別是在低剪跨比范圍,此外規范計算結果的變異系數也較大(0.384);美國規范ACI 318-19在計算I類數據庫時Vtest/Vcal的變異系數(0.281)比中國規范稍好,但也偏于保守(平均值為1.365),同時也存在隨剪跨比的降低計算值越來越保守的問題;新西蘭規范在計算I類數據庫時的統計參數與中國美國規范類似;日本規范的計算原理是基于桁架模型和拱模型,其在計算I類數據庫時Vtest/Vcal的平均值較為準確(1.032),但變異系數較大(0.418);對于Sánchez-Alejandre模型,在計算I類數據庫時,模型的預測值較為保守,但變異系數較小(0.238);Kassem模型在計算I類數據庫時,結果整體上較為準確(Vtest/Vcal平均值為1.088),變異系數也較小(0.222);Hwang模型在計算I類數據庫時,計算結果的變異系數(0.206)較好但平均值較為保守(1.177),在計算Ⅱ類數據庫時,由于未考慮拉桿控制導致計算值整體偏不安全(平均值0.768),文中模型在計算I類和Ⅱ類數據庫時,計算結果的變異系數均最小(0.170和0.136)、平均值均較為準確(1.033和1.027),又由圖4(b)可知模型預測結果隨剪跨比的變化穩定,說明該計算模型能合理反映剪力墻受力機理隨剪跨比的變化情況。 表1 水平承載力Vtest/Vcal的統計參數Table 1 Statistical parameters of horizontal bearing capacity Vtest/Vcal 對比上述規范與文獻模型的計算結果可知,對于Ⅰ類數據庫,各國規范計算公式(除日本規范),整體較為保守,變異系數均較大,而學者提出的抗剪公式相比規范在在平均值和變異系數上均有改善,但目前的抗剪公式均無法在Ⅱ類數據庫中適用,這是因為彎剪破壞的剪力墻既受到彎的影響又受到剪的影響,需要考慮彎剪耦合。對于文中模型,基于Hwang的模型考慮了彎剪分區后,在Ⅰ類數據庫和Ⅱ類數據庫中Vtest/Vcal的平均值和變異系數相對于原模型得到了明顯改善,且該模型基于力學推導,對于剪切和彎剪均適用。因此文中提出的改進軟化拉壓桿方法較為合理,可為剪力墻剪切和彎剪模型的相關研究提供參考。此外,文中模型表達式較簡潔、物理意義明確,可為實際工程提供指導。除根據公式可對剪力墻配筋等相關參數進行設計外,還可從拉桿與壓桿的受力關系出發,設計拉桿先于壓桿屈服,使剪力墻在地震下的破壞形式為延性破壞,避免非延性破壞。 (1)剪力墻抵抗水平力的工作機制存在分區行為,受拉暗柱和腹板處于彎剪區或斜壓區,其彎剪機制符合軟化桁架模型;受壓暗柱處于剪壓區,其抗剪機制符合混凝土構件剪壓原理。其中剪切破壞可通過模型的斜壓區疊加剪壓區表達,彎剪破壞可通過模型的彎剪區疊加剪壓區表達。 (2)文中所提出的考慮拉桿屈服及邊壓桿抗剪的分區軟化拉壓桿模型,在剪切破壞和彎剪破壞兩類數據中的變異系數對比規范和文獻其它方法均有顯著降低,平均值也更準確,且文中基于力學推導的分區模型在各剪跨比區間計算結果的平均值均較為穩定,說明文中模型適用范圍較廣,能合理反映剪力墻的工作機理。此外,該方法不需要迭代,計算過程簡便,適用于實際工程應用。 (3)建議在剪力墻設計時,通過增大混凝土強度等方式,使文中所提剪切破壞公式中的V1大于彎剪破壞公式V2,即讓剪力墻中拉桿屈服先于主斜壓桿破壞,從而使低矮剪力墻避免純剪切破壞。同時可通過調節彎剪公式V2中水平和豎向分布筋的配筋量進行合理配筋,避免配筋過少時剪力墻承載力過低發生剪切破壞或配筋過多時出現無效配筋而造成浪費。 (4)文中模型破壞機理按裂縫劃分,模型適用于剪跨比3以下的以斜向裂縫為主的剪切破壞矩形RC剪力墻和水平裂縫與斜向裂縫并存的彎剪破壞矩形RC剪力墻,但對于剪跨比大于3剪力墻的適用性,需要進一步研究。



3.6 邊壓桿貢獻計算



3.7 方法驗證及分析




4 模型比較與分析

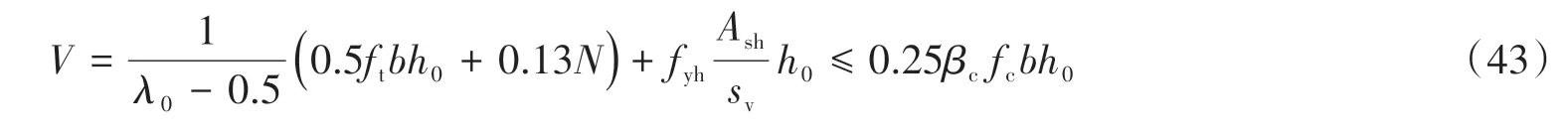
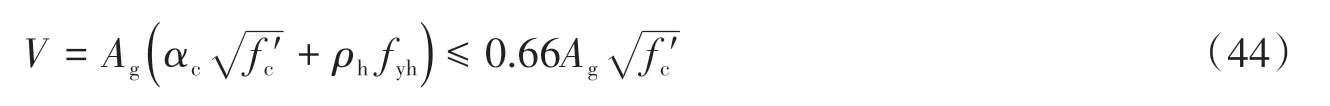
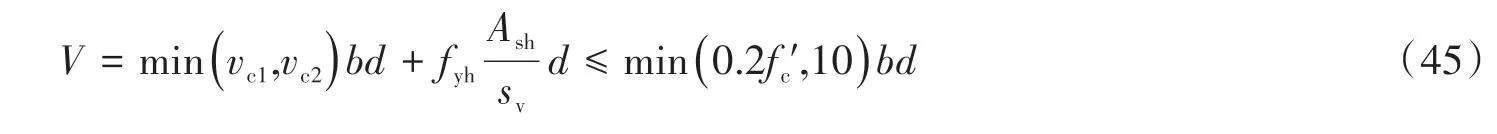
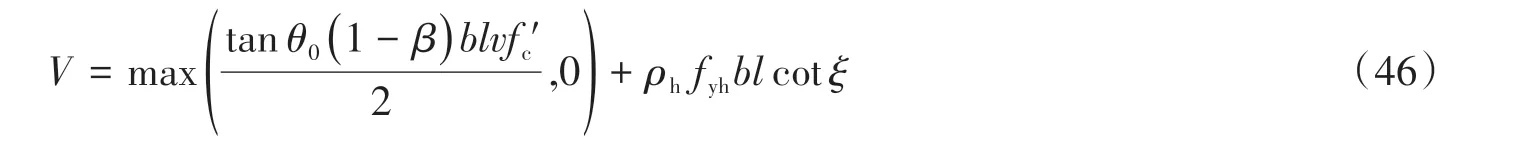
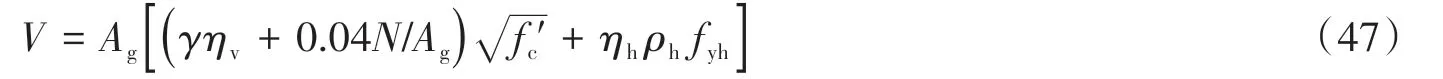
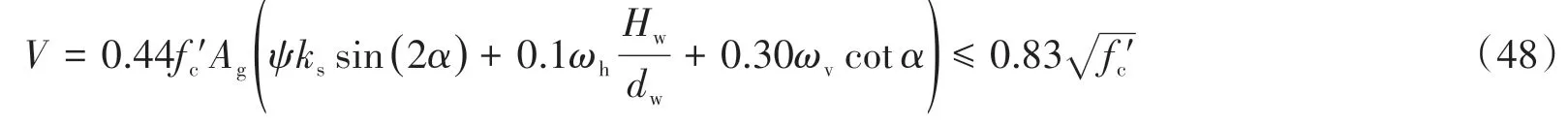
5 結論

