基坑抗隆起穩定性研究新進展
張京伍, 張海洋, 李明東, 鄒白濤, 李衍翔
(東華理工大學土木與建筑工程學院, 南昌 330013)
21世紀是地下空間開發利用的時代。隨著中國城市化進程的加快,城市用地越發緊張,結合城市建設和改造的地下空間工程開發規模越來越大[1-4],這些工程無一例外地都要涉及基坑開挖問題,如何保證基坑穩定性是基坑工程的重要研究方向[5-8],坑底隆起是影響基坑安全的關鍵因素之一[9]。坑底隆起一方面造成基坑坍塌,影響在建基坑安全;另一方面導致鄰近建(構)筑物的不均勻沉降,甚至垮塌。這些事故的產生與坑底抗隆起分析理論的不完善有著密切關系。
坑底隆起破壞機制主要分為地基承載力模式[10]及圓弧滑動破壞模式[11]。其中地基承載力法以驗算支護結構底面土體地基承載力作為抗隆起穩定性的依據;圓弧滑動法結合邊坡穩定性分析理論,通過假定潛在滑裂面,以抗滑力矩與滑動力矩的比值為安全系數判斷坑底穩定性。基坑抗隆起穩定性分析方法主要有極限平衡法、極限分析法以及數值分析法。極限平衡法需要事先假定一個破壞面,計算原理簡明,往往在實際工程中得到應用[12];極限分析法以塑性力學的理論為依據,根據功能相等原理,得到基坑抗隆起穩定安全系數的上下限,使其結果更為可靠[13];數值分析法通常是運用數值模擬軟件,在強度折減法的基礎上計算出坑底抗隆起安全系數[14]。
現針對近10年基坑抗隆起穩定性研究進展,探究基坑寬度、土體各向異性及支擋結構嵌固深度對基坑抗隆起穩定性的影響規律。對目前中外基坑工程設計運用到的兩種抗隆起極限平衡分析方法做深入探討,總結改進后計算方法的適用范圍;進一步指出定量分析方法并不能有效計算坑底隆起的失效概率,運用可靠度分析方法能有效補充坑底抗隆起穩定性分析理論。對圓形基坑坑底隆起的破壞機制及安全系數的計算方法進行闡述,指出圓形基坑坑底穩定性驗算方法存在的問題;同時對坑中坑式基坑破壞機制的臨界值劃分、坑底穩定性的影響因素進行總結。
1 基坑抗隆起穩定性影響規律
1.1 基坑寬度影響
狹窄基坑坑底具有很好的穩定性[15-16]。對于深厚淤泥區的基坑抗隆起穩定性分析,使用有限元強度折減法計算得到的基坑抗隆起安全系數隨基坑寬度增大而減小,基坑寬度由25 m減小至14 m時,基坑抗隆起安全系數增加了17%左右,當基坑寬度大于25 m時,安全系數變化不明顯[14];俞建霖等[17]通過實際工程案例對比在不同土層性質下基坑寬度對基坑坑底抗隆起穩定性的影響,指出當圍護結構大于基坑寬度時,基坑寬度由25 m減小至14 m,淤泥質土地基中基坑抗隆起安全系數增加了41.0%,粉土地基中增加了43.4%。王洪新等[12]更加詳細地劃分了基坑寬度范圍對基坑抗隆起安全系數的影響,當基坑寬度小于5 m時,減小基坑寬度,抗隆起安全系數急劇變大;5 m增至15 m時,緩慢變化;大于15 m時,安全系數變化不大。張飛等[13]在不同基坑開挖深度下,討論基坑寬度對基坑抗隆起安全系數的影響,當基坑寬度在0.5倍開挖深度內增加基坑寬度,基坑抗隆起安全系數會急劇下降;當基坑寬度大于開挖深度時,基坑抗隆起安全系數變化緩慢。
1.2 土體強度各向異性影響
眾多學者已認識到土體強度各向異性對基坑穩定性存在影響,特別是在軟土層厚度及基坑寬度較大的基坑設計中,不考慮土體強度的各向異性將無法保證基坑設計結果的準確性[18]。孔德森等[19]基于Casagrande各向異性強度理論,采用考慮圓弧滑動破壞模式的極限平衡法,推導出考慮土體強度各向異性參數的坑底抗隆起穩定計算公式;周建等[20]給出軟土基坑抗隆起穩定不排水抗剪強度極限平衡解。采用極限分析上限法研究基坑抗隆起穩定性時,發現忽略土體強度各向異性將會高估抗隆起安全系數[21]。
研究表明各向異性比的提高降低了安全系數[22-23]。針對杭州地區軟黏土,已有學者通過開展復雜應力路徑下不排水抗剪強度試驗,提出能夠考慮土體各向異性不排水抗剪強度的理論公式,發現不考慮土體強度各向異性將導致基坑抗隆起穩定性計算結果偏于不安全[24]。Liao等[25]、Su[26-27]通過對比有無灌注樁加固黏土的強度各向異性特性,認為灌注樁加固后黏土的各向異性強度特性更為顯著,忽略加固后土體強度各向異性的影響會高估坑底隆起的安全系數,同時基于提出的各向異性強度準則,確定坑底灌注樁加固的抗隆起安全系數。
1.3 圍護結構嵌入深度影響
Tang等[28]基于極限分析上限理論研究均質黏土基坑的圍護墻嵌入深度對基坑抗隆起穩定性影響,得出抗隆起安全系數隨著連續墻嵌入段的加深而逐漸增大的結論。周建等[20]基于圓弧滑動法分析地下連續墻不同嵌入深度下的軟土基坑抗隆起穩定性,認為隨著擋墻入土深度的增加,安全系數增加的幅值不斷減小,當插入比大于1時,無需過多增加擋墻入土深度即可保證坑底穩定。針對處于海積淤泥土的圍護樁支護基坑中,也得到了相同的結論[29]。
研究表明圍護結構端部嵌固層土層特性對基坑抗隆起穩定性存在影響。當樁端處于坑底軟弱土層且土層分布較厚時,增加樁體的嵌入深度對抗隆起安全系數的提高影響不大[30],相較于樁墻,連續墻入土深度的增加對基坑抗隆起安全系數的影響更加顯著[31]。當擋墻端部位于均質軟黏土且未進入較堅硬土層時,擋墻嵌入深度逐漸增加反而導致抗隆起安全系數減小[32],表明擋墻端部位于較堅硬土層才能保證基坑的穩定性。
2 基坑抗隆起計算方法改進及可靠度分析
2.1 地基承載力模式
基坑抗隆起驗算采用的地基承載力模式是以驗算圍護結構底面的地基承載力作為抗隆起穩定的依據。坑底是否穩定與土體黏聚力、土體重度及地面超載共同作用有關,實際計算時,將基坑基準面以上的坑內、坑外土體等效為超載,而后采用地基承載力模式計算坑底的抗隆起安全系數。計算原理如圖1所示。
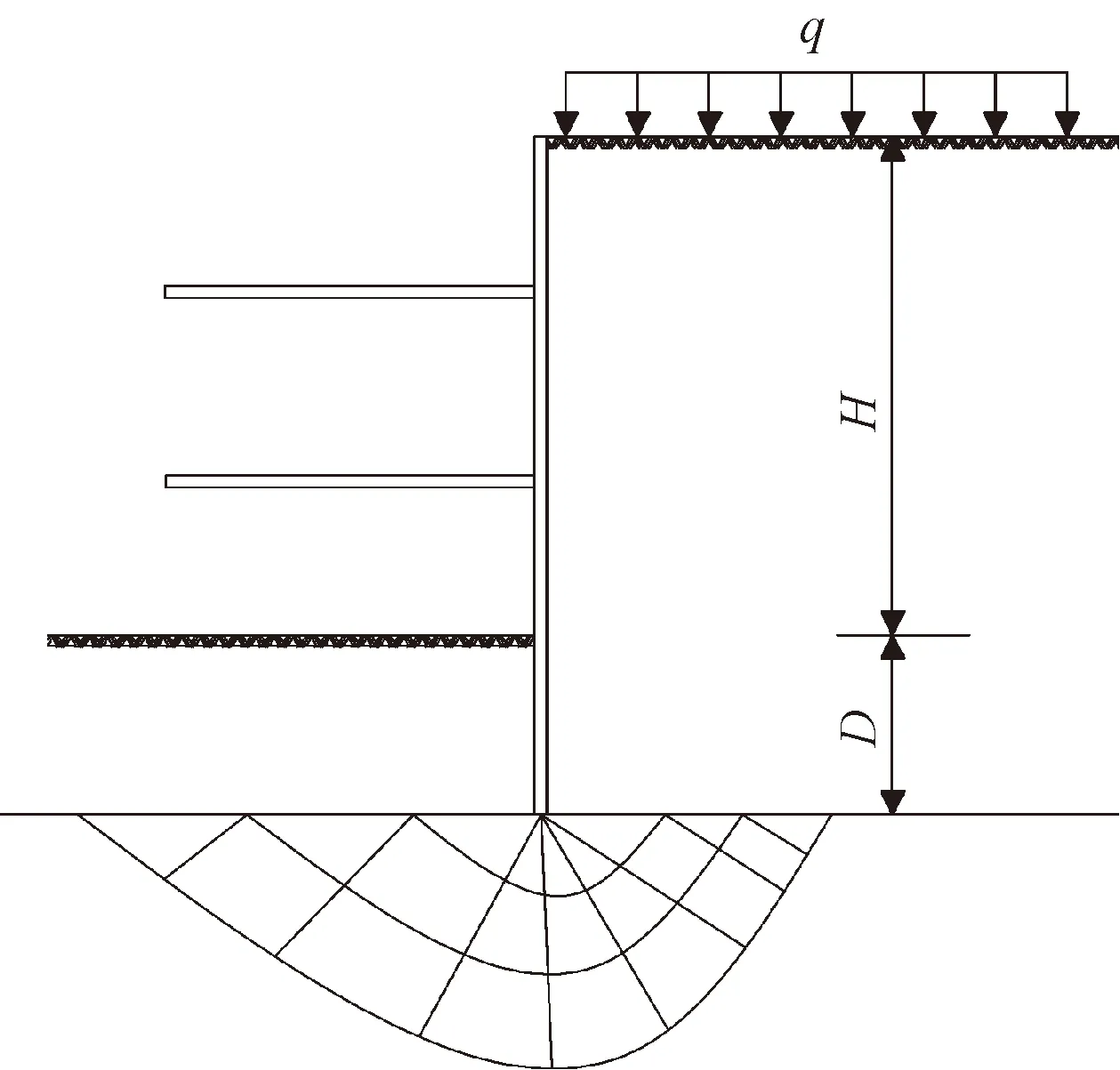
q為坑外地面荷載,kPa;H為基坑開挖深度,m;D為圍護墻體在基坑開挖面以下的入土深度,m
已有的地基承載力公式忽略了基坑開挖寬度、圍護結構嵌深范圍內土體抗剪強度及坑外下沉土體與穩定土體間剪力等有利作用下的影響[34],導致計算出來的抗隆起安全系數偏差較大。宋二祥等[35]對傳統的地基承載力模式計算方法進行了改進,考慮坑外下沉土體與穩定土體間剪力影響,計算結果經有限元極限分析方法的檢驗,表明了該改進公式的合理性。陽吉寶[36]考慮基坑墻底以上內外側土體間抗滑作用影響,以基坑的寬深比值3為界限,提出一組改進的基坑坑底抗隆起安全系數計算公式,如式(1)、式(2)所示。
(1) 基坑寬度L>3H。
(1)
(2) 基坑寬度L<3H。
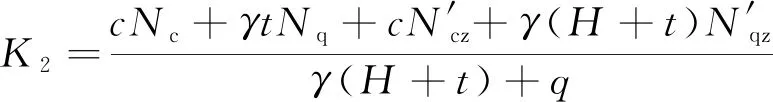
(2)
式中:c為土體的黏聚力,kPa;t為基礎擋墻入土深度,m;Nc、Nq為地基承載力系數;γ為土的重度,kN/m3;N′c、N′q為基礎寬度L>3H時的過渡公式;N′cz、N′qz為基礎寬度L<3H時的過渡公式。
Zhou等[37]考慮圍護墻與土體間摩擦力,改進了坑底隆起地基承載力模式計算公式,如式(3)所示,計算結果更接近實際監測結果。
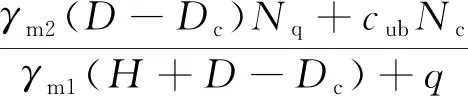
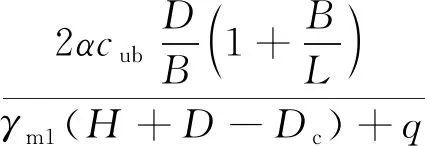
(3)
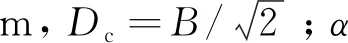
朱磊等[38]采用單側滑動假設且考慮滑動土體豎向抗剪,推導出土釘支護工況下基坑抗隆起安全系數計算方法,如式(4)所示,計算結果比Terzaghi承載力系數法更準確。
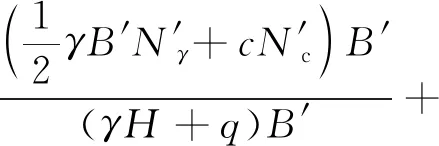
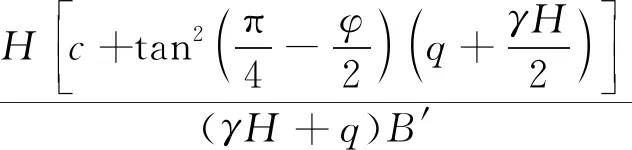
(4)
式(4)中:γ為坑外地表至坑底各土層天然重度的平均加權值,kN/m3;φ為土體的內摩擦角,(°);B′為假想實體基坑寬度,m;N′c、N′γ為過渡公式。
王成華等[39]針對基坑隆起破壞為單面滑動失穩的假設,定義發生最可能隆起失穩破壞的坑位基坑寬度為臨界寬度,如式(5)所示,根據臨界寬度再計算出最小抗隆起安全系數,進一步驗證了改進方法是可靠的。
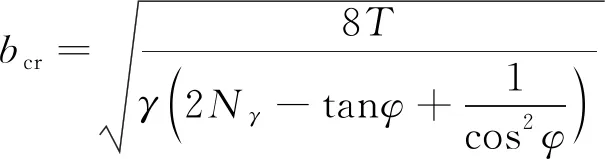
(5)
式(5)中:T為滑動體豎向抗剪切力。
進一步對比分析了4種不同坑底隆起地基承載力模式改進計算方法的破壞機制、適用性、相互聯系及存在的問題,如表1所示。
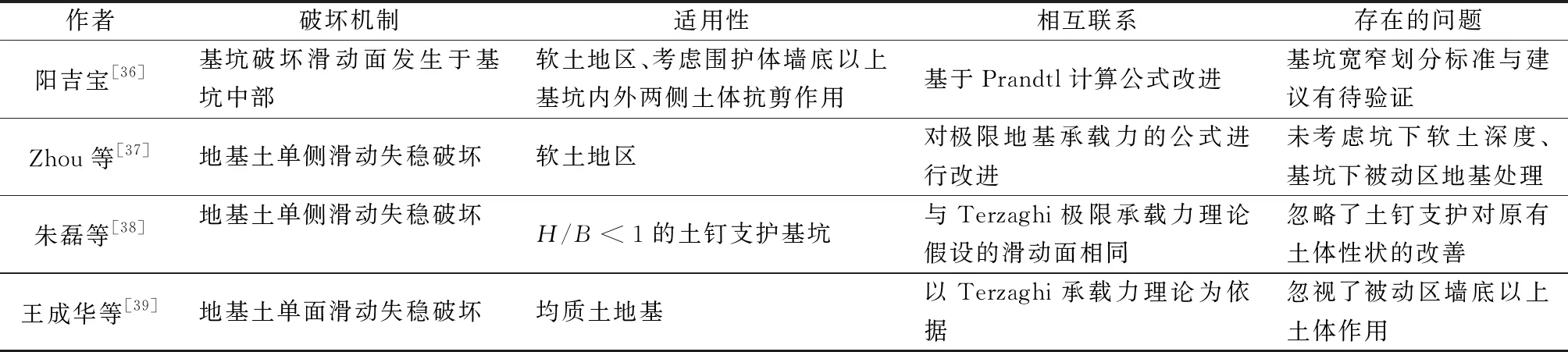
表1 地基承載力模式計算方法改進匯總比較
2.2 圓弧滑動模式
圓弧滑動法計算原理如圖2所示,圓弧滑動法的破壞模式是假定滑裂面穿過連續墻底部、以最下道支撐和連續墻的交點為軸心的圓弧,其計算模式以繞最下道支撐的抗滑力矩與滑動力矩的比值為抗隆起安全系數。
圓弧滑動模式假定了滑裂面為圓形,且剛好經過擋土構件下端。但這一假設并未得到驗證,與實際情況不符的假設在一定程度上必然會導致計算得到的安全系數存在偏差。為提高計算結果的準確性,王洪新等[41]考慮修正被動區加固提供的附加抗滑力矩來改進滑動圓弧法的計算公式,如式(6)所示。
(6)
式(6)中:c為加固區土體天然黏聚力;B為加固寬度;L為加固體凈間距;d為加固體深度;Δc、D′為過渡公式;α為圖2中of與水平面夾角。
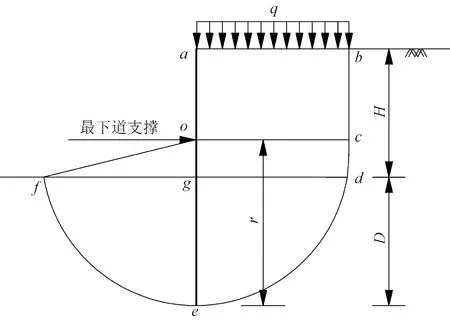
r為滑動破壞半徑
鄭剛等[42]基于圓弧滑動法對分層地基的計算按弧長及滑動面法向應力進行了改進,計算原理如圖3所示,并提出如式(7)、式(8)所示的加權抗剪強度指標修正值表達式。
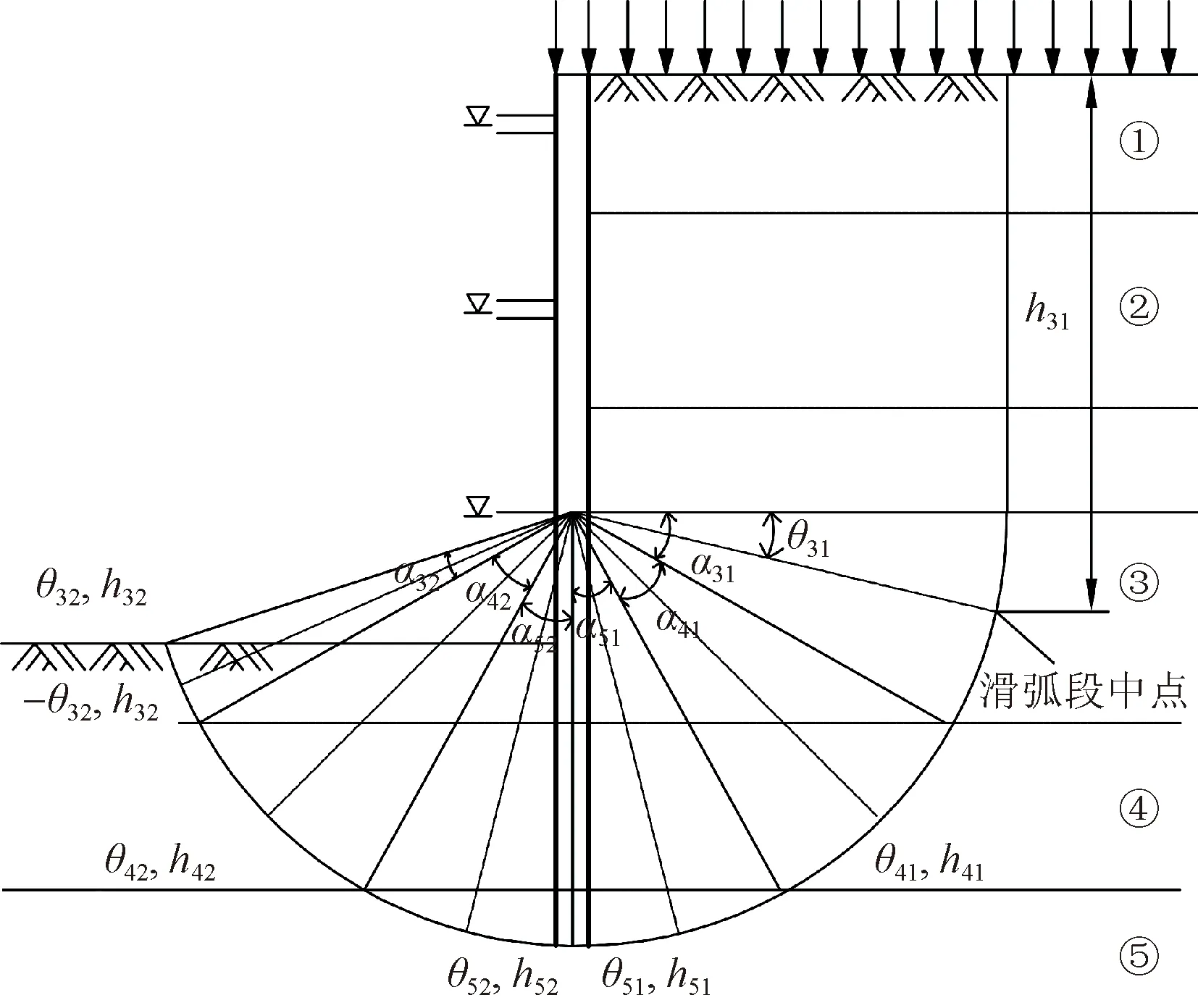
α31、α32分別為基坑外和基坑內滑弧通過第3層土的弧長對應的弧度;θ為滑弧中心點處法線方向與水平方向的夾角;h為某點處的上覆土層厚度;下角標第1個數字代表土層編號,第2個數字1和2分別代表主動區和被動區
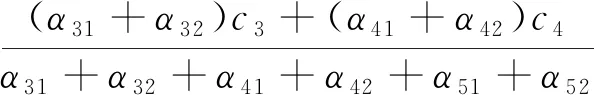
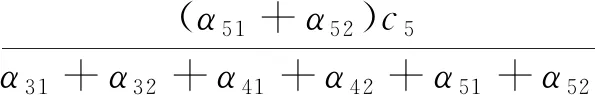
(7)
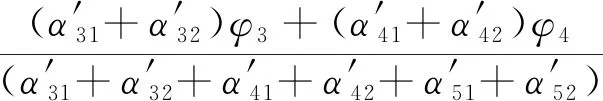
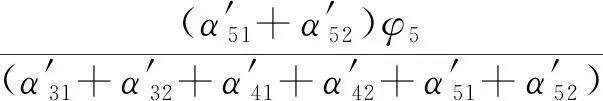
(8)
將在均質土基坑開挖條件下推導得到的加權抗剪強度指標修正值ceq、φeq代入式(9)、式(10) 中即可得到修正的抗滑力矩及滑動力矩,進一步可求得坑底抗隆起安全系數,計算得到的坑底抗隆起安全系數接近分層積分法的結果。
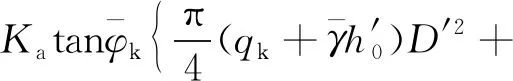
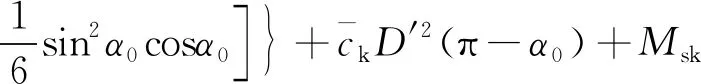
(9)
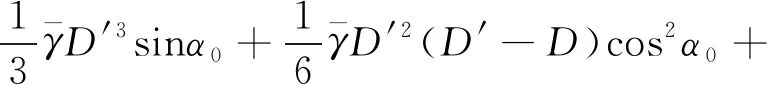
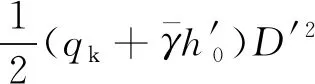
(10)
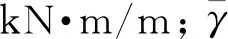
對于窄基坑坑底抗隆起穩定性的驗證,王洪新[43]通過構造新的圓弧轉動中心,如圖4所示,提出的改進計算方法會使抗滑力矩與滑動力矩均多出一個附加項如式(11)、式(12)所示。
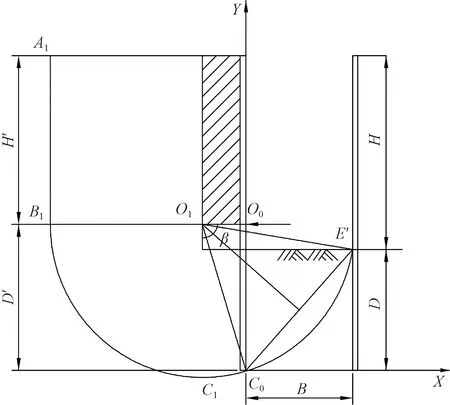
D′為最下道支撐距離圍墻底的垂直距離;H′為最下道支撐點距地面的深度;β為O1C0與水平面的夾角;B為基坑開挖寬度
滑動力矩計算公式中應減去修正項[式(11)],則有
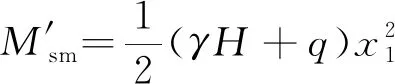
(11)
抗滑力矩計算公式中應加上修正項[式(12)],則有
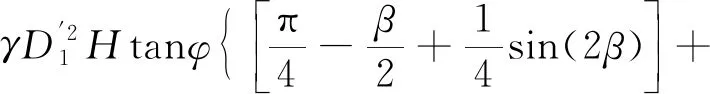
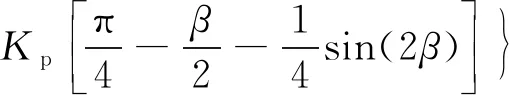
(12)
式中:Kp為被動土壓力系數;x1為最下道支撐延長線上O1的橫坐標;D′1、sin(2β)為過渡公式。
Su等[44]、應宏偉等[16]及周建等[20]分別考慮注漿樁加固黏土深基坑、基坑開挖寬度及基坑空間效應的影響改進了傳統的坑底隆起圓弧滑動法。
總結比較了3種不同坑底隆起圓弧滑動模式改進計算方法的破壞機制、適用性、相互聯系及存在的問題,如表2所示。

表2 圓弧滑動計算方法改進匯總比較
2.3 可靠度分析
傳統的基坑抗隆起穩定確定性計算方法,得到的安全系數大于1則認為基坑坑底是穩定的。然而,由于實際基坑場地中的巖土體物理力學特性存在不確定性,即使安全系數大于1或設計規范中規定的最小值,也可能發生坑底隆起造成基坑失穩。基于此,為合理考慮基坑開挖中土體參數的不確定性,可靠度分析方法在基坑穩定性研究中被廣泛應用。概率分析使得巖土體材料的空間變異性及土體參數的不確定性可以得到充分考慮[45-47],為判斷工程設計合理性提供更多參考[48-49]。可靠度分析通過概率理論反映基坑場地土體參數,并結合預測的巖土體參數分析得到基坑隆起概率。已有學者[50-53]基于Low等[54]開發的Excel電子表格模擬不同工況下土體及圍護結構的參數特征計算可靠度指標,得到的基坑隆起破壞概率符合實際。通過對巖土體空間變異性條件下基坑隆起穩定性可靠性進行分析,發現考慮空間變異性將會導致得到更高的可靠性指標,即降低了基坑隆起的失效概率,且土層的空間變異性、波動尺寸、特征長度、滲透深度及不排水抗剪強度對可靠度指標存在顯著影響[31]。Luo等[55]提出一種基于方差縮減的抗隆起破壞可靠性設計簡化方法,并驗證了該方法在評價基坑抗隆起穩定性分析中是有效的。通過分析一系列土性指標對基坑抗隆起穩定性可靠指標的影響時,發現內摩擦角的變異性對可靠性指標的影響最大,黏聚力次之,容重影響不明顯[56]。Wu等[57]基于可靠度分析,采用圓弧滑動法研究空間變異性對坑底抗隆起安全系數的影響,結果表明考慮空間變異性的抗隆起安全系數比不考慮空間變異性時要小得多。Zhou等[58]表明基坑抗隆起安全系數與其破壞風險高低并無決定性關系;相同安全系數的坑底隆起風險也不同[59]。可以看出,可靠度理論為基坑抗隆起穩定性分析提供了一種有效研究方法。
3 復雜基坑坑底抗隆起穩定性研究
3.1 圓形基坑抗隆起穩定性研究
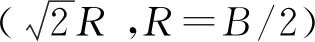
3.2 坑中坑式基坑抗隆起穩定性研究
超高層建筑物、城市地下空間綜合體、地鐵換乘車站等重要地下工程中的基坑往往以坑中坑的形式出現[71-73],這種對基坑進行二次開挖形成的坑中坑形式基坑對原基坑的抗隆起穩定性會造成一定影響[74-75],為此,眾多學者對坑中坑基坑抗隆起穩定性進行了分析。鄭俊星等[76]認為內坑的開挖會削弱外坑的被動區,從而降低外坑的抗隆起穩定性,同時根據內外坑的水平距離d將內坑的削弱效應分為兩種,即d是否大于圓弧滑裂面與坑底的交點到圍護結構的距離d1,當d≥d1時,繼續增大d對坑底抗隆起安全系數的影響較小且趨近與單一基坑開挖的安全系數;當d qf為BP處荷載;W為內外坑間距;Hw為外坑圍護結構長度;He為外坑開挖深度;Hp為外坑圍護結構嵌固深度;Hs為外坑最下道內支撐深度;H′e為內坑開挖深度;Struct 1、Struct 2、Struct 3、Struct 4、Struct 5分別為內支撐1、2、3、4、5;O為圓弧滑裂面的圓心;R為圓弧滑裂面的半徑;A、B、C、D、E、F、G為確定滑裂面的點;J為支擋結構頂部與外坑地面相交的點;P為外坑最下道支撐與支擋結構交點;K為外坑坑底與支擋結構交點;M、N分別為內坑坑頂及坑底與支擋結構的交點;A′、E′、d、E′等分別為圖中對應的角度 隨著地下空間開發規模的擴大,基坑工程面臨越來越多的穩定性問題,如何保證基坑穩定、減少風險是基坑工程設計中重要環節。總結了基坑寬度、土體各向異性及連續墻入土深度等關鍵設計因素對基坑坑底抗隆起穩定性的影響,基坑越窄、土體各向異性比越低及支擋結構嵌固段越深對基坑坑底抗隆起穩定性越有利。對目前基坑坑底抗隆起穩定性驗算方法的兩種極限平衡方法改進后的計算方法及工況進行總結,改進后的計算方法在復雜工況下的計算結果更接近實際監測值;考慮土體參數空間變異性的可靠度分析方法在基坑坑底隆起失效概率計算中更為合理。坑中坑式基坑的開挖相較于單一基坑的開挖更為復雜,內外坑間距決定坑中坑式基坑存在內部型和外部型坑底隆起破壞機制,其抗隆起穩定性的驗算與內坑開挖位置有很大關聯,其中外部型坑中坑可按單一基坑分析其抗隆起穩定性。 通過分析基坑抗隆起穩定性研究的新進展, 相應地提出研究可能面臨的以下重點難點問題。 (1)已有研究多考慮下臥層為軟土層或水平硬層,對于大型基坑坑底可能存在的不規則或傾斜地層工況,實際地層分布條件對基坑抗隆起穩定性研究還需要深入;建于城市密集區的基坑工程,如何考慮周圍環境與坑底隆起間的相互作用至關重要。 (2) 坑底抗隆起穩定性問題屬于三維穩定性問題,現有研究多以平面應變分析為主,研究方法需要進一步改進;運用可靠度分析方法得到的基坑抗隆起失穩的概率標準目前尚未統一。 (3) 對于如圓形基坑、橢圓形基坑、坑中坑式基坑等特殊形式的基坑,由于其獨特的截面特性,坑底隆起破壞機制不同于傳統的方形基坑,尚未見適用的抗隆起穩定性分析方法。 (4) 現有基坑抗隆起穩定性分析多以坑底最后破壞為標準,忽視了坑底隆起的發展過程,特別是對于中國東部軟土地區,基坑設計時常忽略了軟土的流變特性,因此,有必要考慮滲流效應和土體流變性對基坑抗隆起穩定性的影響。 (5) 針對坑底隆起這一安全風險,亟待建立集精細化風險辨識、定量化風險分析、動態化風險評估、自動化風險監測預警、智能化風險決策響應于一體的風險管理技術體系及安全風險預警、智慧防控體系,完善基坑工程風險防控機制,健全應急管理體系,促進在建基坑工程建設本質安全及智慧風險科技進步。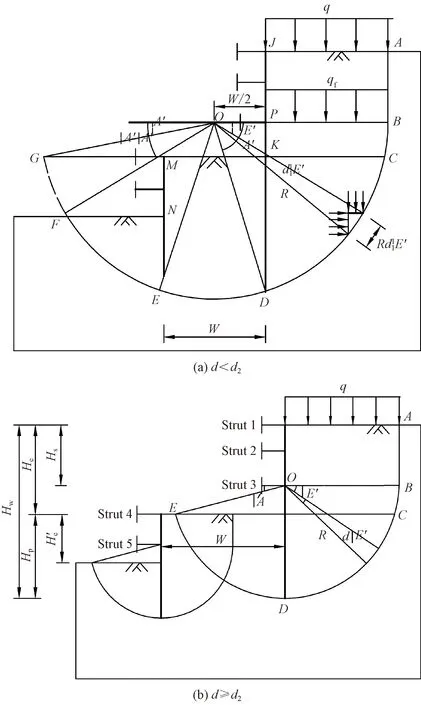
4 結論與展望

