包殼管三維力學建模及其變形分析軟件開發

張明， 厲井鋼， 劉虓瀚， 盧勇， 朱亞楠

(中廣核研究院有限公司反應堆工程軟件研究所， 深圳 518000)

燃料棒包殼是防止放射性物質外泄的第一道安全屏障，其堆內性能直接影響核電廠運行的安全性與經濟性。因此，燃料棒包殼的變形機理及其數值分析方法一直是反應堆核燃料研究的重點。

燃料棒包殼一般由鋯合金[1]制成，在壽命初期由于UO2芯塊的密實作用其體積收縮，導致包殼在軸向產生未支撐段，這是包殼蠕變坍塌的先決條件。在反應堆內高溫、高壓和輻照等耦合作用下，未支撐段包殼會逐漸向內蠕變，最終坍塌失效，蠕變是包殼坍塌的根本原因。包殼坍塌會造成局部熱點影響冷卻劑流道，或者使得臨近燃料棒或導向管彎曲，影響反應堆運行安全。中國壓水堆燃料組件設計標準[2]規定：包殼要滿足自立條件，且不能發生蠕變坍塌。由于包殼的服役工況復雜，難以直接觀測其變形狀態，因此需要對包殼的變形和應力進行建模計算，常見分析方法包括理論解析建模和開發專用軟件求數值解。

包殼管的理論建模可追溯到1959年，Hoff等[3]研究了無限長薄圓柱殼在均勻外壓作用下的穩態蠕變行為，但未考慮包殼管的彈塑性變形和瞬態蠕變。Bargmann[4]通過考慮彈性變形擴展了Hoff的方法，并指出包殼的彈性變形會極大降低包殼壽命。Nishiguchi[5]假設應力沿著壁厚均勻分布，并給出無限長高溫氣冷堆加熱管的蠕變坍塌臨界時間。以上研究只限于模態二失穩，并未考慮失穩后的后屈曲行為。隨后，嚴愛民[6]提出了高溫和外壓作用下有限長圓柱殼的多模態蠕變失穩解法；謝旭華[7]開展了無限長夾心殼的后屈曲研究；Xue[8]研究了無限長圓柱薄殼的局部失穩現象，并給出了其后屈曲解；盧勇等[9]基于商業有限元軟件ABAQUS研究了三維燃料棒包殼管的變形和坍塌行為。

雖然理論建模可得到包殼管蠕變失穩和后屈曲的解析解，但理論建模只適用于邊界規則、幾何模型簡單的問題，對于堆內變形行為復雜的包殼管，通常開發專用數值軟件計算包殼的堆內狀態，并判斷其是否符合安全標準。常見的包殼變形分析軟件包括BUCKLE[10]、COLAPX[11]、COVE-1[12]、CEPAN[13]和FROCO[14]等，以上軟件采用無限長管假設(即平面應變假設)和截面上的對稱假設，在蠕變坍塌變形計算和臨界壽命評估方面存在以下不足。

(1)均基于平面應變假設，是一種二維的力學模型，其幾何模型為無限長管，這在變形分析中會產生較大誤差，雖然COVE-1[12]、CEPAN[13]和FROCO[14]考慮了對有限長管的修正，但計算誤差仍然較大。

(2)COLAPX[11]、COVE-1[12]、CEPAN[13]和FROCO[14]在截面內采用對稱假設，只分析1/4模型，故只能分析圓管變為橢圓管的模態二失穩，而實際包殼未支撐段為有限長度，一般會發生多模態失穩[8]，以上軟件無法準確模擬。

(3)在數值計算方法方面，BUCKLE[10]、COVE-1[12]和CEPAN[13]采用有限差分法，計算精度依賴于空間和時間步長，大時間步長的計算結果精度受限；FROCO[14]采用矩陣變換法將計算域離散為許多小結塊，未考慮結塊之間的相互作用，難以精確得到包殼的變形和應力狀態。綜上所述，現有計算軟件的基本假設和計算方法不盡合理，難以精確計算包殼的應力和變形，也難以準確預測包殼的堆內狀態。盡管商業軟件在包殼管蠕變變形計算中可以被采用[9]，但其仍不如以上專業軟件應用廣泛和計算方便。

針對現存軟件的不足，亟須研究燃料棒包殼的三維變形機理，即建立熱-輻照-力等多物理場耦合作用下的包殼模型，并開發出高精度的專用計算軟件。現基于連續介質力學力學理論建立包殼管的控制方程，引入相應的蠕變本構關系，并開發基于有限元的包殼管三維變形數值計算方法。通過與商業軟件ABAQUS結果的對比來驗證本軟件的正確性，并計算真實燃料棒包殼的堆內變形。

1 方法

1.1 控制方程

直接建立包殼管的三維幾何模型，無需要求包殼管滿足平面應力/應變假設。笛卡爾坐標系下一般彈性體的力學控制方程如下。

(1)平衡方程

(1)

式(1)中：σ為應力；x為坐標，i,j=1、2、3分別表示x、y、z方向。式(1)展開為3個方程。

(2)幾何方程

(2)

式(2)中：ε為應變；x為坐標；u為位移。式(2)展開為6個方程。

1.2 彈性本構關系

對于彈性體，要想計算出其位移，必須給出彈性本構關系，這里假設包殼管在彈性階段為線彈性材料，其應力應變關系符合廣義胡克定律，即

σij=2Gεij+λεkkδij

(3)

式(3)中：G=E/[2(1-ν)]為剪切模量；λ=Eν/[(1+ν)(1-2ν)]為體積模量，E為彈性模量，ν為泊松比；εkk為體積應變。式(3)包含6個方程。

一般地，彈性力學方程式(1)～式(3)共包含15個方程，需要求15個未知數，分別為應力6個、應變6個和位移3個，因此以上3組方程是封閉的方程系統。引入包殼管的蠕變本構方程，增加方程的同時也增加了蠕變相關的未知量，故方程系統還是封閉、適定的。

1.3 蠕變本構關系

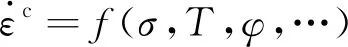
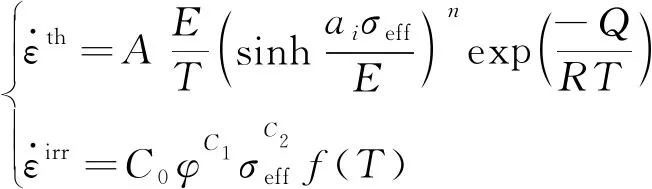
(4)

式(4)中：σeff為等效應力；T為溫度；φ為中子注量率，其他參數的取值見表1。參考塑性力學理論的Prandtl-Reuss流動法則，將等效蠕變應變流動到各個方向，即

表1 蠕變本構模型中的材料參數[15]

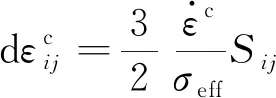
(5)

式(5)中：Sij為偏應力。

1.4 有限元計算方法

以上方程不僅個數多，而且涉及蠕變引起的材料非線性，無法直接求解，故對以上控制方程進行有限元離散。將有限長的包殼管離散為六面體，采用八節點線性等參元建模。為了兼顧效率和精度，經網格收斂性測試后包殼管徑向、環向和軸向的網格數分別為3、40和7個，總網格數為840，結構化網格劃分如圖1所示。

圖1 包殼管三維網格

八節點等參元的形函數為

(6)

式(6)中：ξ、η、ζ分別為母單元上的3個方向的坐標值。

單元內任一點的坐標和位移可以用8個節點的相應量插值表示為

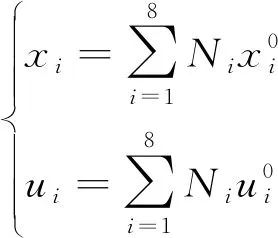
(7)

式(7)中：帶有上角標“0”的量均表示結點的值。

將應變張量寫為Voigt向量的形式，并把式(7)中位移代入幾何方程[式(2)]，則應變向量為

ε=Bu0

(8)

式(8)中：B為應變矩陣。

應力的向量形式由式(3)得到，即

σ=Dε=DBu0

(9)

式(9)中：D為彈性矩陣。

將蠕變應變看作初應變，忽略重力引起的體積力，根據虛功原理，可得有限元方程為

Keu0=fl+fc

(10)

Ktu0t=flt+fct

(11)

通過高斯消去法或超松弛迭代(successive over-relaxation, SOR)法即可計算t時刻的位移。下一時刻t+Δt先由式(4)和式(5)計算蠕變應變，得到附加載荷列陣，再計算載荷向量，重新求解式(11)即得到下一時刻的位移，以此類推直至燃料棒包殼的壽期末。

1.5 包殼失效準則

為了預測包殼管服役狀態，并判斷其是否失效，需要建立包殼管的蠕變坍塌準則，擬采用以下的失效準則。

(1) 最大屈服應力準則。當應力達到包殼管的屈服應力時，認為包殼失效[2]。

(2) 最大橢圓度準則和最大位移準則。當包殼管上任一點的橢圓度或位移超過限值時，認為包殼蠕變坍塌，橢圓度限值取25%[10]，最大位移的限值取包殼管最小外徑的一半[14]。

2 結果與討論

2.1 測試和驗證

為了驗證自主軟件BINE3D的正確性，擬采用相同的模型與商業軟件ABAQUS對比。分別從靜力結果和蠕變結果兩方面對自主軟件進行測試與驗證。

2.1.1 靜力測試

如圖2所示，考慮一邊長為1×1×1的立方體，在一個面受到均勻外部拉力1，材料的彈性模量為1、泊松比為0.346，理論結果、ABAQUS和本軟件結果見表2。

表2 靜力結果對比

圖2 單元示意圖

對比可看出，軟件結果與理論解和ABAQUS結果相同，BINE3D計算結果正確。

2.1.2 蠕變測試

仍采用2.1.1節的模型和參數，同時將蠕變引入，因ABAQUS軟件未提供蠕變本構模型[式(4)]，故用經典Norton本構模型代替。Norton蠕變本構的表達式為

(12)

式(12)中：常數A=0.000 713 05，n=0.8，m=-0.991 5。

BINE3D結果和商業軟件ABAQUS結果如圖3所示。

圖3 單元蠕變結果對比

可以看出，BINE3D結果和ABAQUS結果重合，具有一致性，從而驗證了BINE3D計算結果的準確性。

2.2 包殼管結構蠕變坍塌分析

測試和驗證表明BINE3D可用于考慮蠕變效應的三維包殼管變形分析。擬進行一真實工況下包殼管的變形分析,包殼管外徑為9.75 mm，厚度為0.57 mm，軸向高度為100 mm，彈性模量為絕對溫度的函數，即E=1.149×105-59.9T，泊松比為0.346，蠕變本構方程為式(4)，包殼兩端位移固定，堆內輻照參數取一典型工況下的溫度史、壓力史和中子注量史。

包殼截面為均勻圓管時，其最大位移隨著時間變化曲線見圖4。可以看出，隨著包殼管輻照時間的增加，因蠕變產生位移逐漸增加，并且位移的增加速度逐漸減小。到60 000 h，最大位移為0.006 81 mm，包殼結構未失效。

圖4 包殼管最大位移隨時間變化曲線

不同初始橢圓度下三維包殼管一中部截面(高度h=42.875 mm)的橢圓度隨時間變化規律見圖5，隨著服役時間的增加，初始橢圓度較大的包殼管總橢圓度也較大。隨著輻照時間的增加，包殼橢圓度增加速度逐漸減小。輻照60 000 h時，初始橢圓度為0.1 mm的包殼最大橢圓度為3.91%，遠小于限值25%，未在服役期間出現坍塌。

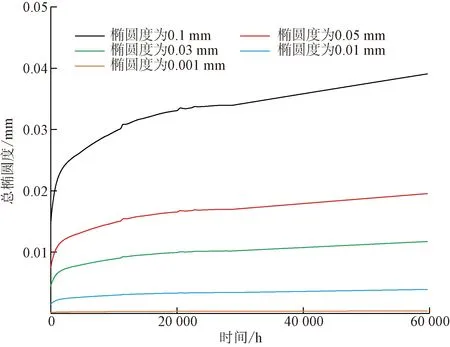
圖5 包殼管初始橢圓度對總橢圓度的影響

當橢圓度為0.1 mm時，不同時刻包殼管一中部截面(高度h=42.875 mm)外輪廓見圖6，隨著輻照時間的增加，受外壓和持續蠕變導致包殼管的位移越來越大。其長軸向外變形、短軸向內變形。

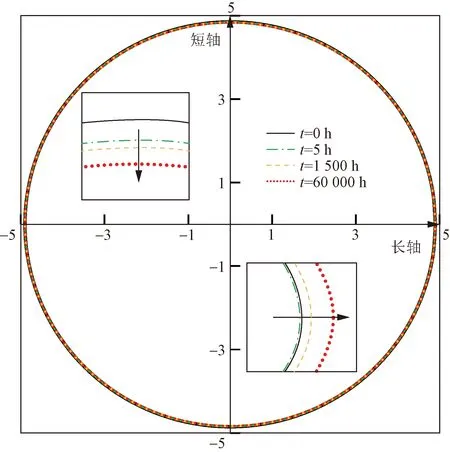
圖6 初始橢圓度為0.1 mm時，包殼管中間截面外輪廓圖

三維變形分析軟件BINE3D不需對軸向變形做出假設，也無需對包殼的變形進行修正，計算出的結果即為包殼的真實變形。隨著輻照時間的增加，長軸和短軸處軸向節點的位移見圖7。當輻照時間為60 000 h時，長軸位移呈現出兩端為負、中間為正的特點，這是由包殼的三維結構導致的。60 000 h時，長軸最大正向位移和負向位移分別為0.002 88 mm和-0.004 mm。而基于平面應變假設的修正方法無法精確修正出此結果。短軸位移一直為負，即短軸處向包殼內變形，當輻照時間為60 000 h時，最大位移為-0.016 7 mm，短軸位移較長軸大。

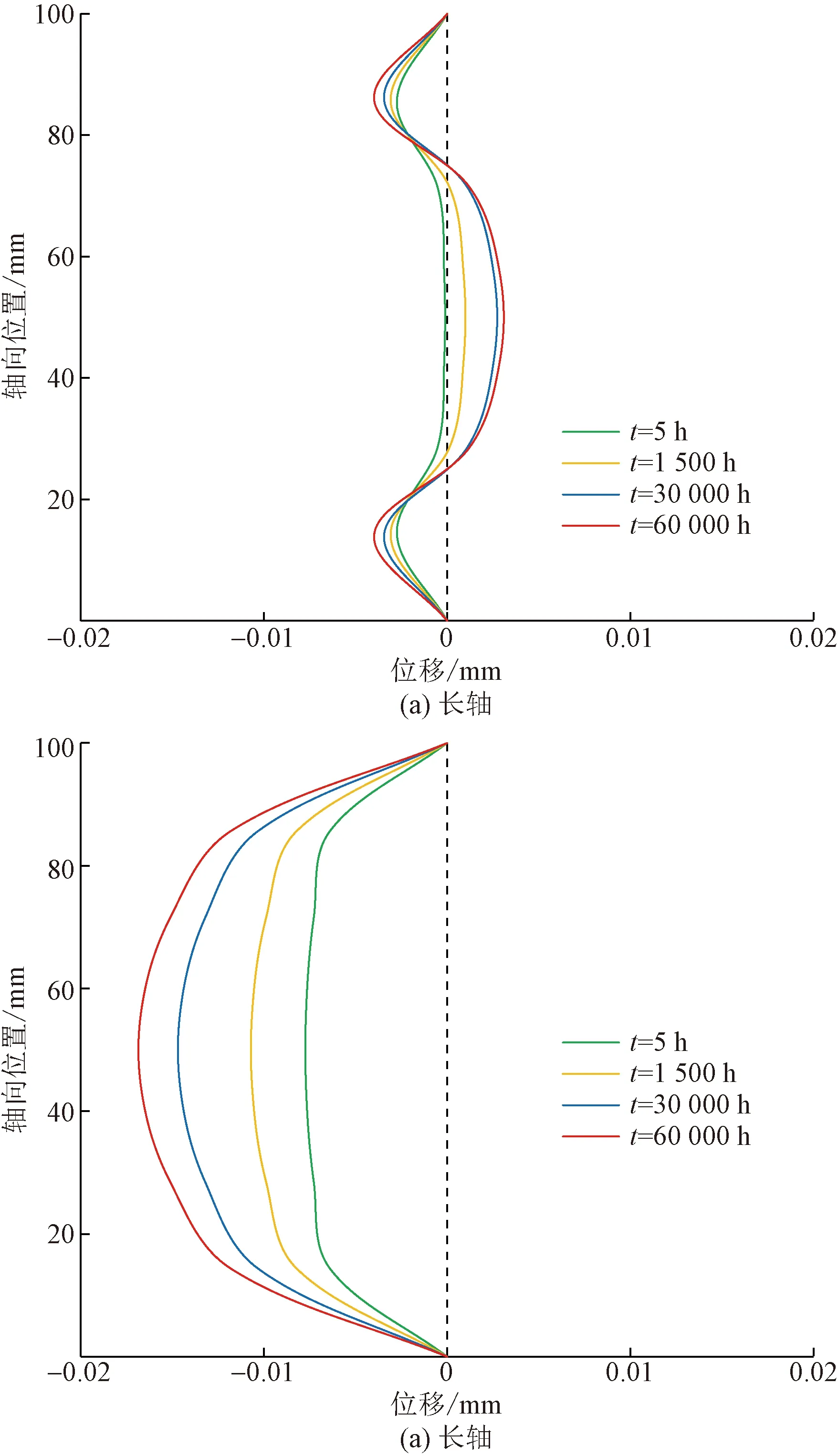
圖7 橢圓度為0.1 mm時，包殼管長軸和短軸處軸向位置的位移隨時間變化

3 結論

基于連續介質力學模型對燃料棒包殼進行了三維力學建模，并采用有限元方法開發出了包殼三維變形分析軟件BINE3D，可用于預測包殼的堆內變形行為并揭示包殼的失效機理。主要工作和結論如下。

(1) 基于有限元數值方法開發了燃料棒包殼三維變形分析軟件BINE3D，可準確預測包殼三維在堆變形狀態。

(2) 包殼的變形速度(主要由蠕變導致)隨著輻照時間的增加逐漸減小。

(3) 具有橢圓截面的三維包殼結構，其長軸位移有正有負，而短軸位移均為負且較長軸的變形量較大。

(4) 該軟件有望對其他復雜結構的核燃料包殼進行分析。