水力壓裂多裂縫擴(kuò)展的近場動力學(xué)模擬

曹楷楠， 胡志明， 端祥剛， 常進(jìn)

(1.中國科學(xué)院大學(xué)工程科學(xué)學(xué)院， 北京 100049； 2. 中國科學(xué)院滲流流體力學(xué)研究所， 廊坊 065007； 3.中國石油勘探開發(fā)研究院， 北京 100083)

為了解決水力壓裂裂縫起裂與擴(kuò)展中的力學(xué)問題，一般采用理論分析、實驗方法和數(shù)值模擬方法。常用的數(shù)值模擬方法包括有限元方法、邊界元法、擴(kuò)展有限元方法等[1]，是基于連續(xù)介質(zhì)力學(xué)理論，將裂縫的擴(kuò)展看作裂縫內(nèi)壓裂液流動和巖體斷裂變形的耦合問題。連續(xù)介質(zhì)理論假設(shè)物質(zhì)點只和相鄰的物質(zhì)點有相互作用，近場動力學(xué)基于非局部理論，即物質(zhì)點和近場范圍內(nèi)的所有物質(zhì)點均有相互作用，以積分方程代替微分方程，不需要空間求導(dǎo)，便于處理材料裂紋擴(kuò)展中的不連續(xù)問題。Agwai等[2]將宏觀上描述裂紋擴(kuò)展的擴(kuò)展有限元方法(extend finite element method，XFEM)與近場動力學(xué)(peridynamics，PD)做比較，結(jié)果發(fā)現(xiàn)近場動力學(xué)得到的結(jié)果與實驗結(jié)果更接近，可以看到分叉行為與微觀分叉行為。

近場動力學(xué)由Silling[3]提出，以位移的空間積分形式重構(gòu)了傳統(tǒng)連續(xù)介質(zhì)理論，這種積分形式實現(xiàn)了對連續(xù)介質(zhì)和非連續(xù)介質(zhì)的統(tǒng)一描述，因此，近場動力學(xué)能很方便地描述材料中裂紋萌生和擴(kuò)展。近場動力學(xué)尺度介于分子尺度與宏觀尺度之間，兼具分子動力學(xué)和宏觀連續(xù)介質(zhì)力學(xué)的優(yōu)勢。分子動力學(xué)可以處理宏觀尺度下的不連續(xù)問題，但是卻難以實現(xiàn)大尺度的仿真預(yù)測，近場動力學(xué)可以彌補這一缺點[4]。

近場動力學(xué)目前廣泛應(yīng)用于材料的斷裂及裂紋擴(kuò)展預(yù)測上，在水力壓裂裂縫擴(kuò)展的問題上應(yīng)用較少。頁巖儲層水力壓裂裂縫擴(kuò)展問題為裂縫內(nèi)流體流動與巖石固體變形的流固耦合問題。中外研究人員借助近場動力學(xué)研究了水力壓裂中的流固耦合問題，Turner[5]基于近場動力學(xué)建立了多孔介質(zhì)滲流過程的流固耦合模型。吳凡等[6]通過鍵基的近場動力學(xué)理論，采用等效壓力解決流固耦合問題，建立了二維的水力壓裂模型；張鈺彬等[7]通過常規(guī)態(tài)基的近場動力學(xué)理論，建立了平面二維的水力壓裂模型。Ouchi等[8]基于常規(guī)態(tài)基近場動力學(xué)，建立了水力壓裂模型，對水力裂縫與天然裂縫的相互作用進(jìn)行了較為詳細(xì)的研究。Nadimi等[9]通過近場動力學(xué)理論較為詳細(xì)地研究了水力裂縫與天然裂縫的交互作用，并對排量等施工參數(shù)的影響進(jìn)行不同結(jié)果的比較。Qin等[10]提出一種新的近場動力學(xué)模型和方法用于解決水力壓裂問題。Zhou等[11]建立了近場動力學(xué)的流固耦合模型，應(yīng)用到水力壓裂問題中。近場動力學(xué)理論用于水力壓裂的優(yōu)勢在于，通過描述物質(zhì)點之間鍵的連接情況，可以自動捕捉到裂紋的擴(kuò)展，不足之處在于物質(zhì)點之間的間距有限制，不適用于大尺度仿真，通過耦合有限元方法可以解決這一問題[12]。

水平井技術(shù)和水力壓裂技術(shù)是目前頁巖氣開發(fā)的主要技術(shù)手段，目的在于形成復(fù)雜縫網(wǎng)，提高頁巖氣采出程度。在頁巖氣的壓裂過程中，通常要進(jìn)行多簇射孔和多簇壓裂，裂縫間會存在干擾，中外對多裂縫干擾問題的研究方法大多采用基于擴(kuò)展有限元法及位移不連續(xù)法等[13-15]，現(xiàn)以水力壓裂問題為研究背景，基于近場動力學(xué)理論，設(shè)計水力壓裂多裂縫擴(kuò)展的數(shù)值算例，預(yù)期從非局部理論的角度得到對多裂縫擴(kuò)展規(guī)律的認(rèn)識。

1 近場動力學(xué)運動方程及數(shù)值離散

Silling等[16]在鍵基近場動力學(xué)理論的基礎(chǔ)上，提出態(tài)基近場動力學(xué)理論，可以更好地描述物體的變形。態(tài)基近場動力學(xué)的運動方程一般可以表示為

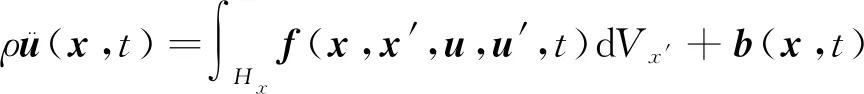
(1)

f=T[x,t]〈x′-x〉-T[x′,t]〈x-x′〉

(2)

式中：ρ為材料密度；x為物質(zhì)點的位置矢量；u(x,t)為物質(zhì)點位移；Hx為點x的近場范圍；f為物質(zhì)點之間的相互作用力函數(shù)，稱為本構(gòu)力函數(shù)；T[x,t]為力態(tài)；b(x,t)為體力；Vx′為鄰點體積。近場動力學(xué)通過鍵的拉伸破壞描述物體的損傷和斷裂，采用伸長率s表征鍵的拉伸程度，表達(dá)式為

(3)

式(3)中：ξ為鍵長；η為相對位移。當(dāng)伸長率大于臨界伸長率s0時，鍵斷裂，對于平面應(yīng)力問題[17]，有

(4)

(5)

(6)

采用無網(wǎng)格方法直接離散得到物質(zhì)點運動方程的空間離散化形式為

(7)

對于時間離散采用Velocity-Verlet方法，該方法相較于直接向前差分法，有較好的穩(wěn)定性。該方法采用的積分形式為

(8)

2 流固耦合方法

2.1 固體域變形描述

對固體域直接采用近場動力學(xué)運動方程的離散形式，離散為一系列物質(zhì)點，物質(zhì)點存儲位移，質(zhì)量密度，體力密度等物理量信息。

對流體域，基于連續(xù)介質(zhì)力學(xué)觀點建立滲流控制方程，采用有限差分法進(jìn)行離散，固體域和流體域共用同一套離散網(wǎng)格點，并依據(jù)有效應(yīng)力原理，將裂縫和孔隙中的水壓力添加到固體域物質(zhì)點間的力態(tài)中，實現(xiàn)流固耦合過程。

Biot[18]引入有效應(yīng)力系數(shù)，將有效應(yīng)力原理應(yīng)用范圍由土力學(xué)擴(kuò)展到巖土力學(xué)。對于多孔介質(zhì)的有效應(yīng)力，可以表示為

σtotal=σeff+αPI

(9)

式(9)中：σtotal為總應(yīng)力張量；σeff為有效應(yīng)力張量；α為Biot固結(jié)系數(shù)；P為孔隙壓力；I為單位張量。通過損傷值大小劃分連續(xù)空間，損傷無斷裂空間與損傷斷裂空間，分別對應(yīng)3種鍵的力態(tài)。

(1)無損傷連續(xù)空間連續(xù)鍵力態(tài)。無損傷連續(xù)空間中物質(zhì)點對之間的鍵未斷裂，即物質(zhì)點的損傷值為0，在平面應(yīng)力問題的力態(tài)基礎(chǔ)上[19]，得到物質(zhì)點連接鍵上的力態(tài)為

(10)

(2)損傷無斷裂空間斷裂鍵力態(tài)。當(dāng)物質(zhì)點對之間發(fā)生損傷，但是物質(zhì)點損傷值沒有超過臨界損傷程度時，物質(zhì)點處于損傷無斷裂空間，物質(zhì)點之間的力學(xué)項消失，但是孔隙壓力項仍然保留，物質(zhì)點之間的斷裂鍵上的力態(tài)為

(11)

(3)損傷斷裂空間的斷裂鍵力態(tài)。將損傷值及鄰對點損傷值均超過臨界損傷值，且鍵為拉長狀態(tài)的物質(zhì)點作為損傷斷裂空間的物質(zhì)點[20]，將水力壓力以非局部形式作用在物質(zhì)點上，則損傷斷裂空間的物質(zhì)點之間的斷裂鍵上的力態(tài)為

(12)

式(12)中：Pf為壓裂液在裂縫面上的壓力。

2.2 流體域壓力描述

將流體域劃分為裂隙區(qū)、基質(zhì)區(qū)及過渡區(qū)，對應(yīng)固體域變形描述中的損傷斷裂空間，無損傷連續(xù)空間及損傷無斷裂空間。

對于裂隙區(qū)的物質(zhì)點，認(rèn)為壓力值近似為注入壓力。對于基質(zhì)區(qū)和過渡區(qū)的物質(zhì)點，采用連續(xù)介質(zhì)觀點描述流體流動，物質(zhì)點流動規(guī)律采用達(dá)西定律描述為

(13)

式(13)中：P為壓力；μf為流體黏度；K為滲透率張量；對于各向同性的連續(xù)空間采用基質(zhì)滲透率Kr、損傷斷裂空間采用裂隙滲透率Kf和損傷無斷裂空間滲透率Ks通過損傷程度取平均值獲得，即

Ks=φKf+(1-φ)Kr

(14)

式(14)中：φ為物質(zhì)點的損傷值。對于均勻各向同性介質(zhì)，假設(shè)基質(zhì)孔隙度不變，得到滲流控制方程[21]簡化后的結(jié)果為

(15)

對于式(15)的控制方程，采用有限差分法對壓力項和源項進(jìn)行離散，采用顯式差分格式對時間項離散，控制方程中的參數(shù)K、φ、ci、μf均為常數(shù)，于是得到二維直角坐標(biāo)下離散后的控制方程為

(16)

最后，借助C++工具和OpenMP并行框架實現(xiàn)流固耦合過程。

3 研究內(nèi)容

3.1 模型及參數(shù)

設(shè)置模型尺寸為1.0 m×1.0 m，計算域內(nèi)共劃分10 000個物質(zhì)點，其中水平方向和豎直方向分別劃分100個物質(zhì)點，物質(zhì)點間距為0.01 m，近場范圍取物質(zhì)點間距的3倍，為0.03 m，邊界厚度取近場范圍大小，巖石彈性模量為5 GPa，巖石泊松比為0.333，巖石密度為3 400 kg/m3，流體密度為1 000 kg/m3，裂隙滲透率為1.333×10-3mD，基質(zhì)滲透率為1×10-12mD，巖石材料孔隙度為0.5，Biot固結(jié)系數(shù)為0.5，綜合壓縮系數(shù)為1，將臨界損傷程度設(shè)置為0.39[10]，即認(rèn)為當(dāng)物質(zhì)點和相鄰物質(zhì)點的損傷程度均大于0.39時，物質(zhì)點和相鄰物質(zhì)點位于裂縫的兩側(cè)，時間步長取0.000 001 s。模型邊界設(shè)置為位移約束，邊界四周固定，壓力邊界設(shè)置為透水邊界，邊界處壓力為零。設(shè)置裂縫中心為壓力注入點，預(yù)置裂縫內(nèi)壓力隨時間勻速增加，壓力增速為10 000 MPa/s。

為了研究縫間的干擾作用對多裂縫擴(kuò)展規(guī)律的影響，設(shè)計了如圖1所示的4組數(shù)值模型實驗，其中，圖1(a)為間距0.1 m的兩條平行對齊裂縫，兩條裂縫長度為0.1 m；圖1(b)為間距0.2 m的兩條平行對齊裂縫，與圖1(a)對比，觀察不同裂縫間距下的結(jié)果；圖1(c)為兩條平行交錯裂縫，兩條裂縫間距為0.1 m，兩條裂縫長度為0.1 m；圖1(d)為三條平行對齊裂縫，裂縫間距為0.2 m，裂縫長度為0.1 m。

圖1 模型初始損傷

3.2 結(jié)果及分析

3.2.1 間距不同的兩條平行對齊裂縫

圖2所示為間距0.1 m的兩條裂縫擴(kuò)展后的損傷、壓力和垂向位移。

圖2(a)表明，當(dāng)兩條水平對齊的裂縫同時擴(kuò)展后，由于裂縫間的應(yīng)力干擾，兩條裂縫呈一定角度向著相反的方向偏轉(zhuǎn)；圖2(b)表明，水壓力分布在裂縫內(nèi)，作為裂縫擴(kuò)展延伸的牽引力；圖2(c)表明，兩條裂縫內(nèi)側(cè)的物質(zhì)點垂向移動受到限制，而在兩條裂縫外側(cè)的物質(zhì)點垂向移動未受到限制。

圖2 間距0.1 m兩條裂縫擴(kuò)展結(jié)果

出現(xiàn)兩條裂縫向相反方向偏轉(zhuǎn)現(xiàn)象的原因如下。

(1)對于上側(cè)裂縫，上側(cè)裂縫物質(zhì)點與下方基質(zhì)物質(zhì)點的間距減小，下方基質(zhì)物質(zhì)點作用在上側(cè)裂縫物質(zhì)點方向向上的作用力增大，導(dǎo)致上側(cè)裂縫向上方偏轉(zhuǎn)。

(2)同理，對于下側(cè)裂縫，下側(cè)裂縫物質(zhì)點與上方基質(zhì)物質(zhì)點的間距減小，上方基質(zhì)物質(zhì)點作用在下側(cè)裂縫物質(zhì)點方向向下的作用力增大，導(dǎo)致下側(cè)裂縫向下方偏轉(zhuǎn)。

圖3所示為間距0.2 m的兩條裂縫擴(kuò)展后的損傷、壓力和垂向位移。圖3(a)表明，當(dāng)裂縫間距增加為0.2 m時，裂縫偏轉(zhuǎn)角變小。

圖3 間距0.2 m兩條裂縫擴(kuò)展結(jié)果

3.2.2 兩條平行交錯裂縫

圖4所示為兩條交錯裂縫擴(kuò)展后的損傷、壓力和垂向位移。

圖4(a)表明，當(dāng)兩條交錯水力裂縫同時擴(kuò)展時，由于裂縫間的應(yīng)力干擾，兩條水力裂縫會“互相吸引”，即兩條裂縫彼此靠近的一端會向另一條裂縫偏轉(zhuǎn)，與文獻(xiàn)[14]中的現(xiàn)象吻合；圖4(b)表明，水壓力分布在裂縫內(nèi)，作為裂縫擴(kuò)展延伸的牽引力；圖4(c)表明，兩條裂縫兩側(cè)物質(zhì)點的垂向移動會產(chǎn)生干擾。

兩條水力裂縫“互相吸引”的原因如下。

在裂縫擴(kuò)展過程中，由于物質(zhì)點之間的作用力，兩條裂縫內(nèi)側(cè)的物質(zhì)點在水平方向上的移動會受到限制，位于中心區(qū)域的物質(zhì)點由于應(yīng)力干擾，會處于受力平衡狀態(tài)而不發(fā)生移動，并且會與周圍發(fā)生移動的物質(zhì)點產(chǎn)生相對位移，當(dāng)相對位移超過鍵的臨界長度后，鍵斷裂同時物質(zhì)點出現(xiàn)損傷，當(dāng)物質(zhì)點與鄰點的損傷值均超過臨界損傷程度后，將物質(zhì)點作為裂縫內(nèi)的點，裂縫會近似沿著中心平衡區(qū)域的邊界擴(kuò)展，導(dǎo)致出現(xiàn)裂縫“互相吸引”的效果。

3.2.3 三條平行對齊裂縫

圖5所示為間距0.2 m的三條裂縫擴(kuò)展后的損傷、壓力和垂向位移。

圖5(a)表明，當(dāng)3條平行對齊水力裂縫同時擴(kuò)展時，由于裂縫間的應(yīng)力干擾，中間裂縫擴(kuò)展受到限制，兩側(cè)裂縫會向相反方向偏轉(zhuǎn)；圖5(b)表明，水壓力分布在裂縫內(nèi)，作為裂縫擴(kuò)展延伸的牽引力；圖5(c)表明，裂縫兩兩之間的物質(zhì)點的垂向移動會受到限制。

上述偏轉(zhuǎn)現(xiàn)象產(chǎn)生的原因如下。

(1)對于上側(cè)裂縫，上側(cè)裂縫物質(zhì)點與下方基質(zhì)物質(zhì)點的間距減小，下方基質(zhì)物質(zhì)點作用在上側(cè)裂縫物質(zhì)點方向向上的作用力增大，導(dǎo)致上側(cè)裂縫向上方偏轉(zhuǎn)。

(2)對于中間裂縫，中間裂縫物質(zhì)點與上方基質(zhì)物質(zhì)點及下方基質(zhì)物質(zhì)點間距均減小，上方基質(zhì)物質(zhì)點作用在中間裂縫物質(zhì)點方向向下的作用力增大，限制中間裂縫物質(zhì)點向上移動；同理，下方基質(zhì)物質(zhì)點作用在中間裂縫物質(zhì)點方向向上的作用力增大，限制中間裂縫物質(zhì)點向下移動，導(dǎo)致中間裂縫向兩側(cè)擴(kuò)展均受到限制。

(3)對于下側(cè)裂縫，下側(cè)裂縫物質(zhì)點與上方基質(zhì)物質(zhì)點的間距減小，上方基質(zhì)物質(zhì)點作用在下側(cè)裂縫物質(zhì)點方向向下的作用力增大，導(dǎo)致下側(cè)裂縫向下方偏轉(zhuǎn)。

4 結(jié)論

采用基于近場動力學(xué)和有限差分法結(jié)合的方法，嘗試從非局部理論的角度對水力壓裂中多裂縫縫間干擾問題進(jìn)行模擬研究，結(jié)果表明，由于水力裂縫間的應(yīng)力干擾，得出結(jié)論主要如下。

(1)同時擴(kuò)展的兩條平行對齊裂縫向相反的方向偏轉(zhuǎn)，并且隨著裂縫間距減小，偏轉(zhuǎn)角度增大。

(2)同時擴(kuò)展的兩條平行交錯裂縫會“互相吸引”，即兩條裂縫彼此靠近的一端會向另一條裂縫偏轉(zhuǎn)。

(3)同時擴(kuò)展的3條平行對齊裂縫，兩側(cè)裂縫會向相反方向偏轉(zhuǎn)，中間裂縫的擴(kuò)展會受到限制。

根據(jù)研究結(jié)果，在實際的壓裂設(shè)計時，根據(jù)需要考慮適度增大裂縫間距，減少裂縫間的干擾，以形成復(fù)雜的縫網(wǎng)結(jié)構(gòu)，增大改造體積，提高最終采收率。