橫觀各向同性層合板理論編程實(shí)現(xiàn)與驗(yàn)證

陳州， 杜新喜， 張慎， 袁煥鑫

(1.中南建筑設(shè)計(jì)院股份有限公司， 武漢 430071； 2. 武漢大學(xué)土木建筑工程學(xué)院， 武漢 430072)

作為重要的結(jié)構(gòu)形式之一，板式構(gòu)件在幾何上的顯著特點(diǎn)是其中一個(gè)方向(厚度)的尺寸遠(yuǎn)小于其他兩個(gè)方向(長(zhǎng)度和寬度)。根據(jù)其組成材料成分的不同，它可以由同質(zhì)或異質(zhì)材料構(gòu)成，例如將多層單層板黏合在一起組成整體的結(jié)構(gòu)板(即層合板)。通常，單層板的性能與其材料及材料主軸有關(guān)。而層合板的材料力學(xué)性能，不僅取決于組成層合板的各層單層板的性能，有時(shí)還與各層單層板的鋪設(shè)方式有關(guān)。作為一種復(fù)合材料，層合板具備單層板所沒(méi)有的材料特點(diǎn)，為滿足實(shí)際生活中不同的應(yīng)用需求，工程上普遍使用層合板的結(jié)構(gòu)形式。

其中，刨花板就是一種典型的復(fù)合材料板式構(gòu)件，是將木材或非木材植物纖維原料加工成刨花(或碎料)，施加膠黏劑(和其他添加劑)，組坯成型并經(jīng)熱壓而成的一類人造板材[1]。根據(jù)其結(jié)構(gòu)不同，分為單層結(jié)構(gòu)刨花板、三層(包括多層)結(jié)構(gòu)刨花板、漸變結(jié)構(gòu)刨花板、定向刨花板、華夫刨花板、模壓刨花板等多種形式。隨著中國(guó)對(duì)先進(jìn)生產(chǎn)線的引進(jìn)與升級(jí)，以及生產(chǎn)工藝的顯著提高，近年來(lái)國(guó)內(nèi)市場(chǎng)對(duì)刨花板的需求量不斷增加，刨花板在建筑、家居、裝飾裝修等領(lǐng)域廣泛使用。

板因其特殊的幾何特點(diǎn)，通常對(duì)板式結(jié)構(gòu)的分析不采用三維有限元。隨著有限元方法的飛速發(fā)展，如何構(gòu)造合乎要求的板單元這一中心問(wèn)題，一直吸引著許多科研工作者。早在20世紀(jì)50年代末，便逐漸開(kāi)展了針對(duì)板彎曲單元的研究，大致確定了兩大類板理論有限元：基于Kirchhoff假設(shè)的薄板理論和Mindlin-Reissner中厚板理論[2]。由于薄板中要保持單元交界面上轉(zhuǎn)角的連續(xù)(C1連續(xù)性)，使得薄板單元的構(gòu)造相對(duì)困難；而基于厚板理論建立的單元，由于“剪切閉鎖”現(xiàn)象的存在，只對(duì)中厚板有效，當(dāng)板非常薄時(shí)，求得的位移趨于零。近幾十年來(lái)，大量板單元相繼被學(xué)者們提出并被構(gòu)造。其中，值得一提的是基于離散Kirchhoff理論構(gòu)造的離散Kirchhoff三角形(discrete Kirchhoff triangle，DKT)和離散Kirchhoff四邊形(discrete Kirchhoff quadrilateral，DKQ)薄板彎曲單元[3-4]，及適用于中厚板的離散剪切三角形(discrete shear triangle，DST)單元和離散剪切四邊形(discrete shear quadrangle，DSQ)單元[5]。這些單元被分別用于計(jì)算薄板及中厚板結(jié)構(gòu)時(shí)都顯示出良好的性能，在實(shí)際工程應(yīng)用中具有較高的精度。

現(xiàn)基于復(fù)合材料宏觀力學(xué)[6]分析方法，對(duì)三層結(jié)構(gòu)刨花板進(jìn)行結(jié)構(gòu)靜力試驗(yàn)及有限元數(shù)值分析。由于刨花板內(nèi)部為交叉錯(cuò)落結(jié)構(gòu)的顆粒狀材料，結(jié)構(gòu)均勻，在板平面內(nèi)各方向材料特征基本相同，而垂直此面方向的性質(zhì)不同，故采用橫觀各向同性[7-8]本構(gòu)關(guān)系對(duì)刨花板的力學(xué)性能進(jìn)行模擬。同時(shí)，對(duì)基于Kirchhoff薄板理論的DKT、DKQ薄板單元及基于Mindlin-Reissner中厚板理論的DST、DSQ中厚板單元進(jìn)行有限元編程及性能驗(yàn)證，并介紹板構(gòu)件、材料參數(shù)及節(jié)點(diǎn)位移轉(zhuǎn)角在空間內(nèi)全局坐標(biāo)系中的轉(zhuǎn)換方法。最后對(duì)比應(yīng)用不同板單元時(shí)，對(duì)有限元模型計(jì)算的影響。

1 板理論及板有限元編程

1.1 橫觀各向同性板理論

板由于在幾何上厚度尺寸遠(yuǎn)小于其他兩個(gè)方向，故簡(jiǎn)化為二維問(wèn)題可以減少計(jì)算工作量。如圖1所示，板中面為平面Oxy，不可變形的線段Mm初始時(shí)垂直于板中面于點(diǎn)m。在板變形過(guò)程中，Mm保持筆直卻不一定始終與中面垂直，即線段Mm為剛體運(yùn)動(dòng)。點(diǎn)m處的位移矢量記為u(m)，被定義為：u(m)=u(x,y)x+v(x,y)y+w(x,y)z。線段Mm繞x軸、y軸轉(zhuǎn)角分別記為-βy、βx，即轉(zhuǎn)角矢量θ=(-βy,βx, 0)。如圖2所示，則M點(diǎn)處位移矢量可表示為

h為厚度；Lx為長(zhǎng)度；Ly為寬度；L為垂直于各向同性面(T平面)方向

圖2 板內(nèi)任意線段Mm的運(yùn)動(dòng)學(xué)分析

u(M)=u(m)+Mm×θ

(1)

通常將板厚方向標(biāo)記為1或z，故采用如下的標(biāo)注方式為

(x,y,z)=(2,3,1)

(2)

板內(nèi)任意一點(diǎn)M(x,y,z)的位移場(chǎng)u(M)由式(2)所定義。可見(jiàn)，板內(nèi)位移場(chǎng)u(M)在板平面內(nèi)的兩個(gè)位移分量隨縱坐標(biāo)z(在板厚度上)線性變化，而橫向位移(撓度w)僅為x和y的函數(shù)。由幾何方程可得板內(nèi)應(yīng)變張量為

(3)

由式(3)可見(jiàn)，法向應(yīng)變?chǔ)舲z=0，此為板理論中的基本假設(shè)。將各應(yīng)變分量采用如下矢量形式表示為

(4)

1.1.1 橫觀各向同性板本構(gòu)關(guān)系

對(duì)于橫觀各向同性材料，當(dāng)各向同性面為xy面(z軸為旋轉(zhuǎn)對(duì)稱軸)時(shí)，其本構(gòu)關(guān)系[9]表示為

(5)

通常，由于板的幾何特征，法向應(yīng)力與其他應(yīng)力分量相比為可忽略的極小量σzz≈0，這也是板理論中常用的基本假設(shè)，將εzz=σzz=0代入式(5)得

(6)

故對(duì)于橫觀各向同性板式構(gòu)件，當(dāng)板平面xy為各向同性面(厚度為垂直于該面的方向z)時(shí)，其本構(gòu)方程由式(6)給出，以矩陣形式表示為

(7)

式(7)中的本構(gòu)矩陣記為C。類比式(4)中對(duì)應(yīng)變的拆分方式，將應(yīng)力及本構(gòu)矩陣分為如下兩部分。

(8)

板平面外應(yīng)力-應(yīng)變關(guān)系τ=C2γ，即

(9)

1.1.2 板內(nèi)應(yīng)變能及廣義內(nèi)力

節(jié)點(diǎn)位移在板中引起的應(yīng)變能ED表示為

(10)

式(10)中：Ω為整個(gè)積分區(qū)域；S為板中面面積。

(11)

(12)

(13)

(14)

圖3～圖5描述了板橫截面上的應(yīng)力，這些應(yīng)力與板平面內(nèi)單位長(zhǎng)度的力和力矩相聯(lián)系，即廣義內(nèi)力。其中薄膜應(yīng)力對(duì)應(yīng)于式 (15)所示廣義拉伸-壓縮(Nxx,Nyy)及板平面內(nèi)剪切(Nxy)力(圖3)，表達(dá)式為

圖3 廣義拉伸-壓縮及板平面內(nèi)剪切力

(15)

廣義橫向剪力Q定義為橫向剪切應(yīng)力在板厚度方向的積分(圖4)，表達(dá)式為

圖4 廣義橫向剪力

(16)

彎曲及扭轉(zhuǎn)應(yīng)力與沿板邊界上的廣義彎矩(Mxx和Myy)及扭矩(Mxy)相聯(lián)系(圖5)，表達(dá)式為

圖5 廣義彎(扭)矩

(17)

在x、y方向上，板的力矩平衡方程[10]為

(18)

1.1.3 橫向剪切的影響

Kirchhoff薄板理論類比于經(jīng)典梁理論(歐拉-伯努利梁理論)，忽略了橫向剪切變形的影響，假設(shè)橫向剪切應(yīng)變?chǔ)脁z及γyz為0，即

(19)

式(19)表征了薄板中撓度w與轉(zhuǎn)角矢量θ間的運(yùn)動(dòng)學(xué)關(guān)系：初始狀態(tài)下垂直于板中面的法線在變形過(guò)程中(及變形后)始終垂直于中面。Kirchhoff模型主要適用于沿厚度方向分布均勻的薄板(h/L≤1/10，L代表板的長(zhǎng)度及寬度)。

Mindlin-Reissner中厚板理論類比于鐵木辛柯梁理論，考慮了橫向剪切應(yīng)變?chǔ)脁z及γyz，并與廣義橫向剪力Q相聯(lián)系[式(16)]。如同鐵木辛柯梁的情況，考慮到實(shí)際的剪切應(yīng)變沿板厚度方向并非均勻分布，基于三維彈性理論剪切應(yīng)變能等效原則，引入校正系數(shù)k=5/6代入式(16)，則Mindlin-Reissner中厚板內(nèi)，廣義橫向剪力與橫向剪切應(yīng)變的關(guān)系定義為

(20)

中厚板在變形過(guò)程中，初始狀態(tài)下垂直于板中面的法線不再要求始終垂直于中面。Mindlin-Reissner模型適合于當(dāng)板的組成成分為不均勻、各向異性材料，及層合板的建模。事實(shí)上，在這些類型板結(jié)構(gòu)中橫向剪切作用占據(jù)重要因素，不可忽略。

1.2 DKT,DKQ,DST,DSQ板有限單元編程

基于平板彎曲問(wèn)題的特殊性，自有限元方法發(fā)展伊始，大量工作投入到了構(gòu)造板(及殼)單元的研究之中[11]。近60年來(lái)，板殼有限元分析一直是研究的熱點(diǎn)，有關(guān)板殼有限元的研究文獻(xiàn)已數(shù)以千計(jì)，文獻(xiàn)[12]引用了約150個(gè)板的有限元列示。僅對(duì)基于離散Kirchhoff理論構(gòu)造的三角形單元(DKT)和四邊形單元(DKQ，適用于薄板)及包含橫向剪切作用(無(wú)剪切鎖閉)的三角形單元(DST)和四邊形單元(DSQ，適用于中厚板)的構(gòu)造過(guò)程做清晰詳細(xì)的介紹與梳理。這些單元間的共同點(diǎn)在于基于單元應(yīng)變能構(gòu)造單元?jiǎng)偠染仃嚕?/p>

(21)

參考式 (11)～式 (14)中對(duì)整個(gè)板內(nèi)應(yīng)變能的定義如下。

1.2.1 單元位移場(chǎng)插值

若對(duì)位移場(chǎng)各分量進(jìn)行經(jīng)典離散，采用等參單元分別獨(dú)立插值，即

(22)

將導(dǎo)致剪切鎖閉現(xiàn)象，即當(dāng)板厚趨于零時(shí)，中厚板理論并沒(méi)有退化為薄板理論，剪切變形沒(méi)有趨于零。這是因?yàn)楫?dāng)板較厚時(shí)，擾度w及轉(zhuǎn)角βx、βy為獨(dú)立變量，而當(dāng)板非常薄時(shí)，βx、βy為w的導(dǎo)數(shù)[見(jiàn)式(19)],而非獨(dú)立變量。

板單元DKT、DKQ、DST、DSQ對(duì)位移場(chǎng)各分量采用了如下的插值函數(shù)[3-5,13]。

(23)

式(23)中：n為單元節(jié)點(diǎn)數(shù)，對(duì)DKT、DST 單元，n=3，對(duì)DKQ、DSQ單元，n=4。如圖6所示，以三角形單元為例，n、s分別為垂直及沿邊ij的單位向量，對(duì)ij邊上的任意一點(diǎn)k分別定義切向轉(zhuǎn)角βs及法向轉(zhuǎn)角βn為

圖6 切向轉(zhuǎn)角βs及法向轉(zhuǎn)角βn

(24)

式(24)中：Ck=(xj-xi)/Lk；Sk=(yj-yi)/Lk，

表1 單元DKT、DST、DKQ、DSQ的形函數(shù)

圖7 基準(zhǔn)單元節(jié)點(diǎn)及邊編號(hào)

在各邊界上，切向轉(zhuǎn)角βs二次變化，法向轉(zhuǎn)角βn線性變化(圖8)，它們由角節(jié)點(diǎn)上的參數(shù)完全確定，表達(dá)式為

圖8 轉(zhuǎn)角沿坐標(biāo)在邊上的變化

(25)

式(25)中：s′=s/Lk∈[0,1]；αk為變量，與切向轉(zhuǎn)角βs相關(guān)聯(lián)。

物理坐標(biāo)系(x,y)與基準(zhǔn)坐標(biāo)系(ξ,η)之間的等參變換公式為

(26)

并采用表1中的插值函數(shù)Ni(ξ,η)。兩種坐標(biāo)系間偏導(dǎo)數(shù)映射關(guān)系由雅可比矩陣J相聯(lián)系，即

(27)

式(27)中：J中各元素Jij表達(dá)式見(jiàn)表2，其逆矩陣記為j=J-1。

表2 雅可比矩陣J中各元素Jij表達(dá)式

1.2.2 單元應(yīng)變場(chǎng)插值

單元薄膜應(yīng)變場(chǎng)分量表示如下。

(28)

以矩陣形式表示為

(29)

式(29)中：Bm為薄膜應(yīng)變幾何函數(shù)矩陣；Um為板平面內(nèi)位移場(chǎng)矢量；Bm及Um定義如下。

(30)

單元曲率(及扭率)場(chǎng)χ和橫向剪切應(yīng)變場(chǎng)γ的插值過(guò)程相對(duì)單元薄膜應(yīng)變場(chǎng)e復(fù)雜。對(duì)于DKT和DKQ單元，變量αk可以通過(guò)橫向剪切應(yīng)變?yōu)?(Kirchhoff薄板假設(shè))導(dǎo)出，即

(31)

將式(24)代入式(31)積分得

Ckβxj+Skβyj)

(32)

轉(zhuǎn)角βx、βy的插值函數(shù)由式(23)給出，可得

(33)

式(33)中：

(34)

式(34)中：Uf為撓度轉(zhuǎn)角矢量；指標(biāo)k、m被定義為以節(jié)點(diǎn)頂點(diǎn)i為公共點(diǎn)的兩邊(見(jiàn)圖7)，其編號(hào)取值見(jiàn)表3；插值函數(shù)Ni、Pk表達(dá)式見(jiàn)表1。

表3 DKT, DKQ單元節(jié)點(diǎn)及邊編號(hào)i、k、m

DKT、DKQ單元曲率(及扭率)場(chǎng)χ為

(35)

(36)

對(duì)于DST及DSQ單元，由于需要考慮橫向剪切應(yīng)變，式(31)～式(32)不再適用。DST、DSQ單元曲率(及扭率)場(chǎng)χ為

χ=BfβUf+Bfαα

(37)

式(37)中：

(38)

且單元橫向剪切應(yīng)變能為

(39)

(40)

式(40)中：

(41)

Cfij(i,j=1,…,3)為矩陣Cf[式(13)]中的元素，βx及βy采用式(23)所示的方式插值得

βxx=PfUf+T2Tαα

(42)

式(42)中：

(43)

(44)

(45)

聯(lián)立式(40)及式(42)可得

(46)

(47)

類比式 (31)，式(47)積分為

(48)

式(48)以矩陣形式表示為

(49)

式(49)中：Aα、Aw表達(dá)式如式(50)、式(51)所示。

(52)

(50)

(51)

(53)

1.2.3 單元?jiǎng)偠染仃?/p>

(54)

(55)

對(duì)于DST、DSQ單元，考慮了橫向剪切的影響，故單元應(yīng)變能eD為

(56)

其中單元薄膜剛度矩陣Km見(jiàn)式(55)，且

(57)

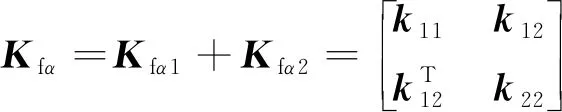
(58)

并將式(49)與式(58)代入式(56)，得DST、DSQ單元應(yīng)變能eD為

(59)

式(59)中：

(60)

根據(jù)式(54)與式(59)，對(duì)于DKT、DKQ、DST、DSQ板單元，單元應(yīng)變能eD統(tǒng)一表示為

(61)

式(61)中：U2d=[u1v1w1βx1βy1…unvnwnβxnβyn]T為單元節(jié)點(diǎn)位移矢量，每個(gè)節(jié)點(diǎn)5個(gè)自由度；K2d為板單元?jiǎng)偠染仃嚒?/p>

2 層合板結(jié)構(gòu)靜力試驗(yàn)及數(shù)值分析

2.1 橫觀各向同性板結(jié)構(gòu)靜力試驗(yàn)

如圖9所示，試驗(yàn)樣品為由刨花板組裝而成的辦公桌。試驗(yàn)開(kāi)始之前將各板擰緊拼裝，并儲(chǔ)存在相對(duì)濕度50%±5%及室溫(23±2) ℃的環(huán)境中。試驗(yàn)在溫度范圍介于15～25 ℃的環(huán)境條件下進(jìn)行。試驗(yàn)荷載通過(guò)負(fù)載墊施加于桌面中心，負(fù)載墊對(duì)應(yīng)于圖9的直徑為80 mm，具有光滑、平坦接觸表面的剛性圓柱體。在所施加荷載點(diǎn)的對(duì)立面設(shè)置LVDT位移傳感器并與書桌下表面相接觸，以測(cè)量相對(duì)應(yīng)的荷載點(diǎn)處的位移值。測(cè)試過(guò)程中，分批次分別施加3級(jí)荷載F為300、400、500 N，每次均緩慢施加力以忽略動(dòng)態(tài)影響，且每次所施加的靜態(tài)力均保持10 s以記錄實(shí)驗(yàn)數(shù)據(jù)(力和位移)。為了減少試驗(yàn)測(cè)量的不確定性因素，每級(jí)荷載施加10次，并計(jì)算得出測(cè)量的平均值以代表該級(jí)荷載-位移的試驗(yàn)結(jié)果。板中心擾度定義為在沒(méi)有施加力時(shí)的初始狀態(tài)和施加荷載后的最終狀態(tài)之間位移計(jì)讀書的差值。每級(jí)荷載下位移計(jì)的初始及最終讀數(shù)統(tǒng)計(jì)于表4。

圖9 垂直靜力荷載試驗(yàn)

表4 每級(jí)荷載作用下位移計(jì)初始及最終讀數(shù)

2.2 DKT,DKQ,DST,DSQ板單元驗(yàn)證及性能比較

關(guān)于厚薄板彎曲問(wèn)題的理論解，有大量文獻(xiàn)涵蓋了基于Kirchhoff薄板及Mindlin-Reissner中厚板理論的矩形及圓形板在不同荷載及邊界條件下的理論解[14-15]。其中，對(duì)于邊界簡(jiǎn)支或固定的矩形板，其理論解通常采用級(jí)數(shù)法或伽遼金方法的近似解法，而無(wú)精確解。比較了圓板分別在中心點(diǎn)荷載及板平面均布荷載作用下、邊界簡(jiǎn)支及固定時(shí)，圓心撓度的理論精確解與有限元數(shù)值解，從而驗(yàn)證前述4種板單元的性能。

如圖10所示的圓板，其直徑為R，厚度h?R，由均質(zhì)各向同性線彈性材料制成，其彈性模量為E，剪切模量為G，泊松比為ν，抗彎剛度D=Eh3/[12(1-ν2)]。

圖10 圓板受均布荷載

此為軸對(duì)稱問(wèn)題，以圓心為原點(diǎn)，建立圓柱坐標(biāo)系(er,eθ,ez)，板內(nèi)某點(diǎn)的橫向位移(撓度)w(r)及轉(zhuǎn)角θθ(r)均僅為徑向距離r的函數(shù)。對(duì)于物理量s(s表示撓度w或轉(zhuǎn)角θθ)，定義s的理論解sana與有限元數(shù)值解snum之間的相對(duì)誤差函數(shù)Errors為

(62)

式(62)中：=·=為L(zhǎng)2范數(shù)。

當(dāng)荷載及邊界條件不同時(shí)，基于兩種板理論求得的撓度及轉(zhuǎn)角的理論解分別歸納如下。

(1)板邊界固定、板面受均布荷載p。

(63)

(2)板邊界簡(jiǎn)支、板面受均布荷載p。

(64)

(3)板邊界固定、中心受集中荷載P。

(65)

(4)板邊界簡(jiǎn)支、中心受集中荷載P。

(66)

DKT、DKQ、DST、DSQ板單元性能的評(píng)估可通過(guò)計(jì)算板在不同邊界條件下，撓度及轉(zhuǎn)角的解析解和有限元數(shù)值解間的相對(duì)誤差而實(shí)現(xiàn)。圖11～圖14展示了圓形板分別在邊界固定、簡(jiǎn)支、板面受均布荷載、圓心受集中荷載作用時(shí)，對(duì)應(yīng)不同的板單元，在除圓心以外所有節(jié)點(diǎn)的相對(duì)誤差[式(62)]隨板單元數(shù)量的變化規(guī)律。各個(gè)板單元的有限元數(shù)值解通過(guò)MATLAB軟件計(jì)算。

圖11 撓度及轉(zhuǎn)角相對(duì)誤差隨單元數(shù)量的演變(板邊固定、板面受均布荷載)

圖12 撓度及轉(zhuǎn)角相對(duì)誤差隨單元數(shù)量的演變(板邊簡(jiǎn)支、板面受均布荷載)

圖13 撓度及轉(zhuǎn)角相對(duì)誤差隨單元數(shù)量的演變(板邊固定、中心受集中荷載)

圖14 撓度及轉(zhuǎn)角相對(duì)誤差隨單元數(shù)量的演變(板邊簡(jiǎn)支、中心受集中荷載)

2.3 板在空間內(nèi)的組裝與坐標(biāo)變換

圖9所示的辦公桌為板式構(gòu)件組成的空間結(jié)構(gòu)。如圖15所示，以三節(jié)點(diǎn)三角形單元為例，解釋說(shuō)明板在空間的組裝。該三角形單元位于由全局(或空間)坐標(biāo)系(X,Y,Z)組成的空間體系中。對(duì)于每個(gè)單元定義局部坐標(biāo)系(x,y,z)。

圖15 空間內(nèi)三節(jié)點(diǎn)三角形板單元

則矢量y定義為：y=z×x。

在全局坐標(biāo)系(X,Y,Z)及局部坐標(biāo)系(x,y,z)中，節(jié)點(diǎn)i的位移ui及轉(zhuǎn)角Ωi分別定義如下。

(67)

可得單元節(jié)點(diǎn)上5個(gè)自由度表示為

(68)

引入矩陣T，式(68)以矩陣形式表示為

(69)

式(69)中：大小為5n×6n矩陣T對(duì)應(yīng)于位移場(chǎng)從全局坐標(biāo)系到局部坐標(biāo)系的轉(zhuǎn)換矩陣，式(61)中單元應(yīng)變能為

(70)

式(70)中：K2d為板平面內(nèi)單元?jiǎng)偠染仃嚒Ｔ诳臻g內(nèi)，單元?jiǎng)偠染仃嚩x為

K3d=TTK2dT

(71)

同理，2.1節(jié)中介紹的代表材料彈性特征的本構(gòu)關(guān)系也必須由局部坐標(biāo)系轉(zhuǎn)換為在空間的全局坐標(biāo)系中表示，以實(shí)現(xiàn)單元?jiǎng)偠染仃嚨慕M裝。為此，定義局部坐標(biāo)系(x,y,z)與空間坐標(biāo)系(X,Y,Z)間的過(guò)渡矩陣P為

(72)

矩陣P為正交矩陣(P-1=PT)，P的列分別對(duì)應(yīng)于矢量X、Y、Z的坐標(biāo)在局部坐標(biāo)系(x,y,z)中的表達(dá)式。

應(yīng)力及應(yīng)變張量分量在全局坐標(biāo)系(X,Y,Z)中分別表示為σ′ij及ε′ij，與其局部坐標(biāo)系中分量σij及εij間的轉(zhuǎn)換定律為

(73)

式(73)中：下標(biāo)i,j,k,l=1,2,3。

廣義胡克定律在局部坐標(biāo)系(x,y,z)中表示為

(74)

式(74)中：Cijkl及Sijkl分別為四階剛度張量C及柔度張量S在局部坐標(biāo)系中分量。將式(74)所示的廣義胡克定律在全局坐標(biāo)系(X,Y,Z)中表示，可得Cijkl與四階剛度張量C′在全局坐標(biāo)系(X,Y,Z)中分量C′ijkl之間的轉(zhuǎn)換關(guān)系為

(75)

式(75)中：下標(biāo)i,j,k,l=1,2,3;p,q,r,s=1,2,3。

對(duì)四階柔度張量S及S′在局部坐標(biāo)系與全局坐標(biāo)系中的分量Sijkl與S′ijkl間的轉(zhuǎn)換關(guān)系可采用與式(75)相似的方式。

利用Voigt標(biāo)記，對(duì)下標(biāo)設(shè)置如下轉(zhuǎn)換規(guī)則，即

11?1, 22?2, 33?3, 23或32?4， 13或31?5， 12或21?6

(76)

可將應(yīng)力、應(yīng)變張量表示成向量形式為

(77)

及將四階剛度張量C(或C′)及柔度張量S(或S′)表示成6×6矩陣C(或C′)及S(或S′)為

(78)

可得矢量形式的應(yīng)力、應(yīng)變及二階6×6矩陣形式的剛度張量及柔度張量分別在局部坐標(biāo)系與全局坐標(biāo)系中的轉(zhuǎn)換關(guān)系如下。

(79)

式(79)中：Mσ及Mε為大小6×6的可逆矩陣，具有如下形式。

(80)

式(80)中：子矩陣A、B、D1、D2為

(81)

易得矩陣Mσ與Mε間聯(lián)系為

(82)

矩陣Mσ與Mε不同的主要原因在于式(77)中定義應(yīng)力、應(yīng)變矢量時(shí)，切應(yīng)變分量中系數(shù)2的存在，而切應(yīng)力分量沒(méi)有。

2.4 有限元數(shù)值分析

圖16展示了通過(guò)MATLAB軟件，將各個(gè)板構(gòu)件組裝成圖9所示的試驗(yàn)辦公桌模型，實(shí)際的三維板式構(gòu)件由板中面表示。

各板編號(hào)1、2、3的尺寸見(jiàn)表5。在辦公桌中心處通過(guò)直徑D=80 mm的圓柱形負(fù)載墊施加的集中力荷載F，由板中心直徑為D的圓上均布荷載p=4F/(πD2)表示。不考慮書桌與地面間的相對(duì)滑動(dòng)(事實(shí)上試驗(yàn)過(guò)程中也未見(jiàn))，故在桌腳處采用固定的邊界條件。

表5 板構(gòu)件尺寸

刨花板材料的力學(xué)性能由“橫觀各向同性”本構(gòu)關(guān)系模擬。由式(7)可見(jiàn)，影響橫觀各向同性板式構(gòu)件的材料參數(shù)僅有3個(gè)：橫向彈性模量ET，橫向泊松比νT及縱向剪切模量GL。對(duì)刨花板材料參數(shù)的測(cè)量[8-9]并非重點(diǎn)內(nèi)容。事先采用文獻(xiàn)[16]方法對(duì)刨花板各項(xiàng)力學(xué)參數(shù)進(jìn)行了試驗(yàn)測(cè)量，結(jié)果統(tǒng)計(jì)見(jiàn)表6。

表6 刨花板材料參數(shù)測(cè)量結(jié)果平均值

分別應(yīng)用Kirchhoff薄板單元(DKT、DKQ單元)及Mindlin-Reissner中厚板單元(DST單元)代入有限元模型計(jì)算桌面中心點(diǎn)處撓度，并與3.1節(jié)中試驗(yàn)測(cè)量值相比較，結(jié)果見(jiàn)表7。圖16對(duì)應(yīng)于施加中心集中荷載F=300 N、并采用DKT單元計(jì)算時(shí)，在全局坐標(biāo)系下豎向位移云圖。由表7統(tǒng)計(jì)結(jié)果可見(jiàn)，薄板與中厚板有限元單元計(jì)算結(jié)果均能滿足工程計(jì)算精度，但對(duì)于計(jì)算刨花板這種夾層材料復(fù)合板，考慮剪切作用的中厚板單元比薄板單元計(jì)算更加精確。

圖16 板結(jié)構(gòu)靜力試驗(yàn)?zāi)M

表7 試驗(yàn)測(cè)量值與有限元數(shù)值解比較

3 結(jié)論

隨著有限元方法的發(fā)展，對(duì)板(及殼)有限元的研究，如何構(gòu)造出經(jīng)濟(jì)、高效、厚薄板通用的板有限單元，一直吸引著眾多科研工作者的目光。以刨花板材料板式結(jié)構(gòu)辦公桌家具為例，對(duì)其進(jìn)行了靜力荷載試驗(yàn)及有限元數(shù)值分析，并進(jìn)行了結(jié)果對(duì)比，得到主要結(jié)論及展望如下。

以刨花板代表的層合板，因其特殊的物理構(gòu)造，在各向同性平面內(nèi)材料的力學(xué)性質(zhì)大致相同，而垂直于此方向不同，故可以采用橫觀各向同性本構(gòu)關(guān)系對(duì)其建模。影響橫觀各向同性材料的彈性參數(shù)有5個(gè)：縱向、橫向彈性模量EL、ET，縱向、橫向泊松比νL、νT及縱向剪切模量GL。板式構(gòu)件由于在厚度方向尺寸遠(yuǎn)小于其他兩個(gè)方向，其法向正應(yīng)力通常被忽略不計(jì)。將這一假設(shè)代入橫觀各向同性材料本構(gòu)方程，得到了橫觀各向同性板式構(gòu)件的本構(gòu)關(guān)系。影響橫觀各向同性板的力學(xué)參數(shù)僅有3個(gè)：ET、νT及GL。

基于薄板及中厚板理論中對(duì)橫向剪切不同的假設(shè)，對(duì)DKT、DKQ薄板單元及DST、DSQ中厚板單元的構(gòu)造方法進(jìn)行了詳細(xì)的梳理與介紹。通過(guò)對(duì)比圓板彎曲問(wèn)題中理論解的精確值與有限元數(shù)值解的相對(duì)誤差，對(duì)各個(gè)板單元的性能進(jìn)行了驗(yàn)證。結(jié)果表明，DKT、DKQ及DST單元是足夠精確可靠的，造成DSQ單元數(shù)值解不收斂于理論解的主要原因，分析認(rèn)為主要在于對(duì)橫向剪力插值的幾何函數(shù)矩陣中，高斯近似積分法的應(yīng)用。同時(shí)介紹了板構(gòu)件在空間內(nèi)的組裝及材料參數(shù)、節(jié)點(diǎn)自由度分量向空間全局坐標(biāo)系的轉(zhuǎn)換方法。

將刨花板材料參數(shù)的測(cè)量平均值及DKT、DKQ、DST單元分別代入有限元模型進(jìn)行計(jì)算，并與板結(jié)構(gòu)靜力試驗(yàn)結(jié)果對(duì)比，可見(jiàn)上述板單元均能滿足工程精度，而考慮橫向剪切作用的DST中厚板單元對(duì)層合板的計(jì)算結(jié)果更加精確。僅從不同的板單元及材料參數(shù)的平均值，對(duì)有限元模型進(jìn)行了計(jì)算，其結(jié)果具有一定的偶然性。事實(shí)上，影響該有限元模型的因素除此之外主要還有刨花板材料參數(shù)的離散性，及各板式構(gòu)件之間的連接剛度等。

為此，展望如下：①構(gòu)造刨花板材料參數(shù)隨機(jī)概率模型；②試驗(yàn)測(cè)量板式構(gòu)件之間連接件的實(shí)際剛度，并代入有限元模型計(jì)算。