陶 翔，陳玲紅，蔣旭光，吳學成，岑可法

（浙江大學 能源清潔利用國家重點實驗室，浙江 杭州 310027）

0 引 言

入爐煤特性對電廠鍋爐安全經濟環保運行有著十分重要的意義[1]，能否實時獲取入爐煤質參數是指導鍋爐運行的關鍵。 由于煤質在線分析設備成本投入較高的原因，目前電廠普遍未能實現入爐煤實時在線檢測[2，3]，大都采用離線采樣化驗的方式獲取入爐煤參數，該方法存在時間嚴重滯后的問題。 近十幾年，基于數據建模和機器學習的在線煤質軟測量技術得到廣泛研究和應用[2，3]。

電廠燃用煤種多樣化，需要摻配不同煤種成為電廠普遍面臨的問題，而入爐煤質受到動力配煤的影響。 我國開展了大量關于配煤摻燒的理論和試驗研究，包括混煤參數計算、配煤優化和專家系統開發等[4-6]。 針對單煤和混煤的煤質特性、燃燒特性和污染物排放特性，通過試驗研究，給出了混煤的各指標參數與組成單煤之間具有復雜的非線性關系的這一結論，而采用神經網絡等機器學習方法可以獲得比線性模型更準確的結果[7-9]。

浙江大學熱能工程研究所是我國較早進行配煤研究的單位，提出了完整的動力配煤模型[10-12]。該模型需要一定的混煤摻燒試驗數據和鍋爐運行數據作為支撐，實際應用中可根據需求考慮約束條件。 配煤目標根據實際情況可分為三種：追求成本最低、追求優質煤種配比最小、追求劣質煤種配比最大[13]。 配煤優化算法方面主要包括神經網絡[14，15]、遺傳算法[16，17]、模擬退火算法、粒子群算法、布谷鳥算法[18]等。

某電站煤場共八個區域用于存放不同礦點煤質，擔負向6 臺鍋爐機組供煤的生產任務。 6 臺鍋爐分三期建設，整體的燃燒性能存在較大不同，煤場配煤應滿足鍋爐對燃煤煤質特性的不同需求，特別是針對運行時間長、容易結焦、爐膛污染物排放嚴重的鍋爐，需要摻配出準確的混煤以滿足正常生產需要。

煤場配煤依據人工經驗，將高硫煤與低硫煤、高熱值煤與低熱值煤簡單進行摻混，考慮單一指標，沒有準確的摻配指導，缺乏理論依據和數據支撐，容易造成混煤煤質不符合鍋爐燃燒的需求。

此外，電廠入爐煤經采樣化驗到公布結果，存在較長的時間滯后，待公布化驗結果，該煤早已入爐燃燒完畢，無法有效指導鍋爐燃燒。

本文基于構建適用于鍋爐運行實際的配煤摻燒模型和混煤煤質計算方法，系統溯源來煤入廠至入爐燃燒的全環節信息數據，快速計算獲取入爐煤煤質參數。

1 分析方法

1.1 聚類分析方法

聚類分析依據對象的相似性對其進行分類，是一種無監督式學習的算法。 k均值聚類（kmeans clustering）算法是典型的基于距離劃分的聚類分析方法。 聚類的目標是將數據集按照同簇數據距離盡可能小、不同簇數據距離盡可能大的原則進行劃分。 假設簇劃分為（C1，C2，…，Ck），則算法目標是最小化誤差E：

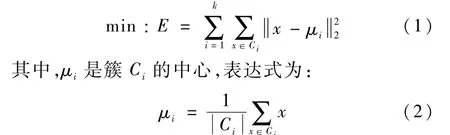
k-均值聚類算法具體過程如下：

（1）確定需要劃分的簇數k值，采用k-means算法確定k個初始聚類中心點；

（2）計算所有數據點到各個中心點的距離；

（3）將每個數據點分配到距離最近的中心點所屬的類別；

（4）計算每類數據點的平均值以獲得k個新的中心點位置；

（5）重復步驟（2）到（4），直到聚類中心點不再發生改變。

1.2 配煤摻燒計算模型

1.2.1 混煤煤質計算

配煤模型研究的核心是對混煤煤質的確定，對于混煤煤質指標是否具備可加性存在較大爭議。 陳文敏等[19]研究動力配煤主要煤質指標可加性，指出揮發分、發熱量、硫分等煤質指標具有可加性，而由于水分經常變動，認為混煤水分不宜用可加性計算。 此外，陳懷珍[20]指出組成混煤的單煤配比必須明確是在什么基準下的配比，因為只有單煤煤質指標和配煤量比例都處于同一基準下，才能使用常規的加權平均法。 可見，即便煤質參數指標具備可加性，仍然需要在理論計算值的基礎上進行修正。

若煤場兩路供煤，從兩個供煤區域取兩種不同的單煤，編號i為1、2。 兩種煤的煤量為B1和B2，假定兩種煤充分混合，以單煤的空氣干燥基為基準進行配煤。

由于煤量B1、B2是以空干基為基準的配比，因此可以直接使用煤量加權平均值計算混煤的空干基成分，如式（3）所示。

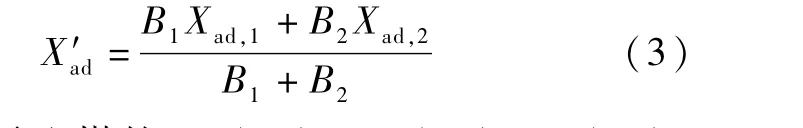
式中，X′ad表示配煤的Sad（%）、Mad（%）、Aad（%）、Vad（%）、或Qnet.ad（MJ/kg）加權值；Xad，1、Xad，2表示甲、乙兩種單煤對應的空干基煤質參數；B1、B2表示甲、乙兩種煤的空干基配煤質量，t。

除了直接使用式（4），也可以先使用式（3） 計算出混煤的Vad、Mad和Aad值。而混煤同樣是一種煤，滿足煤的不同基準之間的換算公式，故有：

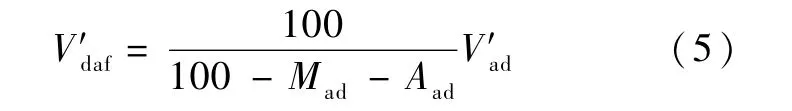
使用式（3） 和式（5） 計算的結果和式（4） 相同。

表1 列出了以空氣干燥水分基準配比時，其他基準配比的換算系數。

為判斷實際混煤煤質是否具備可加性，需對混煤的試驗值與加權值之間的誤差作出分析，可采用數理統計中的t檢驗法，判斷煤質指標參數計算值與實測值出現的誤差屬于試驗誤差還是顯著性差異。

以煤質實測值與加權值之間的差值作為樣本，構建樣本誤差矩陣：

樣本矩陣中m表示煤質指標個數，n 表示樣本數。

如果某煤質指標具有線性可加性，那么實測值與加權平均值之間的誤差服從正態分布ξ～N（μ，σ2），其中σ2未知，μ=0。 有，

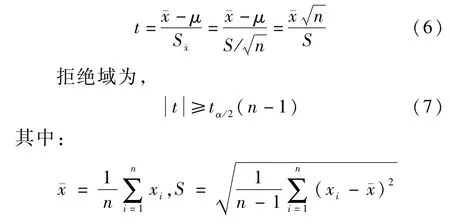
式中，ˉx為樣本均值；S 為樣本標準差；α為檢驗的顯著性水平。

1.2.2 配煤摻燒模型

混煤摻燒是通過將兩種或多種不同的單煤以一定的比例進行摻配，使摻配后的混煤特性達到鍋爐燃燒和污染物排放的要求。

依據鍋爐對具體煤質的要求和重要性排序，賦予不同權重，如表2 所示。

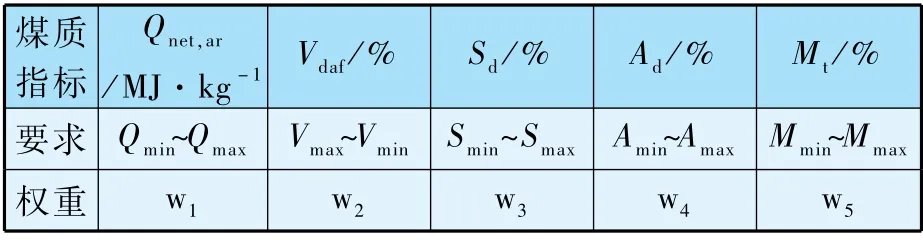
表2 煤質參數權重和要求范圍

依據各煤質參數的要求范圍，給出如下配煤摻燒模型：

上述計算模型可依據不同的配煤目標，輸出不同的摻配方案，包括混煤煤種和配比。

1.3 入爐煤質獲取計算模型

為提高入爐煤獲取的時效性，梳理從入廠來煤到入爐煤采樣的全環節和全數據流，圖1 示出了整個詳細過程。

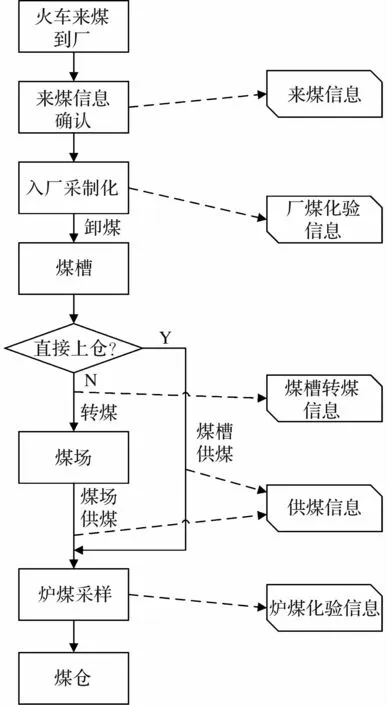
圖1 煤場火車來煤到供煤全環節和信息流

煤場是兩條皮帶雙路供煤，以表3 為例，說明供煤信息提供的數據內容。

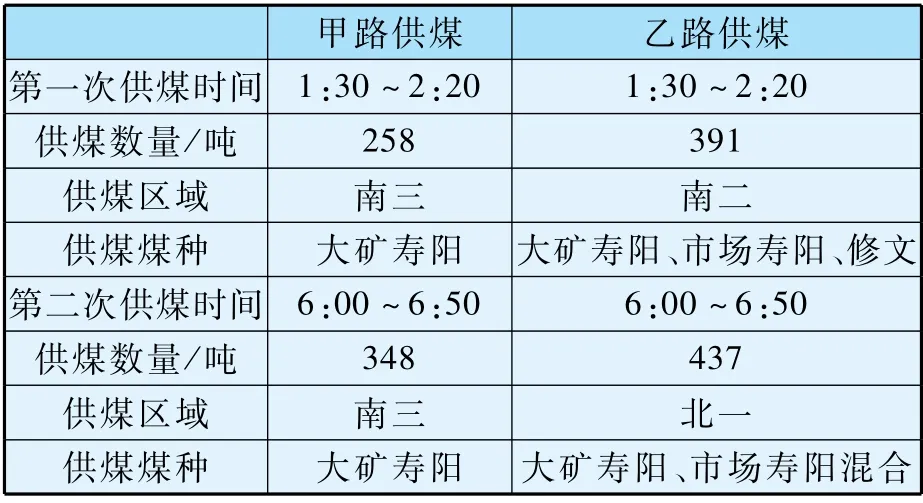
表3 班次供煤信息

為確定皮帶入爐煤參數，即供煤煤質參數，有如下思路：

依據供煤信息的供煤區域和供煤煤種，追溯從煤槽轉煤到煤場的該區域的該煤種數據，即確定了煤槽轉煤信息，依據煤槽轉煤時間和轉煤煤種，匹配更早的火車來煤信息。 即確定了某時刻供煤對應的火車來煤信息，進一步依據火車來煤信息查詢到入廠煤的化驗數據信息，最終確定供煤煤質信息，打通入廠煤化驗數據與入爐煤煤質之間的數據隔閡。

供煤信息溯源到入廠煤的化驗數據信息，整個流程為圖1 所示流程的逆向流程。 而電廠入爐煤的化驗數據可以用于驗證上述流程所得到的入爐煤參數。

上述思路的關鍵在于如何根據表3 的供煤信息去逆向推定煤場該區域的煤種何時從煤槽轉入的，然后再確定煤槽的煤是何批次火車來煤，進而去查找入廠煤化驗數據。 存在以下難點：

（1）由煤種名稱無法確定煤質準確信息，同樣名稱的煤種特性變化較大，根據轉煤煤種難以確定來煤批次；

（2）火車卸煤到煤槽，會與煤槽存煤發生混合；

（3）煤場情況混亂，整個煤場分區不夠精細。

針對上述難點，提出如下假設：

（1）從煤槽轉入煤場的煤可以在幾天內快速用完，即供煤區域的某個煤種即為上次從煤槽轉入到該區域的煤種，不包含更久之前的剩余煤；

（2）煤車來煤卸到煤槽，與煤槽存煤不發生混合，煤槽轉出的煤種和煤量按煤車來煤先后循序依次轉出。

2 分析與討論

2.1 入廠煤質聚類分析結果

電廠來煤存在多個煤種，煤質參數分布較廣，使用k均值聚類算法對入廠煤的低位發熱量Qnet，ar、揮發分Vdaf、硫分Sd、灰分Ad和全水分Mt進行聚類處理。 以低位發熱量為例，圖2 示出了其聚類分析的結果（k=4）。 從中可以看出煤質的集中分布情況及其典型數值。

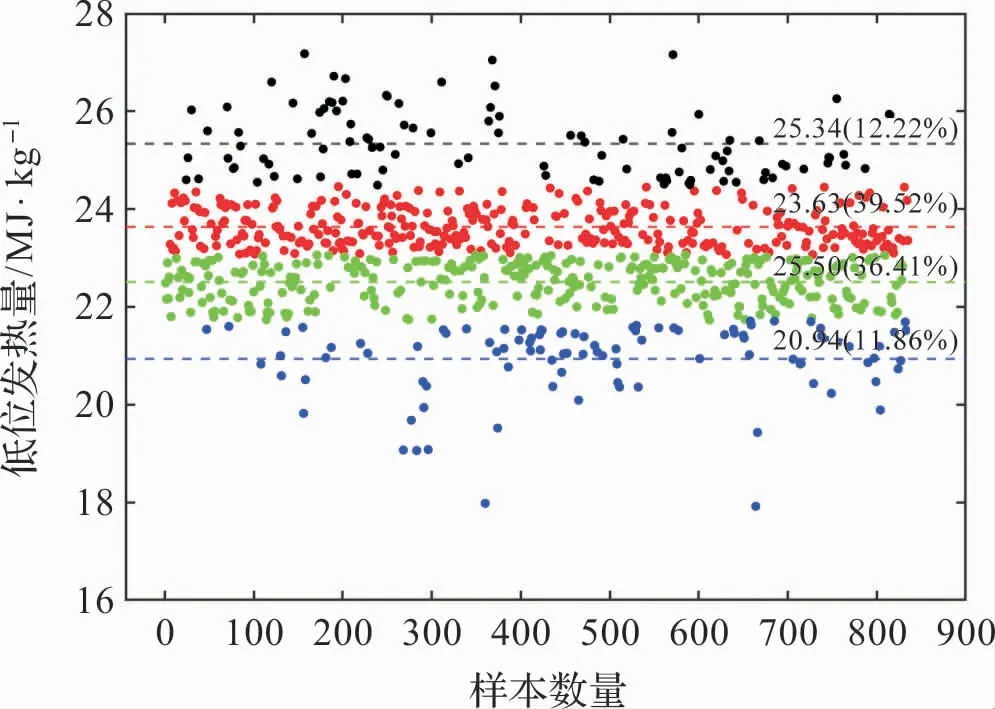
圖2 低位發熱量聚類分析結果

表4 是五個煤質指標聚類中心和占比情況，按占比大小來看，入廠煤發熱量Qnet，ar的典型數值為22.50 MJ/kg和23.63 MJ/kg；Vdaf的典型結果為14.47%和15.78%；Sd典型數值為0.36%和0.89%；Ad典型數值為25.54%和28.92%；Mt典型結果為5.27%、6.62%和8.11%。 入廠煤參數為配煤摻燒研究和入爐煤特性計算提供數據基礎。

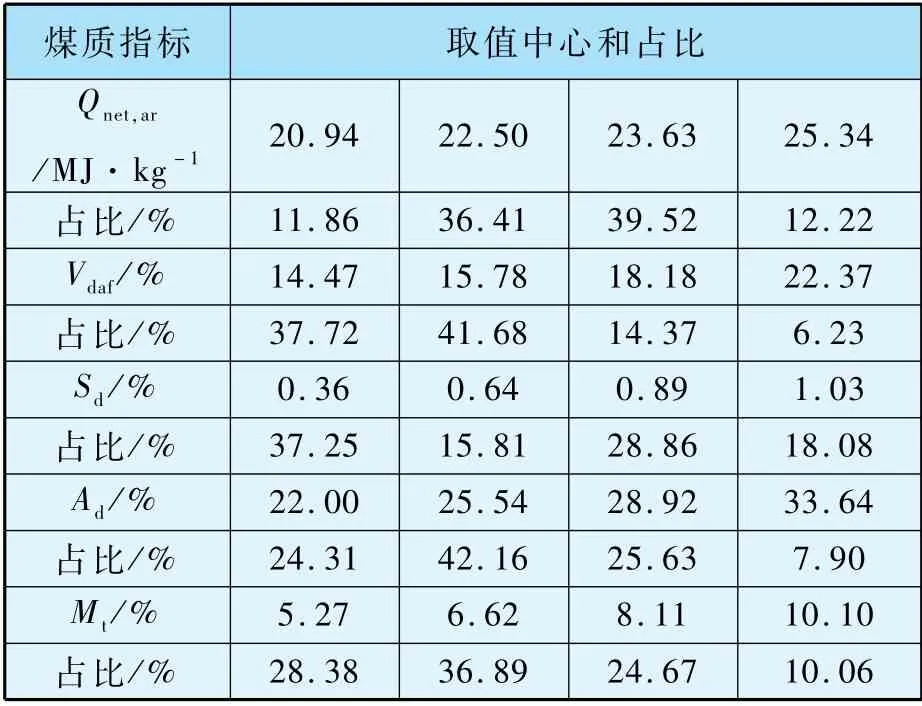
表4 入廠煤質聚類分析結果

2.2 混煤煤質確定方法

依據t檢驗方法，對30 組混煤的發熱量Qnet，ar、揮發分Vdaf、硫分Sad、灰分Aad和水分Mt的實測值和加權平均值進行比較，混煤煤質指標統計結果如表5 所示。

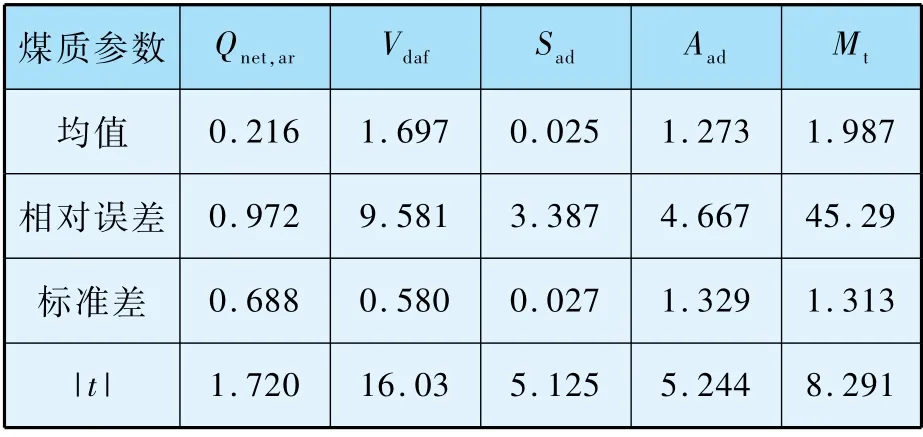
表5 煤質參數實測值和加權值偏差統計結果

查詢t分布表，有tα/2（30 -1） =2.045（α取0.05），發現只有Qnet，ar的|t|值小于該值，因此認為只有Qnet，ar具備可加性，而混煤的Vdaf、Sad、Aad和水分不具備可加性，水分相對誤差很大，這是由于水分經常變動，故混煤水分不宜用可加性計算。

對Vdaf、Sad和Aad進行線性擬合，將加權計算值作為自變量，實測值作為因變量，擬合結果如圖3 所示。

圖3（a）為揮發分Vdaf擬合結果，擬合公式如下：

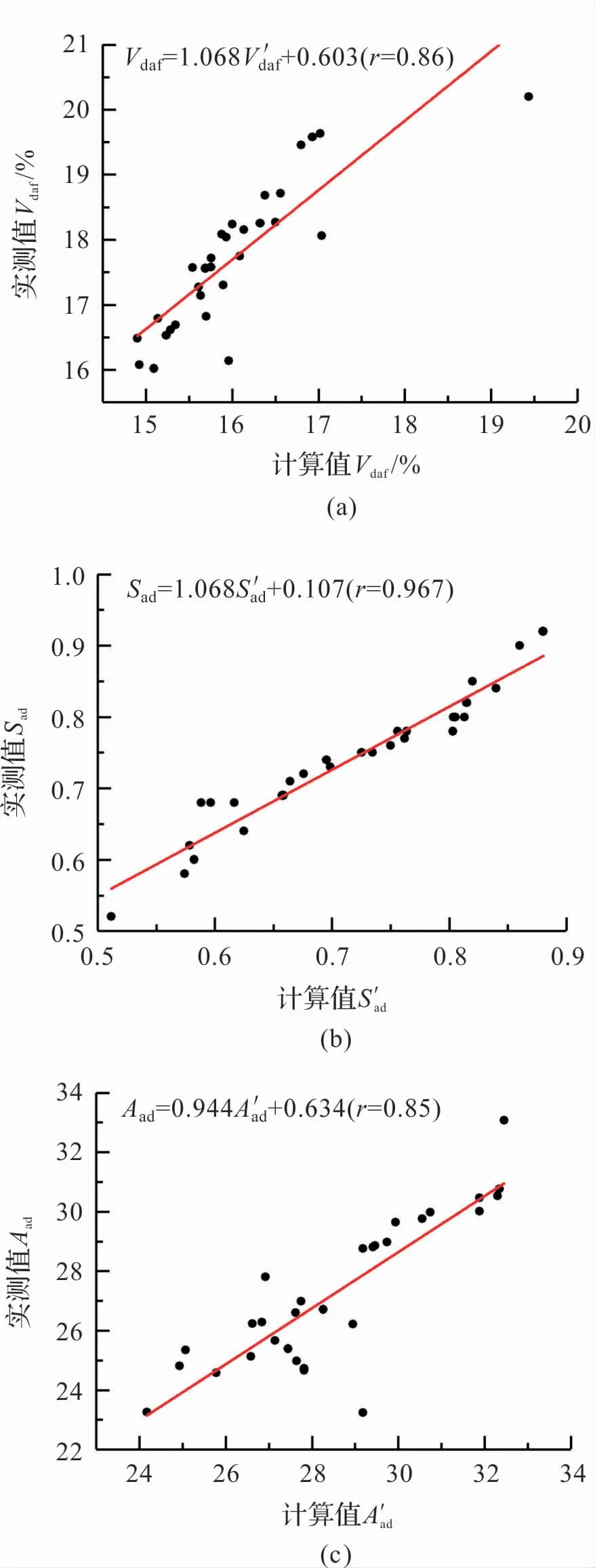
圖3 混煤V daf、S ad、A ad擬合結果

因此，本文在對混煤煤質的計算中，發熱量采用加權平均值，揮發分、硫分和灰分使用擬合公式，而水分不宜通過計算得到。

2.3 配煤模型輸出供煤方案

依據電廠鍋爐設計煤種和實際燃燒運行工況，并結合電站運行人員反饋的建議，整理出鍋爐燃燒對煤質參數重要性排序和要求范圍，如表6所示。

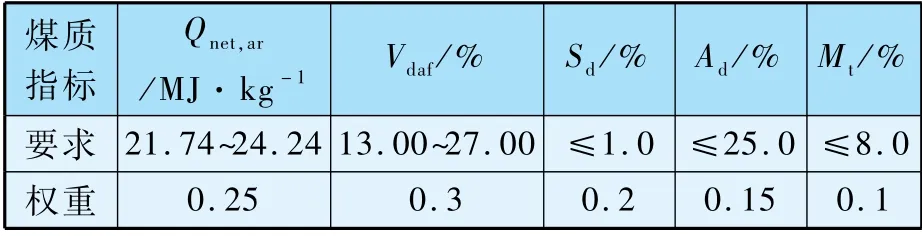
表6 煤質參數權重和要求范圍

依據混煤煤質計算方法和配煤模型，以2021年5 月5 日至2021 年5 月10 日期間轉入煤場的單煤為例，不同配煤目標輸出不同供煤方案，如下表所示。 表7 所示的摻配方案包括混煤煤種和對應配比，具有實際的可操作性。

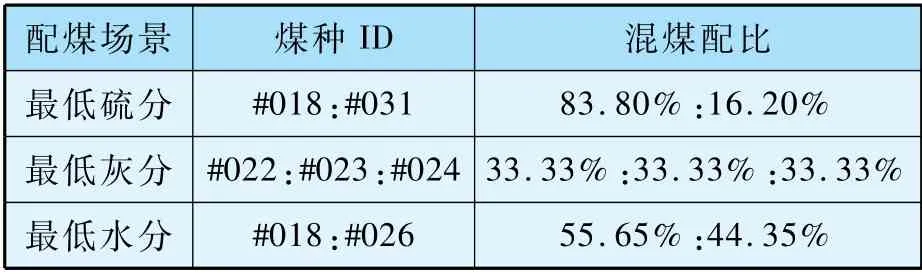
表7 不同配煤目標下的摻配方案

2.4 入爐煤歷史化驗數據分析結果

圖4 為入爐煤質歷史化驗數據，發熱量Qnet，ar主要集中在21 ～24 MJ/kg之間，普遍大于設計煤種21.69 MJ/kg，可能造成鍋爐運行調整困難，加大煙溫偏差；揮發分呈現大部分集中的特點，絕大部分揮發分在14% ～20%之間，滿足設計煤種15.64%的要求；而硫分分布較為分散，在0.5% ～1.0%之間都有相當的占比，不穩定，硫分較大波動容易造成SO2排放突然超標；灰分要求不大于25%，而幾乎存在一半位于25%以上，造成不完全燃燒損失較大，受熱面積灰結焦嚴重。

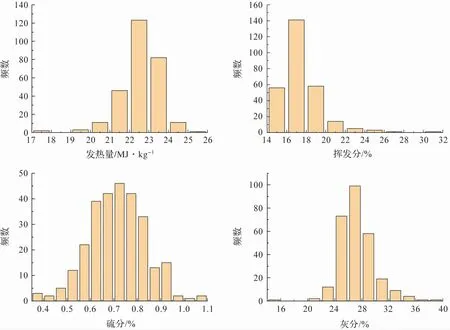
圖4 入爐煤發熱量、揮發分、硫分和灰分頻數分布圖

對入爐煤灰分Ad、高位發熱量Qgr，d、低位發熱量Qnet，ar的實測數據進行統計分析，以灰分Ad作為自變量，高位和低位發熱量作為兩個因變量，得到圖5（a）所示結果，回歸方程為式（11）和式（12）；以高位發熱量Qgr，d為自變量，低位發熱量Qnet，ar為因變量，得到圖5（b）所示結果，回歸方程為式（13）。

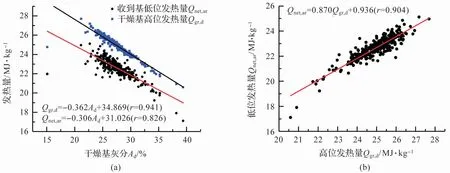
圖5 入爐煤發熱量和灰分的分析結果

從圖5（a）和式（12）可以看出收到基低位發熱量Qnet，ar和干燥基灰分Ad之間的線性擬合關系并不是很好，其相關系數僅為0.826，依據線性相關系數較高的式（11）和式（13），得到下式：

采用式（15）所示的均方根誤差（RMSE）和（16）的平均絕對誤差（MAE）兩個指標來評價式（12）和式（14）的計算結果，如表8 所示。

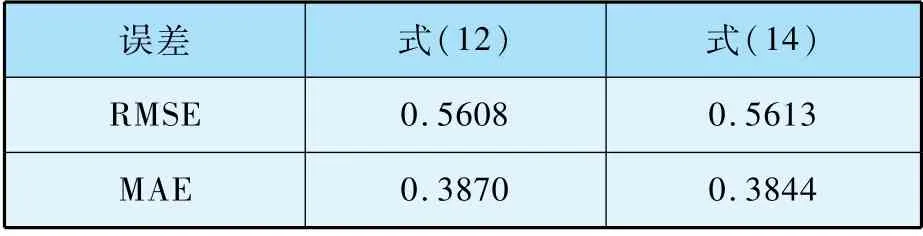
表8 不同計算公式的誤差比較

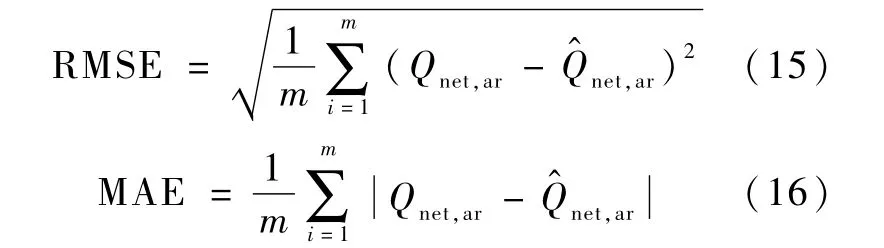
上式中，m 為樣本數量；Qnet，ar為發熱量實測值，MJ/kg；Q^net，ar為發熱量計算值，MJ/kg。

若使用RMSE作為衡量指標，式（12）計算結果較好；若使用MAE作為衡量指標，式（14）計算結果較好。

2.5 入爐煤質計算結果與化驗結果對比

配煤模型基于多目標的數學規劃問題，依據運行實際，對煤質參數賦予不同權重，在實現鍋爐對煤質參數要求的前提下，滿足不同配煤目標，輸出可供運行人員實際操作的供煤方案。 基于該實際方案，結合入廠煤到入爐煤流程的正向跟蹤和逆向溯源的方法，由入廠煤化驗的發熱量和揮發分等煤質數據，加上混煤煤質計算方法，預測得到皮帶入爐煤參數，如表9 所示。

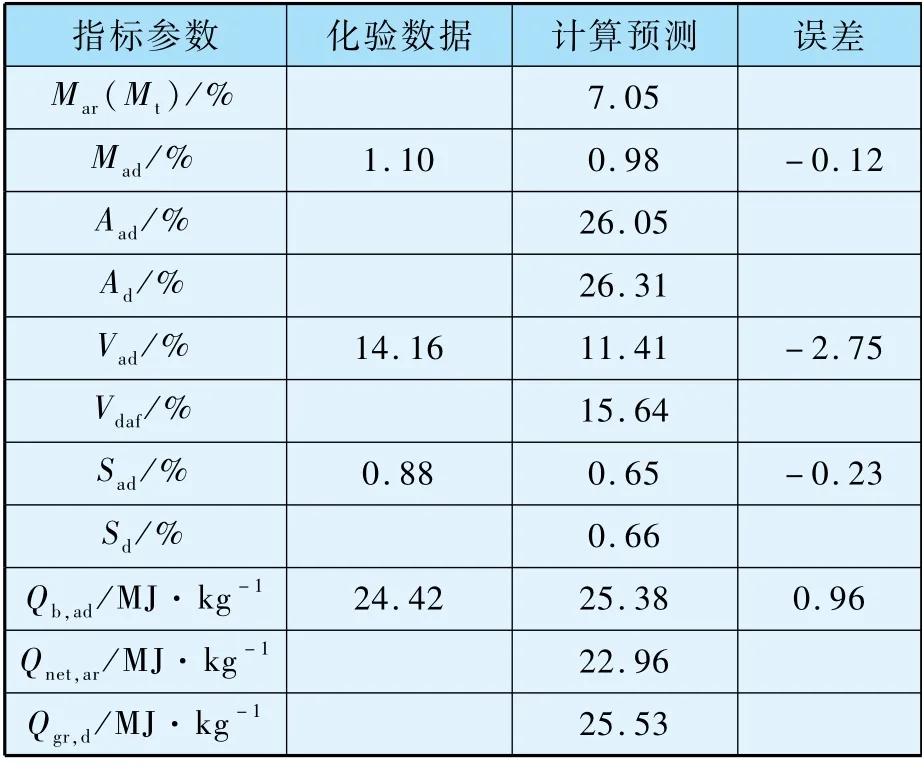
表9 入爐煤參數化驗值和預測值比較

顯然，預測結果得到的煤質參數更多，更全面，絕對誤差也較小。 更重要的是，在時間層面，預測結果相對于發布化驗結果可以提前10 余小時，很好地提高入爐煤獲取的實時性。

上述獲取入爐煤煤質的方法已經成功應用到電廠數據系統中，以低位發熱量為例，得到圖6 所示的一段時間內的預測值和化驗值的比較。

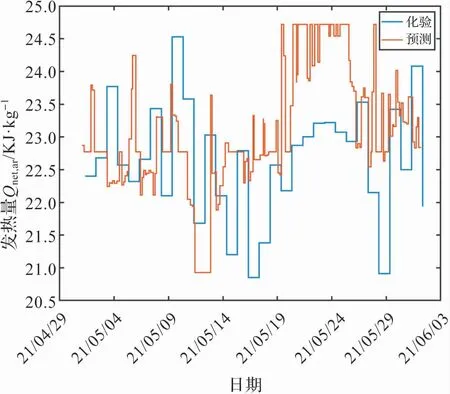
圖6 發熱量預測值和化驗值的比較

該系統將不斷增加的入爐煤化驗數據和預測結果間的誤差作為反饋，不斷修正預測模型和計算公式，使得預測值不斷接近化驗值。

3 總結與展望

針對某煤場過去依靠人工經驗配煤，缺乏可靠的配煤摻燒方案指導的問題，構建符合鍋爐燃燒對煤質要求的配煤模型。 依據不同配煤目標，輸出可實際操作的配煤方案，得到適用性較高的混煤煤質計算方法。 針對入爐煤化驗結果滯后，無法指導鍋爐運行的現象，提出全流程時空動態跟蹤來煤從入廠至入爐的環節。 利用配煤模型、入廠煤化驗數據和混煤煤質計算方法，計算得到入爐煤質參數。 與入爐煤實際化驗結果相比，不僅計算得到煤質參數更多、誤差較小，更可提前10 余小時獲知入爐煤質數據。 本文提出的基于動態跟蹤的理念，為電廠入爐煤煤質獲取提供一種新的思路。

需要指出的是，本文得到的入爐煤參數距離進入爐膛燃燒仍存在一定時間差，為了更準確監控煤質波動，為鍋爐運行調整提供預報信息，后續需要進一步研究制粉系統特別是原煤斗和磨煤機對入爐煤參數的影響。