強子夸克相變表面張力解析求解

周淑英 沈婉萍 毛鴻?

1)(杭州師范大學物理學院,杭州 311121)

2)(浙江大學物理系,杭州 310058)

最近一級相變動力學的研究在早期宇宙、致密星體和相對論重離子對撞實驗等方面得到了廣泛的關注,特別是與一級相變相關的引力波方面的研究,是當前宇宙學研究的熱點問題.本文利用有限溫度場論,在有限溫度和密度下,研究了Friedberg-Lee 模型下的單圈有效勢能和量子色動力學退禁閉相變的動力學機制,結果表明在全相圖中存在一級相變,在μ=0 MeV 時,臨界溫度 Tc =119.8 MeV;在T=50 MeV 時,臨界化學勢 μc=256.4 MeV.在薄壁近似下,通過液滴核合成唯象模型研究了均質氣泡成核的強子夸克一級相變的動力學過程,在適當的邊界條件下,求解場的運動方程,計算不同溫度和密度下氣泡臨界位形隨半徑的演化,獲得了表面張力、臨界半徑和核合成自由能等物理量隨溫度與夸克化學勢密度的變化關系.為了證明薄壁近似的可靠性和優勢,本文將薄壁近似的分析結果與相應的精確解進行了對比,討論了薄壁近似的適用條件,以及薄壁近似的優缺點等問題.雖然本文的計算結果是模型相關的,但是一般性的研發方法和結論具有普適性,所獲得的結果對其他領域一級相變動力學研究有較大的參考價值和現實意義.

1 引言

當溫度和重子數密度達到一定程度時,夸克和膠子將不再屬于某一個強子,而是形成一種新的物質狀態,即夸克膠子等離子體(quark-gluon plasma,QGP),目前正在運行的相對論重離子對撞實驗可以從實驗上揭示QGP 和強相互作用的物理特性.理論上,雖然量子色動力學(quantum chromodynamics,QCD)是描述強相互作用的基本理論,可以用來描述強子夸克相變的動力學,但由于色禁閉的存在,使得中低能非微擾區域QCD 的理論和數值計算都受到了極大地限制[1],因此,通常需要借助有效模型或理論來理解量子色動力學的非微擾性質,比如夸克介子模型(quark meson,QM)[2],Nambu-Jona-Lasinio(NJL)模型[3,4]、以及它們的Polyakov loop 拓展模型[5,6]等.

對于一級相變,亞穩態真空可通過氣泡核合成的機制隧穿至穩定真空,而氣泡的成核率等相變動力學的問題可利用標準的量子場論方法計算出來[7-11].另一方面,對于相變動力學機制的研究,有效勢能是一個十分重要和有效的理論工具.基于朗道的相變理論,在相變臨界區域,有效勢能可以按照系統序參量的階數進行展開,得到關于相變動力學機制的普適性特征,而不必太關注相變背后具體的物理背景和動力學過程.一般性而言,對于二級相變,通常保留序參量的二階項和四階項,不過對于一級相變,還需要加入非常關鍵的三階項,當然,如果要研究存在三相點的相變體系,比如存在過渡相變和一級相變的交叉點的問題,需要把有效勢能按照序參量展開成二階項、四階項和六階項的形式[12].所以,對于研究強相互作用一級相變的動力學問題,只要把系統的有效勢能按照序參量展開到二階、三階和最高階四階即可.從這個意義上講,Friedberg-Lee 模型及其衍生的模型對于研究一級相變動力學有著天生的優勢和得天獨厚的條件[13-15].當然,這里需要指出的是,利用該模型計算得到的結果從定量上看肯定是模型依賴的,但是關于一級相變動力學的定性結論卻是普適的和一般的,可被廣泛應用于宇宙學、凝聚態物理和致密星體等領域.

特別是在近期,一級相變動力學的研究越來越受到重視,在致密星體的研究中,可以通過引力波來研究混合中子星的一級相變下的物態方程,而在宇宙學中,一級相變被認為是引力波(GWs)的潛在來源之一,并且在不久的將來可能被直接探測到[16-18].另外,在早期宇宙的研究中,一級相變在弱電重子數核合成和暗物質的研究中也占據著非常重要的地位.對于強子夸克相變,由于對弱一級強子夸克相變的性質已經進行了大量深入的研究[19],利用薄壁近似,本文將采用解析的近似方法深入研究Friedberg-Lee 模型在有限溫度、有限密度下強一級強子夸克相變動力學機制,并與前期的數值結果進行比較,得到普適和一般性的結論[20].

本文首先簡要介紹了Friedberg-Lee 模型,然后基于有限溫度場論,給出了Friedberg-Lee 模型的有效勢能,并計算得出了相圖結構.通過介紹薄壁近似后計算得出穩定真空相氣泡的臨界位形、表面張力、臨界半徑和核合成自由能隨溫度與化學勢密度的變化關系,并將結果與精確解進行對比討論.

2 Friedberg-Lee 模型

1977 年Friedberg 和李政道提出Friedberg-Lee(FL)模型,在過去的數十年里,被廣泛應用于研究真空中單個核子的靜態物理性質,并取得了很大的成功[13-15,21].此外,在有限溫度場論框架下,該模型還被用于研究QCD 強一級退禁閉相變的熱力學和動力學性質[20,22-26].FL 模型的基本物理框架是把核子看成非拓撲孤子,通過引用唯象標量場σ來描述量子色動力學真空的非微擾特性,同時,該標量場代表核子內各個成分之間的相互作用,包括夸克之間、膠子之間以及夸克和膠子之間,直觀展示了夸克禁閉和退禁閉相變的物理特性.當系統處于真空態時,標量場σ的數值很大,使得組分夸克質量超過1 GeV,這時夸克就被囚禁在核子中.但隨著系統溫度或密度的升高,標量場σ的數值減小,并在臨界溫度處標量場有效值變為零,夸克變成了自由夸克,即實現了退禁閉相變的動力學過程.

FL 模型的拉格朗日密度表示如下:

方程(1)中,ψ表示自旋 1/2的u,d夸克場;σ就是唯象標量場,用以表征真空的非微擾特性;g為耦合常數;m為夸克的流質量,在FL 模型中取u,d夸克的流夸克質量為零;γμ為狄拉克矩陣.U(σ)為σ場的非線性自相互作用勢能,取到四次項:

對U(σ)求極值,可求得

其中σ0為局域最小值,對應為亞穩態真空(或稱為偽真空),此處的夸克的有效質量為零;而σv為絕對最小值,對應為穩定真空(或稱為真真空),此時夸克與σ耦合而得到非常大的有效質量gσv,從而實現夸克的禁閉.為使σv0,參數a,b,c需滿足b2＞3ac.將兩個真空的有效勢能之差記為ε,取U(0)=0,則真空態下口袋常數ε表示為

FL 模型中有4 個可調參數,分別為a,b,c,g.為了擬合這4 個參數,基于非拓撲孤子理論[27],先求得系統的Euler-Lagrange 方程:

在平均場近似條件下,將σ看作與時間無關的經典場:

考慮球對稱情形,用一組完備的狄拉克函數將夸克場算符展開:

其中夸克的基態波函數形式為

加上波函數歸一化條件為

對于核子,(13)式中的N取3.通過求解聯立的方程組(11)-(13),可以求得核子的質量、半徑、軸向向量常數和磁矩等物理量,并與實驗數值進行比較,從而確定模型的參數.選擇不同參數得到定量的物理結果會有所差異,但基本的物理圖像和結論不依賴于具體的參數.本文選取了一組在文獻中被廣泛采用的參數:a=17.70 fm-2,b=-1457.4 fm-1,c=20000,g=12.16,該組參數可以很好地擬合單個核子真空的物理性質[25].

3 Frieberg-Lee 模型的有效勢能及相圖

有效勢能是量子場論中的一個重要的理論工具,非常適合用來研究對稱性自發破缺和熱力學相變等物理問題.在有限溫度場論中[28,29],通過系統的巨配分函數,熱力學量都可以通過系統的巨正則勢能得到:

利用標準的有限溫度場論方法,FL 模型在有限溫度、有限密度下的單圈有效勢能形式如下:

其中β=1/T,μ是夸克數化學勢.VB(σ;β)是有限溫度下玻色子的單圈貢獻,VF(σ;β,μ)是有限溫度和密度下費米子的單圈貢獻.玻色項和費米項的具體形式是:

獲得系統的有效勢能之后,類比于MIT 口袋模型,FL 模型的口袋常數定義為亞穩態真空與穩定真空的有效勢能之差為

當體系的溫度和密度比較小的時候,亞穩態真空的能量大于穩定真空的能量,系統的口袋常數大于零,自由夸克被束縛在核子內部,而隨著溫度和密度的升高,這個口袋常數逐漸減小,并在T=Tc的時候,ε(T,μ)=0 .此時,意味著自由夸克將不再被囚禁在核子內部,從而變成了自由的夸克,進而實現了夸克的退禁閉相變.

圖1 給出了T-μ下FL 模型的退禁閉相變相圖結構.圖中的曲線為強子相和夸克相的臨界線,在曲線上,亞穩態真空和穩定真空的有效勢能相等,如果溫度繼續上升,兩個真空之間將實現了反轉.此外,對于FL 模型,在整個相圖的相變臨界點,由于兩個真空之間還被一個勢壘隔開,FL 模型只能給出強一級強子夸克相變.從圖1 可得到,任何溫度T下的臨界化學勢μc或任何化學勢μ下的臨界溫度Tc,可知在μ=0 MeV 時,臨界溫度Tc=119.8 MeV;在T=50 MeV 時,臨界化學勢μc=256.4 MeV.

圖1 FL 模型下的QCD 相圖結構Fig.1.QCD phase diagram structure under FL model.

4 薄壁近似下的核合成

對于典型的一級相變,當系統達到相變臨界溫度或臨界化學勢時,模型的熱力學有效勢能具有兩個相等的極小值,在這兩個極小值之間有一個勢壘將它們隔開.隨著溫度或化學勢的降低,兩個極小值將不再保持相等,其中,σ0 處的極小值稱為局域極小值,該數值較大,所以對應的真空定義為亞穩態真空,而σσv處的極小值為絕對最小值,對應的真空定義為穩定真空.亞穩態真空在經典物理中是穩定的,但在量子物理中,亞穩態真空有一定的概率通過量子隧穿效應變成穩定真空[30,31].

當T＜Tc或μ＜μc時,由熱漲落產生穩定真空的氣泡在亞穩態真空中可能增長也可能收縮,這取決于系統兩種能量之間的競爭.亞穩態真空中的體自由能密度高于穩定真空中的體自由能密度,因此,從亞穩態真空到穩定真空的轉變,即氣泡膨脹過程中,會降低整個系統的能量.但是,穩定真空的氣泡需要一個界面將穩定真空與亞穩態真空隔開,界面的表面張力使得整個系統的能量增大.因此,從亞穩態真空到穩定真空的相變機制取決于體系自由能密度與表面張力之間的競爭.穩定真空的氣泡的體自由能與R3成正比,兩真空相之間的表面張力與R2成正比,其中R為氣泡半徑.當R比較小的時候,兩個真空相直接的轉換使得整個體系的能量增大,氣泡將會收縮直至最終消失,反之,當R較大時,氣泡將不斷膨脹,直至占據整個系統,從而完成相變整個過程.所以是否能完成相變取決于氣泡半徑是否大于臨界半徑Rc,只有半徑大于臨界半徑Rc的氣泡在一級相變中起決定性作用.

根據液滴核合成模型的標準場論方法[7,8,10,32],對于FL 模型,系統自由能如下:

氣泡臨界位形是自由能函數對于標量場σ的一個極值解.將系統自由能F(σ)對σ進行變分,得到一個非線性常微分方程:

為了便于后續討論,通常將Veff(0;T,μ)固定為0.故系統單位時間、單位體積的臨界氣泡成核率可以表示為

其中T為系統的溫度,P通常近似表示為T4.亞穩態真空與穩定真空之間界面的表面張力定義為

對于一般的有效勢Veff,(22)式通常難以解析求解,一般要通過計算機求得該方程的數值解.但是對于數值求解,由于這是一個典型的兩點邊值二階微分方程,數值求解難度通常也很大,主要取決于猜測值是否合適,如果猜測值與實際值很接近,那么很容易得到正確的結果,但是如果猜測值與實際值相差較大,那么數值計算收斂性就很差,一般很難得到正確的結果.所以運氣和經驗對于數值求解孤子運動方程顯得尤為重要.當然,還有第二種方案可以選擇,就是求該運動方程的近似解.對于處于臨界狀態的系統,在TTc或μμc時,亞穩態真空和穩定真空的勢能之差ε遠小于隔開兩個真空的勢壘,此時穩定真空氣泡的半徑遠大于氣泡壁厚.在這種情況下,可以將(22)式中的第2 項舍去,則(22)式變為如下形式:

對其進行化簡,可得

兩邊進行積分,可得

可以發現,只要將(22)式中的第2 項舍去,即使沒有求解運動方程(22)式,也可以解析地得到體系運動方程的解,從而進一步得到系統的表面張力、鞍點解σb的場位形和臨界氣泡成核率等物理量.這種近似稱為薄壁近似(thin-wall approximation),被廣泛地運用于各種體系的一級相變動力學機制的研究中.

在薄壁近似的情況下,考慮到體自由能和表面張力的競爭,可以將半徑為R的氣泡的系統自由能表示為

其中Σ是亞穩態真空與穩定真空之間界面的表面張力,ε表示亞穩態真空與穩定真空的有效勢能之差.當F(R)為最小值時,氣泡有臨界半徑,對(29)式進行求導,可得臨界半徑Rc:

只有當穩定真空氣泡半徑大于臨界半徑Rc,才對系統一級相變起作用.

當ε=0 時,將(27)式代入(25)式,可求得薄壁近似下的表面張力表達式:

從(24)式可以看出指數因子對氣泡成核率有著重要影響,將(30)式代入(29)式,可得

運用(32)式可近似求解相變動力學的相關物理量,甚至不需要求解運動方程(22).所以薄壁近似是一個非常高效、快捷的研究方法.

5 近似解及其與精確解的討論

運用方程(28)可以得到不同溫度和化學勢密度下σ場隨半徑r的演化關系.圖2 分別繪制出了μ=0 MeV,T=0,70,100,105,109 MeV 及T=50 MeV ,μ=0,150,200,230,240 MeV 時的標量場σ場位形圖.

從圖2(a)可以看出,隨著半徑的增大,所有曲線都趨向于零,且穩定真空氣泡的半徑隨著溫度T的增大而增大,這一趨勢與文獻[20]中精確數值解的結論一致,只是近似解析解求得的氣泡半徑比精確數值解略小.此外,從圖2(a)還可以發現,當溫度T＜109 MeV 時,氣泡內部σ(0)的數值開始慢慢從σv偏離,并且隨著溫度的降低,σ(0)偏離σv越來越大,當溫度等于零的時候,σ(0)略微大于σv/2 .根據薄壁近似的結果,由(28)式不難得到,當溫度在臨界溫度或者非常接近臨界溫度的時候,對于0＜r＜R有σ(r)=σv,而對于r＞R,則σ(r)=0,這里R是穩定真空氣泡的半徑.所以從圖2(a)可知,當溫度小于 109 MeV 時,由于σ(0)開始偏離其預期值σv,說明此時表面薄壁近似的適用性有待重新評估.

對圖2(b)可做類似的分析,可以發現隨著化學勢μ的增大,所有曲線都趨向于零,且穩定真空氣泡的半徑隨著化學勢μ的增大而增大,但利用薄壁近似計算得到的半徑值略小于精確解.從圖2(b)可以看出,當化學勢μ＜230 MeV 時,σ(0)開始偏離其預期值σv,并且隨著化學勢的降低,σ(0)偏離σv的程度越來越大,故此時表面薄壁近似的適用性需要重新考慮.

圖2 (a)μ=0 MeV ,T=0,70,100,105,109 MeV 時氣泡臨界位形;(b)T=50 MeV ,μ=0,150,200,230,240 MeV時氣泡臨界位形Fig.2.(a)Bubble critical configuration at μ=0 MeV,T=0,70,100,105,109 MeV;(b)bubble critical configuration at T=50 MeV ,μ=0,150,200,230,240 MeV .

同樣,利用前面得到的有效勢能,根據(31)式可以計算薄壁近似下的氣泡表面張力.圖3 給出了在臨界溫度Tc下,夸克強子一級相變的表面張力隨化學勢密度μ的變化關系.從圖3 可以看出,當T=Tc時,強子相的表面張力隨著化學勢密度的增大而增大,溫度接近零度時,表面張力大約為14·73 MeV/fm2.

圖3 T=Tc 時表面張力隨化學勢 μ 的變化關系Fig.3.Surface tension as a function of chemical potential μwhen T=Tc.

運用同樣的方法,也可以計算出非臨界狀態下的表面張力,圖4 分別給出了μ=0 MeV 及T=50 MeV 時表面張力的變化.圖4(a)給出了μ=0 MeV 時表面張力與溫度的演化關系,隨著溫度T升高,表面張力先緩慢增長,當T＞60 MeV 時,表面張力快速增長,這與文獻[20]中的精確解得到的結果一致.不同的是,精確解給出的表面張力在T趨于 109 MeV 時快速增大,并在T=109 MeV 時達到最大值Σ(T)?7.38 MeV/fm2,在109 MeV＜T＜119.8 MeV 范圍內,表面張力隨著溫度的升高而減小.而薄壁近似給出的結果顯示,溫度接近于臨界溫度Tc=119.8 MeV 時,表面張力迅速增加,并在Tc=119.8 MeV 時達到最大值Σ(T)?9.17 MeV/fm2,大于精確解給出的臨界溫度時的表面張力.

圖4(b)給出了T=50 MeV 時表面張力與化學勢μ的演化關系,顯示出了相似的曲線,薄壁近似下表面張力隨著化學勢μ的增加而持續增加,并在臨界化學勢μc=256.4 MeV 時達到最大值Σ(T)?12.64 MeV/fm2;而對于精確解,表面張力的最大值出現在μ=230 MeV 處,其數值為Σ(T)?7.73 MeV/fm2,小于薄壁近似給出的近似解.可知,薄壁近似下,臨界化學勢下的表面張力大于精確解.

圖4 (a)μ=0 MeV 時表面張力與溫度 T 的關系;(b)T=50 MeV 時表面張力與化學勢 μ 的關系Fig.4.(a)Surface tension as a function of temperatureT when μ=0 MeV ;(b)surface tension as a function of chemical potential μ when T=50 MeV .

表面張力精確解與近似解的差別主要來源于運動方程的“阻力”項.對于薄壁近似,通常忽略了這一阻力項,而對于精確解,表面張力的大小不僅與有效勢Veff有關,還與有關,并且項對表面張力的影響大于有效勢Veff.從文獻[20]給出的臨界氣泡位形圖可以看出,當化學勢μ=0 MeV 時,在 0 MeV＜T＜109 MeV 范圍內,隨著溫度的升高而增大,因此表面張力在此溫度(0 MeV＜T＜109 MeV)范圍內一直單調遞增,但在109 MeV＜T＜119.8 MeV 范圍內,逐漸變小,因此表面張力從T=109 MeV 開始變小.故精確解結果是表面張力在T=109 MeV 時達到最大值,隨后減小.但是,薄壁近似下表面張力隨著溫度的降低單調遞減.

對T=50 MeV 的情況可做類似分析: 在溫度T=50 MeV 時,有效勢Veff隨著化學勢μ的升高而增大,故在薄壁近似下,表面張力呈現出單調遞增的趨勢;而對于精確求解情況,在溫度T=50 MeV時,當 0 MeV＜μ＜230 MeV 時,隨著溫度的升高而增大,因此在 0 MeV＜μ＜230 MeV 范圍內,表面張力一直單調遞增,但在230 MeV＜μ＜256.4 MeV 范圍內,逐漸變小,因此表面張力從μ=256.4 MeV 開始變小.故精確解結果是表面張力在μ=256.4 MeV 時達到最大值,隨后減小.

計算得到表面張力后,可利用(30)式分別計算出μ=0 MeV及T=50 MeV 情況下氣泡臨界半徑的演變關系,如圖5 所示.根據液滴核合成唯象模型,半徑小于臨界半徑的氣泡會在亞穩態真空中收縮并且消失,只有半徑大于臨界半徑的氣泡會增長并推動相變,因此半徑大于臨界半徑的氣泡在相變中起著決定性作用.

從圖5 可以看出,氣泡的臨界半徑隨著溫度或化學勢的升高,先緩慢增大,當趨近于臨界溫度或臨界化學勢時,氣泡的臨界半徑迅速增加至無窮大.這個現象可以根據(30)式作出解釋,當T→Tc或μ→μc時,亞穩態真空和穩定真空的有效勢之差ε→0,這導致了氣泡臨界半徑分散,該結果與精確解一致.

從亞穩態真空向穩定真空相變的過程會使系統自由能降低,薄壁近似下自由能的轉變可由(32)式算出.從(24)式可以看出指數因子Fb/T對氣泡成核率有著重要影響,圖6 分別繪制了μ=0 MeV及T=50 MeV下Fb/T的演變關系.

從圖6(a)可以看出,當μ=0 MeV 時,Fb/T隨著溫度升高先減小后增大,在接近臨界溫度時迅速增大至發散.當T?114.5 MeV 時,Fb/T≈1,則成核率Γ將受到指數因子Fb/T的強烈抑制,系統將會在亞穩態真空中保持較長的時間.當系統溫度T＜114.5 MeV .從圖5(a)也可以看出,當溫度T＜114.5 MeV 時,臨界半徑Rc很小,任何半徑大于臨界半徑的氣泡都將膨脹完成亞穩態真空到穩定真空的相變,而當114.4 MeV＜T＜119.8 MeV時,臨界半徑Rc迅速增大并發散,任何半徑小于臨界半徑的氣泡都將收縮并消失,故此時成核率受到抑制.

圖5 (a)μ=0 MeV 時臨界半徑與溫度 T 的關系;(b)T=50 MeV 時臨界半徑與化學勢 μ 的關系Fig.5.(a)Typical radius of the critical bubble as a function of temperature T when μ=0 MeV ;(b)typical radius of the critical bubble as a function of chemical potential μ when T=50 MeV .

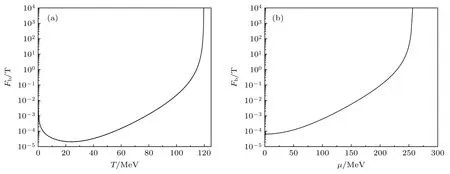
圖6 (a)μ=0 MeV時Fb/T 與溫度 T 的關系;(b)T=50 MeV時Fb/T 與化學勢 μ 的關系Fig.6.(a)Fb/T as a function of temperature T when μ=0 MeV;(b)Fb/T as a function of chemical potential μ when T=50 MeV.

針對圖6(b)中T=50 MeV 的情況可做類似分析,從圖6(b)可以看出,當T=50 MeV 時,Fb/T隨著化學勢升高單調遞增,在接近臨界化學勢時迅速增大至發散.當μ?229.4 MeV 時,Fb/T≈1,成核率Γ受到指數因子Fb/T的強烈抑制,系統將會在亞穩態真空中保持較長的時間.從圖5(b)也可看出,當化學勢μ＜229.4 MeV 時,臨界半徑很小,任何半徑大于臨界半徑Rc的氣泡都將膨脹完成亞穩態真空到穩定真空的相變,而當229.4 MeV＜μ＜256.4 MeV 時,臨界半徑Rc迅速增大并發散,任何半徑小于臨界半徑的氣泡都將收縮并消失,故此時成核率受到抑制.上述結果與精確解保持一致.

6 總結

基于Frieberg-Lee 模型,本文采用薄壁近似,通過液滴核合成唯象模型研究了均質氣泡成核的強子夸克一級相變的動力學過程,并將薄壁近似得到的結果與精確解進行了比較和討論,同時給出了Friedberg-Lee 模型的相圖.

在化學勢μ=0 MeV 時,氣泡表張力呈現遞增趨勢,表面張力最大值為Σ(T)?9.17 MeV/fm2,近似結果略大于精確解結果,同時解釋了兩者存在差別的原因.此外發現μ=0 MeV 時氣泡臨界半徑Rc與溫度T的演化關系是先緩慢增大,臨近臨界溫度時迅速增大至發散,而μ=0 MeV時Fb/T與溫度T的演化關系是先減小后增大,在接近臨界溫度時迅速增大至發散.進一步,對于T=50 MeV的情況進行了分析,在此情況下,氣泡表面張力也呈現遞增趨勢,最大值為Σ(T)?12.64 MeV/fm2.本文還給出了T=50 MeV 時氣泡臨界半徑Rc與化學勢μ的演化關系是先緩慢增大,而T=50 MeV時Fb/T與化學勢μ的演化關系是持續增大,兩者在接近臨界化學勢時均迅速增大至發散.

表面張力在QCD 相變、宇宙學和致密星體的研究中有重要作用,被廣泛關注和討論.在合適的邊界條件下,數值求解方程(22)是一個典型的兩點邊值問題,求解此類問題最關鍵的是找到方程解的猜測值,猜測值與真實值越接近,方程越容易求解,反之則很困難.此外,由于存在數值計算的不確定性,對于某些溫度,找到正確的精確解仍是一個挑戰,故難以求得整個相圖的表面張力.考慮到精確數值求解運動方程的困難,通常可以采用薄壁近似來解析求解該運動方程,從而得到表面張力、臨界半徑和系統自由能的近似值,通過與精確解析結果的比對,發現即使溫度低于或者遠小于臨界溫度,解析解與數值解的差別也不大,說明對于一級相變的大部分問題,都可以采用薄壁近似來處理,進而可以避開難以求解的兩點邊值問題.此外,對于缺乏精確解,只有近似解的模型,如QM 模型和PQM 模型(Polyakov-quark-meson model),知道近似解和精確解之間的差別是十分重要的,本文利用FL 模型討論發現,雖然近似解會抹掉一些重要的信息,比如表面張力隨溫度變化的非線性行為,但在定性的結論上兩者差別并不是很大,這從側面反映出其他模型的近似解和精確解在定性結論上的差異.

此外,通過比對解析解和數值解的場位形,對于那些一定需要精確求解的物理體系,解析解也可以作為精確求解方程的猜測值,從而更容易得到收斂的數值解.比如對于QM 模型、NJL 模型以及其拓展模型,通常數值求解運動方程非常困難,薄壁近似有助于更快得到精確的數值解,目前所有的這些研究工作正在進行中.