一種與開放系統初態無關的非馬爾科夫度量*

賀志 蔣登魁 李艷

1)(湖南文理學院數理學院,常德 415000)

2)(南昌師范學院物理與電子信息學院,南昌 330032)

近年來,量化開放量子系統中的非馬爾科夫效應已經成為了量子消相干控制領域研究中的一個重要科學問題.本文對于單個開放的兩能級系統,將基于量子Fisher 信息的非馬爾科夫度量從系統初態為純態的情況推廣到系統初態為任意態的情況.作為該非馬爾科夫度量的應用,分別研究了利用量子Fisher 信息在檢測一個兩能級系統受到零溫度振幅耗散通道、相位衰減通道和隨機幺正通道作用時對應非馬爾可夫過程發生滿足的條件.研究結果顯示: 一個相位參數的量子Fisher 信息對這三種衰減通道的非馬爾科夫過程發生所滿足的條件與系統初態的選擇是無關的.進一步,對于振幅耗散通道和相位衰減通道,非馬爾科夫過程發生的條件同基于跡距離、映射的可分性、量子互信息和量子Fisher 信息矩陣等給出的條件是等價的.如預期的一樣,對于振幅耗散通道情況且選擇系統初態為最優化純態時,相應的結果正是Lu 等獲得的結果(Lu X M,Wang X G,Sun C P 2010 Phys.Rev.A 82 042103);而對于隨機幺正通道,其馬爾可夫過程發生的條件同基于跡距離、映射的可分性、量子互信息和量子Fisher 信息矩陣等給出的條件是不完全等價的.另外,得到了一個有趣的關系: 在這三種耗散通道模型中系統演化態的量子 l1 范數相干性的平方正好等于相位參數的量子Fisher 信息.總之,本文得到的結果不僅完善了用量子Fisher信息來檢測開放系統中非馬爾科夫效應的應用范圍,同時也進一步彰顯了量子Fisher 信息在量子信息處理中獨特的作用.

1 引言

在量子消相干控制領域研究中,假設環境沒有記憶效應,開放量子系統的信息或能量只能單方向流入外界環境,這個過程常被稱為馬爾科夫過程;相反地,如果環境有記憶效應,則系統流入外界環境的信息或能量在某段時間還能流回系統,此過程常被稱為非馬爾科夫過程.開放量子系統中的這種非馬爾科夫效應將會使得系統的信息和能量的衰減得以延緩.在真實的量子信息處理中,實際的環境一般都具有記憶效應,所以研究開放系統中的非馬爾科夫效應顯得十分必要[1-5].研究表明: 開放系統中的非馬爾科夫效應對量子信息處理有諸多積極的影響.如利用環境的非馬爾科夫效應可延長兩量子比特的糾纏時間[6-8]、保護原子熵壓縮[9-11]、以及提高量子Fisher 信息[12,13]等.自然地,怎樣去量化開放系統中的非馬爾科夫效應就成為了一個很有趣的研究課題.近 10 多年來,在理論上相繼有許多優秀的非馬爾科夫度量被提出,如基于跡距離[14-16]、映射的可分性[17]、量子Fisher 信息[18]和量子互熵[19]等就是幾種非常流行的非馬爾科夫度量方式,且部分已在實驗上被證實[20,21].在現有的非馬爾科夫度量中,從不同的角度出發大概可以分成三大類: 1)基于一些物理量[14,18,22-32]在跡保守且完全正定映射下是非增的性質;2)從系統經歷的動力學映射的可分性[17,33-35];3)考慮在一個有輔助系統的大系統中基于一些物理量[19,36-40]在跡保守且完全正定映射下具有非增的性質.

然而,當將這些非馬爾科夫度量應用到具體模型時不難發現,只有部分非馬爾科夫度量在檢測非馬爾科夫效應時的有效性與系統初態選擇是無關的.早在2011 年,Zeng 等[41]已經闡明,利用基于跡距離的非馬爾科夫度量[14]在檢測零溫度振幅耗散模型和相位衰減模型中的非馬爾科夫效應時,與系統初態選擇有關的要求可以被移除,但不影響其檢測的有效性.近來,有部分基于量子相干性的非馬爾科夫度量被揭示在檢測非馬爾科夫效應時的有效性也同系統初態選擇是無關的,如量子l1范數相干性[28]、基于skew 信息和修改的Tsallis 相對α熵的相干性[30]、基于保真度和幾何度量相干性[32]等.可是,也有相當一部分非馬爾科夫度量的有效性與系統初態選擇是有關的,如基于量子糾纏[17]、量子互信息[19]、最大相對熵[29]、Hilbert-Schmidt speed(HSS)[31]、量子局域不確定度[36]及量子相對熵相干性[40]等.Lu 等[18]基于量子Fisher 信息流定義了一種非馬爾科夫度量,并運用其去檢測零溫度振幅耗散模型的非馬爾科夫效應.后來,Song 等[26]基于兩參數的量子Fisher 信息矩陣定義了一種非馬爾科夫度量.然而,這兩個文獻中考慮的都是假設系統初態為純態的情況.那么,一個問題可能被提出: 基于量子Fisher 信息的非馬爾科夫度量在檢測非馬爾科夫效應時的有效性是否與系統初態選擇有關? 另外,該非馬爾科夫度量與系統初態選擇無關的特性是否取決于考慮的耗散模型? 這些問題是促使本文研究的主要初衷.

本文在文獻[18]的基礎上,假設一個開放兩能級系統初態為任意量子態,將基于量子Fisher 信息的非馬爾科夫度量運用到三種常見的耗散通道--零溫度振幅耗散通道、相位衰減通道和隨機幺正通道中,得到了對應非馬爾可夫過程或馬爾可夫過程發生的條件,并同其他非馬爾科夫度量作了詳細的比較.研究發現: 基于量子Fisher 信息的非馬爾科夫度量在這三種耗散通道中的有效性同系統初態的選擇是無關的.特別地,對于振幅耗散通道模型,如果選擇系統初態為文獻[18]中考慮的純態,相應結果簡化成文獻[18]中的特殊情況.當然,對于相位衰減通道模型,其非馬爾科夫過程發生的條件同用跡距離、映射的可分性、量子互信息和量子 Fisher信息矩陣給出的條件是等價的.然而對于隨機幺正通道模型,通過對通道的一些具體參數進行討論,發現其馬爾可夫過程發生的條件同基于跡距離、映射的可分性、量子互信息和量子Fisher 信息矩陣給出的條件是不完全等價的.另外,也揭示了在這三種耗散通道模型中量子Fisher 信息與相干性之間的一個密切關系,即系統演化態的量子l1范數相干性的平方正好等于相位參數的量子Fisher 信息.因此,本文得到的結果可能為開放系統中非馬爾科夫動力學研究提供了一種與系統初態無關的非馬爾科夫度量,進一步強化了量子Fisher 信息在量子信息處理中的獨特作用.

本文結構安排如下: 第2 節利用量子Fisher信息在跡保守且完全正定映射下具有非增性的性質構建了一種非馬爾科夫度量;第3 節給出了將基于量子Fisher 信息的非馬爾科夫度量用于三種典型的耗散通道模型中的非馬爾科夫過程或馬爾科夫過程發生的條件,并詳細討論了同其他非馬爾科夫度量給出的條件之間的等價性問題;第4 節對文中獲得的結果作了簡要總結和展望.

2 基于量子Fisher 信息的非馬爾科夫度量的構建

量子Cramér-Rao 不等式[42]揭示了量子Fisher信息是刻畫單個待估計參數達到最優理論精度的一個物理量,它已經成為了量子度量學的核心概念之一.根據量子Cramér-Rao 不等式,對某一個待估計參數θ測量的精度由下面的不等式[42]決定:

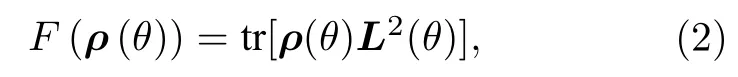
其中ρ(θ)是系統包含待估計參數θ的厄米算符,L(θ)是一個厄米算符,常被稱為對稱對數導數(symmetric logarithmic derivation,SLD),并由下列方程決定:

方程(2)和方程(3)定義的量子Fisher 信息F(ρ(θ))是量子信息理論中一個非常重要的物理量,它具有許多優良的物理性質[18,43]:

1)具有在非參么正演化U(UU?=U?U=I)下不變性:F(ρ(θ))=F(Uρ(θ)U?);

2)具有在跡保守且完全正定映射Φt下非增性(或者被稱為收縮性(contractivity)):F(Φtρ(θ))≤F(ρ(θ));

3)具有直積可加性:F(ρ(θ))=,其中ρ(θ)=;

4)具有凸性:F(ρ(θ))≤,其中ρ(θ)=,λi是子系統ρi(θ)所占的比重.

特別地,量子Fisher 信息F(ρ(θ))同量子信息理論中其他一些重要的度量像保真度f(ρ1,ρ2)=有著密切的聯系,如[44]ξ=?2f(ρ(θ),ρ(θ+δθ))/?(δ2θ)=Fθ/4,其中ξ是保真率.這進一步印證了量子Fisher 信息在量子信息領域中扮演著一個極其重要的角色.

在量子消相干的主方程框架下,如果一個開放系統的動力學可以用一個跡保守且完全正定映射來描述,就表明開放系統經歷了一個馬爾科夫過程[1,14].因此,這個完全正定映射在某個時間段的違反就可用來表征此時開放系統經歷了一個非馬爾科夫過程.考慮到量子Fisher 信息F(ρ(θ))在一個跡保守且完全正定映射下具有非增的性質,那么它在某段時間上的違反就可以被用來檢測開放系統在這段時間上非馬爾科夫過程的發生.為此,基于量子Fisher 信息的非馬爾科夫性(non-Markovianity)能被定義為

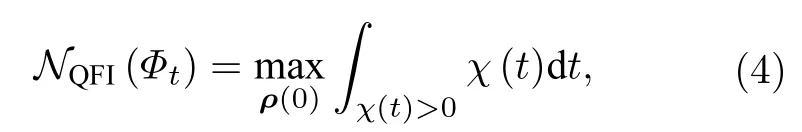
其中定義χ(t)=dF(ρ(θ))/dt,最大化(“max”)取遍系統所有的初態.明顯地,χ(t)≤0 對應馬爾科夫過程;χ(t)＞0 對應非馬爾科夫過程.文獻[18]建議了一種類似的非馬爾科夫度量,相應的χ(t)被命名為量子Fisher 信息流(其中χ(t)＞0 表示量子信息流是向內的,對應非馬爾科夫過程;χ(t)＜0表示量子信息流是向外的,對應馬爾科夫過程),他們具體研究了用系統初態為純態的量子Fisher 信息來見證一個零溫度振幅耗散通道模型中非馬爾科夫過程的發生.

本文在文獻[18]的啟發下,嘗試將方程(4)中對于最大化的要求移除,但不影響用量子Fisher信息來檢測非馬爾科夫過程的有效性.通常地,在研究開放系統中的非馬爾科夫過程時,尋找一種與系統初態選擇無關的非馬爾科夫度量方式不管是理論研究還是實驗角度看都是十分重要的.其原因是: 一方面,只需要關注系統受到外界環境的影響而不需要關心系統自身的量子態;另一方面,它也降低了在實驗上驗證開放系統中非馬爾科夫效應對于系統初態制備的要求,簡化了實驗的操作性.下面,首先用基于量子Fisher 信息的非馬爾科夫度量(如方程(4)所示)來重新考察一個二能級系統經歷一個零溫度振幅耗散通道作用時其非馬爾科夫過程發生的條件.有趣的是,研究表明: 對于零溫度振幅耗散通道模型,方程(4)中對于最大化的要求確實可以被移除,而不影響其測度非馬爾科夫過程的有效性.相應地,文獻[18]中考慮系統初態為純態的情況是這里的一種特殊情況.進一步,我們研究了基于量子Fisher 信息的非馬爾科夫度量在其他非馬爾科夫衰減通道,如相位衰減通道和隨機幺正通道模型中的表現,發現也有類似的特點.

接下來,當討論各種具體的非馬爾科夫耗散模型中某個參數估計問題時,必然要涉及到量子Fisher 信息的計算問題.一般來說,量子Fisher 信息F(ρ(θ))的計算在系統密度矩陣的本征空間中操作是方便的.根據文獻[45],在系統的密度矩陣對角化形式,如ρ(θ)=(其中M表示所有非零本征值λi(θ)對應的本征態|ψi(θ)〉構成的子空間,也被稱為支集(support)的維 度)下,量子Fisher 信息F(ρ(θ))表示如下:

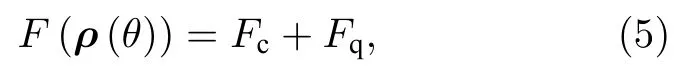
其中

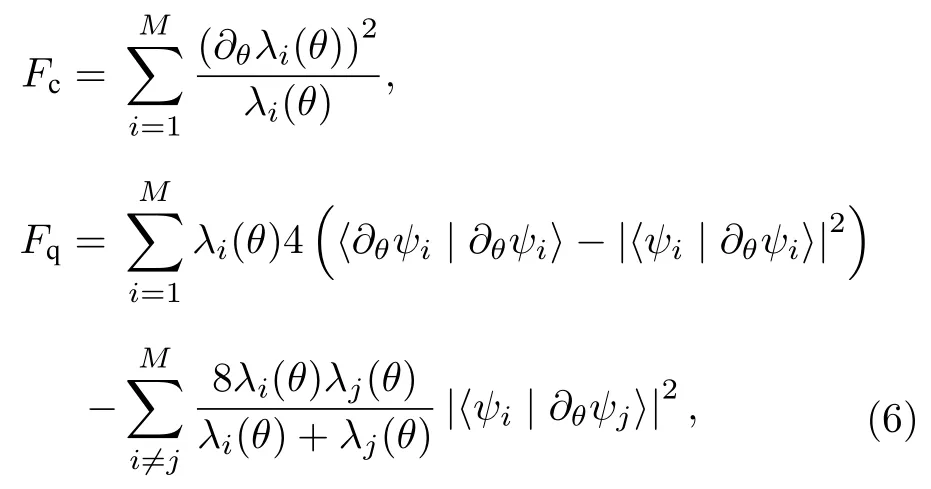
分別代表只與密度矩陣本征值有關的經典貢獻和與本征態有關的量子貢獻.考慮到M≤d(假設密度矩陣的總維度為d),那么,量子Fisher 信息F(ρ(θ))如方程(5)和方程(6)所示的表達式對任意秩的密度矩陣都是成立的.特別地,對于純態,也就是M=1(對應λ1(θ)=1)的量子Fisher 信息F(ρ(θ))退化成

特別地,文獻[46]給出了單個封閉和開放量子比特系統在布洛赫球表示,如ρ(θ)=1/2(1+ω·σ)(其中ω=(ωx,ωy,ωz)T表示布洛赫矢量,σ=(σx,σy,σz)表示著名的泡利矩陣)中量子Fisher 信息的計算表達式:

其中FC(ρ(θ))代表單個封閉量子比特系統的量子Fisher 信息,FO(ρ(θ))代表單個開放量子比特系統的量子Fisher 信息,ε表示一個量子噪聲的動力學映射,它在量子態上作用可以用Kraus 算符形式來表達,如ε(ρ)=.

3 應用到三類典型的非馬爾科夫耗散通道模型

3.1 非馬爾科夫零溫度振幅耗散通道

首先,注意到文獻[18]研究了利用一個相位參數的量子Fisher 信息去量化一個二能級系統受到一個零溫度振幅耗散通道作用的非馬爾科夫效應.文中的這個相位參數測量估計的方案是: 一個二能級系統最初處在最優化純態 |ψin〉=|ψopt〉=(|g〉+|e〉)/(|g〉+|e〉)/(這里,|g〉,|e〉分別表示二能級系統的基態和激發態);然后在 |ψopt〉 執行一個量子比特相位門,如Uθ=|g〉〈g|+exp(iθ)|e〉〈e|(引入相位參數θ);最后,假設這個相位參數進行測量估算之前系統受到了一個零溫度振幅耗散通道作用.本文研究的方案同文獻[18]是類似的,唯一不同的是這里考慮在基矢 {|e〉,|g〉}下系統最初處于一個一般量子態情況,如

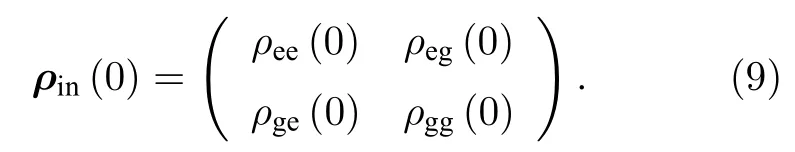
這樣,不難得到系統在經過量子比特相位門作用后的量子態如下:

接下來,這個二能級系統受到一個零溫度振幅耗散通道作用時其動力學演化滿足下列主方程[1]:

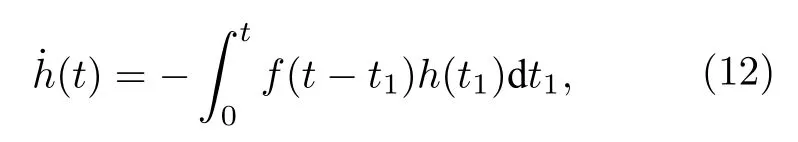
其中,初始條件有h(0)=1,記憶核f(t-t1)=是與零溫度熱庫的譜密度J(ω)有關的函數.這樣在任意時刻t,系統的密度算符能夠表示為

最后,利用方程(7)或方程(8),通過直接的代數運算獲得待測參數θ的量子Fisher 信息F(ρ(θ))為

像預期的一樣,當考慮系統最初處在最優化純態 |ψin〉=|ψopt〉=,即ρeg(0)=1/2,且h(t)為實數時,量子Fisher 信息F(ρ(θ))恰好簡化成文獻[18]中的結果,即F(ρ(θ))=h2(t).

這樣,根據方程(4),對于基于量子Fisher 信息的非馬爾科夫性能夠表示如下:

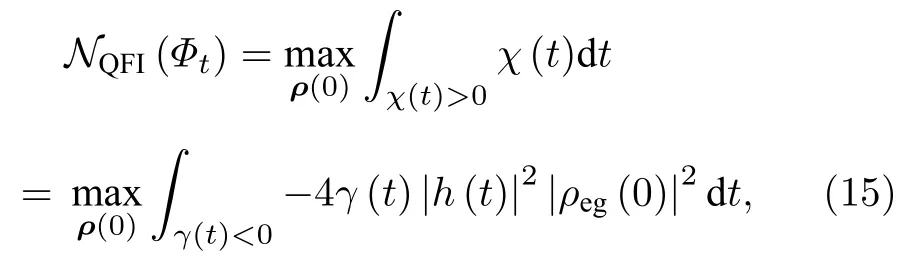
其中含時的衰減率γ(t)=.等價地,相應非馬爾科夫過程發生的條件可以用下列關系式來表示:

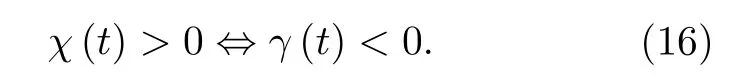
方程(16)清楚地顯示: 用量子Fisher 信息見證零溫度振幅耗散模型中非馬爾科夫過程發生的條件,即γ(t)＜0,同其他非馬爾科夫度量,如跡距離[47]、映射的可分性[47]、量子互熵[48]及量子Fisher 信息矩陣[26]給出的條件是相同的.另外,觀察方程(15)不難發現一個值得注意的特征,即方程(15)最大化的要求其實可以被移除,但不影響它見證非馬爾科夫過程的有效性.換句話說.用量子Fisher 信息來檢測非馬爾科夫過程發生的有效性或靈敏度是與系統初態的選擇無關的.對于零溫度振幅耗散模型,也存在一些與系統初態選擇無關的非馬爾科夫度量,如基于跡距離[41]和量子l1范數相干性[28]等.以上研究結果顯示,利用量子Fisher 信息可以提供一種可選擇的與系統初態無關的非馬爾科夫度量.注意到,文獻[18]中考慮的系統最初處在最優化純態 |ψin〉=|ψopt〉=(|g〉+|e〉)/,即ρeg(0)=1/2,正好是使得方程(15)取得最大值的初態.而我們的結果延伸了文獻[18]的結果,將系統初態為純態的情況推廣到了任意混合態的情況,這是本文獲得的主要結果之一.為了進一步直觀顯示基于量子Fisher 信息的非馬爾科夫度量是否與同系統初態有關,圖 1 給出了在不同系統初態下NQFI隨參數λ的變化關系.對于零溫度振幅耗散通道模型,這里假設二能級系統的本征頻率與環境庫的中心頻率是相同的即共振情況,且環境庫的譜密度是洛倫茲譜密度[1]

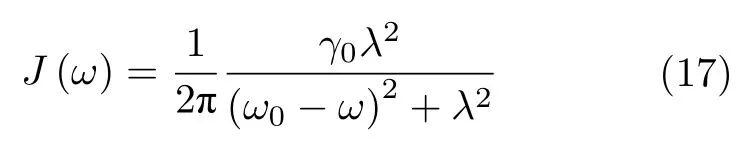
時,h(t)存在下列的解析表達式[1]:

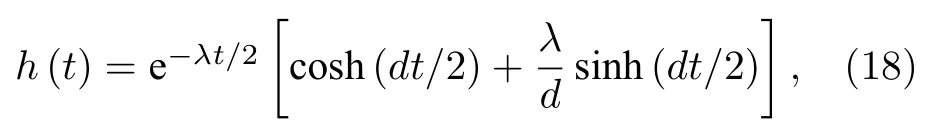
其中d=,λ表示耦合的譜寬度,它與環境庫的關聯時間尺度τB的關系為τB=λ-1;γ0表示系統和環境的耦合強度,它與系統的弛豫時間尺度τR的關系為τR=.從圖 1 可以明顯地看到,對于不同系統初態(如|ρeg(0)|=3/10→2/5→1/2),雖然NQFI的初始值有所不同,但它們隨λ的增加呈單調遞減的關系,以及變化趨勢都是相同的.這與之前得到的結果也完全符合: 基于量子Fisher 信息的非馬爾科夫度量在見證零溫度振幅耗散通道模型中非馬爾科夫過程時的有效性確實與系統初態選擇是無關的.另外,對于不同的系統初態,NQFI之所以隨λ的增加而單調遞減,其原因是: 耦合的譜寬度λ與環境庫的關聯時間尺度τB有以下關系:τB=λ-1,這樣,越大的λ意味著環境庫的關聯時間越短,從環境庫流回系統的信息或能量就會越少,從而導致非馬爾科夫效應,即NQFI隨λ的增加而單調遞減.

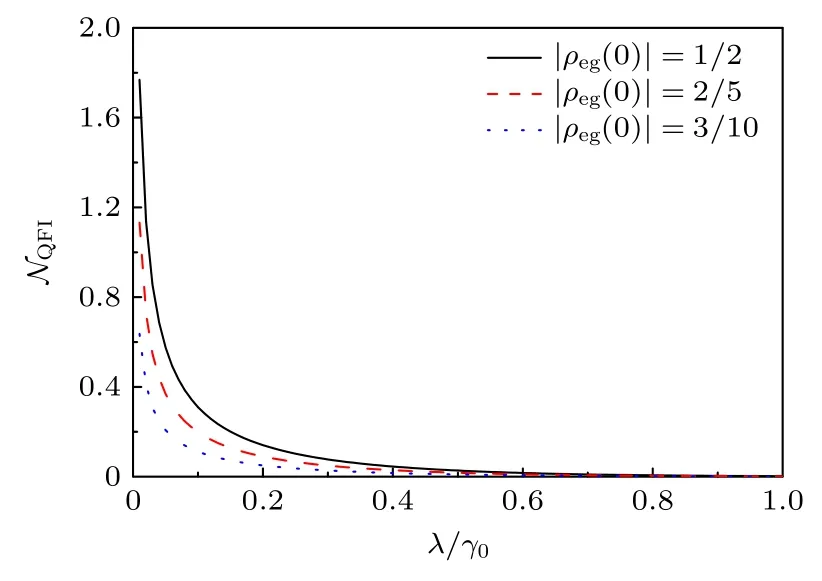
圖1 在不同系統初態(這里用不同初態對應的非對角元值 |ρeg(0)| 來表示)下 NQFI 隨參數 λ 的變化Fig.1.Non-Markovianity NQFI as a function of λ for different initial states of system denoted by their off-diagonal elements |ρeg(0)|.

3.2 非馬爾科夫相位衰減通道

本節繼續研究利用一個相位參數的量子Fisher 信息來量化一個二能級系統受到一非馬爾科夫相位衰減通道作用時其非馬爾科夫效應問題.類似于3.1 節對于處理非馬爾科夫零溫度振幅耗散通道的方案,假設一個二能級系統受到一非馬爾科夫相位衰減通道作用之前處在方程(10)所示的量子態.而一個二能級系統在經歷一個非馬爾科夫相位衰減通道作用時,系統的密度算符的演化遵循下列的主方程[1]:

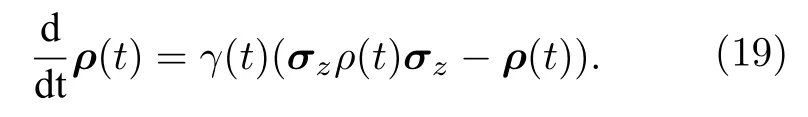
因此,處于方程(10)所示量子態的二能級系統按方程(19)所示的規律演化,最終該二能級系統在任意時刻t的密度算符能夠被寫成:

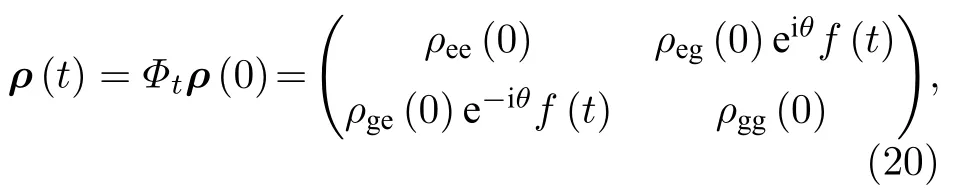
其中f(t)=.根據方程(7)或方程(8),通過一些簡單的計算,不難得到相位參數θ的量子Fisher 信息為

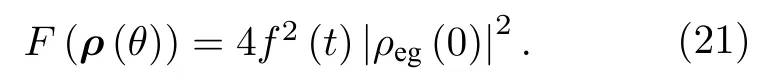
相應地,根據方程(4),基于量子Fisher 信息的非馬爾科夫性能夠被獲得如下:

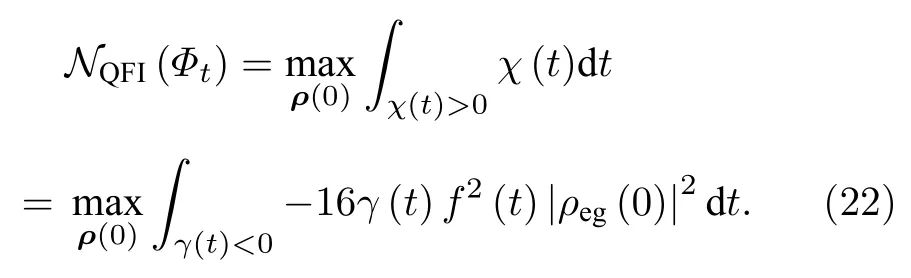
顯然,對于相位衰減通道中非馬爾科夫過程發生的條件χ(t)＞0 等價于γ(t)＜0.這個非馬爾科夫條件與用其他非馬爾科夫度量,如跡距離[47]、映射的可分性[47]、量子互熵[48]及量子Fisher 信息矩陣[26]等給出的條件是相同的.類似地,在方程(22)中的最大化的要求也可以被移除,而不影響用量子Fisher 信息來測度非馬爾科夫過程的有效性.

3.3 非馬爾科夫隨機幺正通道

進一步,考慮當一個二能級量子系統與一個隨機幺正通道相互作用模型,該系統的動力學演化可以用下列唯象的主方程[47]來描述:

這里,γi(t)(i=1,2,3)表示含時的衰減系數,σi(i=1,2,3)表示著名的泡利矩陣.明顯地,隨機幺正通道模型是相位衰減通道模型的一個推廣模型,即它除了考慮相位衰減通道模型中σz(σ3)以外,同時還考慮了σx(σ1)和σy(σ2)的影響.

等價地,主方程(23)可以寫成以下兩種表示形式:

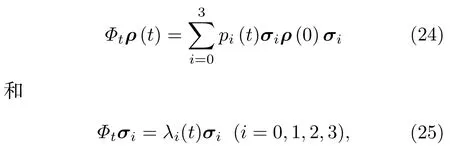
這里,σ0=I,pi(t)≥0 以及=1.特別地,在t=0 時,由Φ0=I得到p0(0)=1 以及pi(0)=0(i=1,2,3).另外,方程(24)和方程(25)中的參數pi(t)和λi(t)之間有下列關系:

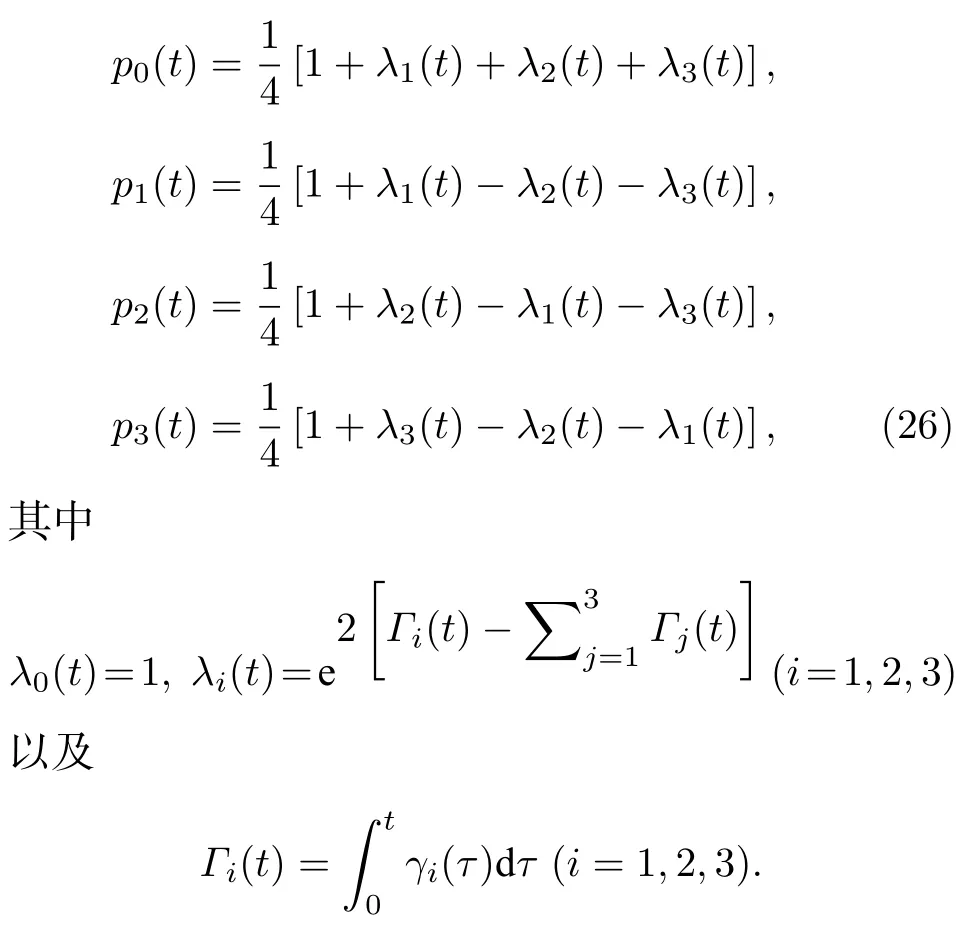
注意到,方程(25)揭示了隨機幺正通道作用在泡利矩陣上的運算規則,那么系統的初態被選擇成布洛赫球形式比較方便,這樣,系統在經歷隨機幺正通道作用之前的態可表示成

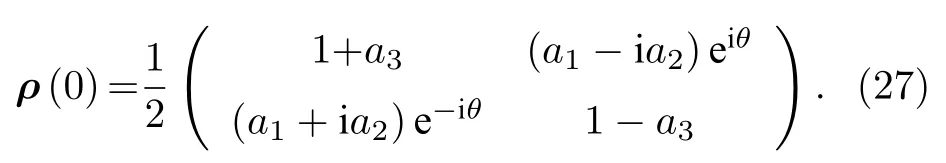
在方程(25)所示的映射作用下,系統在任意時刻t的態可被獲得如下:

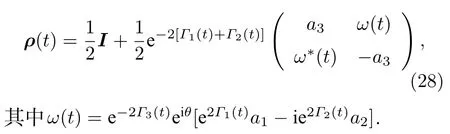
利用方程(7)或方程(8),可以給出相位參數θ的量子Fisher 信息的解析表達式如下:

因為隨機幺正通道涉及到多個通道情況,其非馬爾科夫過程發生的條件有點復雜,現在大多數文獻研究這個模型的時候都集中在馬爾科夫條件上.因為一旦馬爾科夫條件中某個子條件被違反,則意味著系統動力學是非馬爾科夫的.對于相同的隨機幺正通道,Chruscinski 和Wudarski[47]研究顯示,基于跡距離和映射的可分性的馬爾科夫條件是不完全等價的;Jiang 和Luo[48]研究顯示,基于量子互熵、跡距離以及映射的可分性的馬爾科夫條件是不完全等價的;Song 等[26]研究顯示,基于量子Fisher信息矩陣、量子互熵和跡距離的馬爾科夫條件是不完全等價的.He 等[40]研究顯示,基于量子相對熵相干性、跡距離、映射的可分性以及量子互熵的馬爾科夫條件也是不完全等價的.所以,這里也只研究該模型中基于量子Fisher 信息的馬爾科夫條件.從方程(30)容易得到,基于量子Fisher 信息的馬爾科夫條件χ(t)≤0 等價于當且僅當γ2(t)+γ3(t)≥0和γ1(t)+γ3(t)≥0.明顯地,該馬爾科夫條件同基于跡距離的馬爾科夫條件(如當且僅當γ1(t)+γ2(t)≥0,γ1(t)+γ3(t)≥0,γ2(t)+γ3(t)≥0)、基于映射的可分性的馬爾科夫條件(如當且僅當γ1(t)≥0,γ2(t)≥0,γ3(t)≥0)是不完全等價的.為了更具體地同其他非馬爾科夫度量的馬爾科夫條件進行比較,這里主要考慮一類特殊情況:pi(t)=αi(1-p0(t))(i=1,2,3),且α1=α2=α,α3=1-2α(α∈[0,1/2]).那么,基于量子Fisher 信息的馬爾科夫條件γ2(t)+γ3(t)≥0 以及γ1(t)+γ3(t)≥0 能簡化為

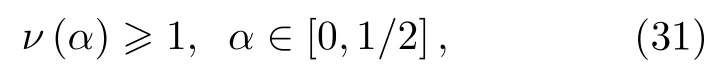
其中,定義ν(α)=2(1-α)p0(t)+2α.文獻[40]給出了在這種特殊情況下基于跡距離和映射的可分性的馬爾科夫條件為

其中,定義μ(α)=4αp0(t)+2(1-2α)和Q(α)=2p0(t)α(1-α)+2(1-α)2.一般來說,方程(31)-(33)所示的馬爾科夫條件是不同的,但在某些具體參數α下也有相同的情況.表1 列出了幾種流行的非馬爾科夫度量對不同的α值的馬爾科夫條件的比較情況.

表1 中基于量子互熵和量子Fisher 矩陣的馬爾科夫條件的數據已經在文獻[26]中給出.

表1 幾種流行的非馬爾科夫度量對不同 α 值的馬爾科夫條件比較Table 1.Comparisons of the Markovian conditions for some popular non-Markovian measures under different α.

從表1 不難看出3 個有用的信息: 1)當選擇α=1/3 時,表格中的五種非馬爾科夫度量對應的馬爾科夫條件都是相同的;2)當選擇α=1/4 時,除了量子互信息外的其他四種非馬爾科夫度量對應的馬爾科夫條件也都是相同的,且與其他度量相比,基于量子互信息對應的馬爾科夫條件是更廣一些;3)當選擇α=2/5 時,這五種非馬爾科夫度量對應的馬爾科夫條件則是完全不同的,且與其他度量相比,基于量子Fisher 信息對應的馬爾科夫條件更廣一些.特別地,與量子Fisher 信息矩陣相比,基于量子Fisher 信息對應的馬爾科夫條件也是更廣一些.另外也注意到,雖然量子Fisher 信息與量子相對熵相干性[49]是兩個完全不同的物理量,且表達式也不同,但當選擇α=2/5 時,基于量子Fisher 信息對應的馬爾科夫條件p0(t)≥0.167 同利用量子相對熵相干性給出的條件[40]是相同的.其原因可能是在考慮具體的通道參數(如p1(t)=p2(t)=α(1-p0(t)))導致γ1(t)=γ2(t).因此,對于隨機幺正通道各種非馬爾科夫度量給出的馬爾科夫條件是否等價與通道的參數密切相關.

另外也注意到,對于相同的隨機幺正通道模型基于量子Fisher 信息的馬爾科夫條件,如γ2(t)+γ3(t)≥0和γ1(t)+γ3(t)≥0,同我們之前的工作[28]中利用量子l1范數相干性給出的馬爾科夫條件是相同的.這是否暗示著量子 Fisher信息和量子態的量子l1范數相干性之間存在某種密切的聯系? 通過直接計算不難發現: 不管是隨機幺正通道還是零溫度振幅耗散通道和相位衰減通道模型,相位參數的量子Fisher 信息都恰好等于系統演化態中的量子l1范數相干性的平方,即F(ρ(θ))=,其中是著名的量子l1范數相干性[49].注意到,對于單個兩能級系統,在一般的參數化背景下也存在一個類似的關系[50].然而,這里需要說明的是,這個關系可能只對二能級系統是適用的,對多維系統是不成立的.其原因是: 在多維系統的量子態上作參數化處理時,可能不是所有的非對角元都帶參數信息,而二能級系統只有一個非對角元且參數信息恰好在非對角元上,從而導致它是一個特殊情況.如預期的一樣,當選擇γ1(t)=γ2(t)=0時,隨機幺正通道的非馬爾科夫條件簡化成相位衰減通道對應的條件.另外,通過簡單的計算不難發現: 一種特殊的非馬爾科夫過程,即所謂永久的非馬爾科夫過程(eternal non-Markovian process[35],其各種通道的衰減系數滿足γ1(t)=γ2(t)=1/2,γ3(t)=-tanht/2)不能用量子Fisher 信息流來判定其非馬爾科夫過程的發生.因為考慮到γ1(t)+γ3(t)=γ2(t)+γ3(t)=(1-tanht)/2＞0,這樣導致χ(t)總會小于零.其實,這是利用一些量子信息度量在跡保守且完全正定映射下具有非增性的性質來量化開放系統中的非馬爾科夫效應時的局限之一.例如著名的跡距離、量子糾纏、量子互熵和量子Fisher 信息矩陣等都有類似的局限性[35].綜合以上三個典型的非馬爾科夫衰減通道的研究結果看,同跡距離一樣,基于量子Fisher 信息的非馬爾科夫度量可能也是一種與系統初態無關的度量方式,這對文獻[18]中的結果是一個重要的補充.量子Fisher 信息的這個優點是否適用于其他非馬爾可夫模型,還待于進一步研究,但我們認為它至少對于單個兩能級系統經歷單個衰減通道作用模型是成立的.當然,基于量子Fisher 信息的非馬爾科夫度量也有其自身的局限性,如一個系統初始態如果不帶量子Fisher 信息,那么該系統與環境相互作用時,信息依然會在系統與環境之間不斷進行交換,顯然,量子Fisher 信息就不能用來見證非馬爾科夫過程.總之,各種非馬爾科夫度量對于單個耗散通道情況中馬爾科夫或非馬爾科夫效應的量化都能給出彼此等價的條件.然而,它們在量化多個通道,如隨機幺正通道時則給出不完全等價的馬爾科夫或非馬爾科夫條件,這也是人們持續關注非馬爾科夫過程度量問題的興趣所在.

4 結論

本文對于單個開放的兩能級系統,已經將基于量子Fisher 信息的非馬爾科夫度量由系統初態為純態的情況推廣到系統初態為任意態的情況.具體地,通過三種典型的耗散通道模型驗證了這一有用的結果.在探索開放系統中的非馬爾科夫機制時,尋找一種與系統初態選擇無關的非馬爾科夫測度方式不管在理論研究還是實驗角度看都是非常有用的.一方面是只需要關注系統受到外界環境的影響而不需要關心系統自身的量子態;另一方面,它也降低了在實驗上驗證開放系統中非馬爾科夫效應時對于系統初態制備的要求,簡化了實驗的操作性.總之,本文的結果完善了用量子Fisher 信息來檢測開放系統中非馬爾科夫效應的應用范圍,可能在開放系統中的非馬爾科夫機制研究上有一定的理論指導意義.在本文結束之前,有必要對開放量子系統中非馬爾科夫過程發生的物理機制作一個簡要的說明.通常地,開放量子系統中的非馬爾科夫過程基本都是用從系統流向環境的信息在某些時間段會流回系統來解釋[14],也就是說信息的存儲要么處于開放系統中,要么處于環境中.有趣的是,文獻[51]提出了一個不同的觀點,即量子Fisher信息并不僅僅是存儲在系統和環境里,它還可以存在于系統和環境的關聯之中.這個新穎的觀點可能給開放量子系統中的非馬爾科夫過程提供一個更為準確的物理解釋,但目前還沒有一個統一的結論,這留給我們今后進一步深入研究.