以CPI指數和GDP平減指數衡量貨幣供給量對英國通貨膨脹的影響

林汝星

(謝菲爾德大學 經濟學院，英國 謝菲爾德 S10 2TN)

1 研究意義和目的

全球通脹日益嚴重，各國政府相繼采取控制貨幣供給量的緊縮性貨幣政策，以抑制價格水平上升，達到穩定有效地治理通貨膨脹的目的。因此，為了準確有效地衡量貨幣供給量與通貨膨脹率之間長期和短期相關性，理論分析和實證檢驗都是必要的。

在經濟領域，關于通貨膨脹的原因和性質以及相應的政策已經形成了比較完整和系統的理論，大致有兩種觀點：相關性是存在的和相關性是值得懷疑的。筆者查找了相關文獻研究，認為兩者分歧的主要原因是不同的樣本區間和不同的建模方法。總體而言，貨幣供給量是長期影響通貨膨脹的主要原因。因此，筆者嘗試探究以CPI指數和GDP平減指數衡量的貨幣供給量對英國通貨膨脹的影響。

2 研究方法

2.1 數據選擇

選取英國貨幣供給量(M4)、英國消費者價格指數(UKCPI)和英國GDP平減指數(UKGDP)的季度數據，從1970年第一季度到2020年第四季度，記為1970q1到2020q4。

英國CPI指數和GDP平減指數數據來自圣路易斯聯邦儲備銀行(Federal Reserve Bank of St. Louis)，基準年價格水平為2015年。M4的數據來自英格蘭銀行(Bank of England，BoE)。

本文分別對三個變量的自然對數進行取值，以減輕波動幅度造成的影響并消除時間序列數據中的異方差，從而得到三個時間序列：LM4、LUKGDP和LUKCPI。

2.2 模型選擇

(1)

通貨膨脹和價格水平是穩定的，只有貨幣供給量可以長期影響通貨膨脹，因為它比其他變量更直接地影響價格水平。

(2)

貨幣供求平衡時，均衡價格水平由外生貨幣供給量決定，即由中央銀行控制。因此，在M增長率固定的長期均衡狀態下，i是固定的：

(3)

其中，π是通貨膨脹率，ηY是貨幣供給量的彈性。由于ηY的存在，貨幣供給量的增加將被部分吸收，而超出的部分便會引起通貨膨脹。

M4的增加伴隨通貨膨脹率的上升，但當經濟遇到沖擊時，GDP平減指數的增長率比CPI指數的增長率呈現更大波動。2020年，COVID-19疫情席卷全球，英國GDP下降11.3%，GDP平減指數的增長率迅速波動了1%左右，而英國CPI指數的增長率則一直較為平穩。值得注意的是，LUKCPI和LM4的波動速度幾乎相同。因此，可以認為LUKCPI對LM4的變化更敏感，M4和CPI指數之間更可能存在長期和短期均衡關系。

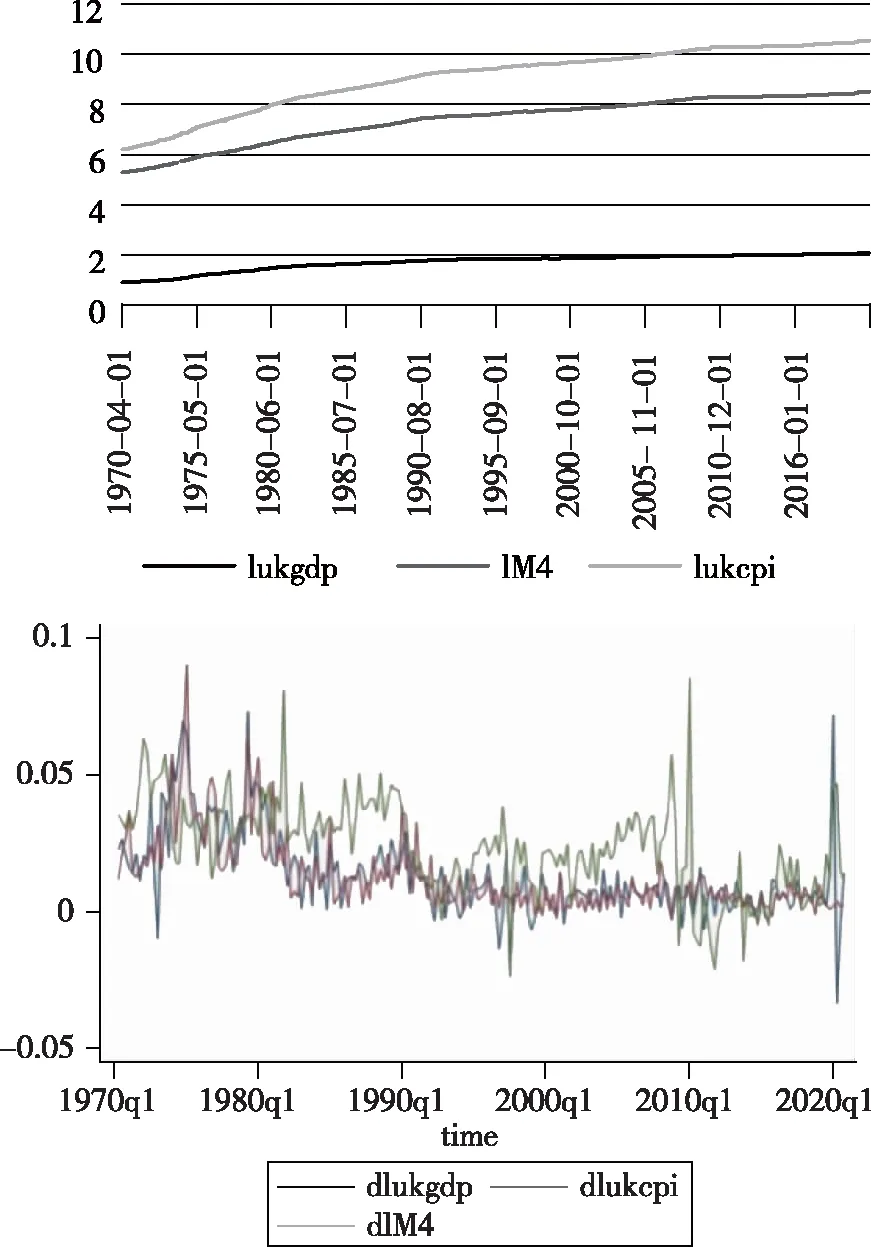
圖1 1970—2020年LM4、LUKGDP和LUKCPI的變化及增長率的波動性

(4)

(5)

其中，Yt代表通貨膨脹，Xt代表貨幣供給量。β1i和γ1i捕捉ΔYt相對于ΔYt-1和ΔXt-1的短期動態，μ1t是白噪聲誤差項。α1和α2反映了對協整關系值的調整速度。本文VECM模型被估計為一個VAR模型，使用OLS估計長期關系Yt=θXt+εt。

(6)

(7)

VAR(q)模型的一般方程如下，A0是截距系數；Ai是自回歸系數；Et是誤差項。

Xt=A0+A1Xt-1+A2Xt-2+A3Xt-3+…+ApXt-p+Et

(8)

3 研究過程

3.1 平穩性檢驗

本文使用Stata軟件分別對三個時間序列進行平穩性檢驗(ADF檢驗)：描述自然波動的平均值(LM4、LUKGDP和LUKCPI)，描述自然波動增長率的一階差分序列(DLM4、DLUKGDP和DLUKCPI)，以及描述增長速度的二階差分序列(D2LM4、D2LUKGDP和D2LUKCPI)。

表1 ADF檢驗結果

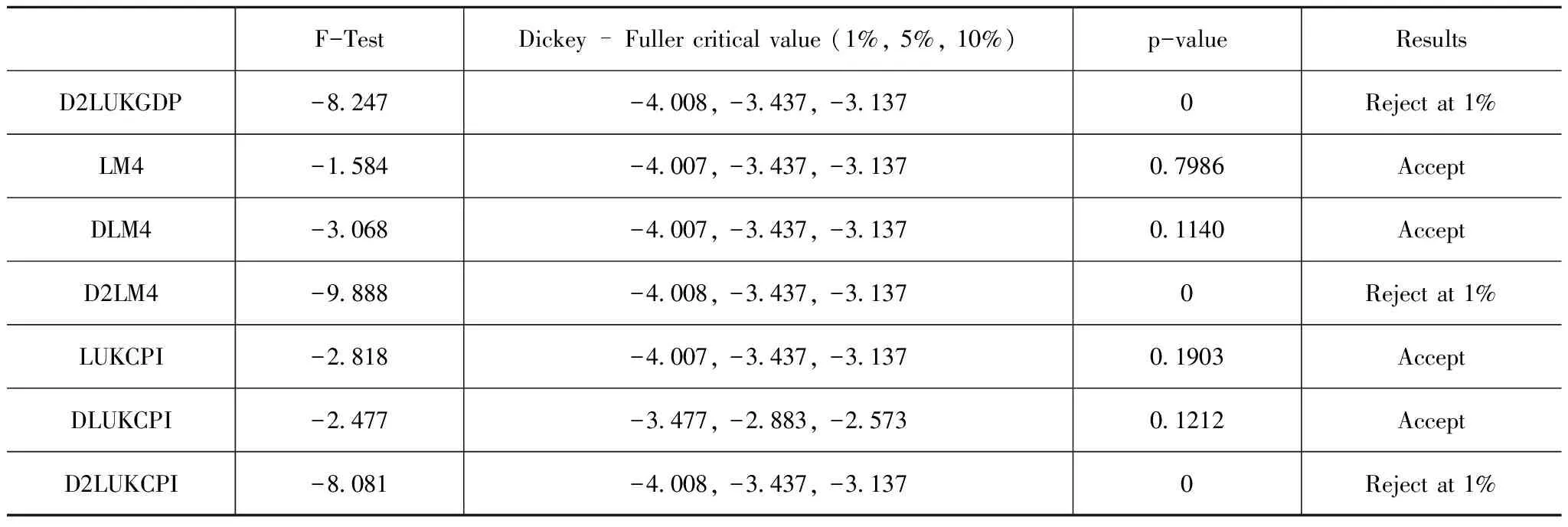
續表

從表1可以得出，平均值時間序列以及一階差分時間序列都不平穩，而二階差分時間序列是平穩的。因此， LM4、LUKGDP和LUKCPI都是I(2)時間序列。

3.2 Johansen協整檢驗

3.2.1 LUKGDP和LM4之間的協整關系

根據滯后項長度分析決定使用VAR(6)和VAR(2)模型，因VAR(2)模型在跟蹤檢驗和最大特征值檢驗中表現不顯著，最終選擇VAR(6)模型。

表2 LUKGDP和LM4的協整檢驗方程

從表2可以得出：

-LUKGDP+26.1789LM4-393.4015=0

(9)

LUKGDP=26.1789LM4-393.4015

(10)

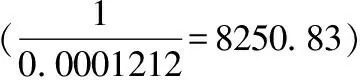
3.2.2 LUKCPI和LM4之間的協整關系

重復滯后期長度分析決定VAR(6)模型的選擇，并且VAR(6)模型在跟蹤檢驗和最大特征值檢驗中表現顯著。

表3 LUKCPI和LM4的協整檢驗方程

從表3可以得出：

-LUKCPI+23.7634LM4-353.3308=0

(11)

LUKCPI=23.7634LM4-353.3308

(12)

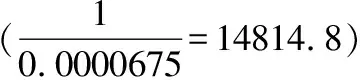
3.2.3 LUKCPI、LM4和LUKCPI之間的協整關系

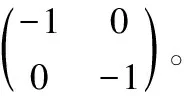
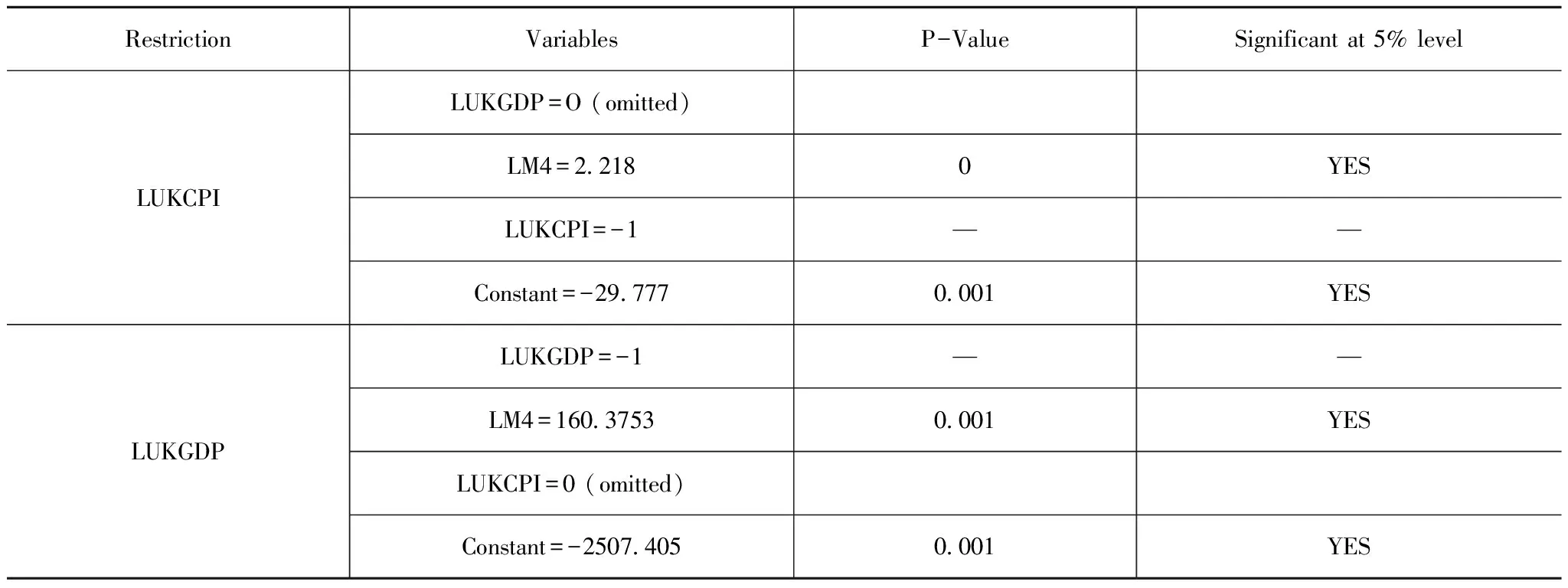
表4 LUKGDP、LM4和LUKCPI的協整檢驗方程

從表4可以得出：

-LUKCPI+2.218LM4-29.777=0

(13)

LUKCPI=2.218LM4-29.777

(14)

-LUKGDP+160.3753LM4-2507.405=0(15)

LUKGDP=160.3753LM4-2507.405

(16)

方程(14)中M4系數相對接近于1，這與相關經濟理論結果一致。方程(16)中M4系數和常數值都很大，單位M4變化，GDP平減指數都有巨大差異和明顯波動，在預測通貨膨脹方面表現不佳。與之相比，CPI指數變化相對不受M4波動的影響。LUKCPI的調整速度參數為0.0099181，與LUKCPI的系數符號相反，表明單位時間LUKCPI的偏差將增加0.0099181。LUKGDP的調整速度參數為-0.0001211，符號與LUKGDP的系數相同，表明單位時間LUKGDP的偏差將減少0.0001211，低于CPI指數，即GDP平減指數對歷史波動的反應不如CPI指數。換言之，CPI指數的波動趨勢與M4的波動趨勢更為相似，即CPI指數更加敏感和有效。

3.3 格蘭杰因果檢驗

格蘭杰因果關系被用來檢驗每個變量是否改善了另一個變量的預測，即該變量對其他變量的未來價值的預測能力。

表5 VAR(6)模型的格蘭杰因果關系Wald檢驗

結果表明，M4的變化不是CPI指數和GDP平減指數的格蘭杰原因，考慮M4歷史值的基礎上，M4變化的歷史值不能改善對CPI指數和GDP平減指數的預測。然而，CPI指數和GDP平減指數都是M4變化的格蘭杰原因，概率分別為96.5%和91.7%。綜上所述，M4變化對引起CPI指數變化更明顯也更敏感，更適用于預測通貨膨脹。

3.4 SVAR模型和脈沖響應函數

在相關經濟理論基礎上，對上述VAR(6)模型施加進一步限制條件，生成結構性VAR(SVAR)模型來進一步識別LM4、LUKCPI和LUKGDP之間的因果關系。結果顯示，GDP平減指數的R2=0.7456，而CPI指數的R2=0.8314，表明CPI指數在模型擬合程度上更優。

由于沒有理論依據認為M4會受到GDP平減指數和CPI指數的同期影響。此外，GDP平減指數和CPI指數并不同時受到對方的影響，設定b12=b32=b13=b31=0。

(17)

因此，M4方程可以寫成：

-0.2826LUKGDP+LM4+0.486LUKCPI=0

(18)

LM4=0.2826LUKGDP-0.486LUKCPI

(19)

為分析GDP平減指數和CPI指數如何應對M4的一次性正向沖擊，生成脈沖響應函數，其中LM4是脈沖變量，LUKGDP和LUKCPI是響應變量。

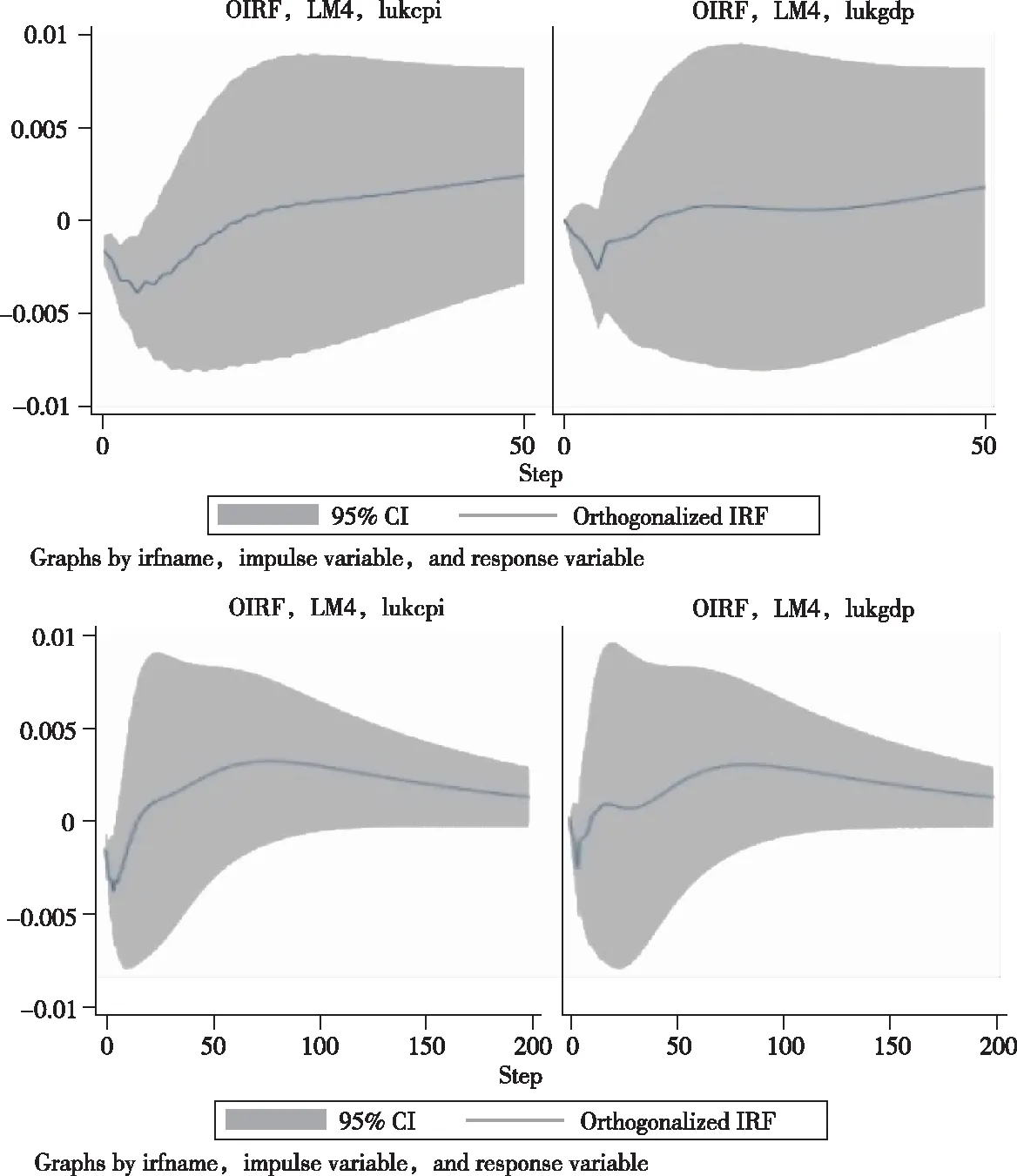
圖2 50和200個季度的脈沖響應函數

從圖2可以看出，CPI指數對M4沖擊的反應從零季度開始下降并達到最低點。自第五季度，反應上升并逐漸趨于穩定。初始階段，M4對GDP平減指數沖擊反應趨近于零。但在后續十個季度，沖擊影響急劇增漲并達到頂峰。總體來說，M4沖擊對CPI指數有顯著而長期的影響，而對GDP平減指數則是短期波動更為明顯。因此，M4是長期調整CPI價格水平的一個更有效的變量，能夠更有效地預測通貨膨脹。

4 結論與建議

貨幣供給量和通貨膨脹之間既存在短期波動效應，又存在長期均衡分布。從長期來看，貨幣供給量的增加與通貨膨脹之間存在顯著的正向協整關系。由于外部沖擊，短期波動顯著。如果貨幣供給量迅速增加，GDP平減指數的波動將超過CPI指數。因此，如果GDP的某個組成在短期內迅速上升，卻沒有引起價格水平變化時，GDP平減指數的波動將大于CPI指數，此時利用GDP平減指數預測通貨膨脹可能會高估通貨膨脹水平。除此之外，貨幣供給量的增加不能歸因于通貨膨脹率的上升，即通貨膨脹率的上升或下降，并不會引起貨幣供給量的變化。

在實踐中，應考慮結合使用CPI指數和GDP平減指數來更有效準確地衡量和預測通貨膨脹水平。但是，GDP平減指數只能按年度或季度計算，不能及時反映價格波動，使其不適合用于短期波動預測。

在撰寫本報告時，英國CPI通脹率(2021年第二季度)為3.2%，存在著持續高通脹的風險，促使英國央行實行更緊縮的貨幣政策。本文研究表明，監測貨幣供給量的變化并在短期內收緊貨幣政策可以幫助英國央行將通脹率帶回目標。然而，本文是基于經濟穩定的假設，沒有考慮英國脫歐帶來的影響，所以本文的結論并不完全適用于現階段和未來英國通脹分析。

本文可以在以下三個方向上進行擴展。首先，雖然模型重點是英國通脹動態，但該模型對其他國家亦有借鑒性。其次，本文結果表明將英國的通貨膨脹建模為經濟政策不確定性函數模型是合理的，以有效反映英國脫歐影響和未來發展。最后，非線性模型在樣本外預測通脹的能力是具有探究性的，需要未來更深入的探究。