基于拉普拉斯修正公式的服裝壓力分析

侯欽華，陳郁

(上海工程技術大學 紡織服裝學院，上海 201620)

壓力療法又稱加壓療法，是指通過對人體體表施加適當的壓力，以預防或抑制皮膚瘢痕增生、防治肢體腫脹的方法[1]。服裝壓的確定是加壓療法的重點，也是近年來的研究熱點。

目前，服裝壓分布的研究方法主要包括理論預測法、數值模擬法、折減系數法、實驗法等[2-3]，其中基于拉普拉斯公式計算壓力的理論預測法是常用方法之一。拉普拉斯公式最初是用以描述液體表面張力、液體曲率與薄膜壓力之間關系的,CHENG J C Y等[4]發現服裝壓與人體尺寸也可用此公式解釋，于是拉普拉斯公式開始應用于服裝領域。

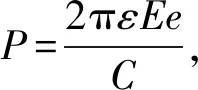
實際上，人體同一橫截面上各部位的曲率并不均勻[10]，以手臂為例，手臂橫截面的形狀更接近于橢圓形[11]。理論上，橢圓長軸部位曲率半徑小，服裝壓大，短軸則相反。對于人體某些點狀或者小面積的患處，只計算平均壓力很難達到所需壓力的要求。文中以手臂為研究對象，假設手臂橫截面為橢圓形，在此基礎上對拉普拉斯公式進行修正，并通過實驗驗證修正公式的有效性。

1 理論推導

1.1 手臂模型建立

由于手臂的橫截面更接近于橢圓，文中將手臂橫截面假設為橢圓形剛體，具體如圖1所示。由圖1可以看出，以手肘處截面中心O為原點，手臂軸線為x軸，則截面橢圓半長軸和半短軸是x的函數。手臂微元如圖 2所示。對于x到x+ dx處的截面圍成的微元，可看成以x處的橢圓截面為底，高為 dx的橢圓圓柱。

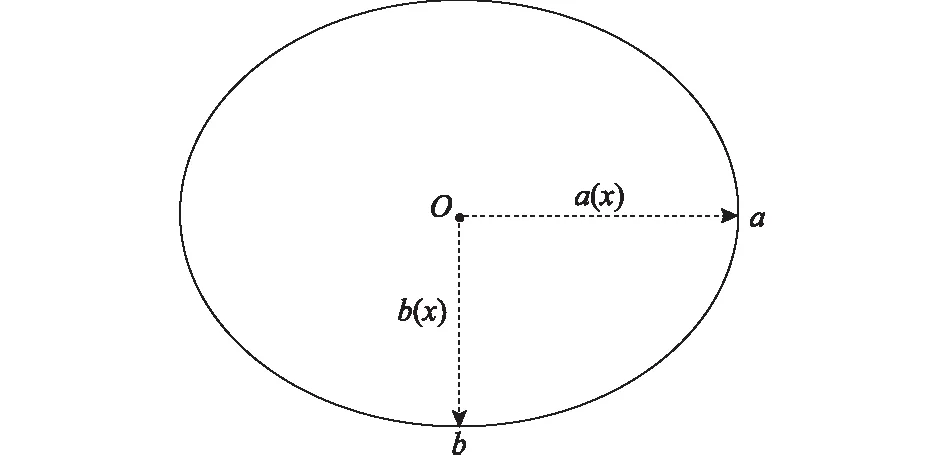
圖1 手臂橫截面Fig.1 Arm cross section

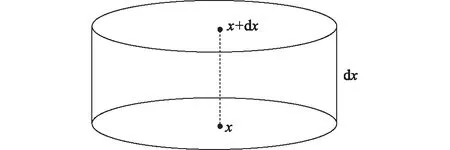
圖2 手臂微元Fig.2 Arm micro element

將面料剪成長為2πr、寬為h的長方形，并將寬邊接合，圍成半徑為r、高為h的圓柱形臂套。

1.2 模型求解

把圓柱形臂套穿戴在手臂上，臂套面料受到手臂的作用而伸張，伸張后的面料反過來又會對手臂形成一個壓力。

橢圓圓柱滿足拉普拉斯方程

(1)

式中:p為壓強(Pa);T為面料縱向張力系數，即面料單位長度的拉伸力(N/mm)；R為人體曲率半徑(mm)。

面料是由多股紗線構成，因此以一股紗線的形狀作為其基本單元，具體如圖3所示。圖3中紗線直徑為D，假設直徑即為面料厚度。

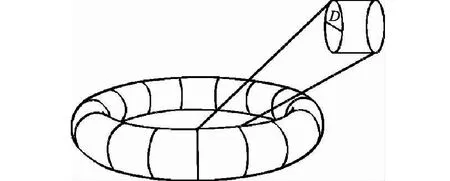
圖3 面料基本單元Fig.3 Fabric basic unit

假設求得一股紗線受到的力為F，則張力系數

(2)

在面料由圓柱變形為橢圓柱時，紗線由圓變為橢圓。假設該變形為彈性形變，在紗線上取一小段作為微元，假設在壓力F的作用下發生彈性形變，長度由dl變為dl′，截面積由S變為S′，直徑由D變為D′，則微元上的正應力

σ=Eε，

(3)

式中：E為面料彈性模量；線應變

于是微元處的張力系數

(4)

由于紗線的體積不變，則

Sdl=S′dl′ 。

(5)

紗線由圓變形為橢圓的始末狀態如圖4所示。

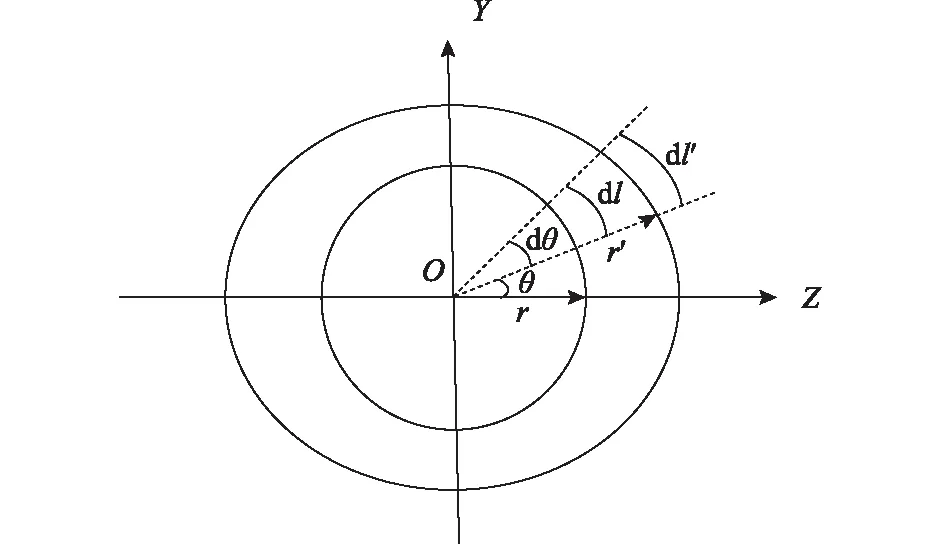
圖4 穿戴在手臂上的臂套面料變形始末狀態Fig.4 State of cloth deformation worn on the arm

圖4中，dl=rdθ，取水平方向為Z軸，豎直方向為Y軸，θ為r′與OZ軸的夾角。

又S正比于D2，故

rD2=r′D′2。

(6)

將式(6)代入式(4)，得

(7)

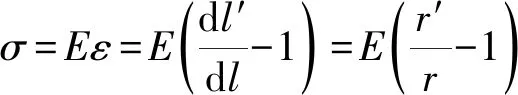
(8)

橢圓的周長公式[12]

(9)

其中

(10)

橢圓的曲率半徑

(11)

橢圓參數方程為

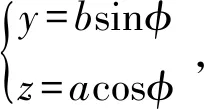
(12)

故

(13)

因此曲率半徑可表示為

(14)

最后將式(8)和式(14)代入式(1)，求得

(15)

由此可知，當手臂給定，即a,b給定時，臂套給予手臂的壓力與面料的彈性模量E、構成面料的紗線直徑D以及臂套半徑r有關。

2 材料與方法

2.1 原料與儀器

2.1.1原料 選取市面上常用的3種壓力服氨綸面料，均購于上海懿臣有限公司。面料規格見表1。

表1 面料規格

2.1.2儀器 YG026D型多功能電子織物強力機、YG141數字式織物厚度儀，均由寧波紡織儀器廠制造；AMI3037-10氣囊式壓力傳感器，北京力泰友聯科技有限公司制造。

2.2 面料參數測試

2.2.1面料拉伸力 參照FZ/T70006—2004《針織物拉伸彈性回復率試驗方法》[13]，將面料裁剪為150 mm×50 mm的試樣，采用定伸長的拉伸方法，使用多功能電子織物強力機測其拉伸力，每組實驗做3次，取平均值。采用彈性模量公式計算出面料的彈性模量E，即

(16)

式中：σ為應力(kPa)；ε為應變；F為拉伸力(N)；l為面料的長度(mm)；S為面料的橫截面積(mm2)；Δl為面料的伸長量(mm)。

2.2.1面料厚度 采用數字式織物厚度儀分別測量3種面料的厚度。面料的彈性模量和厚度見表2。

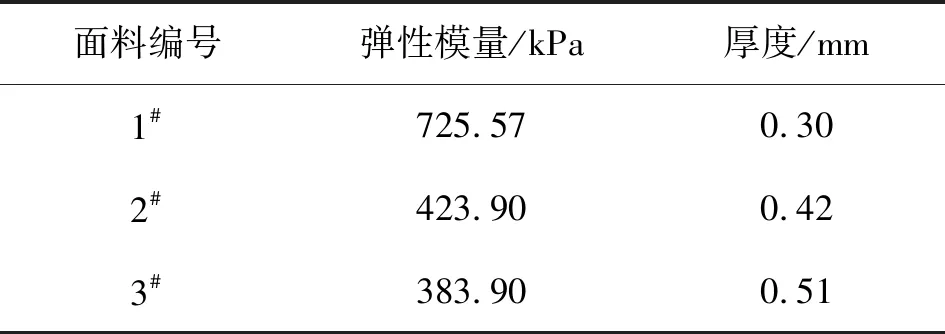
表2 面料彈性模量和厚度

2.3 壓力臂套的制作

2.3.1臂套圍度的確定 選取20名年齡(22±2)周歲，身高(160±3) cm，體質量(50±3) kg的成年女性為受試者，令其保持手臂展開45°的站姿，使用三維人體掃描儀掃描手臂，結果如圖5所示。將掃描得到的點云數據導入Geomagic軟件中進行處理，以腕關節向上1 cm為手腕處圍度，再向上15 cm為手肘處圍度，測得所需圍度數據，并計算平均值。

圖5 手臂掃描結果Fig.5 Arm size measurement

設置不同的壓縮系數(15%，20%，25%，30%)，經計算確定臂套圍度。具體結果見表3。

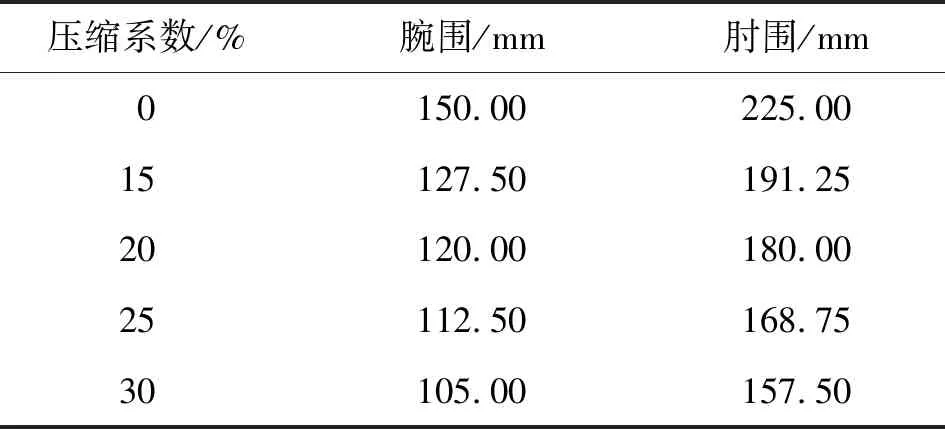
表3 臂套圍度

2.3.2臂套縫制 根據表3數據對臂套進行打版，裁剪面料，采用鎖邊縫的方法縫制臂套，得到4種不同規格的臂套，具體如圖6所示。

圖6 不同壓縮系數的臂套成品Fig.6 Sleeve finished products

2.4 壓力測試

2.4.1受試者的確定 在20名受試者中任選5名受試者進行壓力測試。

2.4.2壓力測試點的確定 為了不受腕骨凸的影響，選取腕關節凸起最高處以上3 cm為測量位置，每一圍度測4個點，具體測量部位如圖7所示。

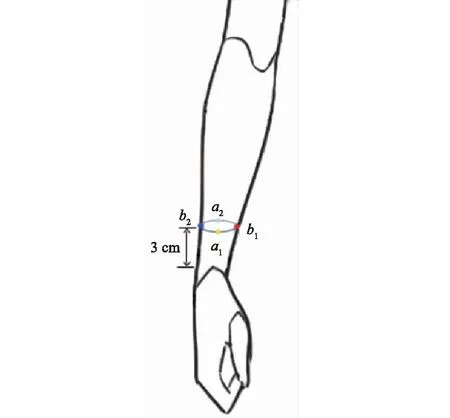
圖7 測量位置與測量點Fig.7 Measuring position and measuring point

首先采用三維掃描儀掃描5名受試者手臂，將掃描得到的點云數據導入Geomagic軟件，再使用軟件對圖像進行標記測量，測出手腕處測量點長軸(a)與短軸(b)半徑，測量結果見表4。

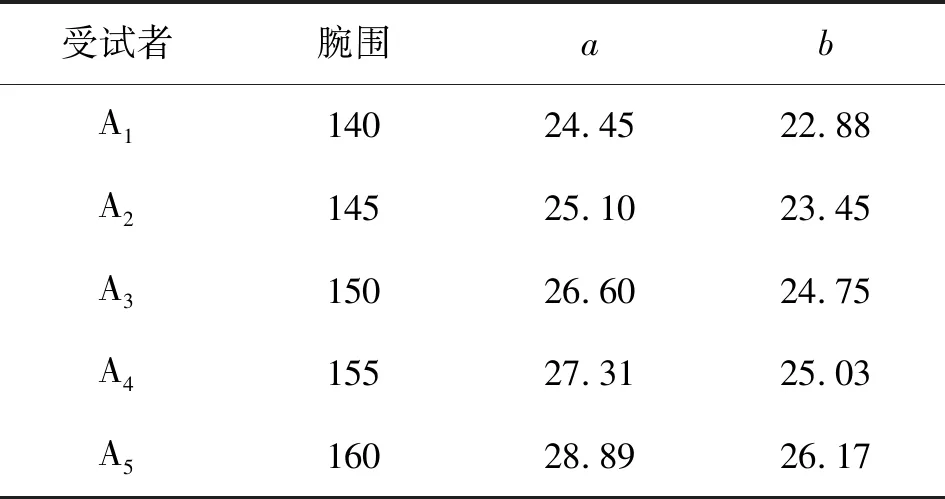
表4 手臂尺寸

2.4.3壓力測試 使用氣囊式壓力傳感器，對受試者手臂部位進行壓力測量。每個臂套測量3次，取平均值。測量結果見表5。

由表5可以看出，隨著受試者腕圍的增大，手臂受到的壓力逐漸增大；對于同一受試者，臂套壓縮系數越大，手臂所受壓力越大；同一受試者在相同壓縮系數條件下，手臂a點的壓力值大于b點的壓力值，這驗證了手臂曲率越大所受壓力越小的理論。

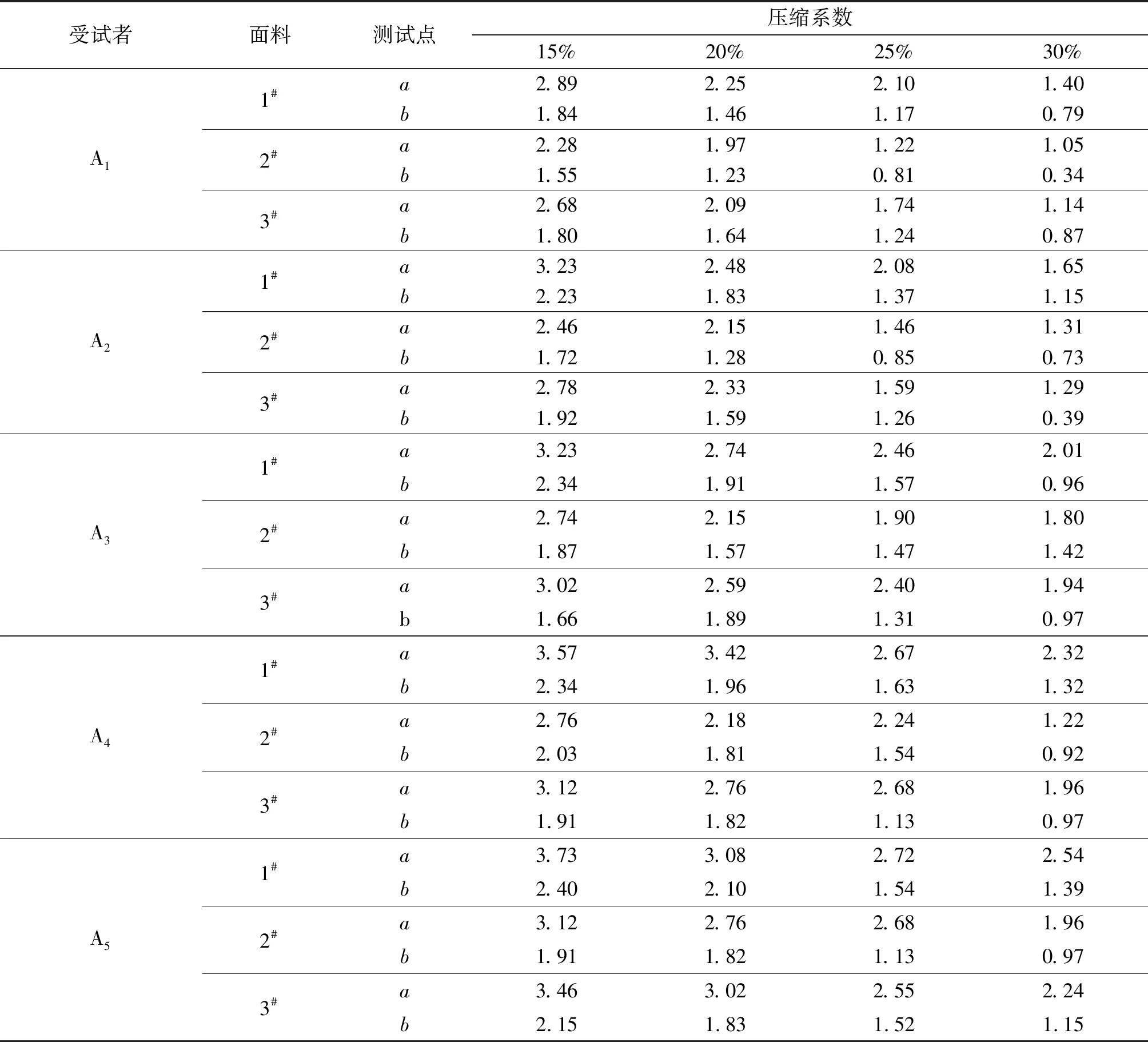
表5 實測壓力

3 分析與結果

3.1 理論計算與數據分析

在Maple軟件中，將A3受試者和2#面料的數據代入公式，使用軟件的繪圖功能，得到手臂部位、臂套尺寸與壓力之間的關系，具體如圖8所示。其中R為壓力臂套的半徑；φ為手臂圍度測量點對應的位置；p為各位置對應的壓力。

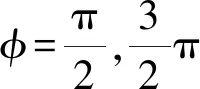
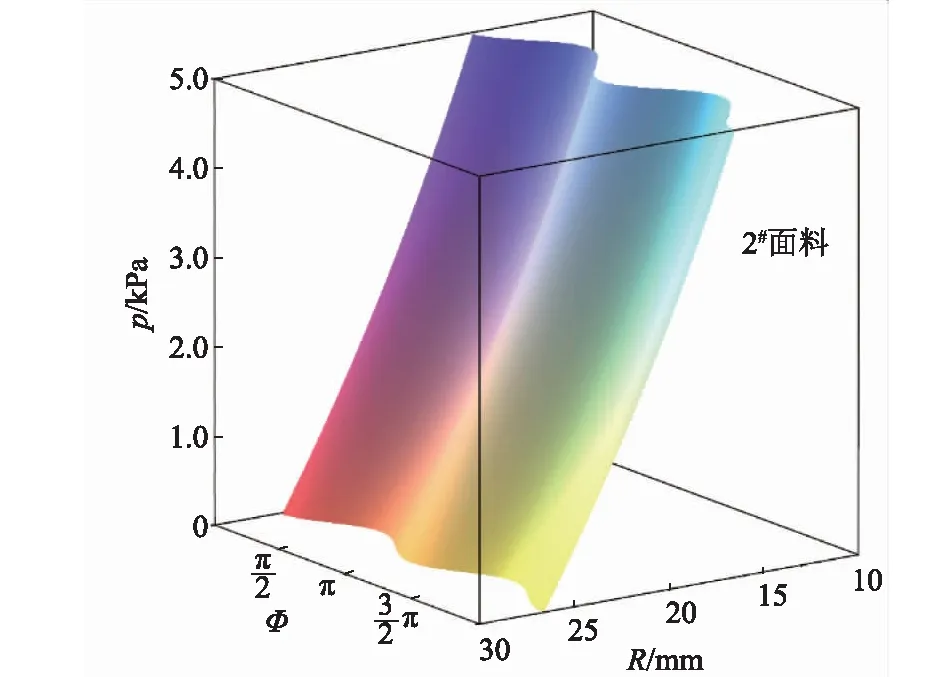
圖8 手腕處臂套半徑R、手臂測量部位φ與壓力p的關系Fig.8 Relationship of arm sleeve radius and arm measuing position with pressure at wrist

將5個受試者手臂尺寸與3種面料參數代入公式，求出理論壓力值(即壓力預測值)，具體見表6。

由表5和表6可以看出，預測壓力與實測壓力有相同的變化趨勢，兩者最大值所對應的均是A5受試者、1#面料的a點，預測壓力最大值為4 kPa，實測壓力最大值為3.73 kPa；兩者最小值所對應的均是A1受試者、2#面料的b點，預測壓力最小值為0.64 kPa，實測壓力最小值為0.34 kPa。由此證明,文中預測模型在整體思路上是正確的，但預測壓力比實測壓力整體偏大，預測模型還需進一步改進。

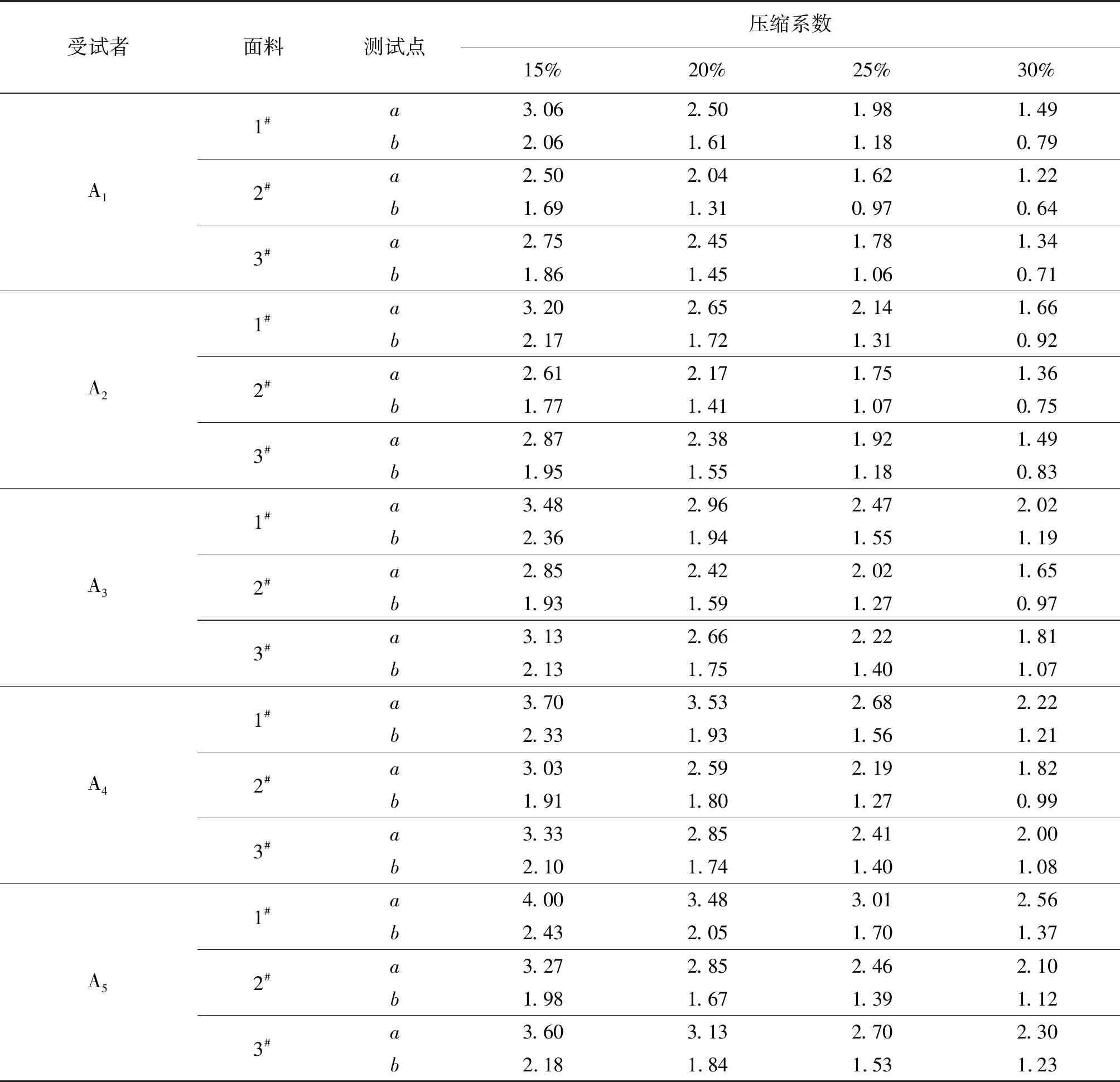
表6 預測壓力

3.2 相關性分析

將預測壓力與實測壓力代入SPSS軟件中進行相關性分析，具體結果見表7。

由表7可以看出，預測壓力接近于實測壓力的平均值，標準差也相近，預測值與實測值相關性系數為0.974，在0.01級別相關性顯著。

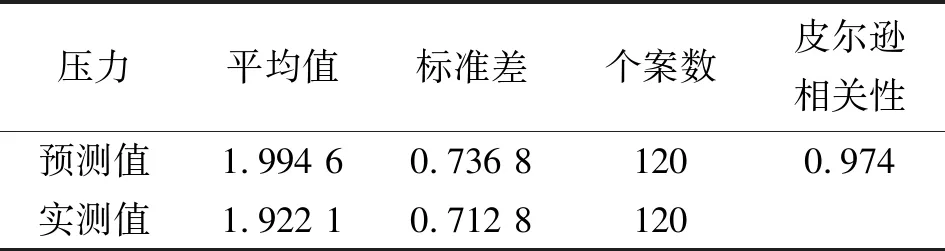
表7 相關性分析

3.3 比較

BARHOUMI H[9]的拉普拉斯修正公式

(17)

式中：pB為預測壓力；ε為面料應變；E為面料彈性模量；e為面料厚度；C為身體圍度。

BARHOUMI公式預測的壓力值比拉普拉斯公式的預測值更為準確，但其所求壓力為截面上各點的平均值，因此a,b兩點的預測值相同。

文中使用誤差率分析預測壓力的準確性，即

(18)

式中：δ為誤差率；pC,PM分別為預測壓力值和實測壓力值。

為了比較文中修正公式與BARHOUMI修正公式預測壓力的準確性，以A3受試者為例，計算穿戴3種不同面料臂套時手臂的實測壓力、預測壓力平均值。兩種修正公式預測準確性的比較結果見表8。

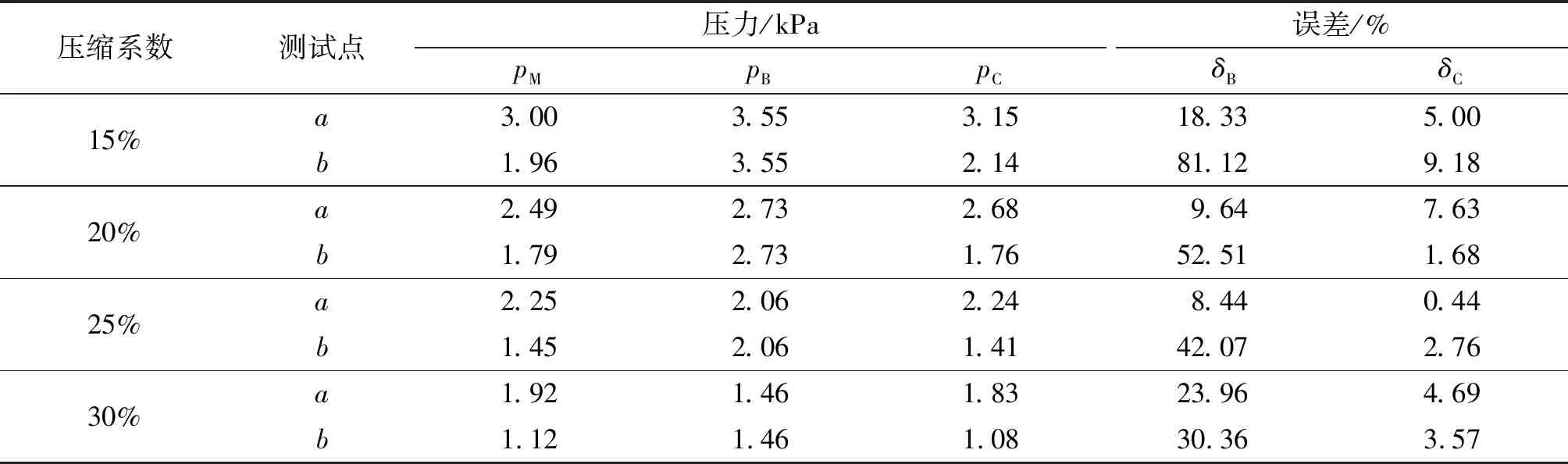
表8 兩種預測方式的預測準確性比較

由表8可以看出,文中修正公式的預測準確性更高。 對于曲率較大的測試點a，BARHOUMI修正公式依然能保持較高的預測準確性，但在曲率較小的b點，BARHOUMI修正公式的預測準確性大大降低。文中修正公式在測試點b的預測準確性雖然比在測試點a的低，但對比其他公式準確性得到了顯著提高，該修正公式為壓力服的定制與精準施壓提供了有力的參考。

4 結語

文中根據建立的手臂橢圓柱模型對拉普拉斯公式進行修正，通過實驗驗證了該公式的準確性，結果表明：

1)由于曲率不同，手臂同一截面各部位的壓力存在較大差異，使用拉普拉斯公式時將手臂截面假設為橢圓形更合理。

2)修正后的拉普拉斯公式包含了面料彈性模量、厚度、橢圓長短軸等參數；基于橢圓截面的拉普拉斯方程計算得到的手臂壓力分布規律與實際壓力分布基本一致，可用于預測手臂截面曲線上的壓力。

3)將橢圓模型拉普拉斯公式BARHOUMI拉普拉斯公式對比，文中公式的預測準確性得到了一定的提高。因此在手臂壓力分布研究與壓力臂套精確定制中，可使用橢圓模型拉普拉斯公式進行計算。