海上風電變徑樁基礎模態(tài)分析

沈曉雷，龔 睿，周茂強，蘇 凱，3，4

(1.浙江華東工程咨詢有限公司，浙江杭州310014；2.武漢大學水資源與水電工程科學國家重點實驗室，湖北武漢430072；3.武漢大學水工巖石力學教育部重點實驗室，湖北武漢430072；4.武漢大學海綿城市建設水系統(tǒng)科學湖北省重點實驗室，湖北武漢430072)

0 引 言

風力發(fā)電作為一種綠色能源，具有環(huán)保、資源豐富、經(jīng)濟效益高等諸多優(yōu)勢，現(xiàn)已成為當今能源發(fā)展浪潮中的領航標。相比于陸上風電，海上風電開發(fā)資源潛力巨大、占地面積小、噪音污染低，更具有開拓性[1]。海上風機可簡化為由基礎、塔架、機艙(含葉輪)三部分構(gòu)成，風機基礎作為整個結(jié)構(gòu)的“根部”，深入海洋與土壤結(jié)合穩(wěn)固，對于結(jié)構(gòu)整體的穩(wěn)定、安全運行至關重要。單樁基礎是目前應用最廣泛的海上風機基礎形式，適用于水深不超過30 m的海域，截至2015年，在歐洲國家海上風機單樁基礎已占到78%[2]。

隨著海上風電逐步向深水域開拓，環(huán)境荷載逐步增大，結(jié)構(gòu)會大幅度晃動，故由此提出了樁身變徑的方法[3]。變徑樁可有效減小風、浪、流荷載的作用面積，對于合適的變徑段位置，其橫向承載力更經(jīng)濟[4]，變徑段的存在使得樁基礎與塔筒的連接更平順，對樁基礎的分析更具有多樣性。但整個風機結(jié)構(gòu)細長高聳，樁基礎段受外源荷載較多，振動特性復雜，特別是在一定頻率下極易發(fā)生共振，嚴重時會導致重大設備事故，而模態(tài)分析可初步得到結(jié)構(gòu)振頻與振型，可預測在外源荷載下的動力響應，故對樁基礎展開模態(tài)分析十分必要。

目前許多學者對樁基礎的模態(tài)分析展開過研究。靳軍偉等[5]在考慮樁土相互作用的基礎上，探討套筒、土體、基礎等一系列參數(shù)對風機樁基礎的模態(tài)影響規(guī)律；李益等[6]比較了m法與p-y法的樁土相互作用對整體結(jié)構(gòu)自振特性的影響；趙密等[7]利用MATLAB對水-樁-土體相互作用的單樁基礎的固有頻率求其解析解，并與有限元結(jié)果進行對比；許成順等[8]探討了水體附加質(zhì)量對大直徑單樁基礎的影響，并在此基礎上對樁、土體、海水等因素進行敏感性分析；王丕光等[9]研究了運行狀態(tài)下基礎水平側(cè)移對海上風機系統(tǒng)自振頻率的影響。

表1 土層物理力學參數(shù)

從以上研究可以看出，目前涉及變徑樁基礎以及針對樁基礎尺寸開展的模態(tài)敏感性分析較少。本文基于ABAQUS有限元軟件，實現(xiàn)交互式參數(shù)化建模過程，利用附加質(zhì)量法來模擬海水，對變徑樁的結(jié)構(gòu)尺寸進行參數(shù)敏感性分析，分析其模態(tài)變化規(guī)律。

1 工程背景與有限元模型建立

1.1 工程背景

本文依托江蘇省南通市如東海域某風機工程項目，風電場涉海面積64 km2，工程規(guī)劃裝機容量400 MW，水深達到15.9 m。海底泥面高程在-18.6～0 m(1 985 m高程)之間，海底地形起伏明顯，部分在理論最低潮面以上。依據(jù)區(qū)域地質(zhì)資料，風電場地基土物理力學性質(zhì)見表1，地層自上而下劃分為7層，⑥-1、⑥-3、⑦-3均為土體持力層[10]。風機采用變徑樁基礎，樁基總長78 m，埋深53.4 m，頂部及底部直徑分別為6、6.5 m，厚度均為70 mm。變徑段總長12 m，其頂部距樁頂21 m。風機塔筒頂部機艙、輪轂、葉片總質(zhì)量為256.86 t。

1.2 有限元模型建立

利用ABAQUS有限元軟件，將坐標原點建立在基礎與海床泥土交界的圓心處，沿風塔高度方位設定為Z軸正方向，海底泥面取為XY面。樁基礎周圍土體尺寸選取長寬為12倍樁徑底部直徑，高為2倍埋深，土體側(cè)面采用法向約束，底面采用全約束。基礎與土體采用實體單元C3D8R，上部塔筒采用殼單元S4R，控制樁基礎與塔筒網(wǎng)格尺寸為0.8 m，土體網(wǎng)格尺寸為1.0 m。土體利用Mohr-Coulomb準則，其與基礎間采用“面面接觸”(surface-to-surface contact)模擬相互作用，將風塔上部葉輪、機艙、輪轂等簡化為集中質(zhì)量點，忽略偏心影響，并與塔筒頂部建立耦合約束，整體有限元模型見圖1。

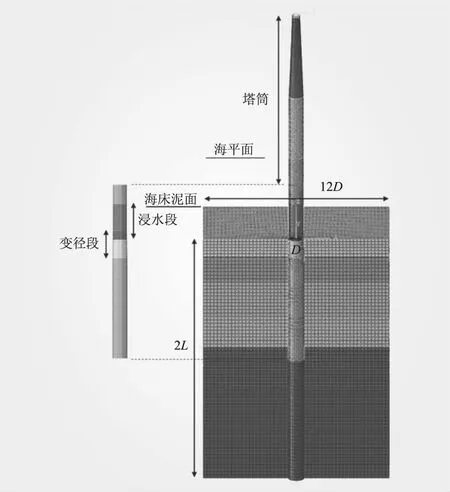
圖1 整體有限元模型示意

本文利用附加質(zhì)量法以模擬樁基周圍水體影響，將附加質(zhì)量的慣性力等效為動水壓力，通過簡化的附加質(zhì)量模型來求解變徑樁在水中的振動響應。假定樁內(nèi)外側(cè)泥面高度、水深基本保持一致[11]，故在分析時要同時考慮內(nèi)外側(cè)水的附加質(zhì)量[12-13]。

對于樁基外側(cè)單位長度附加水質(zhì)量，基于Morison方程，其表達式為

(1)

式中，Dout為樁外徑；ρw為水體密度；Cm為慣性系數(shù)，圓形截面樁取1.0[14]，由于本文考慮樁基為變徑單樁，故此式代表實心樁所排開水體質(zhì)量。

對于樁內(nèi)附加水質(zhì)量，直接以樁內(nèi)部水質(zhì)量代替，其表達式為

Min=ρw·Ain

(2)

式中，Ain為樁內(nèi)部截面積。

本文通過提高水體段樁體有效密度的方式，簡化考慮其內(nèi)外側(cè)附加水體，密度計算公式為

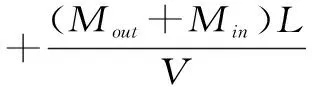
(3)

式中，ρ為浸入水體段樁體密度；ρ鋼為樁基礎鋼材密度；L為樁長；V為浸入水體段樁體體積。

2 模態(tài)分析

基于前文所創(chuàng)建的模型，采用Lanczos法獲得風機結(jié)構(gòu)各階振型與振頻。結(jié)構(gòu)前4階振型如圖2所示，相鄰兩階振型在空間上大致正交，前2階振型呈現(xiàn)擺動形態(tài)，第3、4階開始呈現(xiàn)彎曲形態(tài)。

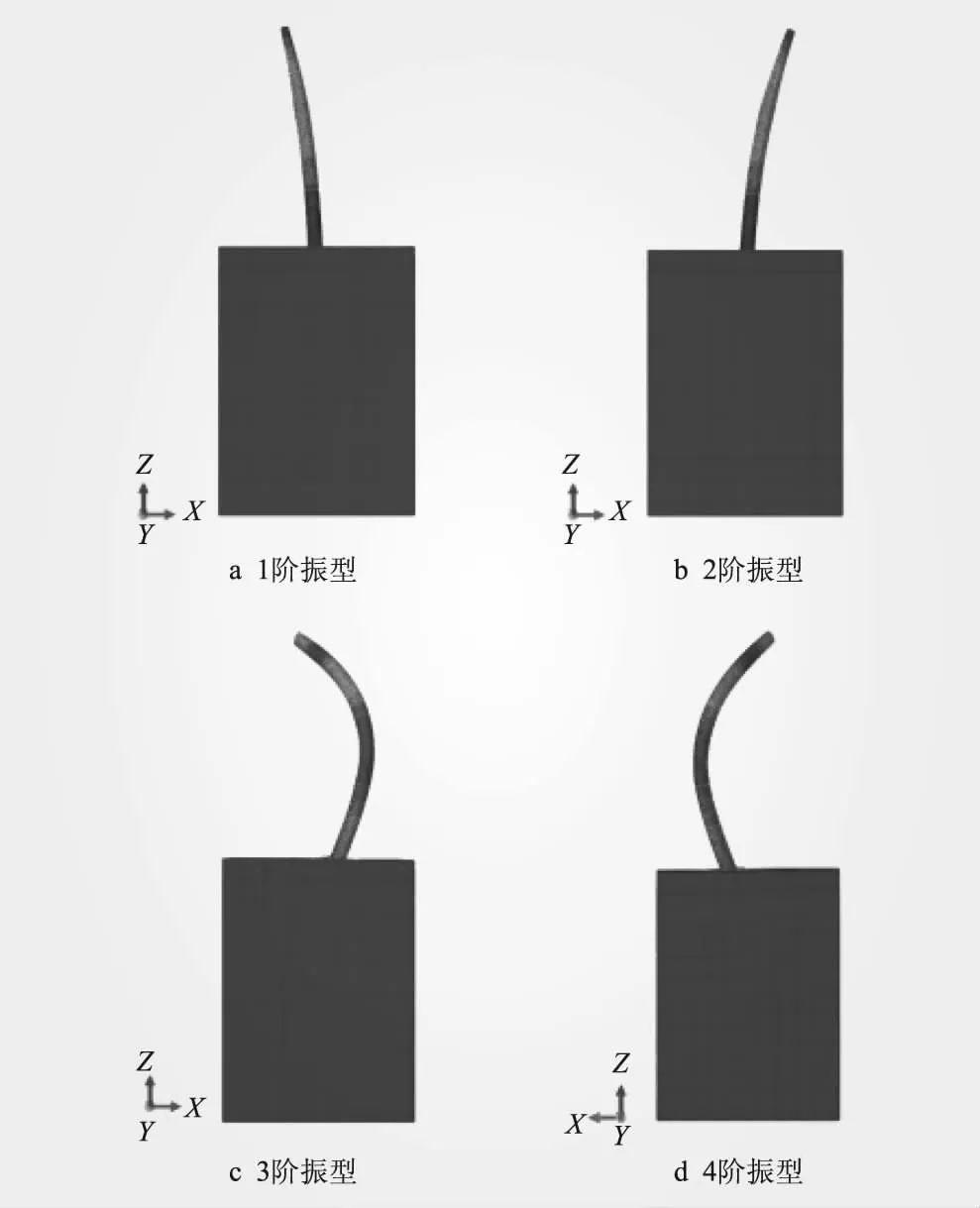
圖2 結(jié)構(gòu)前4階振型

為避免風機結(jié)構(gòu)的機械共振，要求振源的激勵頻率和風機結(jié)構(gòu)的自振頻率有一定的錯開度。頻率錯開度的計算公式為

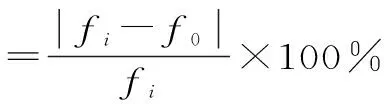
(4)

式中，fi為結(jié)構(gòu)自振頻率；f0為振源的激勵頻率。

本文認為錯開度>20%[15]時可判定無共振可能性。其中振源主要考慮葉輪旋轉(zhuǎn)產(chǎn)生的1P氣動載荷、3P氣動轉(zhuǎn)矩脈動與波浪頻率，項目風機轉(zhuǎn)速范圍為6～12.9 r/min，故1P、3P頻率分別為0.1～0.215、0.3～0.645 Hz，此外，通過查看波浪站全年平均周期分布統(tǒng)計表，得到波浪頻率范圍為0.096～0.135 Hz，錯開度計算結(jié)果見表2。

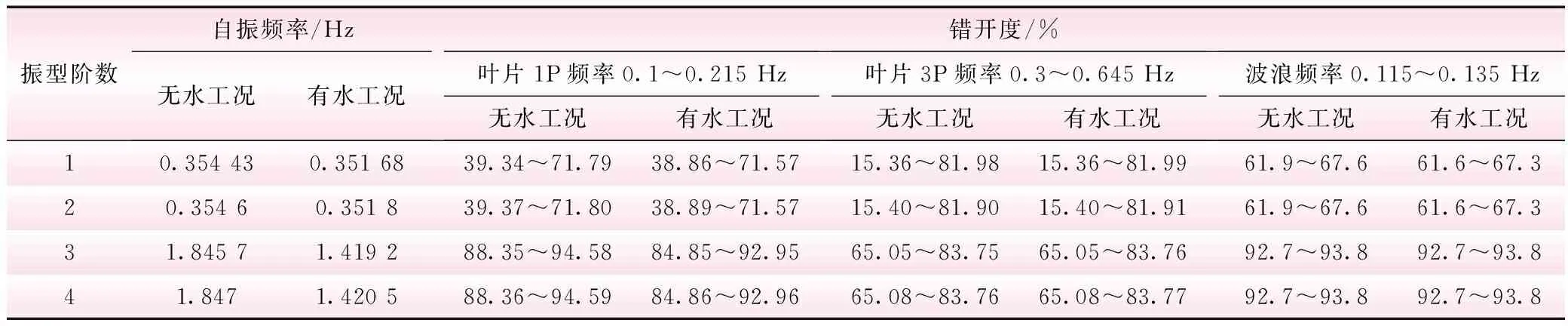
表2 頻率校核結(jié)果

從校核結(jié)果分析可知，風機相鄰兩階振動頻率基本保持一致，結(jié)合振型規(guī)律，這是由于整體結(jié)構(gòu)在空間上是對稱結(jié)構(gòu)。由表2可知，風機的1、2階頻率與葉片3P頻率錯開度值部分小于20%，可能產(chǎn)生共振，但3階及以后各階自振頻率與各振源頻率錯開度值均大于60%，階數(shù)越高越具有良好的錯開度，故在此只展示前4階數(shù)據(jù)。

另一方面，由于泥面以上樁體長度為24.6 m，改變水深條件，由無水至水深20 m，分析水深改變對風機振動頻率的影響。由表2可知，風機前2階頻率是引起共振的主要振頻，且兩者數(shù)值基本保持一致，故只考慮水深對結(jié)構(gòu)基頻的影響，結(jié)果見圖3。由圖3可知，水深增加使得結(jié)構(gòu)基頻逐步下降，更接近振源頻率，錯開度也會相應減小，產(chǎn)生共振的可能性也相應增大。隨著水深的增加，風機基頻下降幅度也逐步增大，而單樁最大支持水深為40 m[16]，故模態(tài)分析時考慮水深影響十分重要。

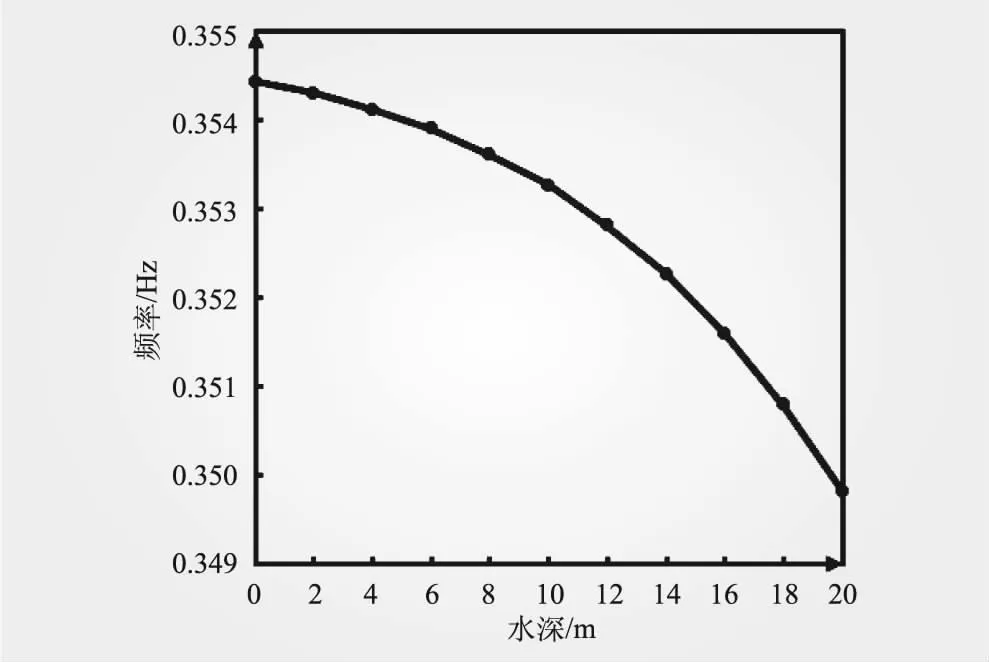
圖3 水深對結(jié)構(gòu)基頻的影響

3 樁基礎參數(shù)敏感性分析

樁基礎作為風機結(jié)構(gòu)的基部，向上與塔筒結(jié)構(gòu)連接，向下與海洋、土壤穩(wěn)固，在整個結(jié)構(gòu)中起著關鍵性作用，并且考慮到研究風機尚存在一定的共振風險，本節(jié)將從樁基礎整體及變徑段結(jié)構(gòu)兩個方面展開討論，考慮因素包括基礎整體樁徑、壁厚、埋深以及變徑段布置參數(shù)，同時需要注意的是，考慮到計算方案的不同，浸入水體樁基內(nèi)外側(cè)附加質(zhì)量也將一并調(diào)整。

3.1 基礎結(jié)構(gòu)影響

分析樁基礎結(jié)構(gòu)樁徑、壁厚與埋深對結(jié)構(gòu)整體自振特性的影響，結(jié)果如圖4所示。

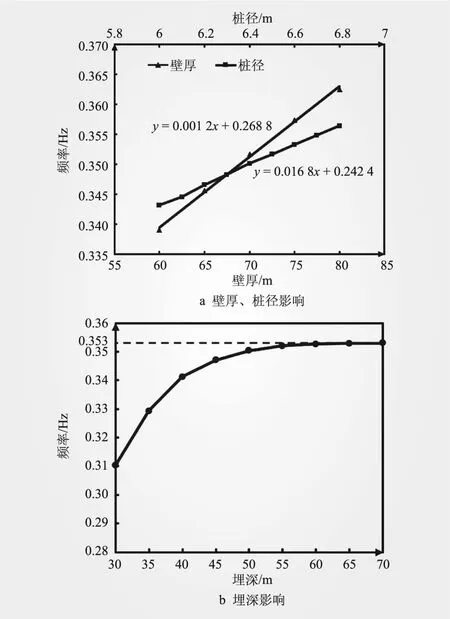
圖4 樁徑、壁厚與埋深對結(jié)構(gòu)頻率影響

樁徑與壁厚對結(jié)構(gòu)基頻的影響大致相同，兩者均與結(jié)構(gòu)基頻成線性相關，分別擬合散點圖得到曲線y=0.016 8x+0.242 4與y=0.001 2x+0.268 8，由圖4a可知，從剛度角度分析，樁徑的影響效果更大。

樁基礎埋深也是重要的影響因素，本文通過改變埋深，并保持泥面以上樁基礎尺寸不變以進行考慮。由圖4b可知，隨著埋深的增大，結(jié)構(gòu)的固有頻率先增大，后趨于穩(wěn)定，當埋深達到60 m(約為9倍樁徑)后，基頻穩(wěn)定于0.353 Hz。這是由于隨著埋深的增大，土體約束作用提高，其約束基本不再增加。

3.2 變徑段結(jié)構(gòu)影響

在變徑段結(jié)構(gòu)影響方面，主要考慮變徑段長度與變徑段相對位置對結(jié)構(gòu)基頻的影響，分別僅改變變徑段長度與變徑段上部長度，保持其他參數(shù)不變，結(jié)果如圖5所示。

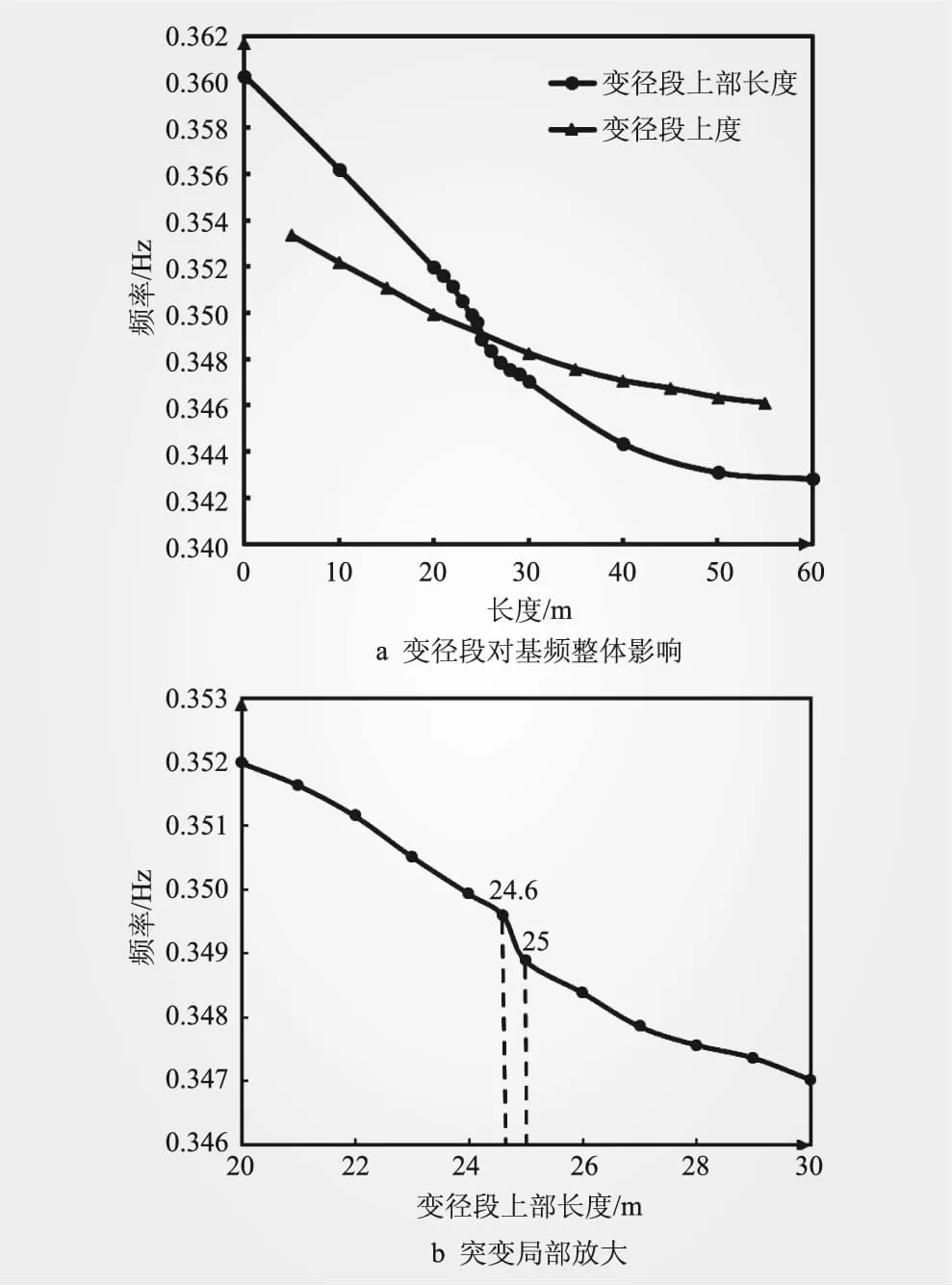
圖5 變徑段對結(jié)構(gòu)頻率影響

由圖5a可知，兩條曲線變化趨勢大致相同，結(jié)構(gòu)基頻均先減小后逐步穩(wěn)定，其實質(zhì)均為整體樁徑的相對減小。但顯然改變變徑段上部長度對整體樁徑的影響更大，并最終穩(wěn)定于0.343 Hz。

由于泥面以上樁基礎長度為24.6 m，故在20～30 m區(qū)間細化變徑段上部長度影響曲線，從放大圖(圖5b)得到結(jié)構(gòu)基頻在24.6～25 m降幅突增，當變徑段上部長度大于24.6 m，即整個變徑段開始處于泥面以下時，結(jié)構(gòu)基頻變化開始變緩，這是由于變徑段完全處于泥面以下后，土體對樁體的約束能力增強。

3.3 敏感性對比

由于上述參數(shù)計量單位以及變化范圍各不相同，為了消除參數(shù)間的量綱影響，能在同一變化范圍內(nèi)比較各參數(shù)對結(jié)構(gòu)基頻的影響程度，因此引入最值歸一化方法[17]，即對數(shù)據(jù)進行線性變換，將其映射至區(qū)間(0，1)進行比較，轉(zhuǎn)換公式為

(5)

式中，x、x*分別為各組數(shù)據(jù)中自變量與其最值歸一化處理的值；y、y*分別為各組數(shù)據(jù)中因變量與其最值歸一化處理的值；xmin、xmax分別為各組數(shù)據(jù)中自變量最小值、最大值；ymin、ymax分別為各組數(shù)據(jù)中因變量最小值、最大值。

整理上述結(jié)果，繪制歸一化處理后各參數(shù)匯總?cè)鐖D6所示。由圖6可知，上述6個敏感性因素可以分為2大類，線性變化因素與非線性變化因素，線性變化因素包括樁徑與壁厚，非線性變化因素包括水深、埋深、變徑段長度與相對位置。在非線性變化因素中，埋深對基頻為正影響，在前期其影響程度最大，隨后逐漸趨于穩(wěn)定，而其他3個因素對基頻為負影響，變徑段長度與上部長度的影響程度類似，有逐漸趨于穩(wěn)定趨勢，水深因素則隨著不斷增大，影響程度也不斷加大。因此，在實際工程中，可據(jù)此對結(jié)構(gòu)進行適當調(diào)整，從而可調(diào)整結(jié)構(gòu)基頻達到避振效果。

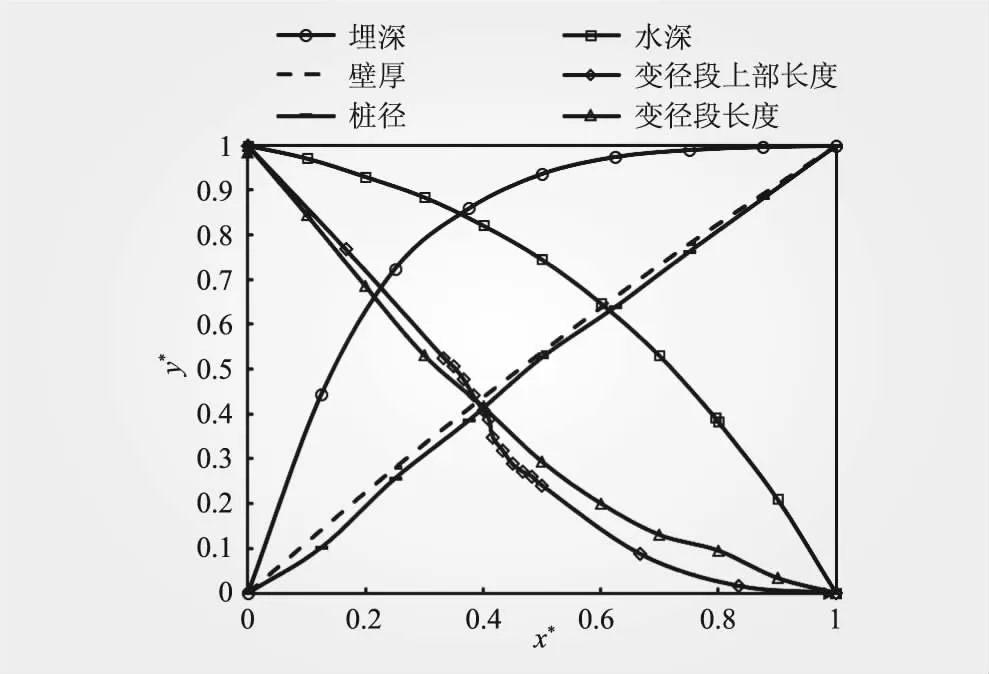
圖6 歸一化處理后各影響因素參數(shù)匯總

4 結(jié) 論

本文利用ABAQUS有限元軟件，通過建立塔筒-變徑樁基礎-土體的實體模型，對整體結(jié)構(gòu)的動力特性進行簡單分析，針對變徑樁基礎展開模態(tài)敏感性分析，得到如下結(jié)論：

(1)利用ABAQUS計算得到風機塔筒結(jié)構(gòu)的基頻為0.351 Hz，結(jié)構(gòu)振型主要呈現(xiàn)擺動與彎曲，且風機前兩階頻率與葉片3P頻率具有一定的重合度，可能產(chǎn)生共振。

(2)本文利用附加質(zhì)量法來模擬海水，通過對比發(fā)現(xiàn)，考慮水深使得結(jié)構(gòu)的各階頻率都有所下降，且隨著水深的增加，結(jié)構(gòu)基頻下降幅度增大，引起共振的可能性增大。因此對于處于深水區(qū)的結(jié)構(gòu)，考慮海水因素十分必要。

(3)在對變徑樁基礎進行敏感性分析時，結(jié)構(gòu)基頻隨著樁徑、壁厚的增加線性增加，且樁徑影響更顯著，埋深對基頻為正影響，在前期其影響程度最大，隨后逐漸趨于穩(wěn)定。

(4)變徑段相對位置與長度的影響類似，均先減小后有穩(wěn)定趨勢，且變徑段相對位置對基頻的影響會在泥面處發(fā)生突變，降幅增大。因此在實際工程中，可據(jù)此對結(jié)構(gòu)進行適當調(diào)整，從而在一定程度上達到避振效果。