考慮電力牽引鏈路非線性損耗的列車節(jié)能駕駛方法

肖 壯，馮曉云，王青元，孫鵬飛，黃德青

(西南交通大學 電氣工程學院，四川 成都 611756)

軌道交通車輛作為能效最高的公共交通工具，得到了快速發(fā)展和廣泛應(yīng)用。隨著運營規(guī)模的不斷擴大，列車運行總能耗顯著增加。牽引驅(qū)動能耗占總能耗的50%以上[1]，包括克服阻力做功、電力牽引系統(tǒng)和牽引供電系統(tǒng)損耗三大部分。因此，研究考慮電力牽引鏈路非線性損耗的列車節(jié)能駕駛方法，將有助于減小系統(tǒng)損耗，進一步降低列車運行能耗，提升系統(tǒng)效能[2]。

目前，研究列車節(jié)能駕駛策略一般以輪周機械能最小為優(yōu)化目標[3-4]。文獻[5-6]基于極大值原理分析得到列車節(jié)能工況，包括全力牽引、恒速牽引、惰行和全力制動。在此基礎(chǔ)上，文獻[7]考慮再生制動能量利用，分析得到最優(yōu)工況還包含恒速電制動。文獻[8-9]分別基于遺傳算法和粒子群算法等啟發(fā)式算法計算列車節(jié)能操縱策略。文獻[10-11]基于動態(tài)規(guī)劃算法設(shè)計了列車正點節(jié)能操縱算法，降低了列車運行能耗。該方法可以有效處理模型非線性，得到最優(yōu)解。

以上方法忽略了列車牽引鏈路非線性損耗，輪周機械能最小并不意味著列車運行電能最小[12]。電力牽引系統(tǒng)結(jié)構(gòu)復雜，運行過程存在電-磁-熱-機械能間的轉(zhuǎn)換，系統(tǒng)損耗機理建模復雜度高[12]。實測數(shù)據(jù)表明，電力牽引系統(tǒng)損耗與列車牽引力和運行速度有關(guān)[13-14]。此外，牽引供電系統(tǒng)存在非線性傳輸損耗，其損耗大小由負載功率和列車位置決定，均與列車駕駛策略直接相關(guān)。

本文以地鐵列車節(jié)能駕駛為研究對象，結(jié)合實測數(shù)據(jù)和系統(tǒng)模型建立牽引鏈路非線性損耗模型，包括電力牽引和牽引供電系統(tǒng)損耗。綜合考慮列車動力學模型、運行約束條件(線路限速，坡道，運行時間)和系統(tǒng)損耗，構(gòu)建節(jié)能運行最優(yōu)控制模型。結(jié)合極大值原理和動態(tài)規(guī)劃方法，設(shè)計一種滿足運行約束條件的節(jié)能優(yōu)化算法。通過仿真案例對比不同能耗模型對節(jié)能駕駛方案的影響。

1 列車縱向動力學模型

列車運行速度由牽引力、制動力、基本運行阻力和坡道附加阻力共同決定。結(jié)合受力分析和牛頓第二定律，其變化規(guī)律可以描述為

( 1 )

列車運行時間變化可以表示為

( 2 )

式中：s為列車運行位置；v為列車運行速度；t為列車運行時間；M為列車質(zhì)量；γ為回轉(zhuǎn)質(zhì)量系數(shù)；Fb為空氣制動力；Ft為牽引電機產(chǎn)生的牽引力/電制動力，F(xiàn)t大于0為牽引力，F(xiàn)t小于0為電制動力；F0(v)為列車速度為v時的基本運行阻力；Fs(s)為列車在s處的附加阻力。

根據(jù)文獻[15]，基本運行阻力包含列車運行過程中的風阻和輪軌摩擦阻力，可表示為車速的二次函數(shù)；附加阻力包含坡道附加阻力和曲線附加阻力，分別可以表示為

F0(v)=a+bv+cv2

( 3 )

Fs(s)=Mgsinα+MgR/r

( 4 )

式中：a、b、c均為常數(shù)，具體數(shù)值由列車類型確定；R為常數(shù)，通常取600；α為線路坡度值；r為曲線半徑。

列車輪周機械功率Pt為

Pt=Ft·v

( 5 )

2 牽引鏈路非線性損耗模型

2.1 列車運行能耗組成

列車運行能量傳遞過程如圖1(a)所示，圖1(a)中，E1r為運行阻力損耗，Ebl為制動損耗，Ebr為再生制動能量，Ele為電力牽引系統(tǒng)損耗，Elc為牽引供電系統(tǒng)損耗。通過受電弓與接觸網(wǎng)接觸，電能從牽引變電站流入列車電力牽引系統(tǒng)，電流在變電站和接觸網(wǎng)傳輸過程中產(chǎn)生損耗Elc。電力牽引系統(tǒng)通過牽引變流器和牽引電機，將電能變換為機械能，此過程中產(chǎn)生系統(tǒng)損耗Ele。輪對機械能主要用于克服基本運行阻力和線路附加阻力，產(chǎn)生損耗Elr。同時，列車制動過程包含電制動和空氣制動兩種方式，空氣制動會造成制動損耗Ebl，而部分電制動能量可反饋回牽引網(wǎng)，供其他列車牽引使用，該部分能量為Ebr。

牽引鏈路功率損耗主要包含接觸網(wǎng)供電、電力牽引系統(tǒng)和齒輪傳動系統(tǒng)，如圖1(b)所示。當列車運行于牽引或惰行工況時，接觸網(wǎng)供電系統(tǒng)存在變電站損耗Pt-ts和接觸網(wǎng)傳輸損耗Pt-imp；電力牽引系統(tǒng)存在逆變器損耗Pt-inv和牽引電機損耗Pt-mot；齒輪傳動系統(tǒng)存在損耗Pt-gear。當列車運行于再生制動工況時，齒輪傳動系統(tǒng)、牽引電機、逆變器和牽引網(wǎng)損耗分別為Pb-gear、Pb-mot、Pb-inv和Pb-imp。

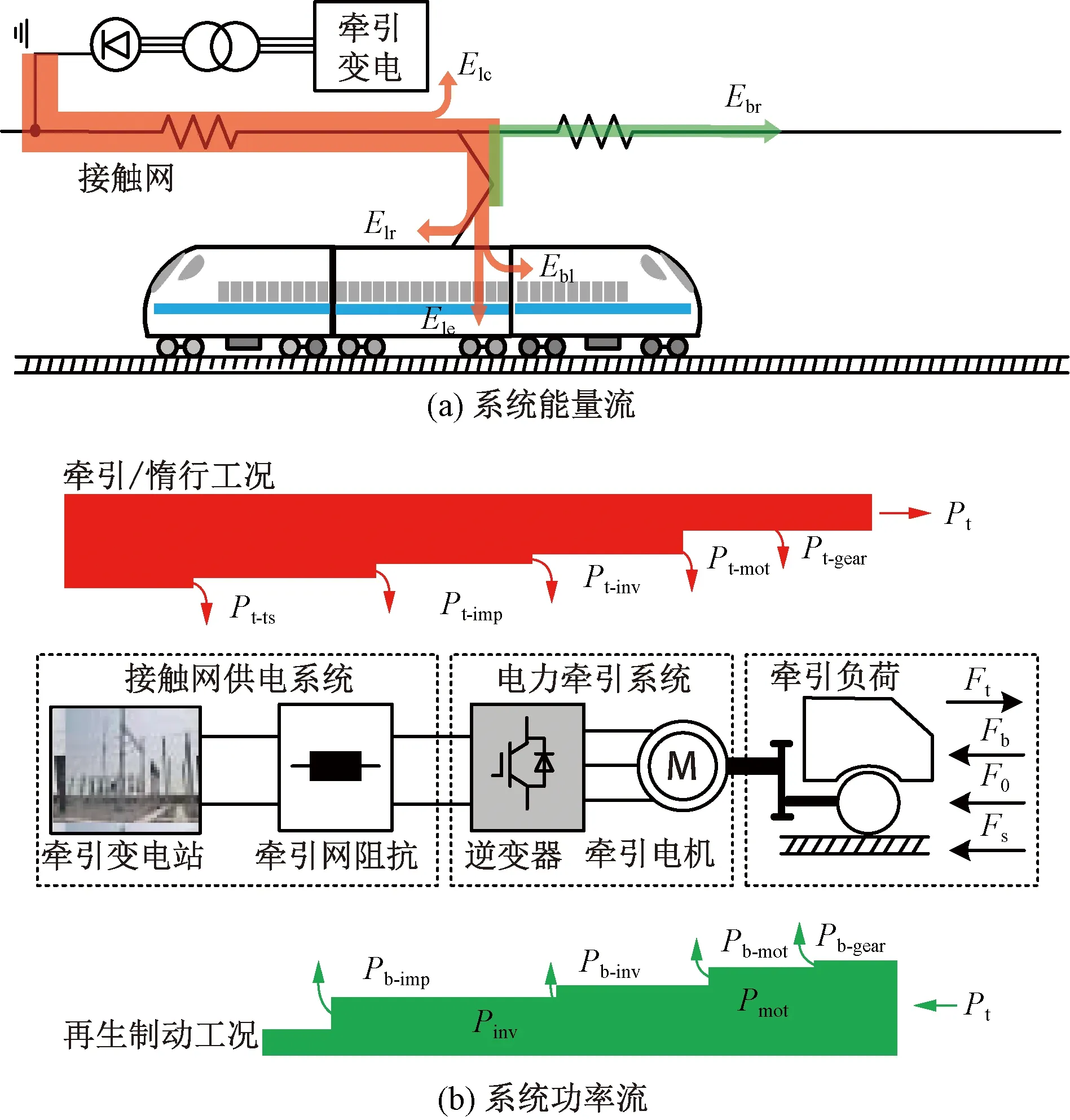
圖1 列車運行能量流和功率流

2.2 電力牽引系統(tǒng)損耗模型

電力牽引系統(tǒng)損耗大小與列車負載功率直接相關(guān)，受運行速度和牽引力的影響[13-14]。同時，牽引工況和制動工況時損耗的產(chǎn)生方式和數(shù)值大小存在差異。因此，本文基于實車運行數(shù)據(jù)，采用最小二乘方法分別建立牽引工況和制動工況列車全速域運行損耗模型，以更準確的表征系統(tǒng)損耗。

以列車運行速度和牽引力大小作為自變量，以系統(tǒng)損耗作為因變量，根據(jù)均方根誤差RMSE評估自變量不同階次的擬合效果。牽引工況和制動工況對應(yīng)的損耗關(guān)系如圖2所示。

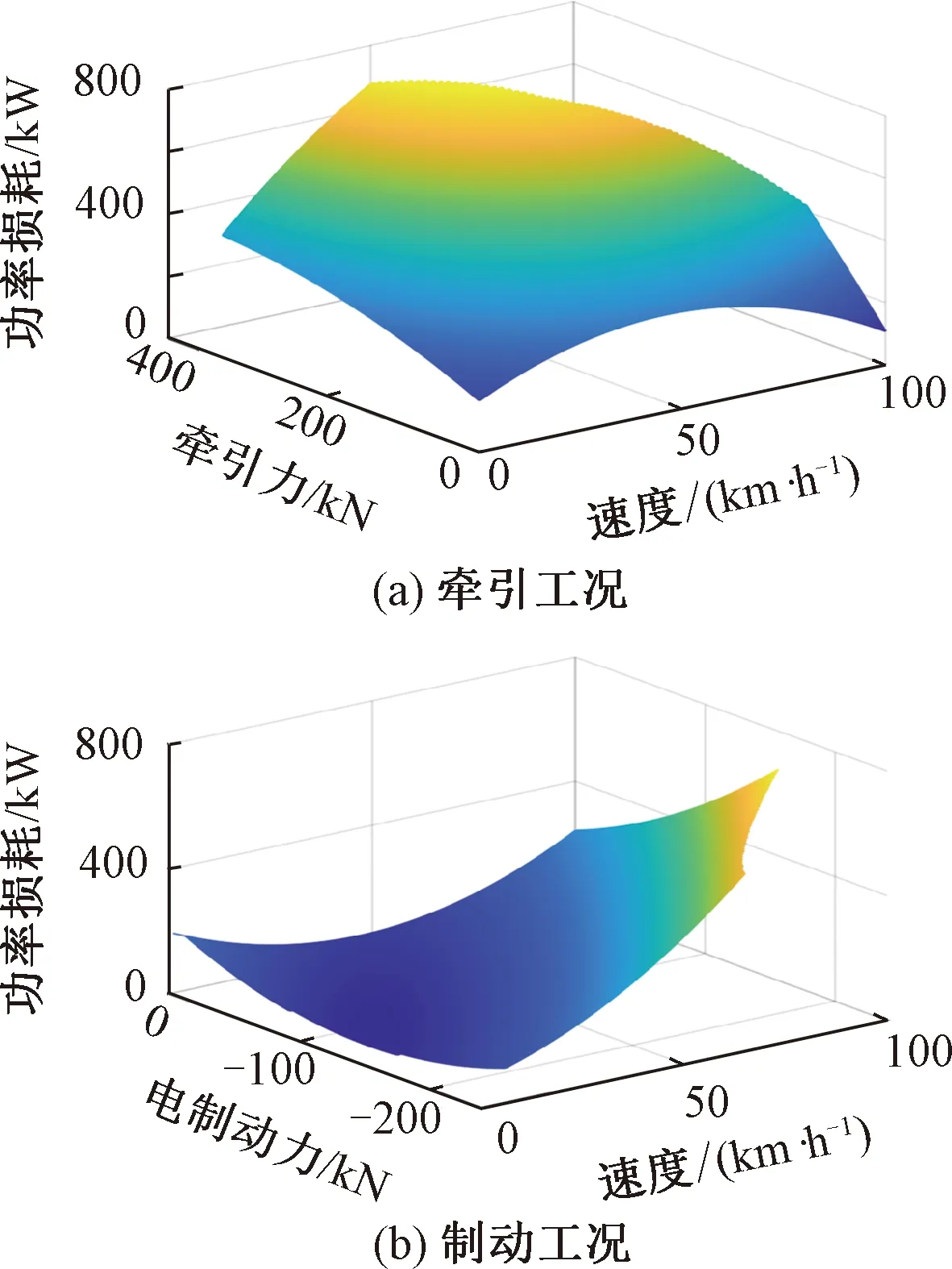
圖2 電力牽引系統(tǒng)功率損耗

損耗值Pl與牽引力/電制動力、速度間的關(guān)系可以表示為

( 6 )

2.3 接觸網(wǎng)損耗模型

直流雙邊供電方式的牽引網(wǎng)等效電路模型如圖3所示。采用理想電壓源V0和內(nèi)阻R0等效表征牽引變電站輸出外特性。It1、It2分別為兩側(cè)變電站的輸出電流。接觸網(wǎng)內(nèi)阻采用分布參數(shù)電阻模型等效，阻值大小與相對應(yīng)的接觸網(wǎng)長度成正比。當相鄰兩個車站間的距離為l、牽引變電站與對應(yīng)車站的距離分別為L1和L2時，列車與牽引變電站的距離分別為s+L1和l+L2-s。因此，電阻值R1、R2、R3、R4可以表示為

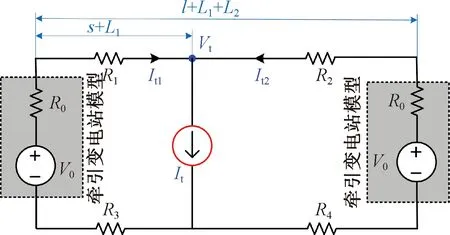
圖3 牽引網(wǎng)等效電路模型

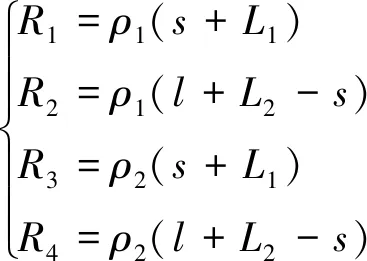
( 7 )

式中：ρ1為接觸網(wǎng)電阻率；ρ2為走行軌電阻率。

從功率發(fā)揮角度，列車電功率Pinv包含輪周機械功率Pt和電力牽引系統(tǒng)損耗Pl。

Pinv=Pt+Pl

( 8 )

從供電角度，列車所在位置的接觸網(wǎng)網(wǎng)壓為Vt，流經(jīng)列車的等效電流為It。以列車輪對與鋼軌接觸點為零電勢參考點，結(jié)合等效電路中電壓、電流關(guān)系，列車電功率Pinv和牽引變電站輸出總功率Ps分別為

Pinv=(It1+It2)·Vt=

( 9 )

Ps=(It1+It2)·V0=

(10)

結(jié)合式( 8 )、式( 9 )，可根據(jù)列車牽引力和運行速度計算接觸網(wǎng)網(wǎng)壓Vt。在此基礎(chǔ)上，根據(jù)式(10)可以計算牽引變電站輸出功率。

牽引網(wǎng)仿真參數(shù)見表1。為驗證供電模型的正確性，以列車ATO操縱結(jié)果(牽引力和速度曲線)為輸入?yún)?shù)，對比仿真計算和實測接觸網(wǎng)電壓Vt、列車等效電流It的變化情況，結(jié)果如圖4所示。由圖4可知，模型計算與實測數(shù)據(jù)較為一致，仿真計算模型準確性較好。

表1 牽引供電系統(tǒng)參數(shù)

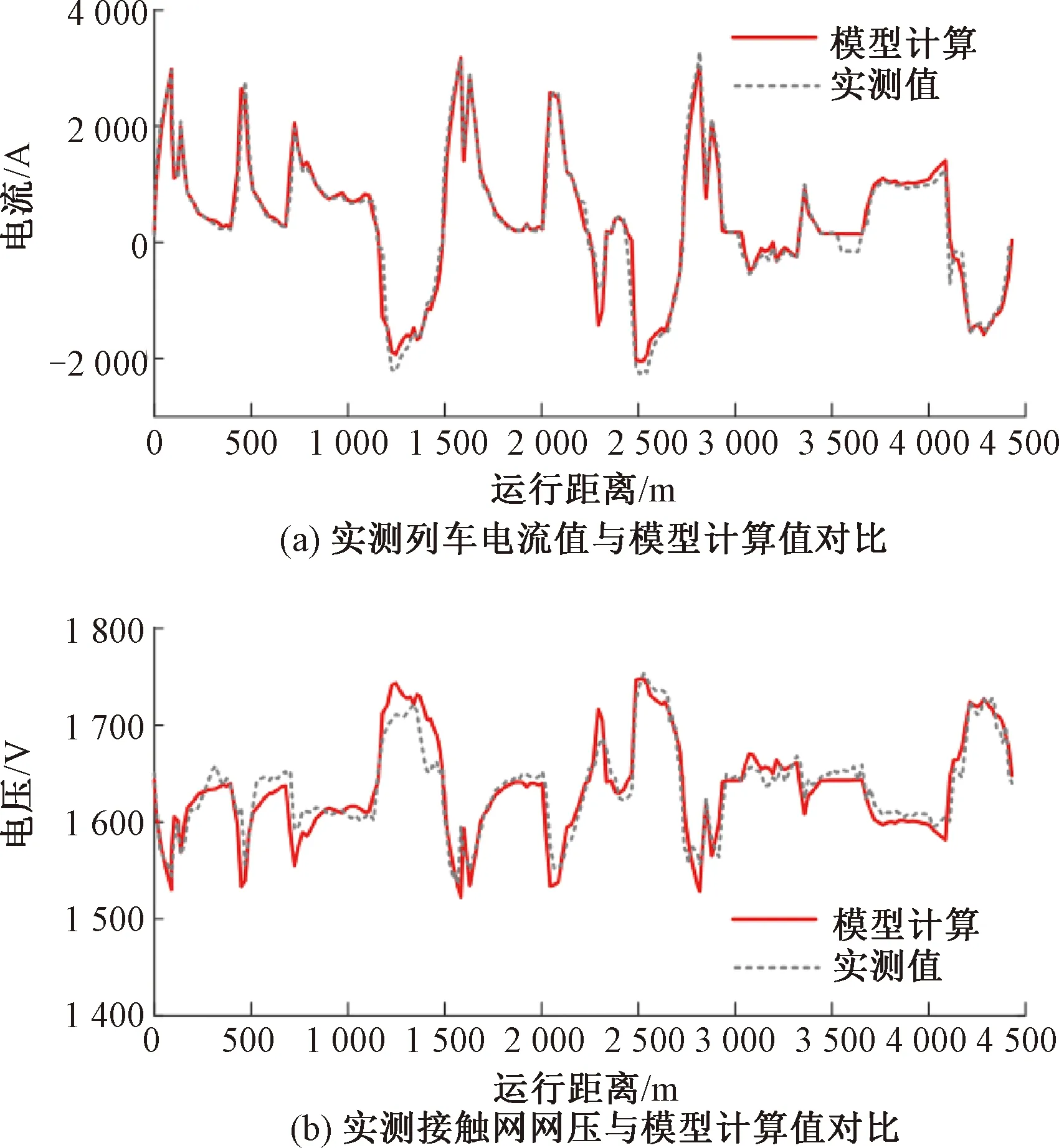
圖4 牽引網(wǎng)等效電路計算模型驗證

3 最優(yōu)控制分析與優(yōu)化算法

3.1 節(jié)能最優(yōu)控制問題

考慮列車牽引鏈路非線性損耗，以牽引變電站輸出能耗最小為目標，建立節(jié)能最優(yōu)控制模型，目標函數(shù)為

(11)

(12)

式中：Peq為列車運行等效功率；η為等效再生制動利用率[7]。

列車運行過程受到動力學方程式( 1 )、式( 2 )約束，同時還受自身牽引/制動性能、線路限速和接觸網(wǎng)供電電壓等約束。

Fmin(v)≤Ft(s)≤Fmax(v)

(13)

v(s)≤vlim(s)

(14)

Vmin≤Vt≤Vmax

(15)

式中：vlim(s)為線路限速；Fmin(v)和Fmax(v)分別為最大電制動力和最大牽引力；Vmin和Vmax分別為接觸網(wǎng)電壓的最小和最大值。

同時，列車運行過程還受到起點、終點速度以及線路時刻表的限制。

v(s0) =v(sf) = 0

(16)

t(sf)-t(s0)=T

(17)

式中：T為準點運行時間。

節(jié)能最優(yōu)控制問題包含運行速度v和時間t兩個狀態(tài)變量以及電機控制力Ft(s)和空氣制動力Fb(s)兩個控制變量。該問題是一個多變量、非線性最優(yōu)控制問題。

3.2 極大值原理分析

采用極大值原理分析節(jié)能最優(yōu)控制問題，首先，構(gòu)建Hamiltonian函數(shù)

(18)

式中：λt和λv分別為運行時間t和速度v對應(yīng)的伴隨變量。

由式(18)可知，哈密頓函數(shù)不顯含時間t，則有

(19)

即λt為一個恒定常數(shù)，其具體數(shù)值由運行時間約束式(17)確定。

3.3 動態(tài)規(guī)劃算法

本文采用動態(tài)規(guī)劃算法求解節(jié)能速度曲線。對于多維狀態(tài)的優(yōu)化問題，動態(tài)規(guī)劃算法可能會產(chǎn)生“維數(shù)災(zāi)難”[11]。依據(jù)極大值原理的分析，對于一個確定運行區(qū)間，λt為常數(shù)。因此，可將運行時間以等效能耗的形式考慮進目標函數(shù)。這樣節(jié)能最優(yōu)控制問題僅包含運行速度v一個狀態(tài)變量，改變λt的數(shù)值大小可改變優(yōu)化速度曲線，進而影響區(qū)間運行時間。目標函數(shù)J為

(20)

以等距離步長Δs將式(20)離散化，連續(xù)模型轉(zhuǎn)化為離散形式為

(21)

式中：N為離散化階段數(shù)。

為縮小可行解空間，首先根據(jù)線路條件(限速和坡道)、列車動力性能(牽引/制動性能和基本阻力特性)計算列車運行最大能力速度曲線，計算步驟為:

Step1以線路限速將運行過程劃分為多個恒速區(qū)間，起點和終點視為兩個速度為0的點恒速區(qū)。

Step2連接各恒速區(qū)。當相鄰兩恒速區(qū)的速度值出現(xiàn)正向變化，即后一恒速區(qū)速度值大于前一恒速區(qū)，則采用最大牽引工況從前一恒速區(qū)末端加速運行，直至速度等于后一恒速區(qū)的速度值；若牽引運行至該恒速區(qū)的末端點，速度仍小于目標恒速值，則調(diào)整該區(qū)間恒速速度至末端點速度。當相鄰兩恒速區(qū)的速度值出現(xiàn)負向變化，即后一恒速區(qū)速度值小于前一恒速區(qū)，則采用最大制動工況從前一恒速區(qū)末端反向計算，直至速度曲線產(chǎn)生交點。

最大能力速度曲線限制了區(qū)間運行的速度邊界，即優(yōu)化速度曲線必然小于最大能力速度曲線。在此基礎(chǔ)上將列車區(qū)間運行過程按距離離散化為多個階段，在每個階段求解最優(yōu)狀態(tài)轉(zhuǎn)移過程，得到節(jié)能優(yōu)化速度曲線，如圖5所示。

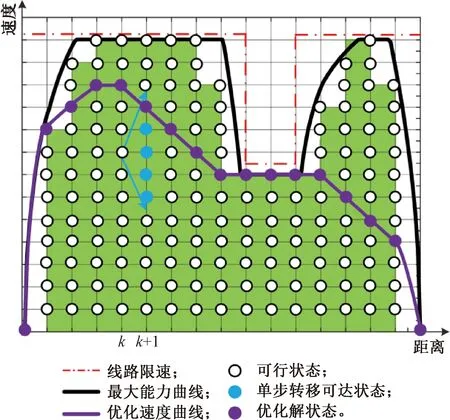
圖5 動態(tài)規(guī)劃求解過程示意

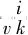
(22)

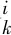
后向DP算法開始于k=N-1階段。考慮到終點位置的速度為0，其對應(yīng)的能耗函數(shù)為

(23)

動態(tài)規(guī)劃算法計算步驟為:

Step1分別以Δs和Δv為步長離散化線路距離和速度，N=(sf-s0)/Δs。

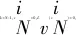
Step3重復Step2直至k=1，確定節(jié)能優(yōu)化速度曲線、牽引/制動控制量和區(qū)間運行時間tsum。

Step4對比區(qū)間運行tsum和給定運行時間T，若條件|T-tsum|<ε成立，則優(yōu)化計算結(jié)束，否則調(diào)整等效因子λt，重新執(zhí)行Step2～Step4。

4 仿真驗證

4.1 仿真條件

采用實際運營地鐵線路，所選仿真區(qū)段包含4座車站，全長4.2 km，時刻表給定的各站A—B、B—C、C—D運行時間分別為94、86、108 s。動態(tài)規(guī)劃算法中各參數(shù)取值分別為Δs=5 m、Δv=0.5 km/h、ε=0.5 s。

4.2 節(jié)能優(yōu)化策略

分別以輪周機械能最小化，考慮電力牽引系統(tǒng)非線性損耗后列車電能最小化和考慮牽引鏈路損耗后變電站電能最小化為目標，采用動態(tài)規(guī)劃算法求解。不同目標函數(shù)的優(yōu)化速度曲線和實測ATO駕駛結(jié)果如圖6所示。

圖6 不同優(yōu)化目標與ATO駕駛曲線對比

考慮牽引鏈路損耗后，列車節(jié)能運行策略發(fā)生變化。結(jié)合圖6可知，機械能最小化策略采用全牽加速-恒速-惰行-最大制動的工況控制序列，惰行控制可有效利用區(qū)間運行富裕時間，降低列車牽引機械能。考慮系統(tǒng)損耗后，惰行工況會造成電力牽引系統(tǒng)和牽引供電系統(tǒng)損耗。列車電能最小化和變電站電能最小化方式均采用小功率再生制動工況取代了惰行工況，再生制動功率補償系統(tǒng)損耗，避免牽引系統(tǒng)電能損耗。

不同運行策略能耗見表2。基本阻力損耗與列車運行速度的平方成正比，運行速度波動越大，對應(yīng)的基本阻力損耗越大。ATO駕駛對應(yīng)的基本阻力損耗最大，機械能最小化方式阻力損耗最小。機械能最小化方式可得到最小的輪周牽引能耗和電制動能量；ATO駕駛方式輪周牽引能耗和電制動能量均最大，其駕駛策略存在牽引與制動工況的切換，造成了不必要的系統(tǒng)損耗，增加列車運行能耗。

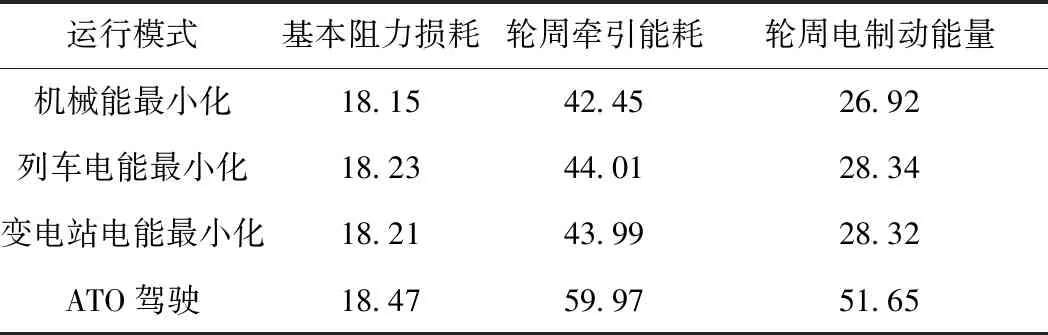
表2 不同優(yōu)化目標與ATO駕駛能耗比較 kW·h

從輪周機械能的角度，機械能最小化策略運行能耗最小。但是輪周機械能并不能真實表征列車運行電能耗。因此，需要從系統(tǒng)電能消耗的角度進一步分析列車運行能耗。

4.3 電力牽引系統(tǒng)非線性損耗影響分析

根據(jù)式( 6 )計算不同運行策略對應(yīng)的電力牽引系統(tǒng)功率損耗，如圖7(a)所示。列車運行所需電功率曲線如圖7(b)所示。列車電能最小化駕駛方式在途中運行時，通過小功率電制動使得再生制動功率與電力牽引系統(tǒng)損耗相等，實現(xiàn)降低系統(tǒng)運行能耗的目的。機械能最小化策略采用惰行工況，列車電力牽引系統(tǒng)損耗較大，增大了列車網(wǎng)側(cè)牽引能耗。

表3統(tǒng)計了不同駕駛方式網(wǎng)側(cè)能耗情況，列車電能最小化方式可有效降低電力牽引系統(tǒng)損耗，實現(xiàn)網(wǎng)側(cè)牽引能耗最小化。

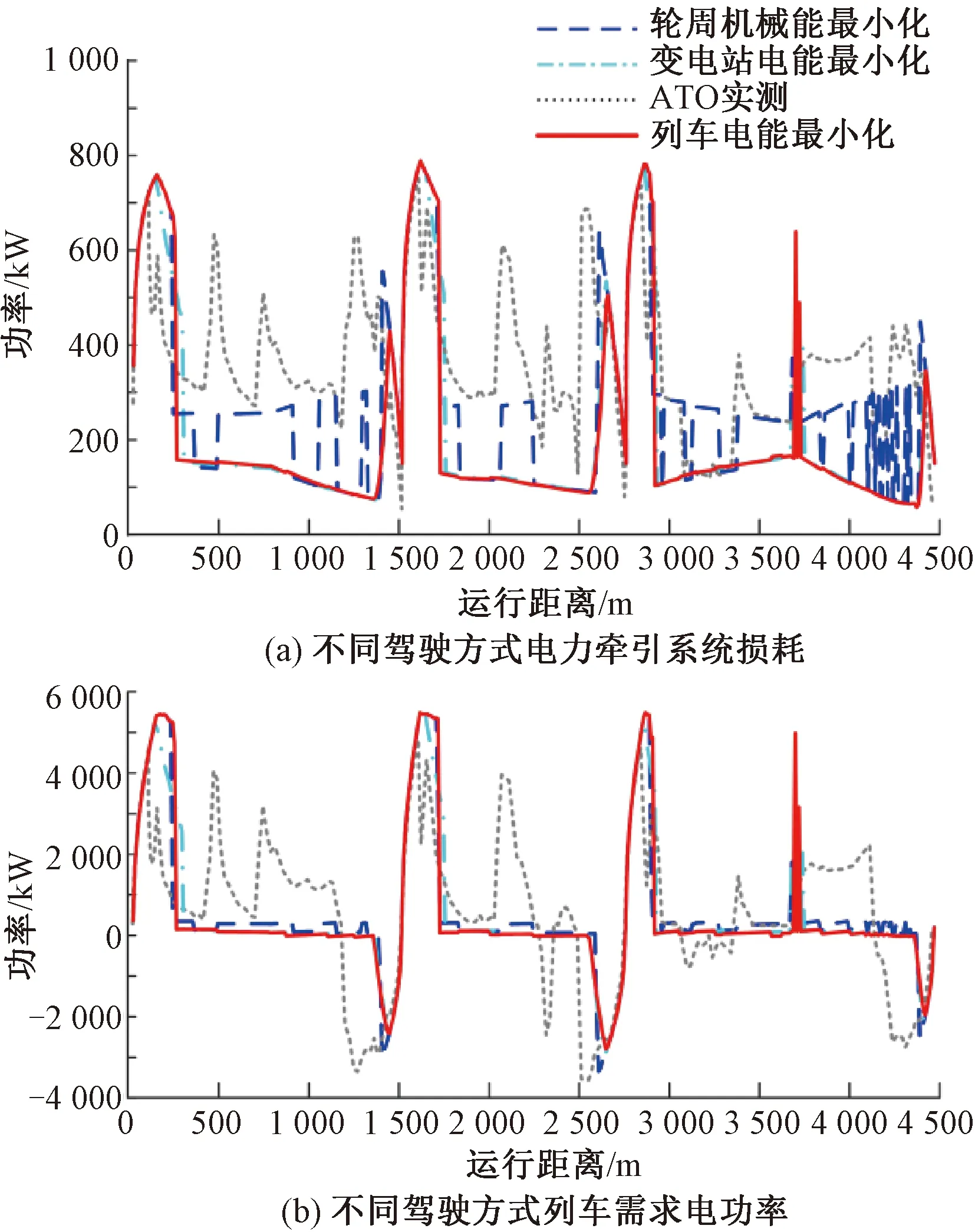
圖7 電力牽引系統(tǒng)損耗對不同駕駛方式能耗的影響

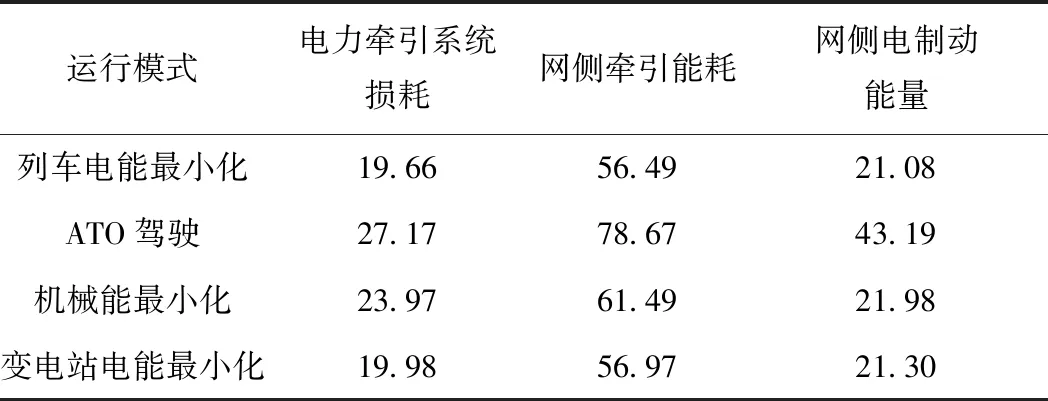
表3 不同駕駛方式網(wǎng)側(cè)能耗比較 kW·h

4.4 接觸網(wǎng)非線性損耗影響分析

不同駕駛方式對應(yīng)的接觸網(wǎng)功率損耗和接觸網(wǎng)網(wǎng)壓變化曲線如圖8所示。接觸網(wǎng)功率損耗僅考慮列車需求電功率為正的情況。列車需求電功率為負數(shù)表明列車處于再生制動工況，此部分能量以等效能耗方式計入單列車運行能耗。由圖8(b)可知，變電站電能最小化方式可有效減小網(wǎng)壓波動范圍。

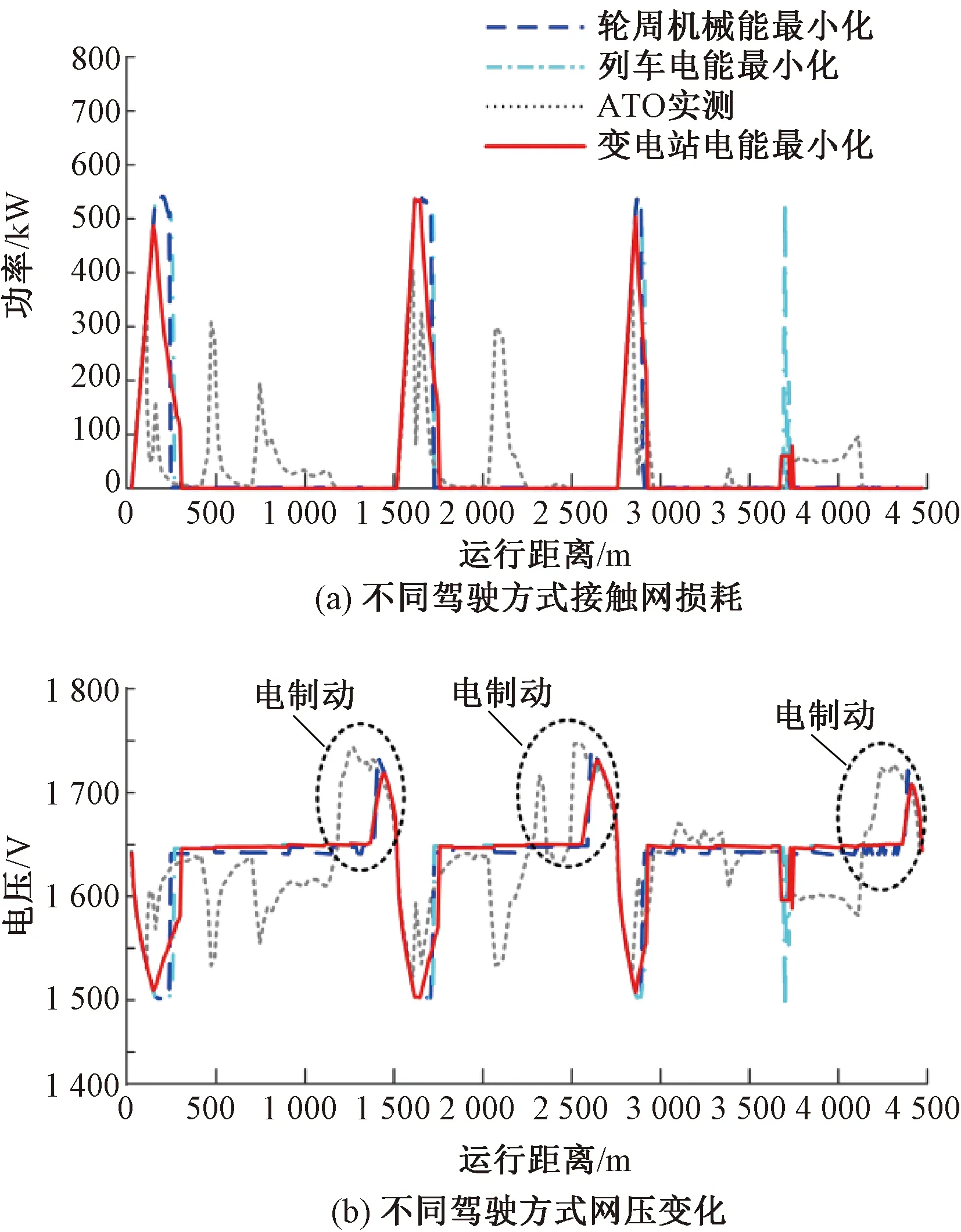
圖8 接觸網(wǎng)損耗和網(wǎng)壓變化對比

列車運行能耗對比見表4。接觸網(wǎng)損耗在總運行能耗中占比相對較小，變電站能耗最小化方式可有效降低接觸網(wǎng)損耗，實現(xiàn)變電站牽引能耗最小化。

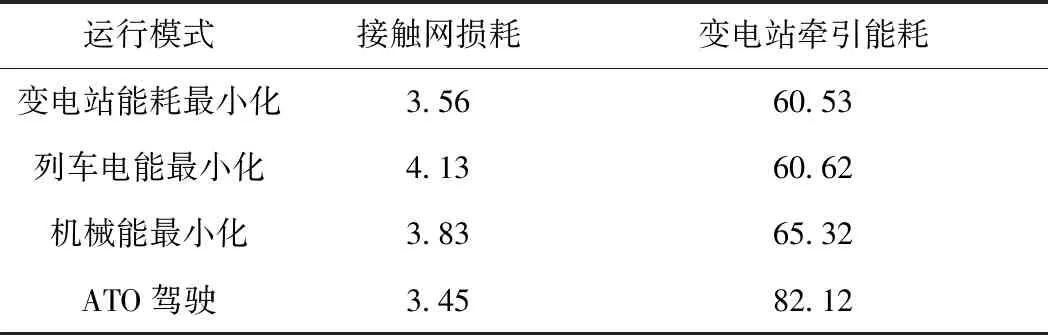
表4 不同駕駛方式接觸網(wǎng)能耗比較 kW·h

4.5 節(jié)能效果分析

列車運行損耗主要包含基本阻力損耗、電力牽引系統(tǒng)損耗、接觸網(wǎng)損耗和制動損耗。其中，電力牽引系統(tǒng)損耗和制動損耗占比較大，且與列車運行策略直接相關(guān)。基本阻力損耗主要受列車運行速度波動的影響，電力牽引系統(tǒng)損耗由列車牽引、制動力的大小決定。

單列車的運行能耗采用等效計算方式。等效牽引即變電站牽引能耗與等效利用的網(wǎng)側(cè)電制動能耗之差。城市軌道交通發(fā)車密度較大，約60%的電制動能量可被有效吸收[4,16]。表5給出了不同運行方式對應(yīng)的變電站等效牽引能耗。可以看出，變電站能耗最小化駕駛方式可以綜合考慮各子系統(tǒng)損耗，實現(xiàn)變電站輸出能耗最小化。

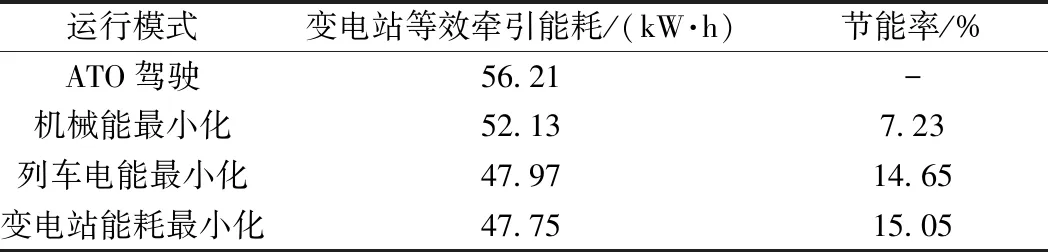
表5 不同駕駛方式變電站等效能耗比較

5 結(jié)論

本文提出一種考慮電力牽引鏈路非線性損耗的列車節(jié)能運行優(yōu)化方法，通過優(yōu)化結(jié)果與實測ATO系統(tǒng)駕駛結(jié)果對比，驗證了模型和方法的有效性，得到結(jié)論如下：

(1)基于運行數(shù)據(jù)擬合的列車電力牽引系統(tǒng)損耗模型能夠有效反映列車運行非線性損耗特性，準確表征列車運行過程能耗。

(2)通過極大值原理推導，證明了以能耗和時間加權(quán)求和為目標的動態(tài)規(guī)劃算法可獲得理論最優(yōu)解。該方法可同時兼顧節(jié)能和準點兩個全局指標。

(3)考慮牽引鏈路非線性損耗最小化的列車節(jié)能優(yōu)化方法可最大化降低列車運行能耗，提升系統(tǒng)效能。同時，牽引鏈路損耗模型使得在部分運行區(qū)段小功率電制動工況會取代惰行工況。

此外，本文主要分析單列車的節(jié)能駕駛問題，后續(xù)研究將重點考慮多列車運行場景下的節(jié)能駕駛和再生制動能量利用。