成網條件下基于運行圖鋪畫的高速鐵路通過能力計算研究
王宇強,魏玉光,林 楓
(1.中國鐵道科學研究院集團有限公司 運輸及經濟研究所, 北京 100081;2.北京交通大學 交通運輸學院,北京 100044)
近年來,我國高速鐵路(以下簡稱“高鐵”)迅猛發展,客運需求逐年攀升,形成了以“四縱四橫”為基礎的高鐵路網,且我國高鐵運營情況復雜,不同速度等級的本線及跨線列車混合運行,如何準確計算高鐵通過能力且在有限的時空資源內開行更多的列車成為亟需解決的問題。
目前關于高鐵通過能力計算的研究主要為扣除系數法[1]、平均最小列車間隔時間法[2]、計算機模擬法[3-4]和基于UIC 406的運行圖壓縮及加密法[5],但現有研究或沿用既有線通過能力計算方法,或采用國外的通過能力計算法,或在計算過程中沒有考慮占比較大的跨線列車,從而可能導致計算結果不夠精確。高鐵運行圖鋪畫問題,可視為多商品流問題,列車作為商品占用高鐵有限的時空資源,目標函數一般為最小化列車運行(等待)時間,最小化重新鋪畫后列車運行圖與現有運行圖的差異,最大化運營收益和最大化列車開行數。在解決運行圖鋪畫問題的小規模案例時,可采用商業求解器(如CPLEX)得到精確解,但當處理大規模案例時,必須使用啟發式算法或分解算法來求解模型,目前使用較多的分解算法包括:拉格朗日松弛法、ADMM、列生成法、D-W分解法等。文獻[6-7]基于累計流變量模型鋪畫列車運行圖,使用拉格朗日松弛算法求解;文獻[8]構建擴展時空網絡以解決周期運行圖問題,采用ADMM分解算法求解;文獻[9]構建整數規劃模型,在鋪畫列車運行圖的同時考慮客流需求,最后采用列生成算法求解;文獻[10]提出一種整數規劃模型來鋪畫列車運行圖,旨在最大化運營收益,設計了啟發式算法求解;文獻[11]以最大化列車開行數為目標鋪畫列車運行圖,構建整數規劃模型,采用D-W分解法求解。
以上研究對車站因素的影響仍采用傳統的簡化處理方法,尤其是繁忙干線上銜接多方向的高鐵樞紐,本線列車與跨線列車混合運行沖突干擾產生的影響未能得到深入研究,導致高鐵列車運行圖編制質量難以突破樞紐瓶頸的制約。文獻[12]注意到這一問題的重要性,但未能提出具體有效的量化解決方法。文獻[13]將車站設定為虛擬區間,提出基于點線一體化的高鐵通過能力計算方法,在此基礎上,本文研究將高鐵樞紐這一虛擬區間內的通過能力利用細化為被各種列車弧占用的描述方法,以站場實際布局和列車徑路疏解方式為基本依據,將不同方向列車在跨線樞紐站的沖突用車站最小列車間隔時間來表示,構建目標函數為最大化列車開行數量的整數規劃模型,采用ADMM將復雜的列車組合優化問題分解為尋找單個列車的最短路問題,從而獲得各方向列車在跨線樞紐接發和通過的最佳配合方式,最后得到更符合實際情況的運行圖鋪畫結果。
1 問題描述
符號及其定義見表1。

表1 符號說明
本文進一步從優化高鐵樞紐跨線列車運行組織的角度研究高鐵運行圖鋪畫問題,力求在有限的高鐵時空資源中開行更多列車,進而計算高鐵通過能力。高鐵物理網(N,L)見圖1(a),包括車站集合N和運行區段集合L。為方便表示列車在物理網中的各種作業過程,采用文獻[13]提出的方法構建虛擬區間,將一個車站拆分為若干物理點,將物理網擴展為服務網(N′,A),擴展后的高鐵服務網見圖1(b),包括物理點集合N′和物理弧集合A,列車在服務網中的作業過程(列車停站、列車運行和列車跨線等)為弧(i,j)∈A,表示列車從物理點i∈N′到物理點j∈N′。將起點站拆分為列車虛擬起點、列車到達點和列車出發點;將終點站拆分為列車到達點、列車出發點和列車虛擬終點;將其他車站拆分為列車虛擬起點、列車到達點、列車出發點和列車虛擬終點。車站的拆分過程及各類弧的構建見圖1(b),列車生成弧、列車到達弧、列車停站弧、列車跨線弧以及列車運行弧分別表示列車生成、列車消失、列車停站作業、列車跨線作業以及列車運行。跨線列車在跨線站2只能通過跨線弧到達車站4。
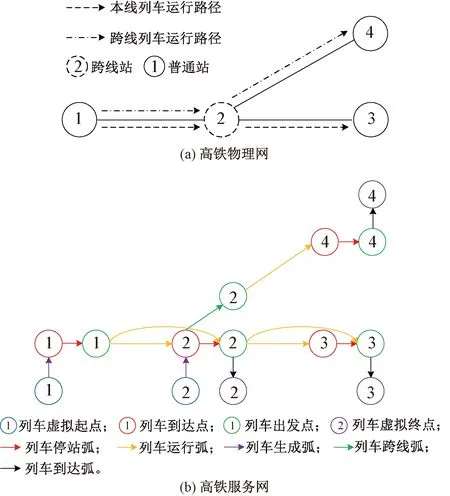
圖1 高鐵物理網與服務網的構建
時空網可以很好地反映列車在路網中的時空路徑,被廣泛應用于列車運行圖鋪畫研究中。本文在高鐵服務網的基礎上,引入時間維度,構建高鐵時空網(V,A′),其中V由物理點i∈N′擴展為時空頂點(i,t)∈V,表示列車在t時刻位于物理點i,A′由物理弧(i,j)∈A擴展為時空弧(i,j,t,s)∈A′,表示列車由頂點(i,t)移動到頂點(j,s),作業時間為s-t。服務網中各類物理弧可以擴展為以下5種時空弧:
為了更好地描述列車運行過程且保證模型的可行性,構建以下2種弧:
時空網中列車停站弧,列車跨線弧和列車運行弧的費用ci,j,t,s為實際作業時間,列車生成弧及列車到達弧的費用ci,j,t,s為0,列車虛擬運行弧的費用為無限大。基于圖1(b)的高鐵時空網中各類時空弧的構建以及不同速度等級的本線及跨線列車在時空網中的路徑選擇見圖2,同理可構建另一方向的時空弧。
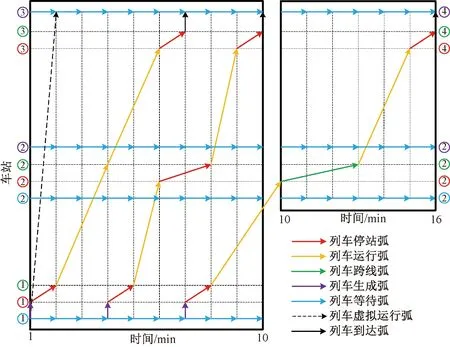
圖2 時空網的構建及列車的路徑選擇
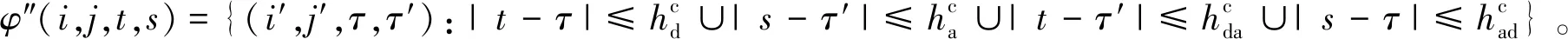
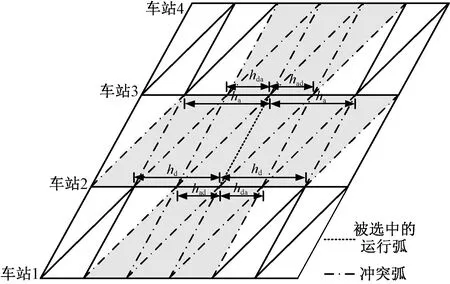
圖3 沖突弧集的構建
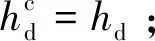
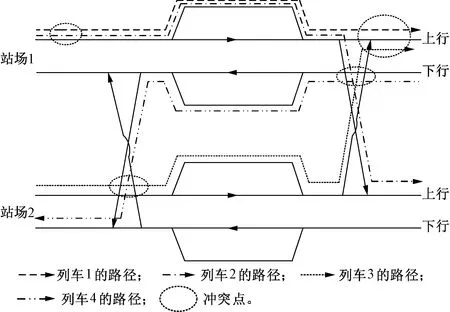
圖4 跨線站站場布局及列車進路

表2 列車在跨線站的最小列車間隔時間
2 模型構建
本節基于高鐵時空網構建鋪畫列車運行圖的整數規劃模型,模型的輸入為:①高鐵物理網;②列車開行方案;③基礎數據:如列車最大最小停站時間、各種最小列車間隔時間、列車在各區間的運行時間等。模型的輸出為:列車運行圖、通過能力。
模型的目標函數為最大化列車選擇運行弧的數量,即最大化列車開行數,即
( 1 )
為提高模型解的質量且方便算法求解,將式( 1 )轉換為
( 2 )
通過阻止列車選擇虛擬運行弧(即最小化列車選擇時空弧的總費用)來最大化列車開行數,同時還可以最小化列車運行費用。模型的約束條件為
( 3 )
( 4 )
Depmin(k)≤DT(k)≤Depmax(k)
( 5 )
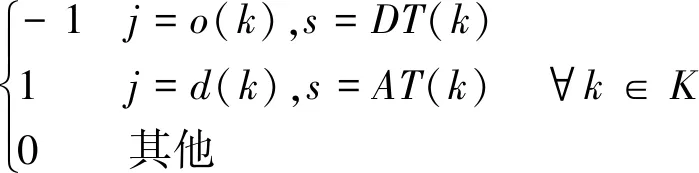
( 6 )
( 7 )
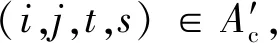
本文提出的模型為典型的NP-hard模型,復雜度較高。為直觀地展示模型規模,模型中變量和各約束的數量見表3,由于式( 3 )~式( 5 )可以歸并到式( 6 )中,因此式( 6 )和式( 7 )的數量見表3。

表3 模型規模
3 基于ADMM的分解算法
本文研究的列車運行圖鋪畫問題實質上是將有限的時空資源分配給不同列車的多商品流問題,當案例規模較小時,可以使用商業求解器,如CPLEX,直接求得精確解。但當研究案例很大時,商業求解器不能在有效時間內求得最優解,所以提出使用分解算法將原問題分解為若干獨立子問題進行求解。本文使用的ADMM分解算法是增廣拉格朗日松弛算法與塊坐標下降法的結合。其中,增廣拉格朗日松弛算法是在拉格朗日松弛算法的基礎上引入困難約束的二次懲罰項,可以提高模型的魯棒性,但是二次項的引入會使模型非線性化,需要結合使用塊坐標下降法處理該二次項,將運行圖鋪畫問題分解為單個列車的最短路問題。
模型中安全約束式( 7 )會引起列車的大規模組合,其他約束都只針對單個列車。將式( 7 )作為懲罰項放入目標函數式( 2 )中,新的目標函數為
( 8 )
式中:q為弧(i,j,t,s);ρ為二次項懲罰乘子;μq為拉格朗日懲罰乘子,其迭代方法為次梯度法,即
( 9 )
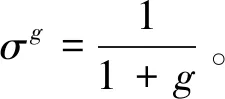
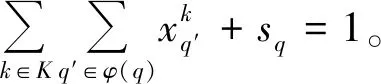
(10)
(11)
則二次懲罰項轉化為
(12)
其中當πk≥1時,二次懲罰項的推導過程為
(13)
代入目標函數式( 8 )中,通過合并同類項得到
(14)
式中:Q為一個常數。
新的費用更新為
(15)
最后,經過ADMM分解的模型變為:目標函數式(14),約束條件式( 6 )。可見新模型中各列車相互獨立,原問題可被分解為若干獨立的最短路子問題,各子問題可通過動態規劃求解。在每次迭代求解過程中依次為列車集合K={1,2,3,…,k,…,n}中的列車尋找最短路,n為k中列車的數量,當鋪畫列車k的運行線時,固定其他列車的決策變量解,以此循環。
基于ADMM分解算法的步驟為:
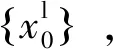
Step2通過動態規劃算法為每列車尋找最短路徑,用式(15)計算弧的費用,得到決策變量解集{xg}。
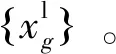
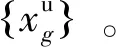
Step5使用式( 9 )更新拉格朗日乘子。
Step6如果迭代次數達到預先設定的最大迭代次數,結束算法,否則,返回Step2,g=g+1。
4 案例分析
以我國太原—德州高鐵和鄭州—北京高鐵路網為例,同時鋪畫生成兩條線路的本線及跨線列車運行圖,驗證模型及算法的可行性。提出的算法在Python平臺上實現,算法運行環境為一臺內存16 GB,CPU:i7-770HQ 2.80 GHz的臺式計算機。
太原—德州及鄭州—北京高鐵共設23個車站,兩條線路的交匯車站石家莊站為跨線站,10個方向的列車(太原—德州、德州—太原、鄭州—北京、北京—鄭州、太原—北京、北京—太原、太原—鄭州、鄭州—太原、鄭州—德州、德州—鄭州)在石家莊站可能會產生進路沖突,石家莊站的站場圖及各方向列車在石家莊站的列車徑路見圖5,不同方向列車在石家莊站的最小列車間隔時間見表4。根據現有列車運行圖,只有太原—德州、德州—太原、太原—北京、北京—太原方向有“D”字頭列車,其他方向列車均為“G”字頭列車,列車在各運行區段的運行時間見表5。設置案例的總時長為600 min,即時空網的時間跨度為600 min,離散化后的單位時間刻度為1 min。本文將跨線列車列入研究對象,為突出跨線列車的影響且精確量化跨線列車的開行比例,假設各列車的起點站和終點站都為太原、德州、北京和鄭州,所以各方向列車數量根據現有運行圖比例輸入為:太原—德州7列,德州—太原7列,太原—北京18列,北京—太原18列,太原—鄭州5列,鄭州—太原5列,鄭州—德州6列,德州—鄭州6列,鄭州—北京40列,北京—鄭州40列。設置各最小列車間隔時間ha=3 min,hd=3 min,had=2 min,hda=2 min。
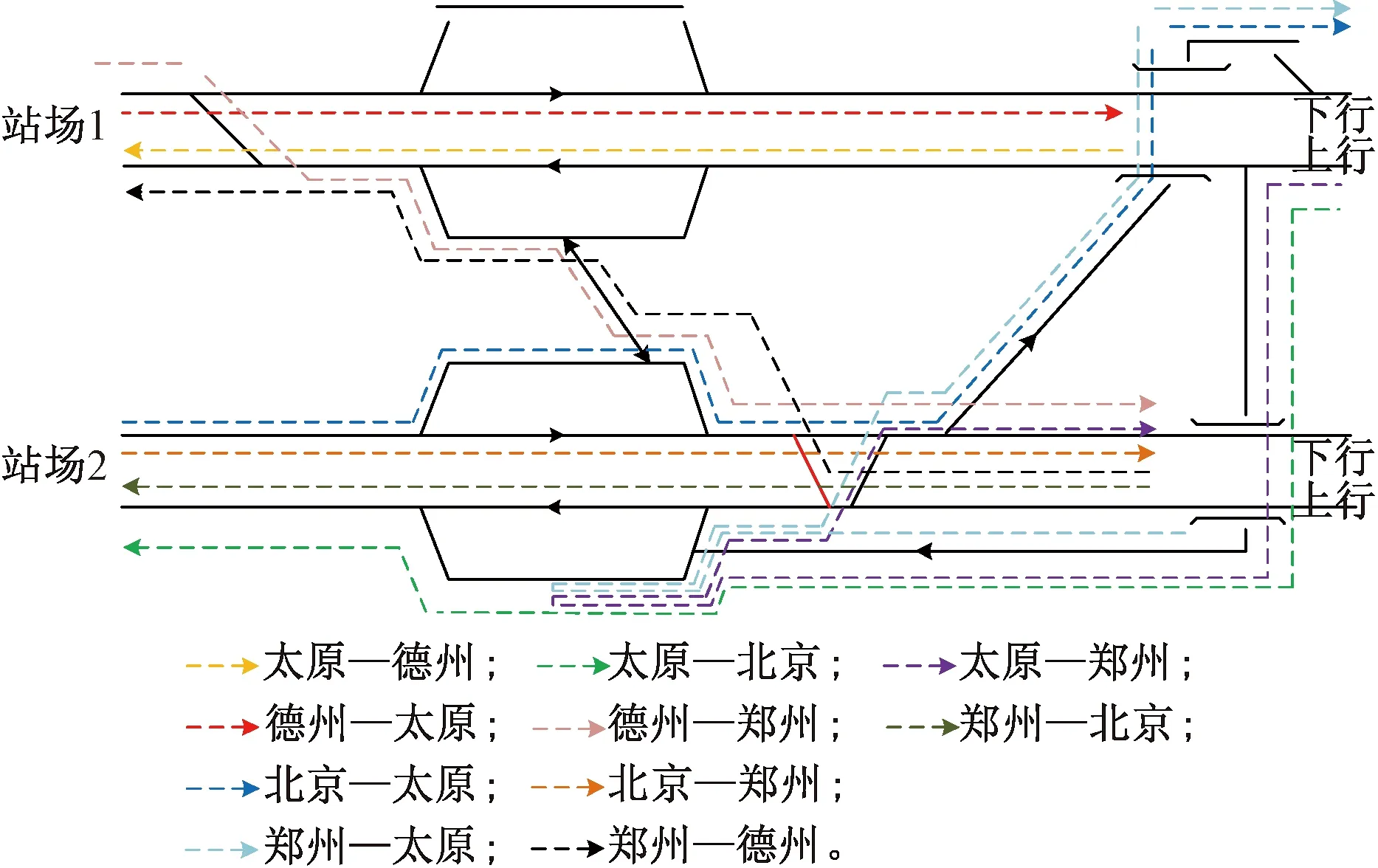
圖5 石家莊站站場圖及各方向列車徑路

表4 不同方向列車在石家莊站的最小列車間隔時間
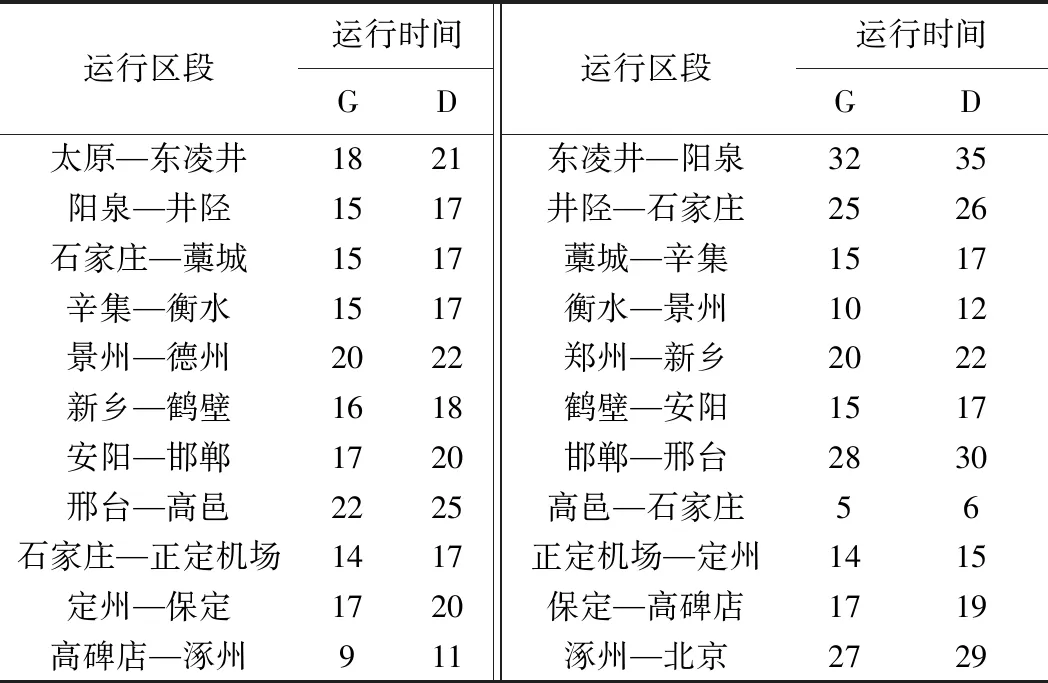
表5 列車在各運行區段的運行時間 min
4.1 計算結果與分析計算法的對比分析
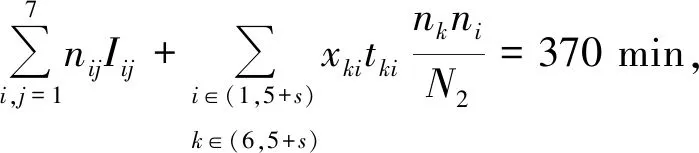
文獻[13]提出的通過能力計算方法是在已知列車開行方案和運行圖的前提下用來評估當下通過能力利用情況的一種方法,計算過程較本節更為簡單;而本文提出的通過能力計算方法則可根據需要,鋪畫出具有特定要求(如列車出發時間窗,跨線列車開行比例等)的飽和列車運行圖,根據在研究時段內最多可鋪畫的列車數量計算通過能力,是一種可視化的通過能力計算方法,兩種方法可根據需要互為補充。
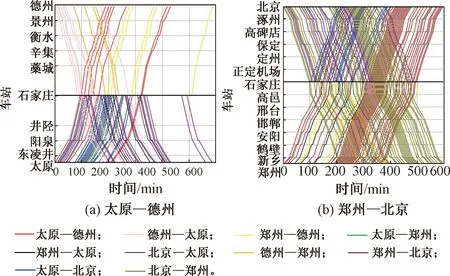
圖6 使用本文方法生成的高鐵運行圖
4.2 跨線列車比例對高鐵通過能力影響分析
為了更直觀的體現跨線列車對高鐵通過能力及運行圖的影響,研究不同跨線列車比例下不同的列車開行數量。輸入列車總數固定為152列,由圖6(b)可知,鄭州—北京能力已趨于飽和,所以通過刪除鄭州—北京方向與北京—鄭州方向列車,增加相應數量的跨線列車來調整跨線列車比例。圖7統計了當跨線列車占分別為38%、46%、54%、62%時,600 min內可鋪畫的列車總數為144、138、134、132列。由于跨線列車的增加,列車在跨線站的停站時間增加,且各方向列車在跨線站的互相干擾也隨之增多,造成了大量的能力消耗,可鋪畫列車數量降低。但從圖7也可以看出可鋪畫列車數量減小的速度在慢慢降低,其原因是隨著跨線列車的增多,具有相同屬性的列車也隨之增多,從而緩解了能力占用。由于跨線高鐵列車一般運程較長,較運程較短的本線列車可實現更高的經濟效益,因此在通過能力允許范圍內,通過合理調整列車結構,適當提高跨線列車比重,可以收到更優的運營效果。
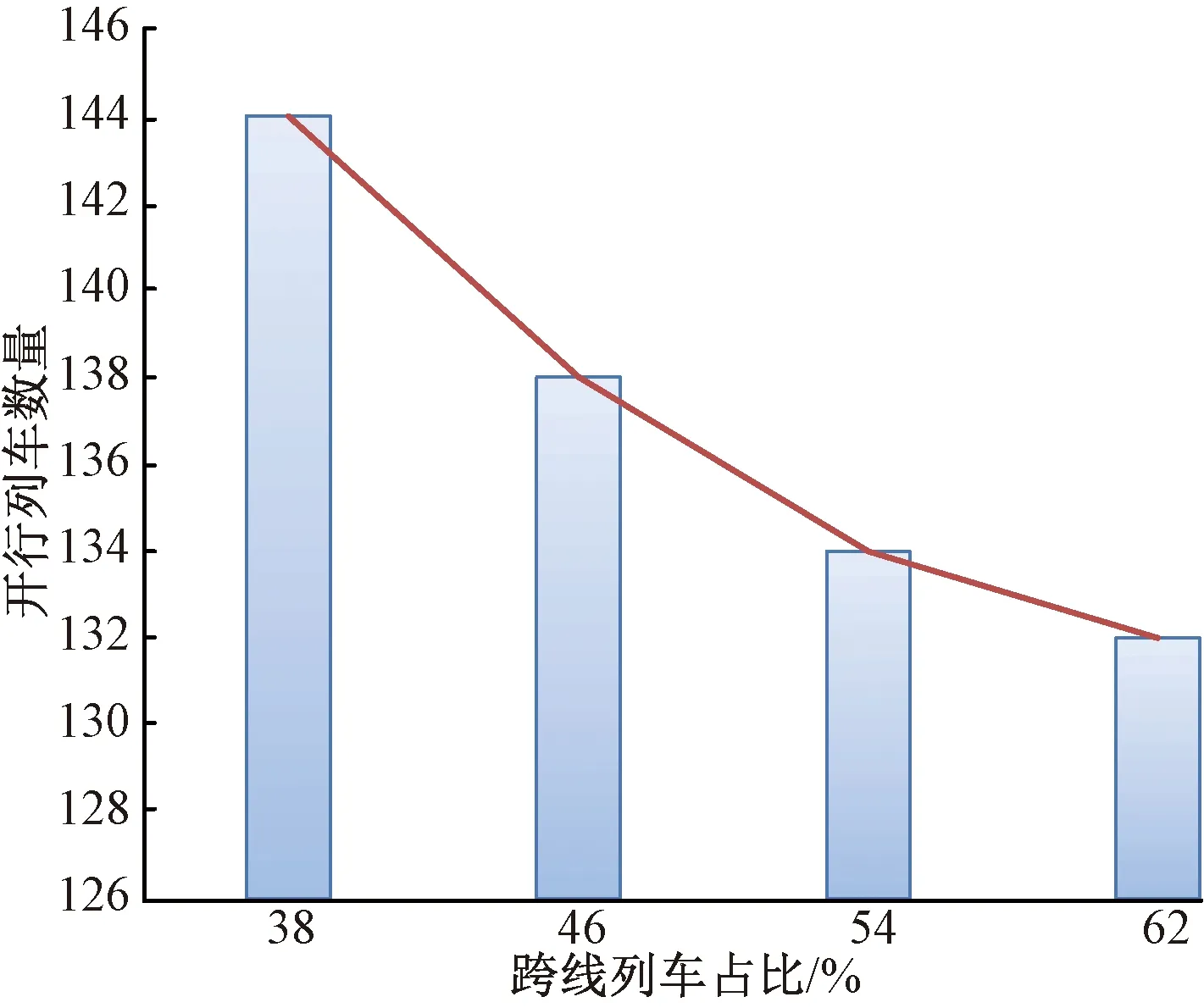
圖7 不同跨線列車比例下列車開行數量
4.3 車站站場布局對高鐵通過能力影響分析
本文提出的方法也可以評價高鐵站站場布局,見圖5,將圖中紅色道岔取消,鄭州—德州方向列車直接改用立交形式由站場1到達站場2,那么該方向列車與太原—鄭州、北京—太原、北京—鄭州,德州—鄭州和鄭州—太原方向的列車沒有沖突,計算結果見圖8,600 min內太原—德州和鄭州—北京高鐵可鋪畫列車數為150列,較圖6可多鋪畫6列列車,表明在跨線列車運行需求較大的繁忙高鐵干線,合理的高鐵站站場布局可減少列車進路沖突,從而提高高速鐵路通過能力。
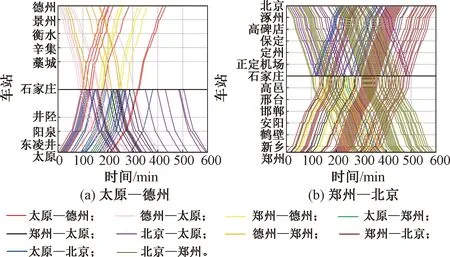
圖8 站場優化后的高鐵運行圖
5 結論
本文深入研究了高鐵樞紐內跨線列車運行對高鐵通過能力和運行圖鋪畫的影響機理。提出在跨線站不同方向列車之間的進路沖突可用最小列車間隔時間標準為判據,建立基于時空網絡的整數規劃模型,設計了ADMM分解算法將原問題分解為若干尋找單個列車的最短路徑問題,獲得了各方向列車運行線在跨線樞紐的最佳配合方案。并以太原—德州及鄭州—北京高鐵為例,驗證了方法的可行性。論文分析、評估了跨線列車占比變化和高鐵站站場布局優化對高速鐵路通過能力影響,為進一步提高高鐵運營效能提供了科學依據。

