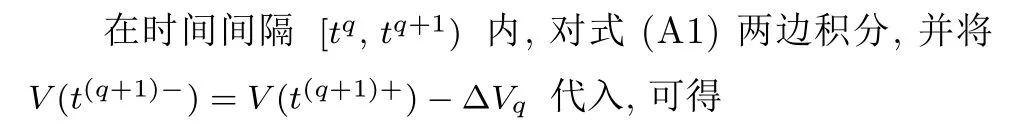具有間歇性執行器故障的非線性系統自適應CFB 控制

乃永強 楊清宇 周文興, 楊瑩

由于故障時刻,故障模式以及故障值完全不可預測,因此如何消除執行器故障對控制系統的影響已成為控制領域的技術難點[1].到目前為止,自適應控制[2?3]已成為解決執行器故障補償問題的有效策略.與其他控制方法相比,自適應補償控制具有如下的優點: 1) 能夠自動調節執行器故障引起的不確定性;2) 控制器利用自適應律可在線調整其估計參數;3) 當故障信息完全未知時,也可以獲得期望的控制目標.利用線性矩陣不等式技術,文獻[4?6]分別研究了線性系統執行器故障的自適應補償問題.文獻[7]提出的直接自適應控制方案解決了具有卡死 (Lock in place,LIP) 執行器故障和未知系統參數的線性系統的跟蹤控制問題.結合自適應Backstepping 控制技術,文獻[8?10]分別研究了具有LIP 故障的非線性系統的補償控制問題.文獻[11?12]解決了具有部分失效 (Partial loss of effectiveness,PLOE)和LIP 故障的非線性系統的跟蹤控制問題.文獻[13]解決了具有 PLOE 故障和LIP 故障以及松浮 (Float) 故障的非線性系統的跟蹤控制問題.由于NNs (Neural networks)或模糊邏輯系統的通用逼近特性,文獻[14?19]提出的自適應神經或模糊控制方案補償了執行器故障對系統的影響.然而,文獻[4?19]僅僅解決了一次性執行器故障的補償問題,即所有執行器的狀態在故障發生之后保持不變.雖然在故障時刻存在未知參數的跳變,但未知參數的跳變次數和Lyapunov 函數有界,因此可以保證閉環系統的穩定性和期望的跟蹤指標.

在實際應用中,控制系統的執行器在運行過程中也經常發生各種不可預測的間歇性故障.即執行器的狀態在正常運行和故障之間（或者各種故障之間）進行頻繁地切換.正如文獻[20]所指出的,間歇性執行器故障會不可避免地導致系統中未知參數的間歇性跳變,并且跳變的總次數可趨于無窮大.因此,一次性故障的研究成果[4?19]不能直接用于具有間歇性執行器故障的控制系統的補償控制中,主要有如下的原因: 1) 隨著跳變次數的不斷累積,控制器中的一些估計參數會不斷的增加,最終當跳變次數趨于無窮大時,這些估計參數將變得無界;2) 由于存在未知參數的間歇性跳變,則包含參數估計誤差的 Lyapunov 函數在每個跳變時刻必將產生一個跳變幅度.從而上述 Lyapunov 函數的可能增加隨著跳變次數的增加而不斷累積,最終當跳變次數趨于無窮大時,閉環系統的穩定性將得不到保證.因此,在間歇性執行器故障的自適應補償控制方案設計中,如何有效地保證參數估計的有界性以及閉環系統的穩定性是執行器故障補償領域的一個技術難點.

目前關于非線性系統的間歇性執行器故障補償控制的研究成果還非常有限.在文獻[20]中,Wang等首次解決了一類參數化嚴格反饋非線性系統的間歇性執行器故障的補償問題.所設計的自適應模塊化控制方案保證了所有閉環信號的有界性.但是,該方案僅僅保證了均方意義上的跟蹤誤差的有界性.從而不能建立跟蹤誤差與設計參數之間的明確關系.受文獻[20]的啟發,Lai等[21?22]和Xing等[23]進一步研究了非線性系統間歇性執行器故障的補償問題.文獻[24]解決了含有未知時滯非線性系統的間歇性執行器故障的補償問題.文獻[25]解決了航天器姿態控制系統間歇性執行器故障的補償問題.采用K?濾波器技術[26?27],兩種自適應輸出反饋控制方案補償了間歇性執行器故障的影響[28?29].但是,以上方案[20?25, 28?29]僅僅證明了系統的穩定性和穩態跟蹤指標,沒有建立跟蹤誤差意義下的系統暫態指標與設計參數之間的關系.從而不能通過調節設計參數改善系統的暫態指標.在文獻[22]中,作者在假設故障次數有限的前提下,提出了一種暫態跟蹤誤差指標的顯式界.但是該界取決于系統中故障的次數.當故障次數趨于無窮大時,系統的暫態指標不能被保證.則文獻[22]中建立的系統暫態指標不能應用于考慮無限次故障的暫態指標分析中.因此,在間歇性執行器故障的情況下,所設計的補償控制方案中如何明確地建立跟蹤誤差意義下的系統暫態指標與設計參數之間的關系并通過調節設計參數獲得良好的系統暫態指標也具有重要的理論與工程意義.

此外,文獻[9?13,20?23,28?29]設計的基于傳統的 Backstepping 故障補償控制方案需要對虛擬控制律的偏導數進行解析計算.如文獻[30?31]所述,隨著系統階數的增加,上述計算將變得非常復雜,從而限制了上述方案在實際中的應用.鑒于此,文獻[30?31]提出的CFB 控制技術在不滿足匹配條件的非線性系統的自適應控制中引起了廣泛的關注.與傳統的Backstepping 技術相比,CFB 方法有如下的優點: 1) 指令濾波器可精確地估計虛擬控制信號及其導數;2) 消除了虛擬控制律解析微分的計算,使得控制律的設計更容易實現;3) 指令濾波器引起的濾波誤差在控制器中得到了補償.因此,本文采用 CFB 控制技術,針對一類不確定嚴格反饋非線性系統,提出一種自適應控制方案以解決間歇性執行器故障的補償問題.

本文的主要貢獻如下:

1) 采用投影算子在線調整控制器中的估計參數,可消除故障次數不斷累積而導致的估計參數值不斷增加的問題.

2) 改進的Lyapunov 函數證明了所提出的方案能夠保證所有閉環信號的有界性.同時明確地建立了跟蹤誤差與Lyapunov 函數的跳變幅度,最小故障時間間隔和設計參數之間的關系.特別是,Lyapunov 函數的跳變幅度越小和兩個連續故障之間的時間間隔越長,系統跟蹤指標越好.應該指出的是,系統的跟蹤指標與故障次數無任何關系.

3) 通過迭代計算建立了暫態跟蹤誤差指標的均方根型界.該界說明了通過選擇恰當的設計參數,可獲得良好的跟蹤誤差意義下的系統暫態指標.需要說明的是,該均方根型界不依賴于故障的總次數.

本文其余部分安排如下: 第 1 節給出了問題的描述.第 2 節設計了控制方案.第 3 節進行了仿真研究.第 4 節總結了全文并給出了進一步的研究工作.

1 問題描述

1.1 非線性系統

考慮如下不確定嚴格反饋非線性系統

2) 便于第 2 節的控制器設計以及穩定性分析,給出如下的定義.在時間區間 [tq,tq+1) (q∈N+)內,假定有mq(mq ≤m ?1) 個執行器k1,···,kmq發生 LIP 故障,且在未知時刻tq+1之前,所有執行器的狀態不發生變化.

控制的目標是設計一種自適應控制方案使得:a) 能夠有效地補償未知間歇性執性行器故障對系統的影響;b) 閉環系統中所有信號的有界性被保證;c) 系統的輸出y∈R 可跟蹤期望輸出yd∈R,其中yd和y˙d已知且有界;4) 通過選擇恰當的設計參數,可調節系統在跟蹤誤差意義下的穩態和暫態指標.

為了實現上述控制目標,需要如下的假設.

假設 1.在每個時間間隔 [tq,tq+1) 內,當任意不大于m ?1 個執行器發生LIP 故障時,剩余的執行器仍可驅動系統完成上述控制目標.

注 2.假設 1 是保證系統 (1) 可控性的基本且必要的假設.在每個時間間隔 [tq,tq+1) 內允許所有執行器同時發生 PLOE 故障.但是當所有執行器同時發生 LIP 故障時,則不能完成上述控制目標.假設 1 還表明了每個執行器存在無限次故障的可能性.假設 2[30]表明了非線性函數fi(·),gi(·),bk(·)在x∈Rn上滿足 Lipschitz 條件.因此,對于任意的x(0)∈Rn,系統 (1) 都存在唯一的連續解x(t)[32].從而系統 (1) 定義的初值問題的解x(t) 的有界性在?t∈[0,∞) 上被保證.假設 3 表明了故障參數的 有界性以及上的變化率的有界性.已知常數和將用于第2.2節的自適應律設計中.此外,假設和上均為光滑函數僅僅是為了第 2.3 節的穩定性分析的目的,不用于控制器的設計中.

1.2 極限學習機的學習理論

極限學習機 (Extreme learning machine,ELM) 是由 Huang等[33]提出的用于單隱層前饋NNs 的快速學習算法,其本質上是一種單隱層前饋NNs.ELM 特點是隨機選擇網絡隱含層節點參數,在學習過程中僅需要調節網絡的輸出權值.正如文獻[34]所指出的,ELM 不僅提高了單隱層前饋NNs 的學習效率,而且完全保留了傳統單隱層前饋NNs 固有的通用逼近能力.根據文獻[34]中的定理II.1,對于任意的隨機函數序列,ELM可以逼近任意連續函數f(Z):Rn →R:

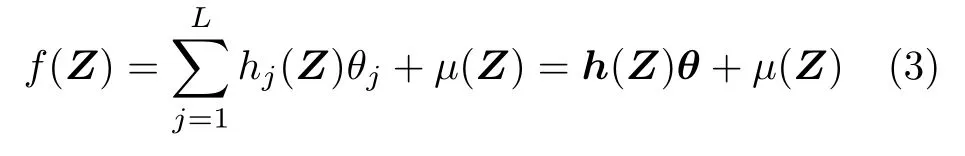
其中,Z∈SZ且SZ∈Rn表示緊集合;μ(Z) 表示逼近誤差并且存在未知常數0,使得|μ(Z);激活函數hj(Z) 可表示為

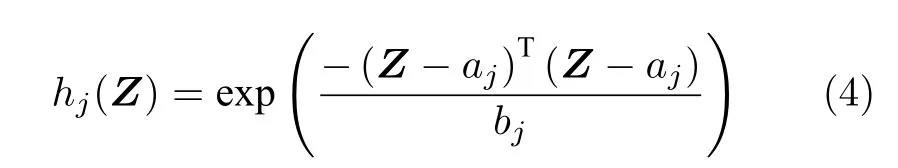
其中,j=1,···,L以及 (aj,bj) 表示第j個隱層節點的學習參數,其在 Rn×R+的任意區間上隨機選擇;θ=[θ1,···,θL]T∈RL表示 ELM 的最優權值,其真實值未知.因此,在第 2.1 節的控制器設計中,采用了基于估計的逼近模型

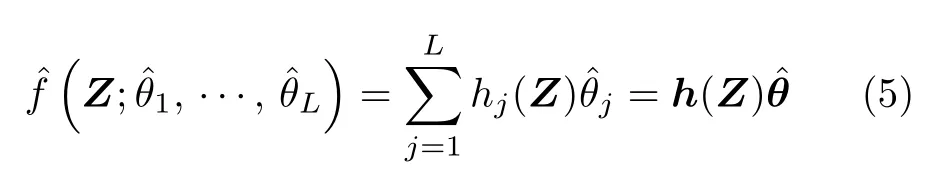
使得對于?Z∈SZ,逼近誤差μ最小.緊集合定義為

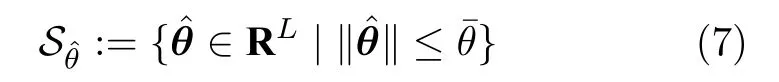
2 自適應神經補償控制設計

首先,針對具有間歇性執行器故障 (2) 的系統(1),設計一種自適應 CFB 補償控制方案,并采用投影算子實時在線更新控制器中的估計參數使得參數估計的有界性被保證.圖1 給出了該控制方案的控制流程.在圖1 中,以i=3 為例,α2表示指令濾波器 (11) 的輸入,xc3和表示指令濾波器 (11)的輸出,也表示虛擬控制律α2及其導數的估計,信號α2,xc3,ξ3通過積分運算生成指令濾波誤差補償信號ξ2.其次,考慮到未知故障參數的間歇性跳變對系統穩定性的影響,定理 1 提出一種改進的Lyapunov 函數分析了閉環系統的穩定性.證明了所提出的補償控制方案能夠保證所有閉環信號的有界性.同時明確地建立了跟蹤誤差與Lyapunov 函數跳變幅度,最小故障時間間隔,設計參數之間的關系.最后,定理 2 利用迭代計算建立了暫態跟蹤誤差指標的均方根型界,該界表明了通過選擇恰當的設計參數,可獲得良好的跟蹤誤差意義下的系統暫態指標.

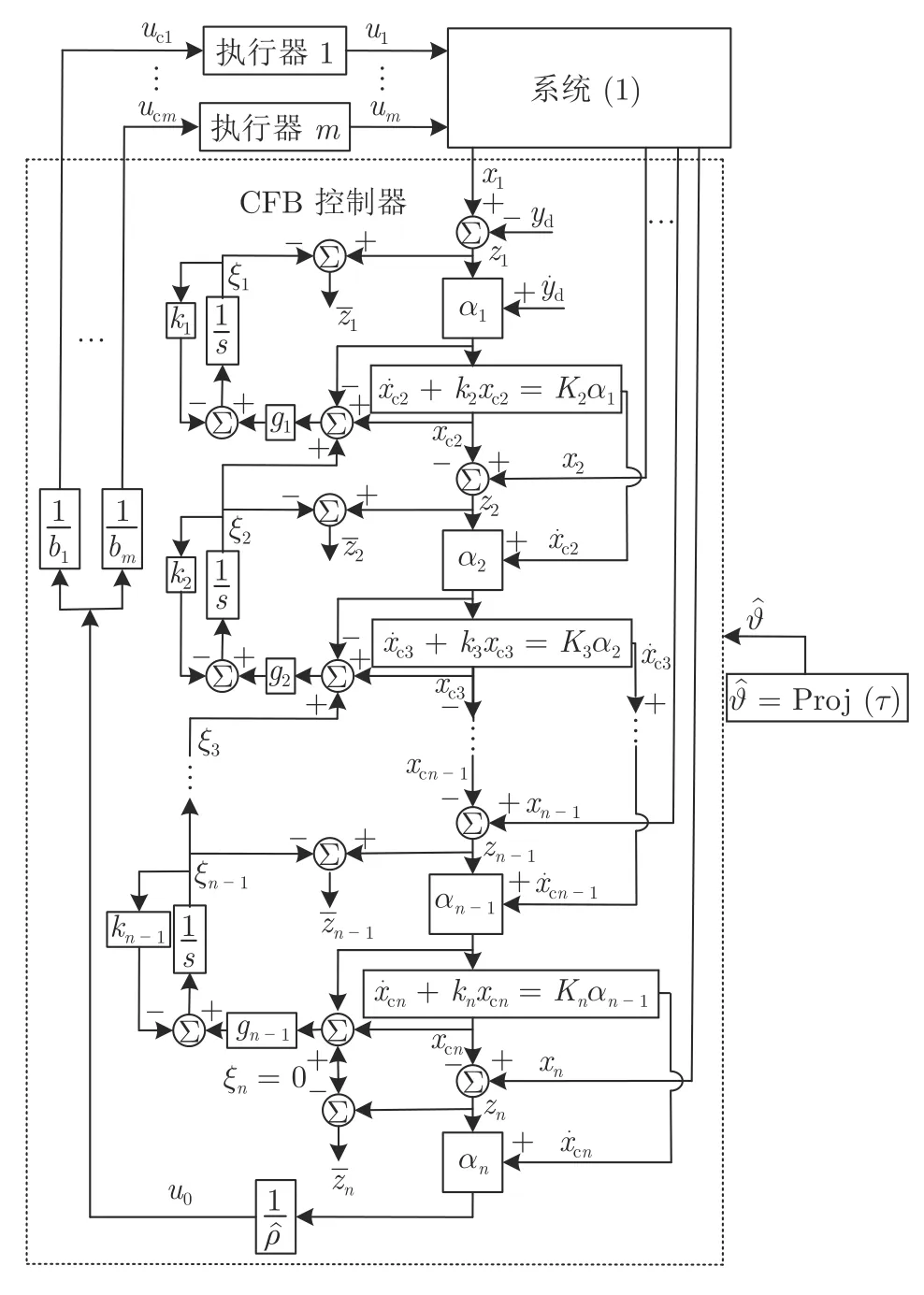
圖1 控制結構圖 (xci和 ,i =2,···,n,為濾波器(11) 的輸出.αi ,i =1,···,n,為式 (12)～(14) 中定義的虛擬控制律.ξi ,i =1,···,n ?1 為式 (17) 中定義的濾波誤差補償信號)Fig.1 Control block diagram (xci and fori=2,···,n are the outputs of the filter (11).αi fori=1,···,n is virtual control law defined in (12)～(14).ξi fori =1,···,n ?1 is the compensating signal of the filtered error defined in (17))

2.1 故障補償控制器設計

實際控制律設計為

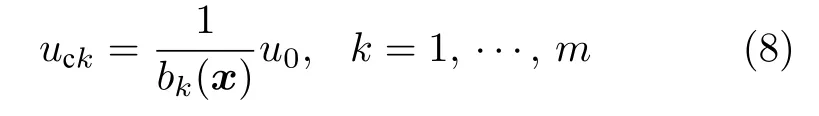
其中,u0將采用CFB 控制技術進行設計.利用注2 中的 2),并將式 (2)和式 (8) 代入系統 (1) 的第n個方程,有

其中,xc1=yd且yd為期望軌跡.由圖1 可知,當i=2,···,n時,xci與其時間導數由如下的指令濾波器[30?31]生成

2.2 自適應律設計

根據假設1,有如下的結論:

注 4.引理1 表明了對于?t∈[0,∞),投影算子(23)可明確地保證估計參數的有界性.從而消除了故障次數不斷累積而導致的控制器中估計參數不斷增加的問題.由于,?t∈[0,∞),則有如下的結論: 1)保證了參數估計誤差的有界性;2) 保證了由未知參數?間歇性跳變引起的所有Lyapunov 函數的跳變幅度的有界性.結論1)和2)將應用于定理1 的證明中.

2.3 穩定性分析

閉環系統的穩定性分析由定理1 給出.

定理 1.考慮由具有間歇性執行器故障 (2) 的不確定嚴格反饋非線性系統 (1),實際控制律 (8)和(15),虛擬控制律 (12)～(14),濾波器 (11)和(17) 以及基于投影算子的參數自適應律 (19) 組成的閉環系統.令系統的所有初始條件均有界并滿足假設 1～3 以及選擇恰當的設計參數.即使在運行過程中存在未知參數的間歇性跳變,所提出的控制方案能夠保證閉環系統所有信號的有界性.

證明.在每個時間間隔 [tq,tq+1) 內,Lyapunov 函數選擇為

2.4 暫態指標分析

3 仿真研究

選擇4 個實例為被控對象分別進行仿真實驗,以驗證所設計的自適應補償控制方案對間歇性執行器故障的補償能力和跟蹤控制指標.

3.1 實驗1: 數值仿真1

考慮如下的三階嚴格反饋非線性系統

其中,j=1,3,···;T?=20 s.從式 (44)和式 (45)中可看出,在每個jT?s 時間段內,系統中第1 個執行器的輸出將損失其有效性的 40%～80%,而第2 個執行器將鎖死在u2=8+4 cos(8t).在其余時間段內,兩個執行器均運行在無故障情況下.

首先,從圖2 (a) 可看出,系統的輸出y可跟蹤給定的期望輸出yd.從圖2 (b) 可看出,跟蹤誤差可漸近地收斂到零的一個很小的領域內,并且增加控制增益參數k1,k2,k3和自適應律因子Γ可獲得很小的跟蹤誤差.其次,圖3～5 分別表明了控制輸入信號u1,u2,濾波信號xc2,xc3,ξ1,ξ2和估計參數的有界性.從圖5(c)～5(f) 中可清楚地看出,動態參數隨著執行器狀態的不斷切換而不斷跳變.但是,選擇投影算子實時在線更新控制器中的估計參數,使得的有界性可得到明確地保證.最后,從圖2～5 中可看出,在均勻間隔周期執行器故障的情況下,所提出的補償控制器能夠驅動系統完成預期的跟蹤控制指標,同時保證了閉環系統中所有信號的有界性.

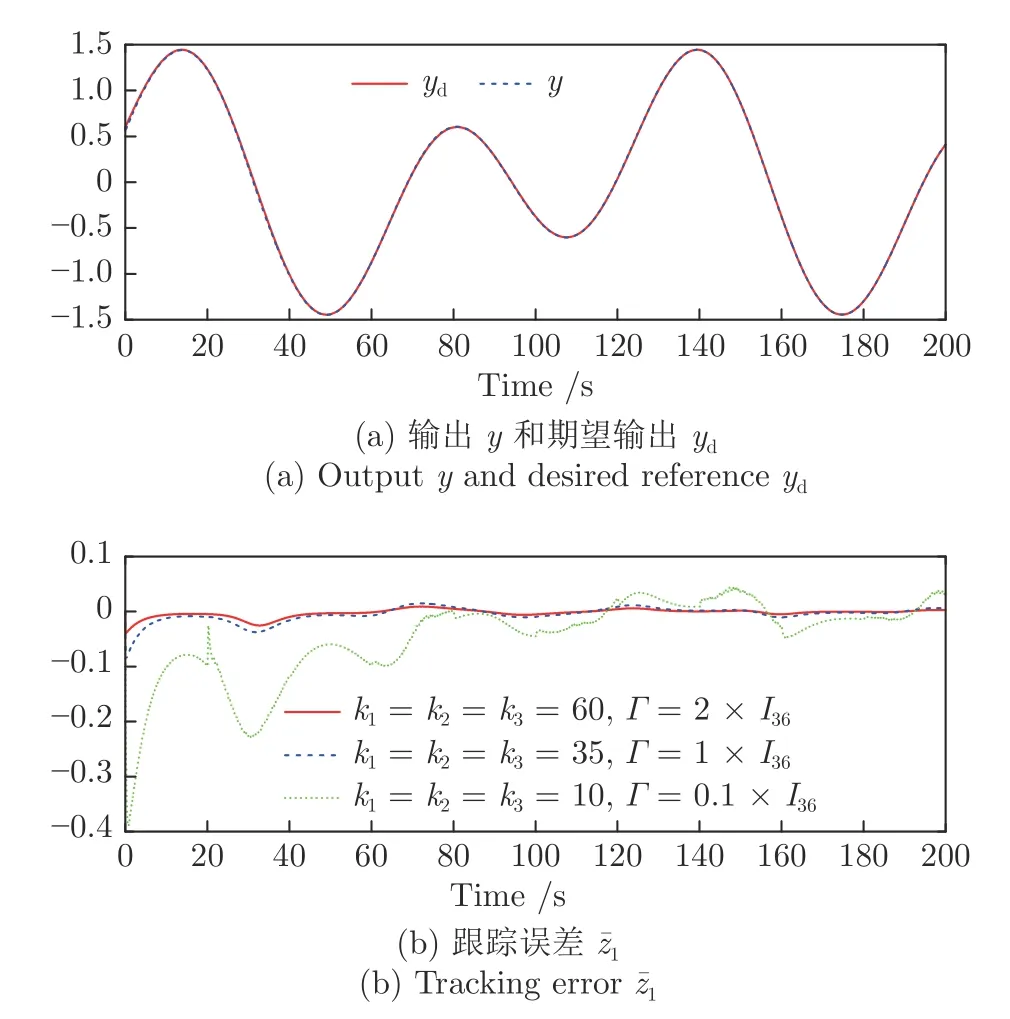
圖2 實驗1 中輸出y,期望軌跡yd 及跟蹤誤差Fig.2 Outputy,desired trajectoryyd and tracking error in Experiment 1

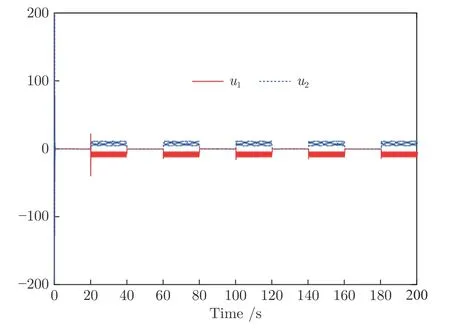
圖3 實驗1 中控制輸入u1和u2Fig.3 Control inputsu1 andu2 in Experiment 1

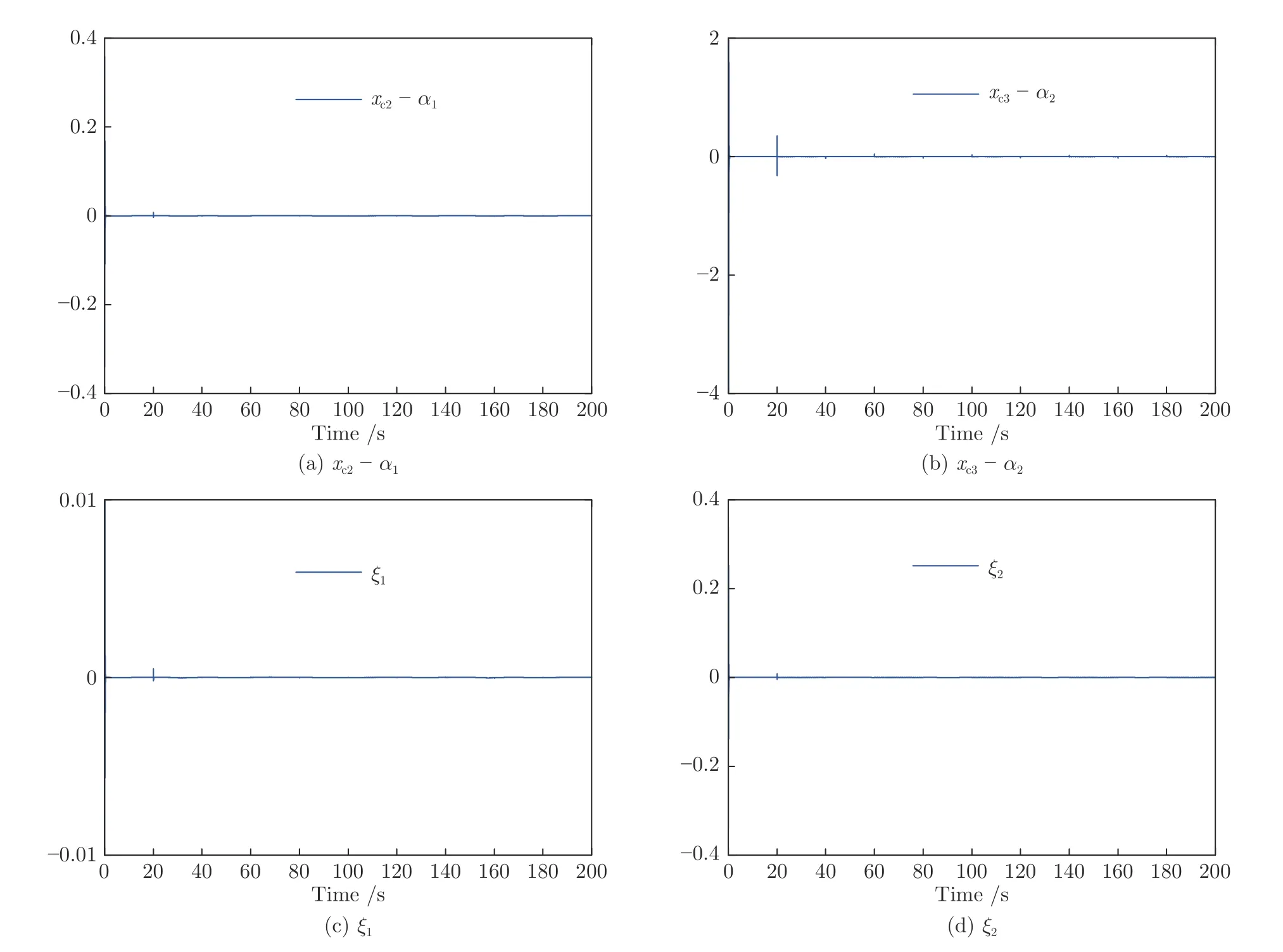
圖4 實驗1 中命令濾波誤差及其補償信號Fig.4 Command filtered errors and their compensating signals in Experiment 1

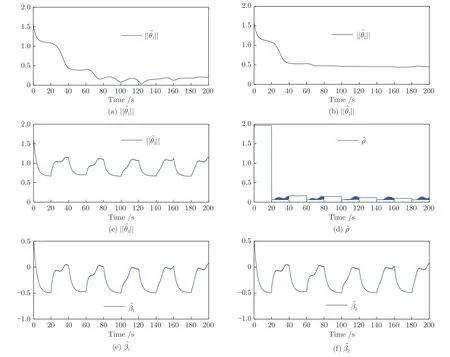
圖5 實驗1 中自適應參數Fig.5 Adaptive parameter in Experiment 1

3.2 實驗2: 數值仿真2

選擇如下的三階不確定嚴格反饋非線性系統

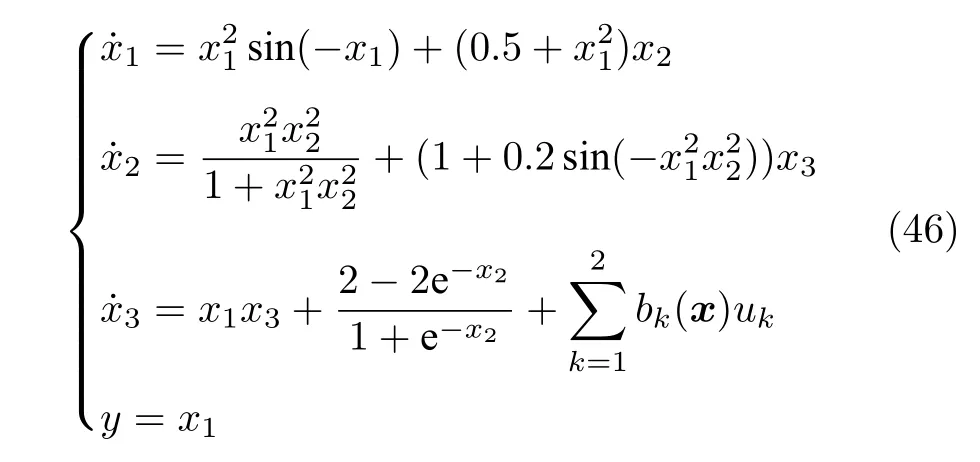
其中,b1(x)=b2(x)=2+sin(x1x2x3).

執行器故障模型選擇為

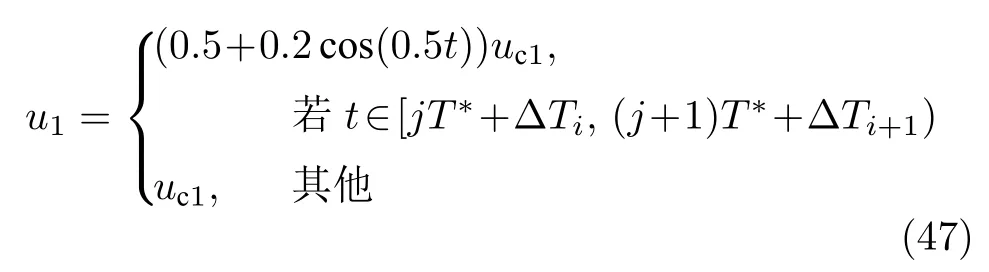
首先,圖6(a) 表明了系統的輸出y可跟蹤給定的期望輸出yd.圖6(b) 表明了跟蹤誤差可漸近地收斂到零的一個很小的領域內,并且增加控制增益參數k1,k2,k3和自適應律因子Γ可獲得很小的跟蹤誤差.其次,圖7～9 分別表明了控制輸入信號u1,u2,濾波信號xc2,xc3,ξ1,ξ2和估計參數的有界性.從圖9(c),9(e)和9(f) 中可清楚地看出,動態參數隨著故障參數跳變次數的增加而不斷跳變.但是,基于投影算子的參數自適應律可以保證的有界性.最后,從圖6～9 中可看出,在非均勻間隔周期執行器故障的情況下,所提出的自適應補償控制器不僅成功地驅動系統完成預期的跟蹤控制指標,而且保證了所有閉環信號的有界性.

圖6 實驗2 中輸出y,期望軌跡yd 及跟蹤誤差Fig.6 Outputy,desired trajectoryyd and tracking error in Experiment 2

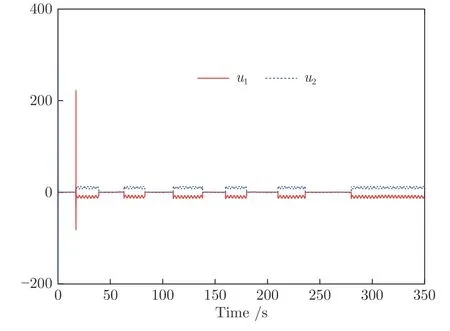
圖7 實驗2 中控制輸入u1和u2Fig.7 Control inputsu1 andu2 in Experiment 2

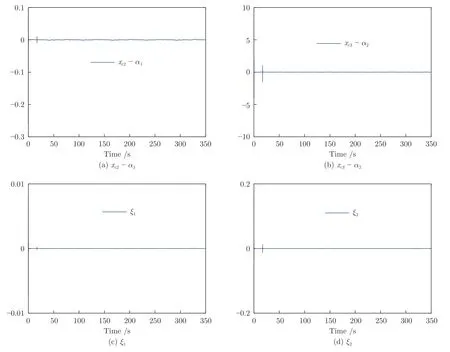
圖8 實驗2 中命令濾波誤差及其補償信號Fig.8 Command filtered errors and their compensating signals in Experiment 2

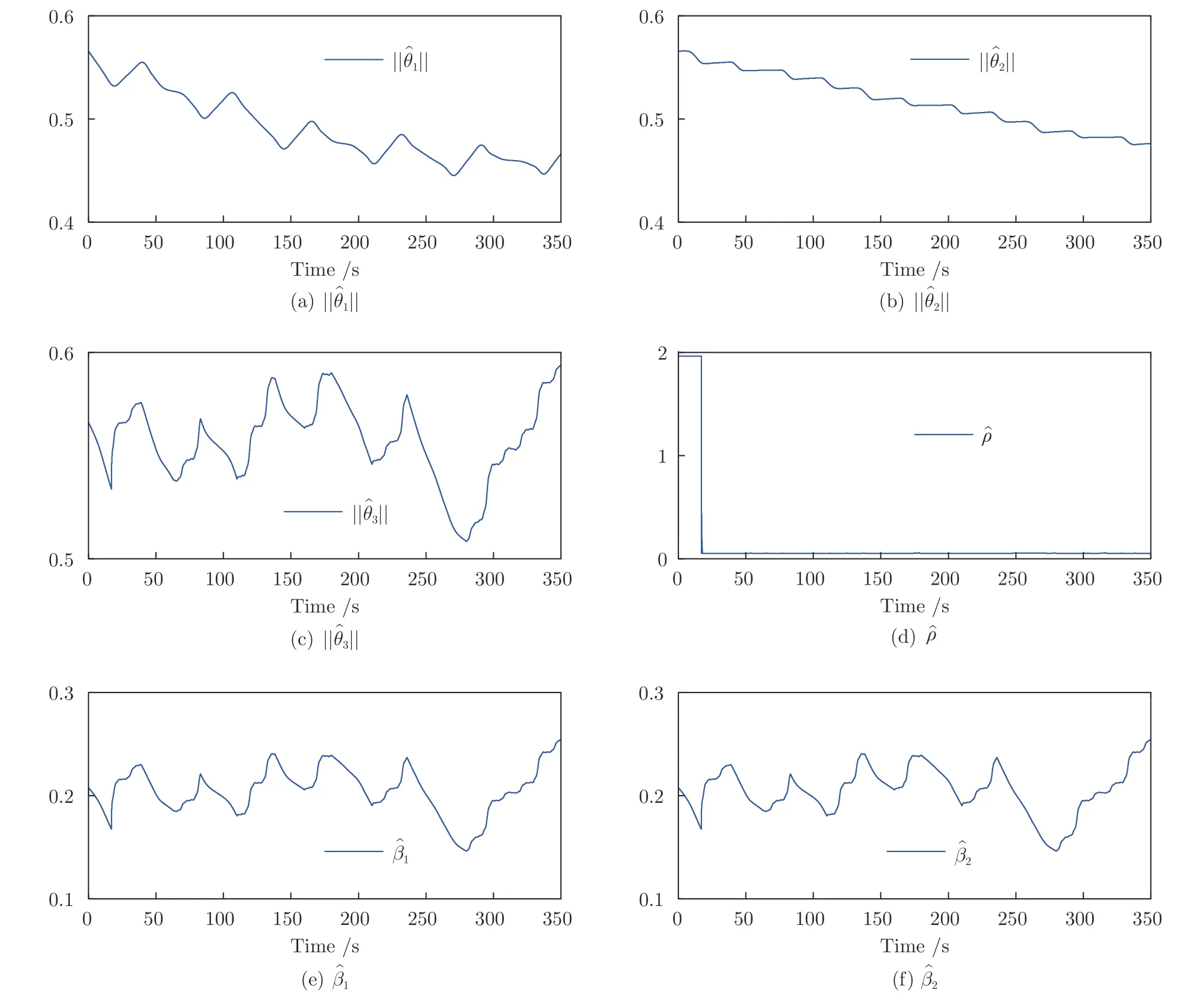
圖9 實驗2 中自適應參數Fig.9 Adaptive parameters in Experiment 2

3.3 實驗3: 三階單關節機器人的控制應用

將所提出的控制方案應用于實際的三階單關節機器人控制系統[36]中,以驗證其對間歇性執行器故障的補償能力.三階單關節機器人的動態方程為

其中,b1=b2=1/M. 在仿真中,系統參數選擇為D=B=1,M=0.05,Km=10,J=0.5和N=10.

執行器故障模型選擇為

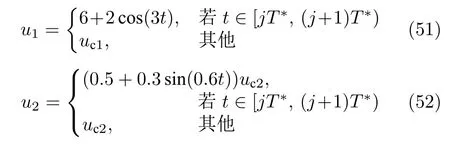
其中,j=1,3,···;T=15.從式 (51)和式 (52) 中可看出,在每個jT?s 時間段內,系統中第1 個執行器將鎖死在 6 +2 cos(3t),而第2 個執行器的輸出將損失其有效性的 20%～80%,在其余的時間段內,兩個執行器均運行在無故障情況下.

3.4 實驗4: 柔性機器人的控制應用

將所提出的控制方案應用于實際的柔性機器人控制系統[36]中,以驗證其對間歇性執行器故障的補償能力.柔性機器人的動態方程可表示為

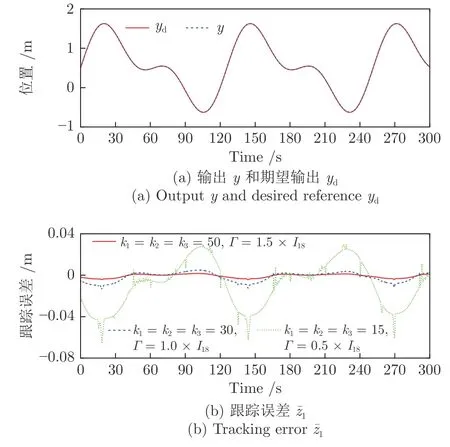
圖10 實驗3 中輸出y,期望軌跡yd 及跟蹤誤差Fig.10 Outputy,desired trajectoryyd and tracking error in Experiment 3

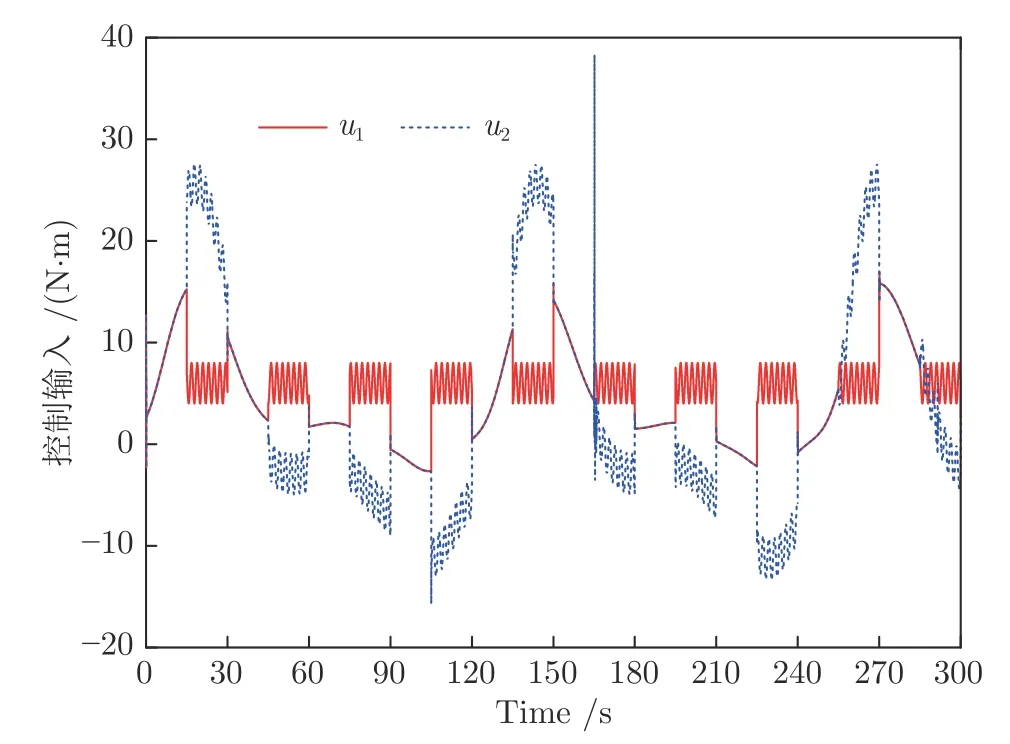
圖11 實驗3 中控制輸入u1和u2Fig.11 Control inputsu1 andu2 in Experiment 3

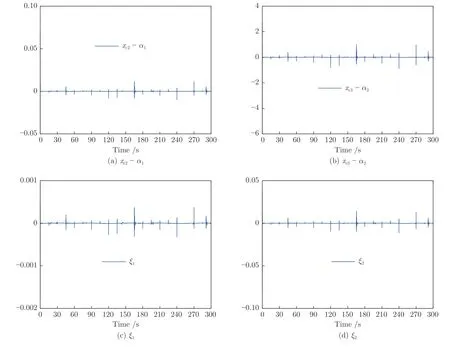
圖12 實驗3 中命令濾波誤差及其補償信號Fig.12 Command filtered errors and their compensating signals in Experiment 3

其中,b1=b2=1/J.在仿真中,系統參數選擇為M=2.3,L=1,g=9.8,I=ML2,J=0.5,K=15.

執行器故障模型選擇為

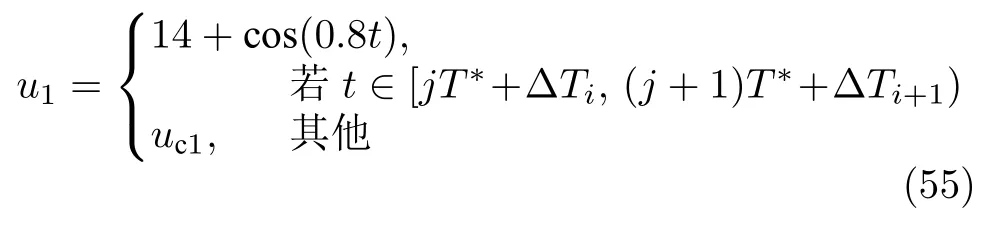
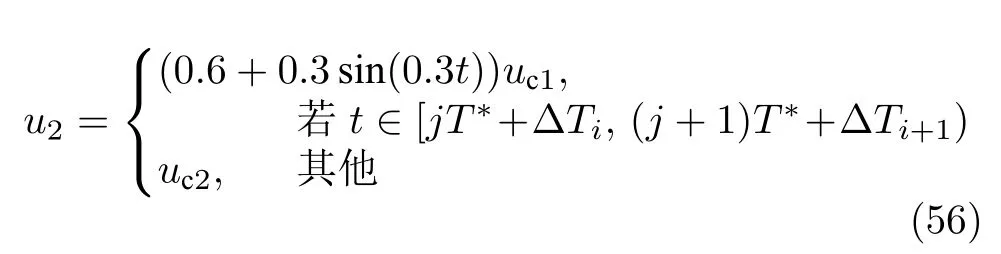
其中,j=1,3,···;T=25.在式 (55)和式 (56)中,加入不等間隔的 0≤?T1

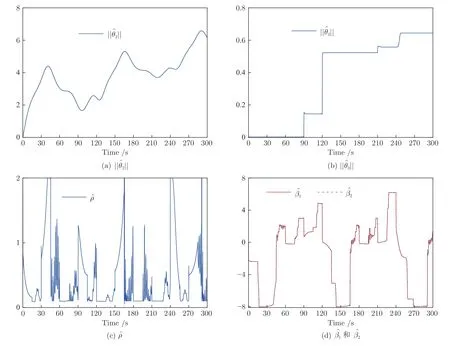
圖13 實驗3 中自適應參數Fig.13 Adaptive parameters in Experiment 3

首先,圖14(a) 顯示了系統的輸出y可收斂到其期望輸出yd的一個很小的領域內.從圖14(b)可看出,跟蹤誤差可漸近地收斂到零的一個很小的領域內.控制增益參數k1,k2,k3,k4和自適應律因子Γ越大,跟蹤誤差越小,即系統的暫態和穩態指標越好.其次,控制輸入信號u1,u2,濾波信號xc2,xc3,xc4,ξ1,ξ2,ξ3和估計參數有界性如圖15～17 所示.特別是圖17 (a)和圖17(b) 顯示了估計參數隨著參數跳變次數的增加而不斷增加.但是,基于投影算子的自適應律能夠明確保證的有界性.最后,從圖14～17 中可看出,在非均勻間隔周期執行器故障的情況下,所提出的補償控制器不僅能夠驅動系統完成預期的跟蹤控制指標,而且保證了所有閉環信號的有界性.

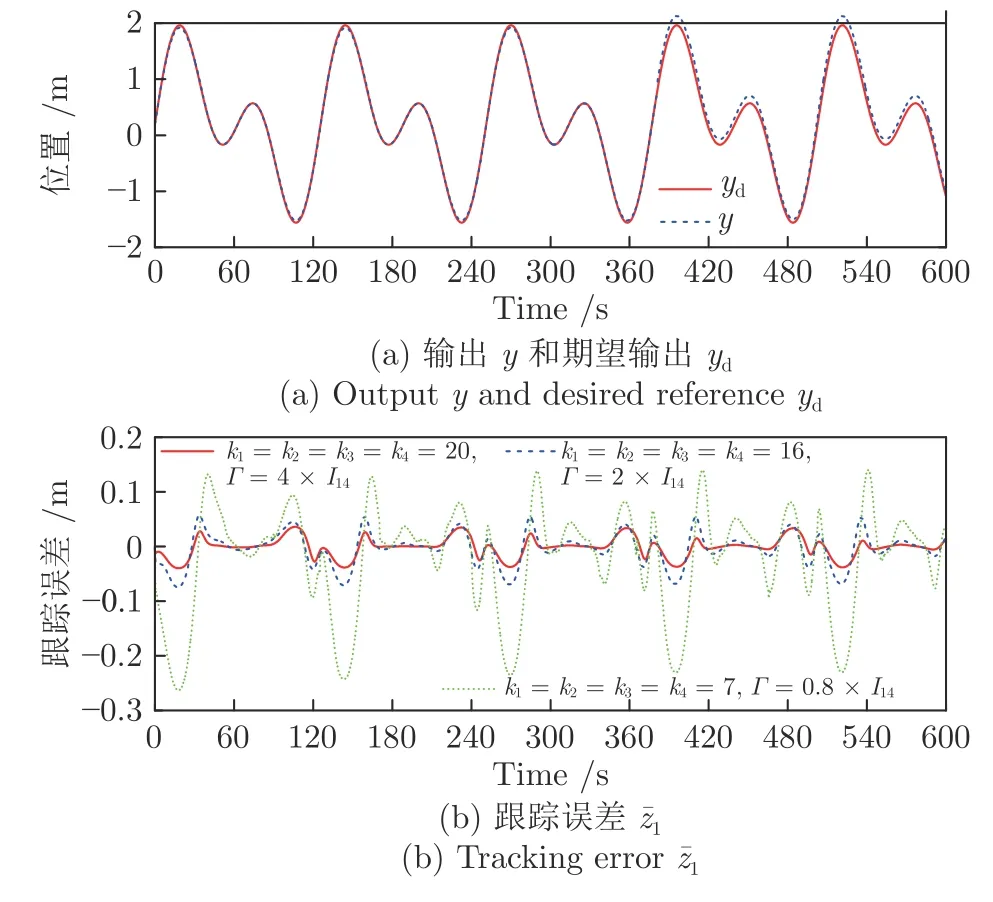
圖14 實驗4 中輸出y ,期望軌跡yd 及跟蹤誤差Fig.14 Outputy,desired trajectoryyd and tracking error in Experiment 4

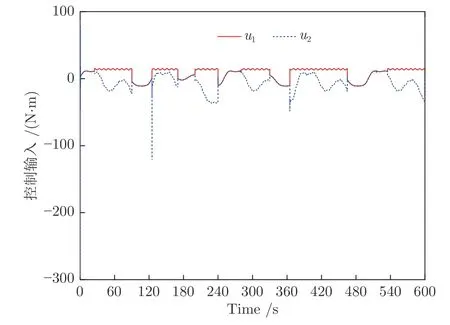
圖15 實驗4 中控制輸入u1和u2Fig.15 Control inputsu1 andu2 in Experiment 4

圖16 實驗4 中命令濾波誤差及其補償信號Fig.16 Command filtered errors and their compensating signals in Experiment 4

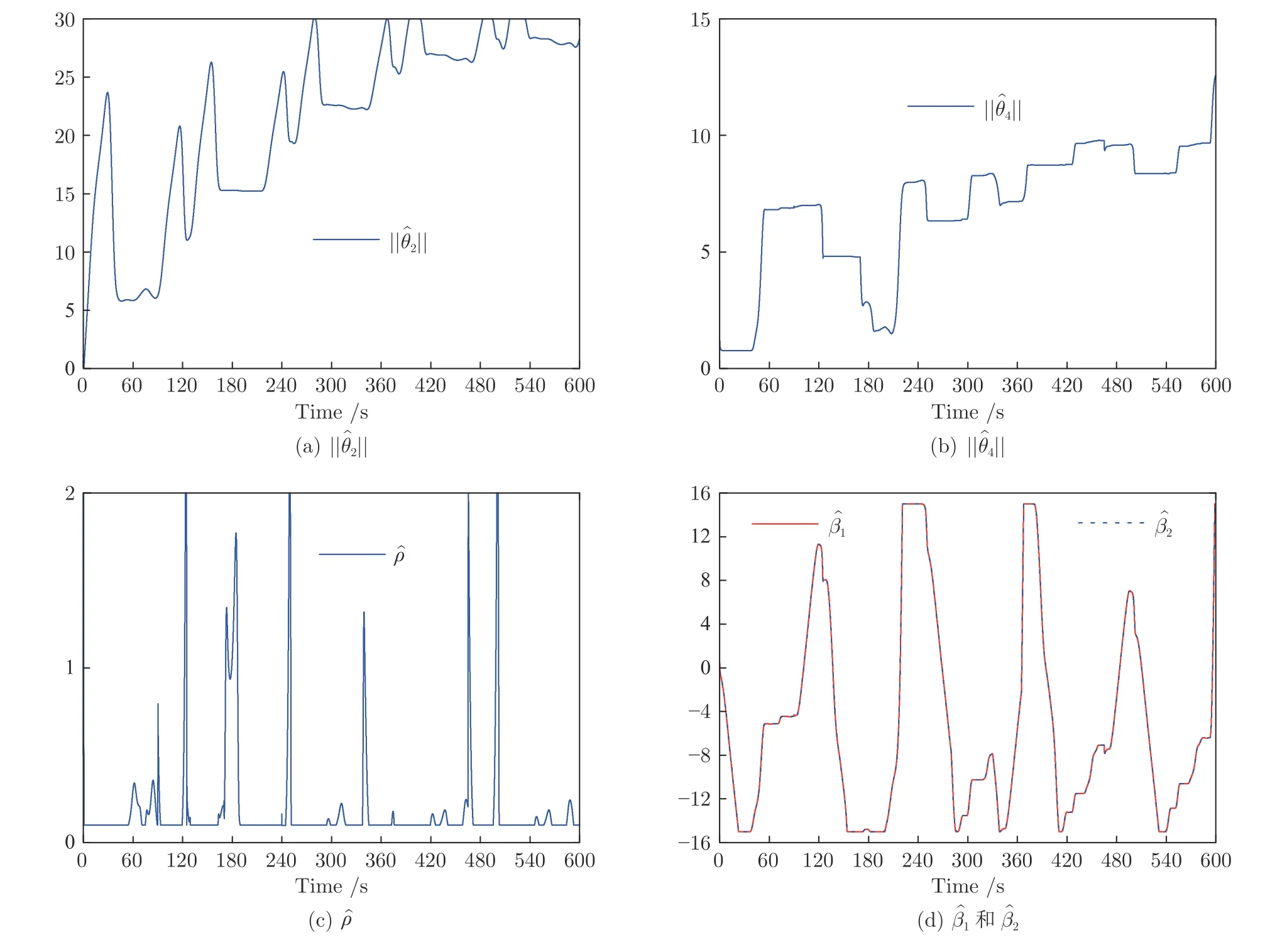
圖17 實驗4 中自適應參數Fig.17 Adaptive parameters in Experiment 4

4 結束語

本文針對一類不確定嚴格反饋非線性系統,提出了一種自適應 CFB 控制方案解決了間歇性執行器故障的補償問題.基于投影算子的參數更新律可保證控制器中估計參數的有界性.即使存在未知參數間歇性跳變的影響,改進的Lyapunov 函數證明了所提出的方案能夠保證閉環系統中所有信號的有界性.同時建立了系統穩定性與Lyapunov 函數跳變幅度,最小故障時間間隔以及設計參數之間的關系.進一步,建立的跟蹤誤差的暫態和穩態指標顯式界說明了通過調節設計參數,可獲得良好的系統暫態和穩態跟蹤指標.最后,四個仿真實例驗證了所提出的控制方案不僅解決了均勻間隔周期執行器故障的補償問題,而且解決了非均勻間隔周期執行器故障的補償問題.

遲滯或者輸入量化等未知非線性現象也經常存在于控制系統的執行器中.因此,結合高增益觀測器技術[32],針對具有遲滯(或者輸入量化)和間歇性執行器故障的系統(1),設計一種自適應輸出反饋控制方案將是下一步的研究重點.

附錄A 定理2 的證明

證明.調用式 (31),式 (25) 定義的 Lyapunov 函數V的導數還滿足

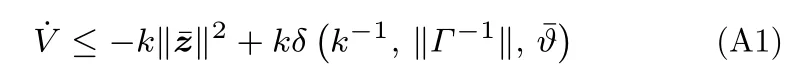
其中,k的定義見式 (27).