基于粒子群優化算法支持向量回歸預測法的大電網電壓穩定在線評估方法

李帥虎，趙翔，蔣昀宸

(1.長沙理工大學電氣與信息工程學院，湖南 長沙 410014；2.國網湖南省電力有限公司長沙供電分公司，湖南 長沙 410011)

0 引言

現代大電網系統中，電網互聯規模不斷增大，不確定性分布式能源大量接入及智能化程度不斷提高，不能大范圍傳輸的無功引起的電壓穩定問題更加突出，這將導致電壓崩潰事故，造成人們生產生活的不便和巨大損失[1-2]。因此，在線電壓穩定評估技術尤其重要。現有電壓穩定的評估大多是基于連續潮流(continuation power flow，CPF)的離線方法進行評估[3-4]，算法具有很強的魯棒性，但因為大多數P-V曲線上的點都要進行潮流計算，導致該方法計算量大，運行較為緩慢，難以滿足在線應用的實時性要求，而且計算時系統增負荷的實際方向難確定，因而具有一定的局限性[5]。

為了滿足傳統方法的在線應用要求，20世紀末科研人員開始將機器學習方法應用到電力系統靜態電壓的穩定評估[6-7]。最早的機器學習方法應用到靜態電壓穩定評估的核心思想是將靜態電壓穩定問題視為一個預測或是分類問題，因此通過傳統方法獲取大量學習樣本供給機器學習模型迭代訓練后，模型可以學習到樣本中系統變量與靜態電壓穩定狀態之間的非線性映射關系。這就實現了系統靜態電壓穩定狀態的快速、高效、可靠評估。但是該技術本質上屬于黑箱模型，對于電壓穩定評估的過程解釋性知識太少，完整清晰的評估過程和機理難以呈現。

為了解決上述問題，一些學者嘗試通過基于同步相量測量裝置(phasor measurement unit，PMU)的廣域監測系統(wide area measurement system，WAMS)監測電壓穩定性，利用PMU數據，可以實現實時異常檢測[8]。在文獻[9]中，PMU數據和深度神經網絡(deep neural networks，DNN)用于在線靜態安全評估。DNN在電力系統安全評估中具有實時計算速度和較強的泛化能力[10]。文獻[11]提出一種基于DNN的靜態穩定極限負荷裕度評估方法。該方法不僅節省了計算成本，還能夠具體區域、具體分析，彌補了傳統連續潮流的缺陷。不過DNN的泛化能力和預測精度還可以進一步提升。文獻[12]提到支持向量回歸模型(support vector regression，SVR)具有學習能力強、泛化錯誤率低的優點，且在小樣本的情況下也可以很好地學習到樣本中的特征。但是該模型對于參數的調節和函數的選擇非常敏感，于是有文獻利用網格搜索法對SVR參數進行優化[13]。網格搜索法被稱為參數調整中的窮舉法[14-15]，但由于搜索空間離散化，一些信息容易丟失，所以利用遺傳優化算法、人工蜂群優化算法和人工蟻群算法等智能算法對參數尋優，極大提高了模型的預測精度[16]。支持向量回歸法的預測精度主要取決于懲罰因子和核函數參數，粒子群算法是一種廣泛應用于各個領域的智能優化進化算法，具有搜索覆蓋范圍廣、收斂速度特別快、精度非常高等特點[17]，而且算法具有本身需要設置的參數少、比較容易實現的特點，被廣泛應用。因此選用PSO算法進行SVR參數的優化選擇，提高了預測精度，取得理想的預測結果。

在此基礎上，本文提出基于PSO-SVR的大電網電壓穩定在線評估方法。該方法利用了SVR模型具有學習能力強、泛化錯誤率低的優點，在小樣本的情況下也可以很好地學習到樣本中的特征，同時克服SVR模型對于參數調節和函數選擇非常敏感的問題。利用PSO算法對SVR模型的超參數進行優化選擇，可以讓SVR模型更好地學習到電網運行數據和阻抗模裕度值之間的非線性關系，采用PSO-SVR模型對阻抗模裕度進行預測。該方法可以大大減少訓練樣本量，并提高預測精度，滿足在線應用的要求。

1 阻抗模裕度的基本原理

電力系統實際上是一個復雜的非線性時變系統。文獻[4]通過戴維南等值原理建立非線性動態等值方法，在此基礎上提出了阻抗模裕度這一局部電壓穩定指標[16]。通過該指標對電力系統進行分析，當電力系統達到最大傳輸功率時，負荷靜態等值阻抗與系統的戴維南等值阻抗之間存在如下關系:

式中，為第i個節點負荷靜態等值阻抗；為第i個節點戴維南等值阻抗。計算公式為:

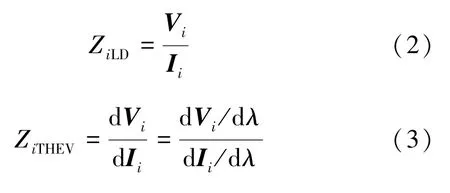
式中，Vi和Ii分別表示第i個節點的電壓和電流。由于電力系統的非解析性，復數域中母線電壓不能對負載電流直接求導，因而設置一個中間變量來進行計算。負荷節點阻抗模裕度(ηi)定義如下:

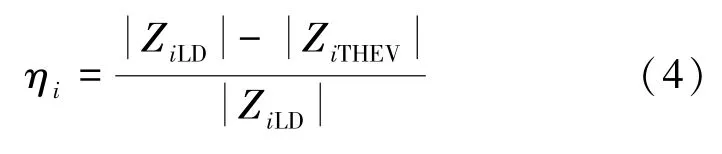
由式(2)和式(3)可知，基于相量測量單元(PMU)測得的節點電壓、電流數據，可計算出負荷節點阻抗模裕度(ηi)。ηi的取值范圍為0～1，當ηi越接近0時，該節點越接近極限狀態。而最小阻抗模裕度決定了系統電壓穩定整體水平。

阻抗模裕度指標可以通過PMU實時采集的節點信息快速計算得到，分析速度基本滿足在線需求，但該方法有一定的局限性。由式(3)、(4)可知，當系統狀態沒有變化或變化非常小時，由于節點電壓差為0，系統等效阻抗等于或非常接近于0，這將導致該節點電壓穩定情況判別有誤。而且，當系統接近極限狀態時，電力系統的非線性較強，容易發生參數漂移現象。為了解決上述問題，本文提出一種基于PSO-SVR的電壓穩定性在線監測方法，可以將其應用于阻抗模裕度預測。

2 建立PSO-SVR模型

支持向量回歸(SVR)是在支持向量機(SVM)的基礎上，引入ε不敏感損失函數而形成的，以適用于回歸用途的一種機器學習方法。兩者間的區別在于:SVM致力于找到一個超平面，盡量使所有樣本能遠離這個超平面，以實現該算法的分類功能；而SVR則致力于在樣本空間中找到一條曲線能夠使所有數據點都盡量離該曲線足夠近，以實現該算法的數據擬合回歸功能。

SVR算法與傳統的神經網絡擬合算法不同，允許擬合過程中存在一定量的偏差ε。因此SVR擬合的f(x)周邊會形成一個以f(x)+ε為上限、f(x)-ε為下限的間隔帶。當數據點落入該間隔帶中時，算法認定該預測結果正確，將不會計算其損失；而一旦數據點不在該間隔帶中，則會被認定該預測結果錯誤，并計算損失值，模型如圖1所示。

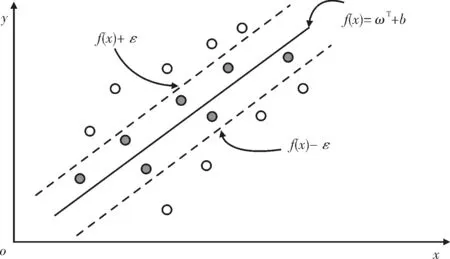
圖1 支持向量回歸模型

從圖1中可知，SVR的最終目的是求解數學模型f(x)中的參數ω和b，其表達式如(5)所示:

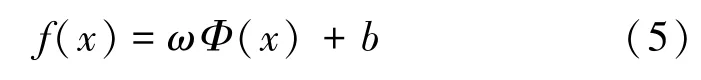
式中，曲線f(x)是線性回歸函數表達式；Φ(x)代表隨映射函數及其權重，x為輸入自變量；b代表偏差。

且在求解過程中，要求滿足一定的約束條件，即:

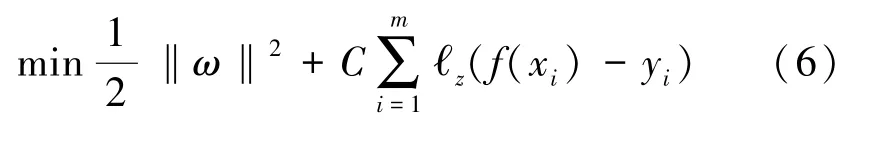
式中，‖ω‖2是為了保證幾何最大間距超平面項；C為懲罰系數，表示能容忍預測值與實際值之間的偏差大小；?z為ε的不敏感系數。?z主要用來控制間隔帶的大小，即當預測值與實際值的偏差在ε范圍內時，則可以不計算損失函數；當預測值與實際值的偏差不在ε范圍內時，則需要計算損失值。其具體數學表達式如下:

在數據采集過程中的不可控因素，導致數據樣本中可能存在少量異常數據點，而這些異常點一旦在模型盡量擬合數據的過程中被較好地學習到了，就會導致整個模型出現過擬合。為了忽視掉這些異常點，并提高整個模型的泛化能力，使SVR算法對樣本數據集的泛化性能和擬合能力較強，需要調參。但是該算法調參比較復雜，且參數變化對預測精度的影響較大。故使用優化算法中表現較好的粒子群算法(PSO)對SVR進行調參優化。

3 PSO-SVR優化策略框架

3.1 訓練數據準備

為使SVR得到充分地訓練，能夠預測出電網薄弱節點在各個負荷水平下的阻抗模裕度，需要隨機生成大量不同負荷水平的電網潮流案例，然后將潮流數據輸入到阻抗模裕度算法中進行計算，由此得到SVR的輸入特征和輸出特征。

為保證所有案例都有可行解，需要使用連續潮流程序對電網的極限負荷水平進行估計，負荷擾動方式為全網負荷同比例增長。使用負荷比例系數k對全網負荷水平進行控制，將k值限定在0到kmax之間，并隨機取1 000個隨機的k值，能夠得到1 000個隨機的不同負荷水平的潮流案例。然后將這1 000個隨機的潮流案例代入阻抗模裕度算法中進行計算，得到各節點的阻抗模裕度。最后將各節點潮流計算后的有功、無功、電壓值以及電壓相角作為輸入特征，將對應的阻抗模裕度的值作為輸出特征，以此來訓練SVR網絡。

3.2 粒子群優化支持向量回歸算法訓練計劃

在進行SVR模型構建之前，采用上述訓練數據的準備方法，對節點有功、無功、電壓值以及電壓相角等相關數據進行了采集，對應的采集數目為1 000條。按照9∶1的比例將訓練集與測試集分開，其中訓練集數據是使用算法隨機抽取900條，剩下的100條數據將作為測試模型，需要進行結果評估。

準備好訓練及測試數據后，在Python中對SVR模型進行構建。在Scikit-learn機器學習庫中調用支持向量機的分支算法SVR，在進行SVR的參數構建時，先對其中三個重要參數采用隨機初始化方法:將懲罰參數C設置為1，不敏感間隔系數epsilon設置為0.1，核系數gamma設置為10。SVR模型的其他參數均使用默認值。

初始模型構建完成后，使用PSO算法對模型的這三個重要參數進行迭代優化。其中PSO的參數設置參考文獻[17]確定方法，見表1。

表1 PSO參數設置表

使用PSO對SVR的三個重要參數(C、epsilon、gamma)進行迭代優化后，將優化后的參數值傳入SVR算法。PSO-SVR算法的流程如圖2所示。

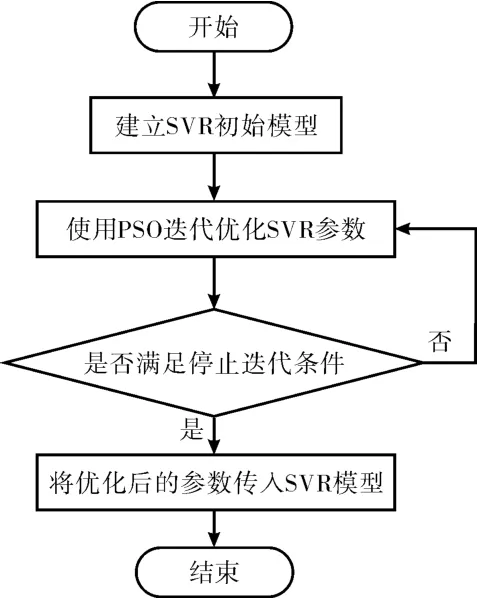
圖2 PSO優化SVR算法流程

3.3 模型表現評估方法

使用以下幾種性能指標[13-14]來評估算法模型的性能:均方根誤差(RMSE)如式(8)所示，主要用來評估測試集整體的誤差水平；最大誤差如式(9)所示，用來評估測試集中單個最大誤差水平。

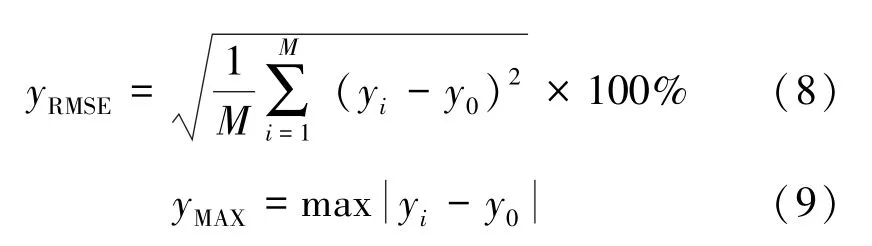
式中，y0為阻抗模裕度算法程序中得到的阻抗模裕度值；yi為PSO-SVR預測的阻抗模裕度值；M是模型訓練所用的數據集個數。

R的定義如下:

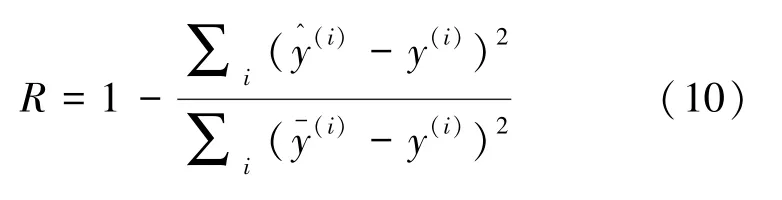
由式(10)可知，損失函數有三種取值極限，分別表示三種不同的模型評估結果。當R=1時，達到最大值，意味著樣本中的預測值和真實值完全相等，沒有任何誤差；當R=0時，分子等于分母，此時樣本的每項預測值都等于均值，相當于模型基本沒有擬合，只是一個均值模型；當R＜0時，分子大于分母，此時訓練模型產生的誤差比使用均值產生的誤差還要大。這種情況通常是模型應為非線性關系，但誤使用了線性擬合方法所致。

由此可知，R指標可以很好地評估模型的整體線性擬合程度。在后續的PSO優化算法中，以R方值作為優化目標進行優化迭代，最終所得的優化參數將是R最大的模型參數。

結合PSO與SVR的方法原理，實現電壓穩定在線評估，基本步驟為:

1)首先設置優化模型的相關參數，進行適應度計算，適應度函數為均方誤差。

2)更新個體最優值，迭代之后計算得到的目前適應度值與之前的歷史最佳值相比較，若當前適應度值更滿足評價標準則取而代之，若不符合則不做改變。

3)更新全局最優值，每次迭代之后比較所有粒子的個體最佳值，把最符合評價標準的那個值取出與目前全局最佳值作比較，若更加符合則取而代之，否則不做改變。

4)更新速度與位置，對當前組合的位置和速度進行調整。然后判斷是否滿足終止條件，當滿足條件時，則迭代終止，否則返回第一步。

5)最后將參數C和g的最優值構建電壓穩定裕度預測優化模型進行預測。

4 仿真計算與分析

4.1 IEEE 118節點系統

為了證明該方法在大規模電網中具有良好的性能，在IEEE 118節點系統上對該方法進行了測試。IEEE 118節點系統是一個大電網。電網接線如圖3所示，其中藍色虛線為聯絡線，粗體紅色虛線為電網分隔線。斷開聯絡線后，該系統分為三個區域電網，相關參數參見文獻[18]。

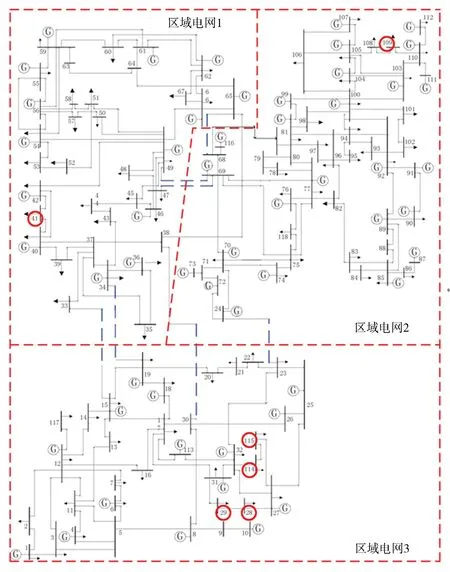
圖3 IEEE 118節點系統接線圖

對于規模大、結構復雜的電力系統，通常采用分區法進行分析。一般情況下，電壓穩定問題從局部地區開始，并逐漸擴展到其他地區，因此確定電力系統的薄弱環節非常重要。根據文獻[14]中的分區原則對IEEE 118母線系統進行分區，其中每個分區代表一個區域電網。IEEE 118節點系統中的五個較弱節點分別為29節點、41節點、28節點、115節點和114節點，這些節點分布在區域電網1和區域電網3中。

4.2 PSO的參數優化效果

首先以IEEE 118母線系統中109號節點為例來說明PSO算法對SVR的參數優化能力。這里使用采集并處理過的數據，并根據SVR模型隨機初始化方法，建立初始回歸模型。在初始回歸模型的基礎上，對數據集進行了首次模型訓練及測試。初始SVR模型的擬合效果如圖4所示。

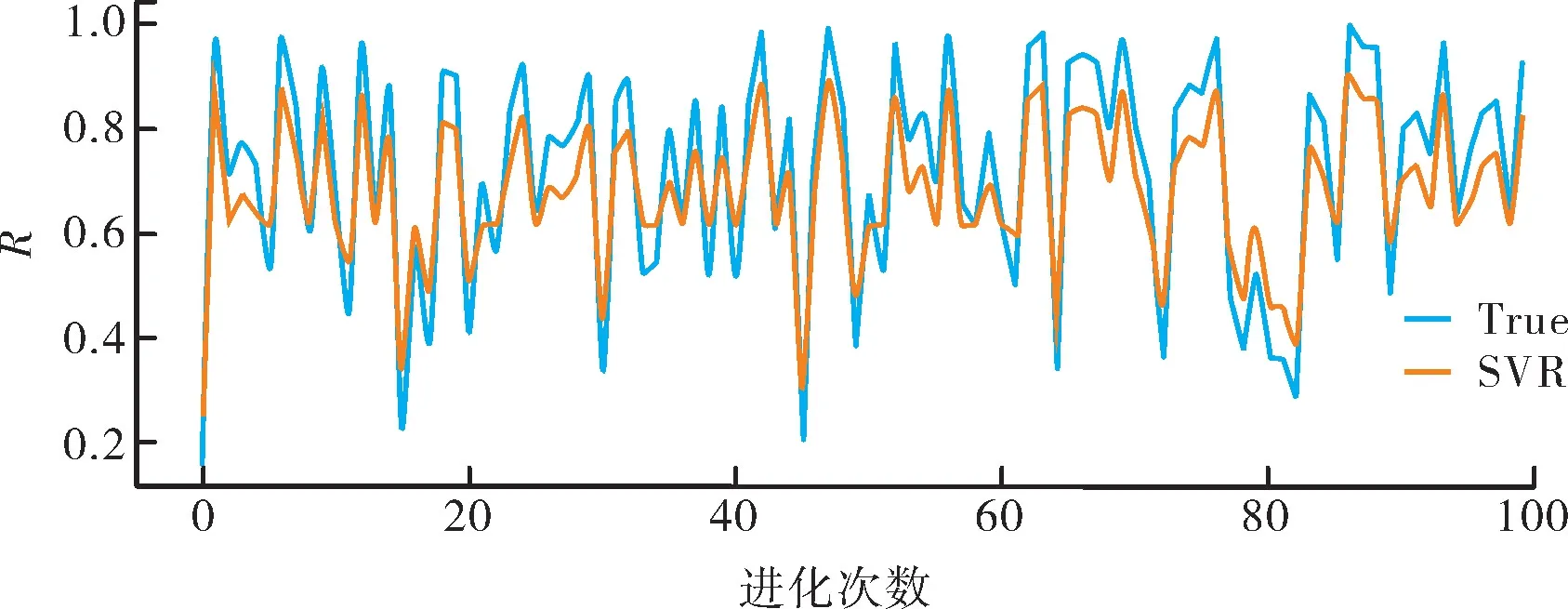
圖4 初始SVR擬合效果圖

在初始模型的基礎上，利用PSO優化方法對初始SVR的三個重要參數(C、epsilon、gamma)進行迭代優化。PSO的參數根據表1設置。經過20輪迭代優化后，優化的參數與原參數的對比見表2。

表2 參數對比表

PSO迭代過程中，R變化曲線如圖5所示。將優化后的參數傳入SVR模型后，重新對數據集進行訓練，擬合曲線和對角線偏差如圖6和圖7所示。

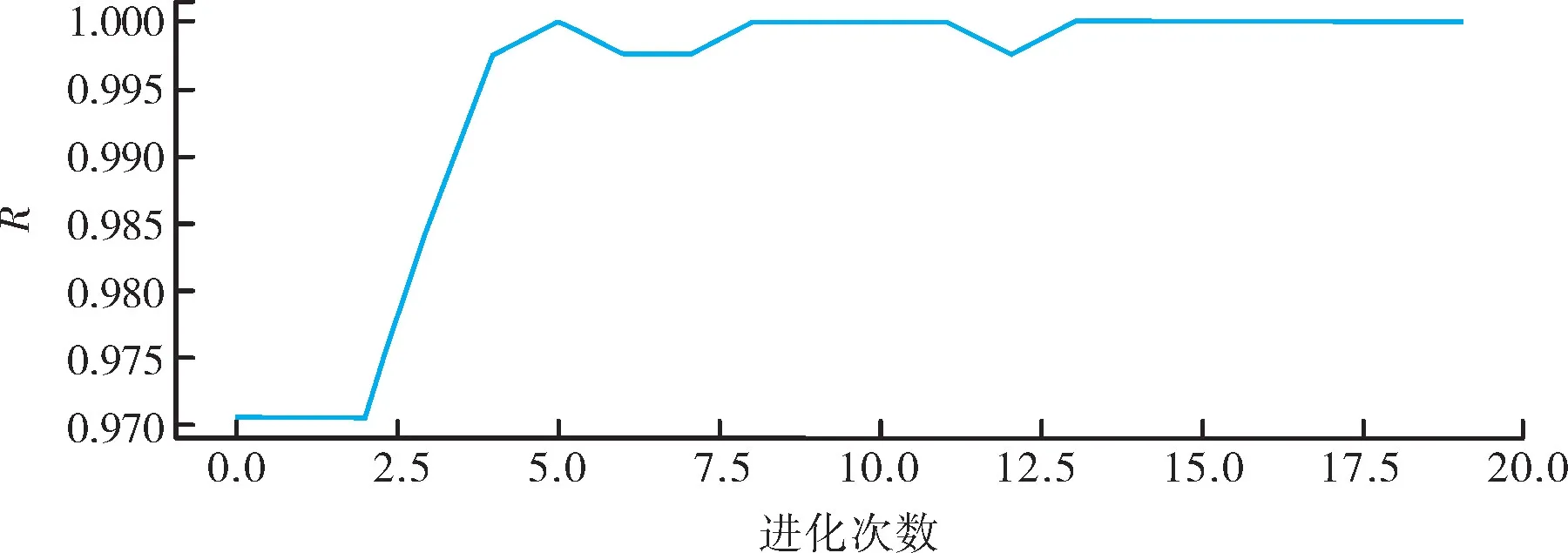
圖5 R迭代曲線

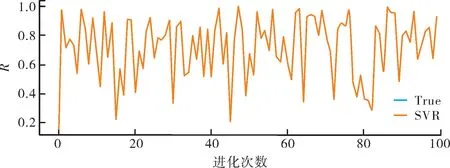
圖6 擬合曲線

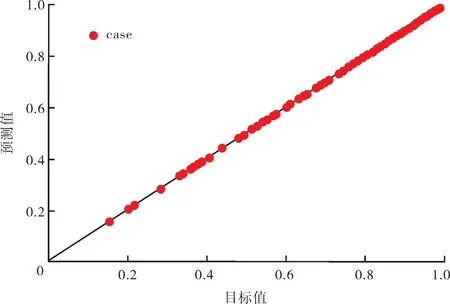
圖7 對角線偏差圖

由圖6和圖7可知，經過參數優化的SVR模型，對測試集的擬合效果有了極大地提升，整體的誤差值極小。優化后SVR與初始SVR的損失函數值的對比表見表3。

表3 損失函數對比表

基于109號節點數據的仿真情況，PSO的參數優化效果明顯，參數優化后SVR算法的擬合效果有顯著提升。

4.3 評估模型表現測試

為對比基于PSO-SVR的方法與基于DNN的評估方法(簡稱DNN)的優劣性，數據集采用的6個數據樣本，分別是29節點、41節點、28節點、115節點、114節點和109號節點的數據。PSO-SVR算法模型通過數據集的訓練后，6個測試集的預測表現評估結果如圖8和表4所示。

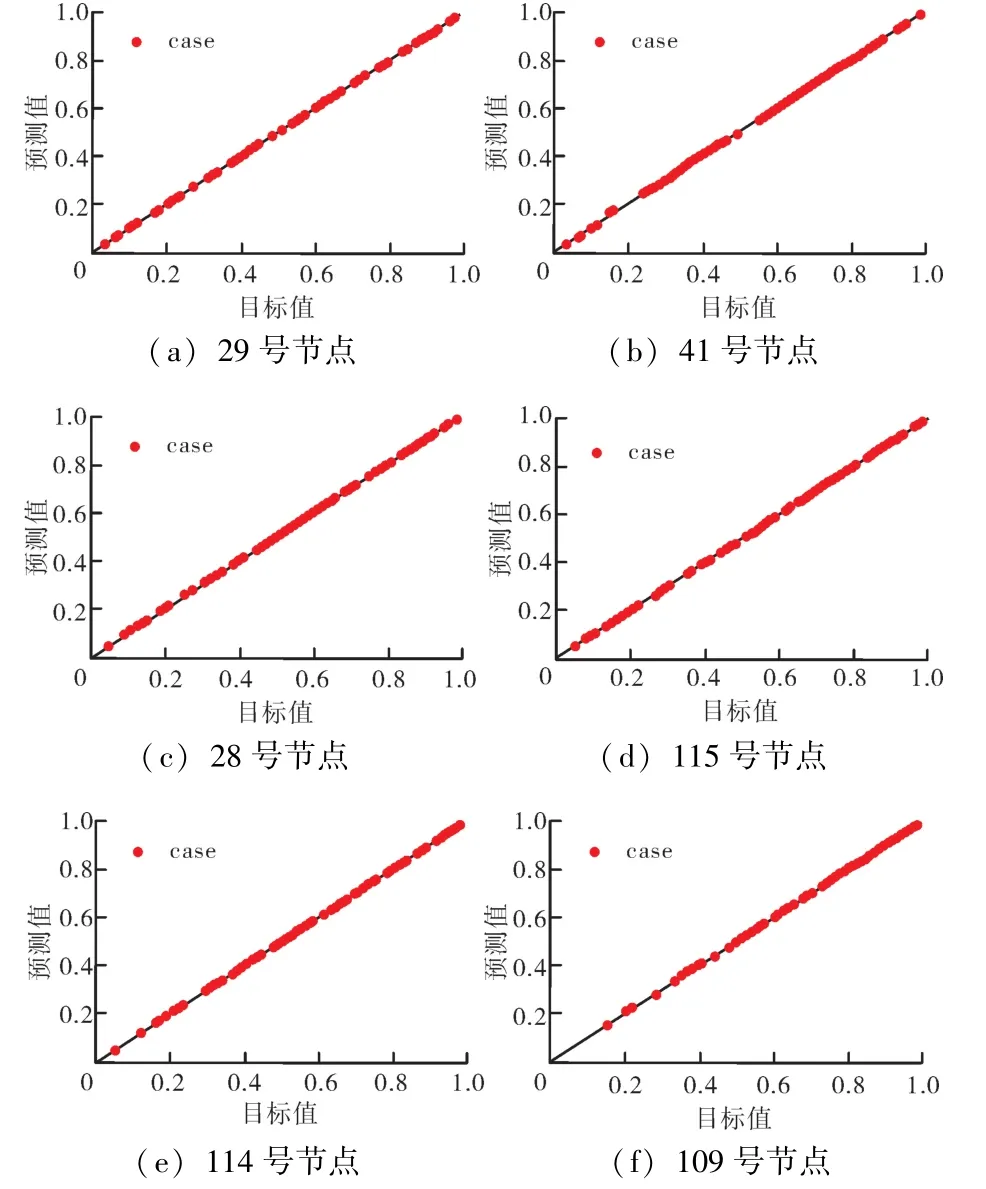
圖8 PSO-SVR模型對不同節點的阻抗模裕度值預測性能

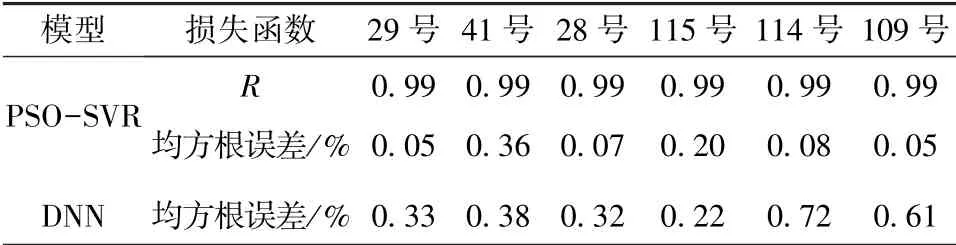
表4 PSO-SVR與DNN的損失函數值對比表

根據圖8以及表4結果，可以發現PSO-SVR方法在預測精度方面對比DNN方案有了一定程度的提高。但是僅對比預測精度不能全面地比較方案的優劣性，計算時間同樣是算法性能的重要組成部分。將PSO-SVR方案與DNN方案的計算時間進行詳細對比，結果見表5。

表5 PSO-SVR與DNN的計算時間對比表 s

可以從表5中看出，PSO-SVR模型在進行參數優化迭代時所花的時間最長，達到了263.415 s的時長，但其所需的訓練時間和預測時間相較于DNN更短，分別只需要1.255 s和0.001 s。同時PSO-SVR模型的參數優化迭代部分可以離線計算，不需要進行線上的實時計算。因此PSO-SVR模型同樣適用于在線使用。DNN模型的訓練同樣也可以離線計算，但其對于100個樣本的預測時間稍長于SVR。因此當數據量較小時，PSO-SVR模型相較于DNN在計算時間方面仍具有一定優勢。

5 結語

本文提出了一種基于PSO-SVR的大規模電網電壓穩定性在線監測方法。該方法基于阻抗模裕度這一局部電壓穩定指標，可以快速辨識電網中的薄弱節點，但在線使用可能會出現電壓穩定情況誤判和參數漂移等問題。而機器學習的發展很好地解決了這些問題。通過109節點證明了優化后的SVR模型可以更好地學習到電網運行數據和阻抗模裕度值之間的非線性關系。然后通過IEEE 118總線系統驗證了PSO-SVR在電壓穩定評估中的有效性，并與DNN進行對比，結果表明本文所提方法速度更快、精度更高。故PSO-SVR模型能夠幫助電網工作人員快速準確判斷系統運行狀態，實現薄弱節點電壓穩定情況的在線監測。