基于ACO-BP的省級月售電量預測

楊宇萌

（河海大學能源與電氣學院，江蘇南京 211100）

0 引言

電量因不能大量儲存，生產和消耗幾乎同時進行的特殊性，其消耗量常被視為表征社會經濟生產穩定的指標。同時，為貫徹落實可持續發展戰略，順利開展售電規劃和發電計劃的合理設計等社會經濟工作，提高售電量預測的準確度成為電網企業長期面臨的重要課題之一。

國內外對售電量的預測常采用與負荷預測相似的方法，因為兩者的波動特性相似。對于中長期的售電量預測，通常會建立灰色預測模型[1-3]、ARIMA[4-6]預測模型。灰色預測模型可以在數據量較小的情況下對呈指數增長的序列進行較好的預測，ARIMA序列通過分析序列的非線性波動建立合適的預測模型，但對波動性較大、非線性較強的序列預測效果不佳。隨著機器學習的興起，越來越多的學者通過機器學習方法進行建模預測，BP網絡因其優越的性能，廣泛應用于預測領域。宋建等人[7]將BP網絡用于GM（1，1）預測優化上，通過對GM（1，1）的預測誤差進行修正，充分發揮BP和GM（1，1）的優勢，提升預測精度。徐揚等人[8]用遺傳模擬退火算法對BP網絡的權重進行修正，提升BP網絡的預測效果，改善網絡陷入局部最小值的問題。陳先飛等人[9]通過構建多變量灰色遺傳的中長期預測模型，顯著提升了預測準確度。徐源等人[10]基于數據的聚類法進行預測，避免了復雜的調參過程，提升了預測的效率。吳耀武等人[11]采用Dempster合成法與Yager組合規則，提出了基于改進證據理論的預測模型。

為了改進BP網絡初始權重和閾值難以確定導致的模型預測精度較低的問題，可以采用蟻群算法（ACO）進行尋優，但蟻群算法同樣可能由于信息素更新問題陷入局部最優或訓練時間過長。因此，本文將對ACO進行信息素更新的改進，并利用改進的ACO算法對BP網絡的權重和閾值進行尋優，以提升BP網絡的預測精度和速度。

1 預測模型

機器學習算法對訓練樣本的依賴度高，數據樣本中所包含的信息量的多少將直接影響算法的訓練效果。月售電量是非線性、非平穩的時間序列，在對月度售電量進行預測時，春節效應對神經網絡訓練效果的影響不可忽視。春節假期售電量較少，若預測春節假期在2月的某年各月的售電量，訓練過程中采用的數據既有春節假期在1月的又有春節假期在2月的，月售電量預測結果將會偏大。

為了解決這一問題，本文利用EMD（Empirical Mode Decomposition）分解法將月度售電量的殘余分量分離出來，并剔除春節假期與預測年春節假期不在同月的數據，然后提取本征模態分量，對各個分量建立預測模型，將各個分量的預測結果相疊加得到月售電量。

1.1 EMD分解

EMD分解，是一種能將時間序列x（t）分解為若干個本征模態函數（imfk）和一個殘余分量（rk）的函數。每個本征模態函數都將同時滿足以下兩個基本條件：

（1）整個時間范圍內的函數極值點個數和過零點個數要求一致，最多不得大于一個；

（2）任意時間點上的局部最大、最小的包絡線均值必須是零。

給定一個信號x（t），對其進行EMD分解，具體步驟如下：

（1）找出x（t）所有的極值點。

（2）通常采用三次樣條函數擬合出所有極小值點形成下包絡emin（t）和所有極大值點形成上包絡emax（t）。

（3）計算兩條包絡線的均值m（t）：

（4）對原信號進行分離得到新的信息序列xk（t），若能夠滿足判斷條件，則稱xk（t）為該信號的本征模態分量imfk。

其中：

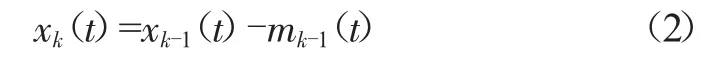
（5）分離出模態分量后，將原始信號x（t）減去本征模態分量imfk后得到殘余分量，記為ri（t）。

（6）對殘余分量重復步驟（1）～（5），直到殘余分量為常數或者單調信號。

綜上可知，原始信號可以表示為：

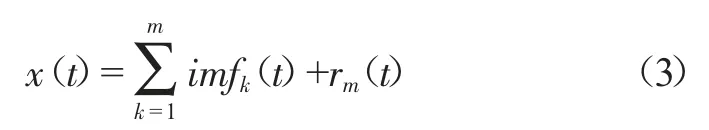
通過對時間序列進行EMD分解，能夠得到時間序列的特征變化量，降低原始序列的波動性和復雜性。

1.2 ACO優化BP算法

1.2.1 BP網絡

BP神經網絡是多層感知器的一種，其加入了誤差逆向傳播環節的反饋機制，廣泛應用于研究領域。BP神經網絡的運作核心是輸入量經過隱藏層的正向傳播得到輸出量后，通過計算輸出量與期望輸出量之間的誤差，將該誤差反向傳播，并在反向傳播的過程中不斷修正連接權重和閾值，不斷減小網絡的誤差，直到誤差趨近于零。

BP算法有下列優點：（1）當BP神經網絡具有足夠多的隱藏層神經元時，可以擬合任意非線性函數；（2）BP神經網絡是一種全局擬合算法，具有較強的泛化能力。

BP網絡基本結構如圖1所示，由i維的輸入層X、中間的j個神經單元的單隱藏層J和m維的輸出層Y構成。

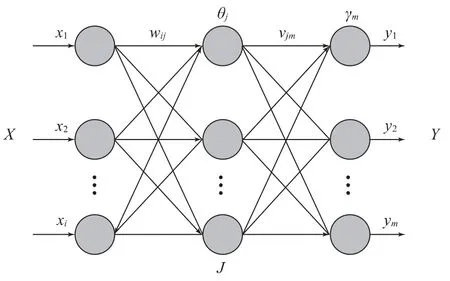
圖1 BP網絡結構

隱藏層的神經元個數常使用如下經驗公式來確定，其中a為[1，10]的常數。

隱藏神經元的輸出為：

輸出層的輸出為：

其中f為激活函數，常用的激活函數為Sigmoid函數。

誤差函數可以表示如下，用于判斷網絡和修正網絡參數。

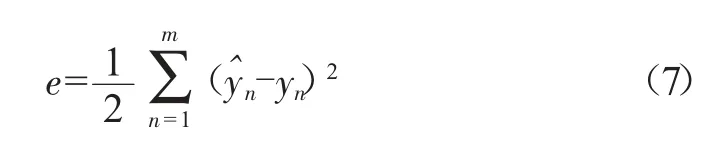
初始權重和閾值的選擇不當將直接影響BP算法的效果，本文采用ACO算法先對初始權重和閾值進行尋優以改善陷入局部最優、收斂速度慢的問題。

1.2.2 ACO-BP網絡

ACO優化BP網絡的基本思路是用螞蟻尋找出BP所有的權重和閾值解空間，因信息素的揮發性，最短的路徑上將留下最高的信息素濃度。一段時間后，選擇最短路徑的螞蟻逐漸增多，最終將集中在最短路徑上，該路徑所確定的解就是最優權重和閾值。流程圖如圖2所示。

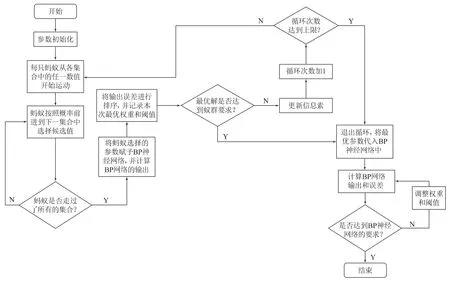
圖2 改進的ACO-BP流程圖

具體步驟如下：

（1）初始化。首先判斷待優化權重和閾值的維度i、權重和閾值的取值區間，將每個區間N等分，在各個子區間內確定一個候選值，該區間內的所有候選值構成一個集合c，共有i個。N的個數不是越多越好，過多將會延長蟻群尋優的過程，而且不能有效改善BP網絡局部最優的問題。設置螞蟻的個數、網絡的預期誤差e*、最大迭代次數tmax、信息素常數Q。

（2）各個螞蟻初始在候選值上，按照一定的概率進行移動，選擇下一個集合的某個候選值，直到所有的螞蟻在i個集合中均完成候選值的選擇。選擇集合c中元素j的概率可以表示為：

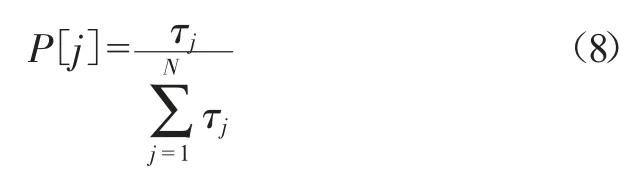
式中：τj為元素j上的信息素含量。

（3）在所有螞蟻都在集合c中根據上述公式選擇到候選值后，即可得到該迭代次數下的權重和閾值組合，將其賦予BP網絡計算BP誤差，將誤差從大到小排列，記錄本次的最優解。

（4）判斷最小誤差與期望誤差e*，若最小誤差小于期望誤差，則轉至步驟（6），否則更新信息素。

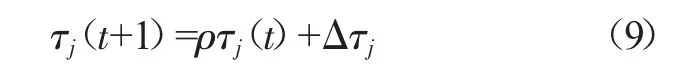
式中：ρ為信息素留存系數，取值區間為[0，1]。

為避免ACO過早陷入局部最優，可對ρ進行改進，將其根據迭代次數的增加自適應改變：

Δτ為上期循環后信息素的變化量，本次迭代中每只選擇j元素的螞蟻均會對j的信息素進行更新，它是由信息素常數Q和上期迭代的網絡誤差ek決定的。為了使蟻群的收斂速度加快，在更短的時間內通過信息素的更新，更快地判斷候選值的優劣，引入信息素增強調節因子λ對信息素進行更新，具體公式表示如下：

（5）迭代次數加1，判斷是否達到最大迭代次數tmax，若達到則轉至步驟（6），否則轉至步驟（2）。

（6）跳出ACO循環，將尋找到的權重和閾值賦予BP網絡，進行BP網絡的迭代。

采用均方根誤差RMSE（Root Mean Square Error）、平均絕對誤差MAE（Mean Absolute Error）和決定系數R2對擬合結果進行評價，用相對誤差對預測結果進行對比。

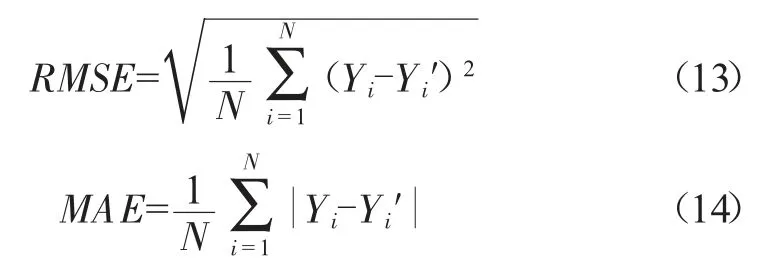
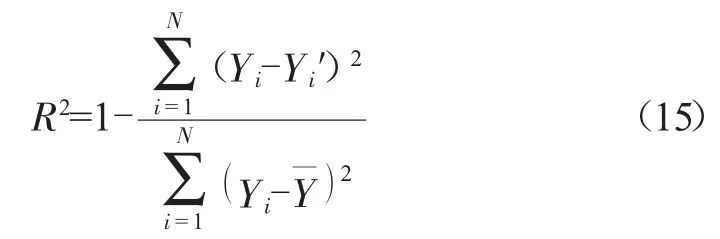
式中：Yi為真實值；Yi′為預測值；為真實值的平均值。

RMSE和MAE的數值越小越好；R2的數值越大越好，取值范圍為[0，1]。

2 實證分析

本文采用來自某省電網公司的歷年的月售電量數據進行實例分析。首先，對月售電量的基本特性進行分析。圖3（a）展示了2010、2013、2016年的月售電量，這三年的春節假期均在2月，且整體趨勢相差不大，2月的售電量最低；圖3（b）中2014年的春節假期位于1月，相較于其他兩年，售電低谷在1月。

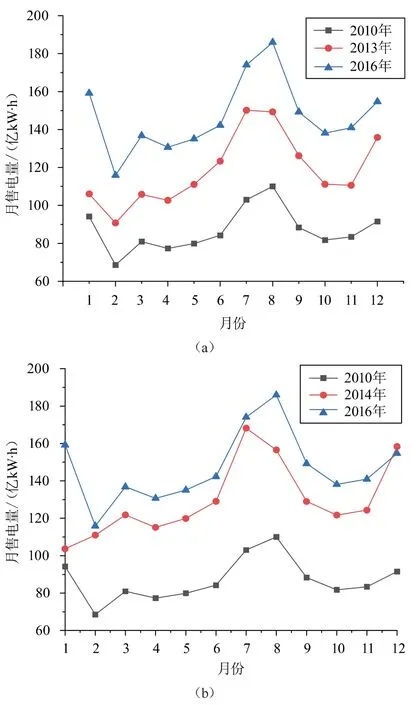
圖3 月售電量特征

利用已獲得的某省2010—2020年月售電量數據，除去春節假期在1月的2012、2014、2017、2020年月售電量數據，將剩下的月售電量數據進行EMD分解，獲取到4個本征模態分量和1個表示整體趨勢的殘余分量，可以發現月售電量的整體趨勢是逐年增長的。EMD分量如圖4所示，其中（a）～（d）為高頻分量，最能表現出月售電量的波動趨勢。

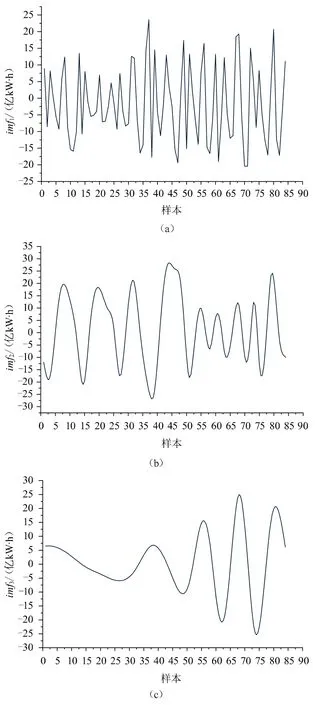
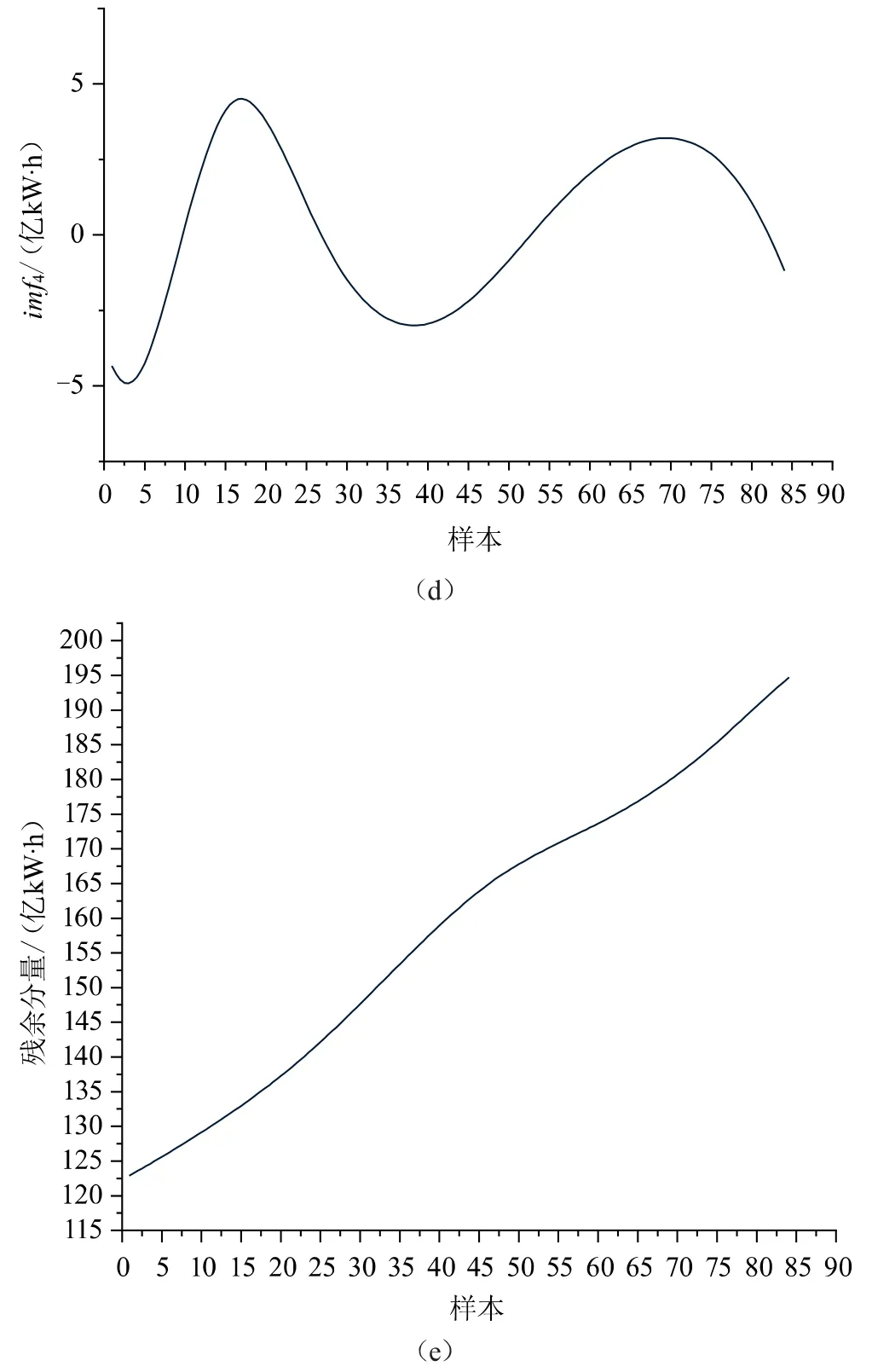
圖4 EMD分量

利用這7年的EMD分解量分別用神經網絡進行81個周期的訓練，然后對2021年的月售電量進行預測。預測流程如圖5所示。

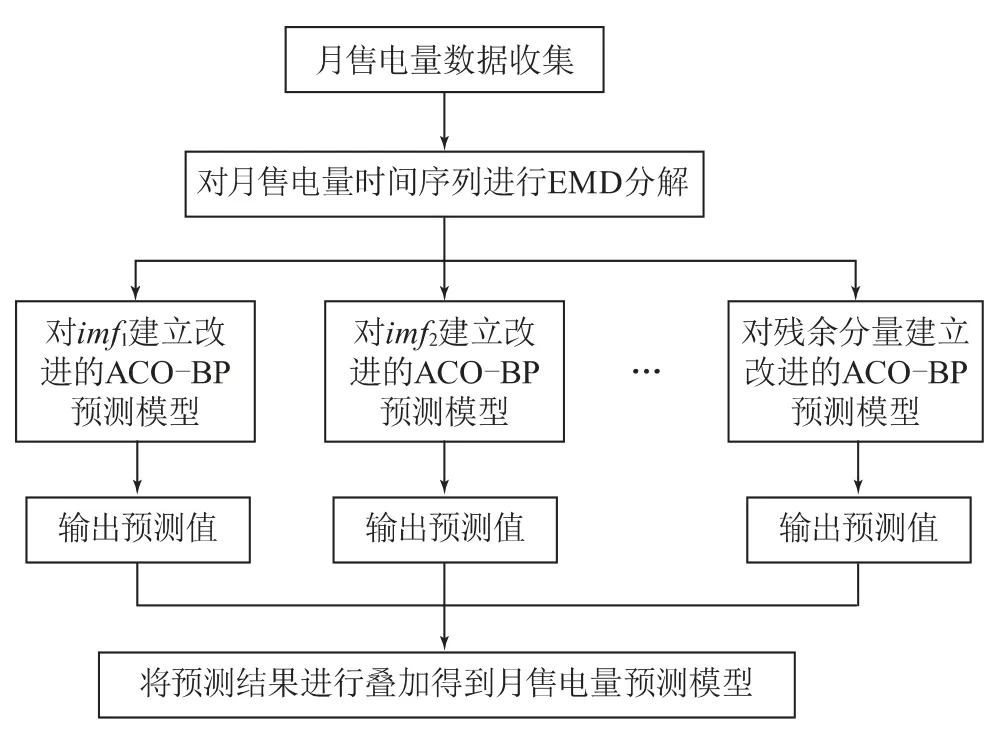
圖5 月售電量預測流程

對于每個EMD分量，其輸入層的節點數為3，即每次預測需要讀取前3個時間點的數據，最大訓練次數為500，學習率為0.001，輸出層的節點數為1，對應預測的EMD分量數值，可判斷出隱藏層的節點個數的取值范圍為[3，13]。對每個節點取值進行10次BP神經網絡試驗，用MSE衡量預測的優劣，選擇對應的MSE最低的隱藏層數。最終選擇各個分量在隱藏層的層數分別為6、13、15、3、4。

對于改進的和未改進的ACO-BP神經網絡，imf1待優化的參數維度為31，取值的區間為[-2，2]，將區間等分為100份，選擇螞蟻的個數為120，信息素的留存系數為0.8，信息素常數Q取20，最大迭代次數為1 000，允許最大誤差e*為0.000 1。BP網絡的輸入層節點數為3，輸出層節點數為1，隱藏層節點數為6，學習率為0.001，最大迭代次數為1 000，允許最大誤差e*為0.000 2。圖6展示了改進的ACO-BP對2021年EMD分量的預測結果。

從圖6可以觀察得出，本征分量的預測準確率相對較低。這是由于本征分量為高頻分量，其變化規律較為復雜，學習較為困難。相反，殘余分量是長期變化的趨勢分量，曲線較為平緩，其預測值與真實值相差較小。將5個分量相疊加即可得到2021年月售電量的預測值，預測值與真實值對比如圖7所示。

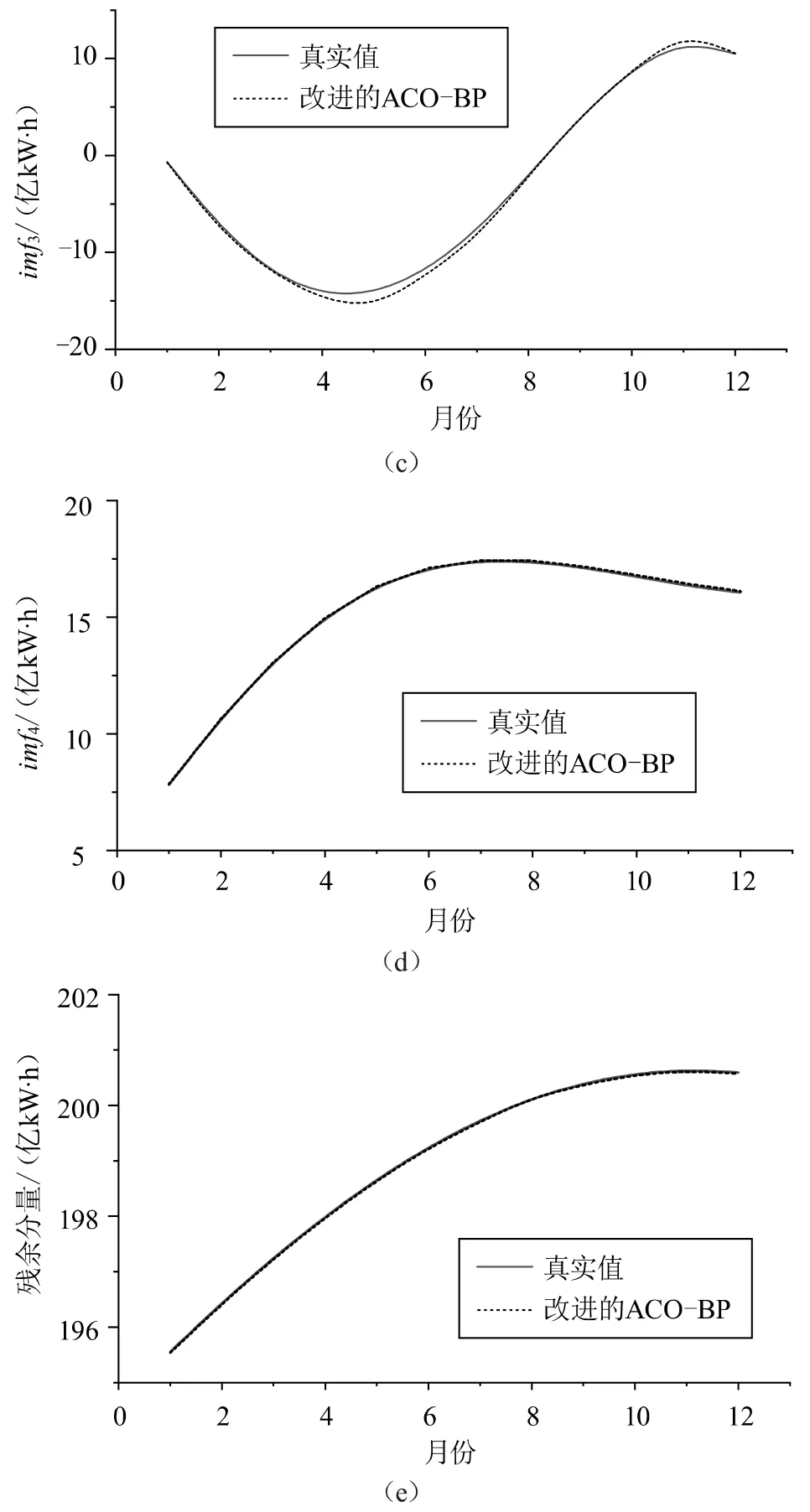
圖6 改進的ACO-BP對EMD分量的預測結果

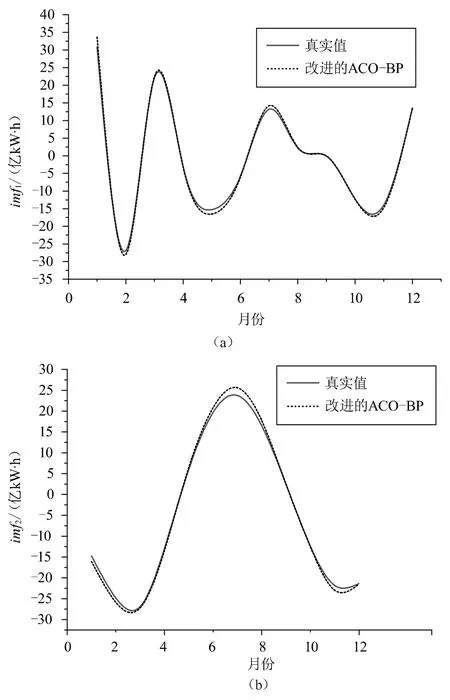
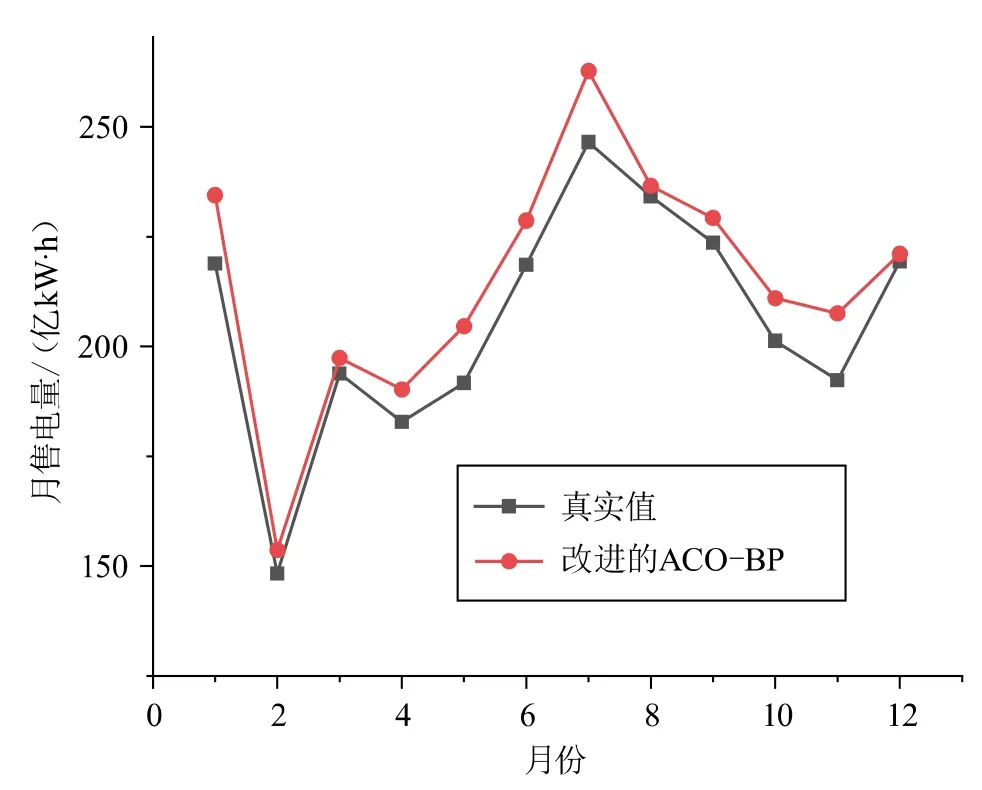
圖7 改進的ACO-BP預測結果

同樣可以使用ACO-BP、BP網絡對EMD分量進行學習，將分量的預測結果疊加即可得到最終的預測結果。將BP、ACO-BP、改進的ACO-BP的預測結果進行對比，如圖8所示，3種預測模型均能很好地預測出月售電量的變化規律。

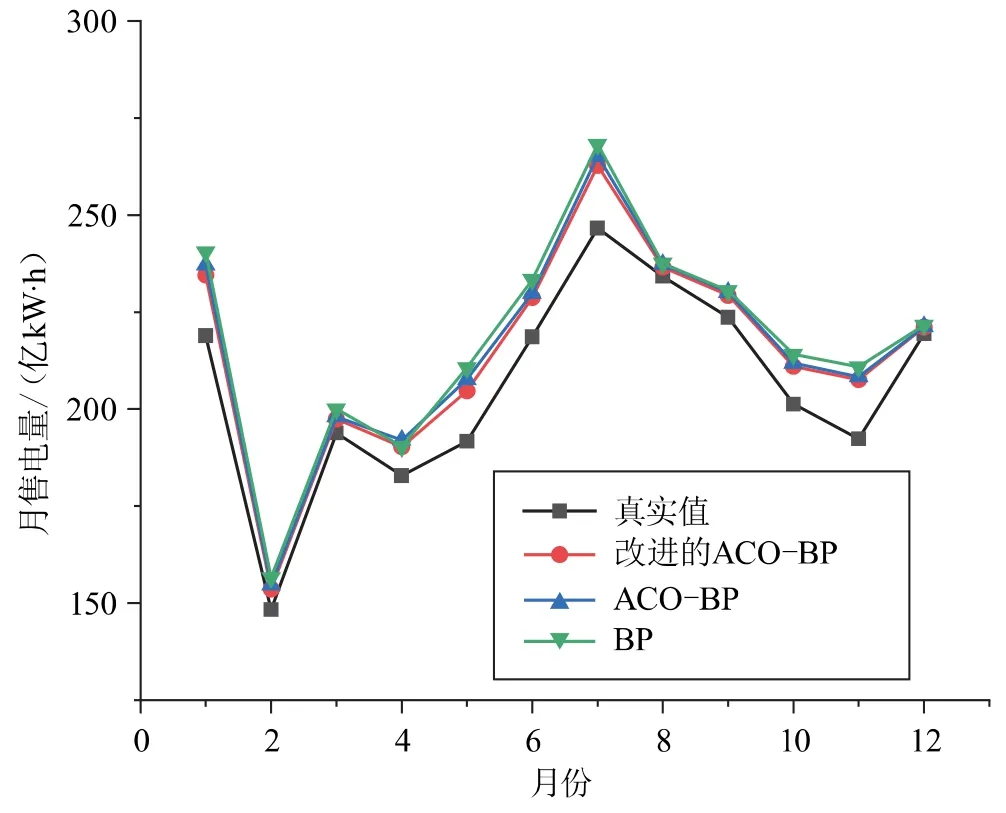
圖8 BP與ACO-BP預測結果對比

從表1的對比可以看出，改進的ACO-BP預測精確度更高，決定系數R2最高為0.982 186，均方根誤差RMSE和平均絕對誤差MAE最小。

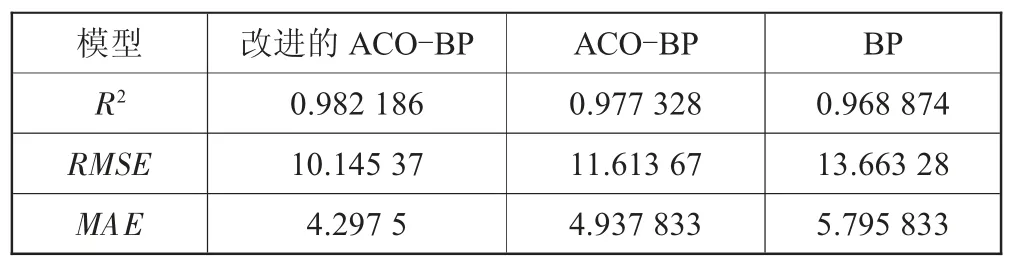
表1 預測結果

表2對比了3種算法達到最大誤差時對應的迭代次數。改進的ACO-BP迭代次數最少，相較于ACO-BP和BP的迭代次數分別減少了32.3%和53.1%。

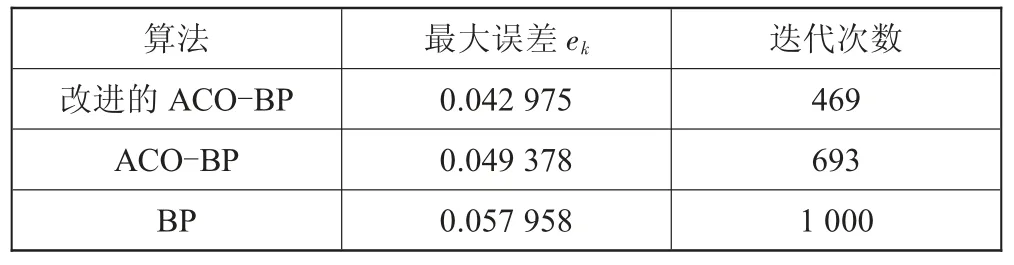
表2 迭代結果

表3進一步展示了3種預測模型的預測結果和相對誤差。通過對比可以發現，改進的ACO-BP最大相對誤差為7.91%，相較于ACO-BP和BP，最大相對誤差分別降低了4.92%和18.03%。

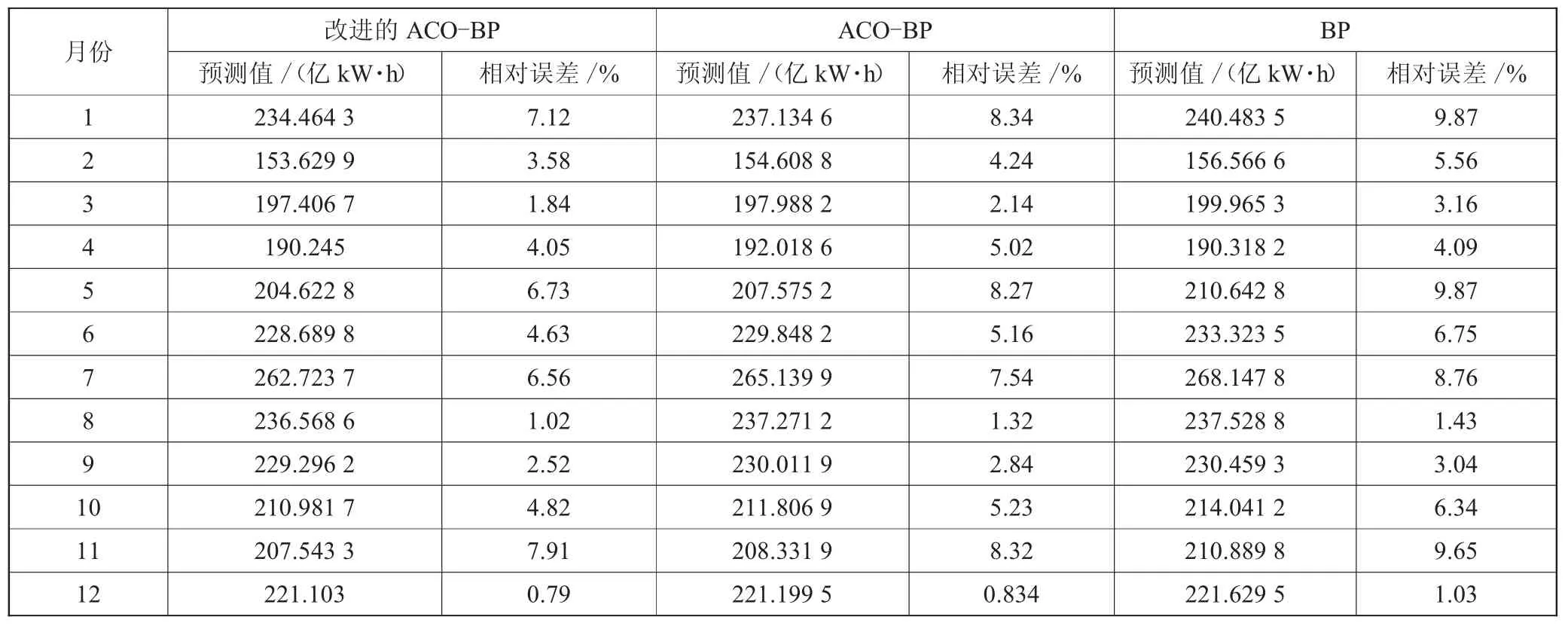
表3 預測結果

3 結語

本文建立了基于ACO-BP的神經網絡預測模型，通過對月售電量時間序列的分析和分解預測，消除由春節假期帶來的預測上的干擾。同時，對傳統的ACO優化模型進行了信息素增減量和留存系數更新的改進，該方法可以更大程度上發揮ACO全局尋優和BP的泛化能力。對某省的月售電量進行預測試驗，結果表明，改進的ACO-BP模型精度更高，能夠有效進行月售電量的預測。