基于神經網絡的室內單站精確被動定位技術研究

張倩倩 尹成友 李安琪

（國防科技大學電子對抗學院,合肥 230037）

引 言

隨著社會科技進步的不斷發展，位置服務在人們生活中已經不可或缺.當前，室外定位的技術已趨于成熟，利用北斗系統、全球定位系統等就能夠基本滿足人們戶外活動的需求.室內定位是近年來的研究熱點，由于室內環境的復雜性以及多徑效應的影響，信號的傳輸會受到一定的影響.復雜的傳輸信道會對信號造成反射、散射以及折射等，很多室外定位方法在室內環境下的定位效果并不理想.

室內定位系統可以分為兩大類：一是傳統的定位方法，不利用復雜多信道信息，依靠測量到達時間、到達時差、往返時間和到達角等參數來估算目標位置；二是利用復雜多信道信息的定位方法，將每個位置用唯一的信道指紋表示，室內定位系統從測量參數中提取特征，通過對多信道傳遞特征的分析，從而實現對目標的定位.

超寬帶(ultra wide-band,UWB)系統具有提供高精度定位的能力，Segura 等人[1]提出了一種新型的UWB 室內定位系統，綜合信號到達時間和測距估計方法，95%的位置測量結果誤差在20 cm 以下，能夠實現在室內環境下對移動機器人的精確定位，但在非視距環境下準確度不夠.文獻[2]針對這種問題，基于樸素貝葉斯原理，對兩種場景進行精確識別，從而提高了非視距環境下的整體定位精度.但現實生活中，由于室內環境的復雜性，如目標的移動、信號衰減和多徑傳播等，UWB 定位技術仍面臨著重大挑戰.

在復雜場景下，傳統定位方法往往受限于室內多徑效應，難以從接收信號中提取目標位置的有效信息，而基于復雜多信道信息的定位方法，通過合理利用這些信息，可以提升定位效果，實現對目標的精確定位.

時間反演[3-4]是一種典型的利用復雜信道信息的定位方法.Hoefer 等人[3]通過數值實驗，利用時間反演腔模型和時空離散傳輸線矩陣方法，重建空間中多個脈沖源，實現了對目標的超分辨定位.文獻[4]通過在目標輻射源近場放置散射介質薄片，當時間反演與散射介質相結合時，能夠提高對目標輻射源的定位精度，以網格分辨率重建脈沖點源的位置和幅度.時間反演方法定位精度較高，但主要用于目標對外輻射信號的情況，是對輻射源自身的定位.

利用接收信號強度(received signal strength,RSS)和信道狀態信息(channel state information,CSI)的指紋定位技術是另一種典型的利用信道信息的定位方法.劉召偉等人[5]依據差分-距離損耗模型，利用RSS 估計距離，由已知距離下的差分接收功率值擬合得到模型參數，用最大似然法估計用戶位置.李若南等人[6]為了降低室內復雜信道對接收信號強度的干擾影響，提出通過注意力機制捕獲RSS 序列與區域位置粗細粒度特征的映射關系，進而獲取區域位置信息，實現了不同大小網格采集下對目標的高精度定位.但RSS 是粗粒度信息，常常受到多徑效應及噪聲信號的影響，因此CSI 指紋定位技術更受青睞.Kaishun Wu 等人[7–9]通過研究正交頻分復用(orthogonal frequency division multiplexing,OFDM)系統中子載波的頻率分集，提出了一種利用CSI 在接收機上建立傳播模型和指紋識別系統的方法[9]，利用OFDM中的信道狀態信息建立傳播模型，將其與頻率分集結合、多天線與空間分集結合用于室內位置指紋識別.在幾個典型室內環境下開展實驗，能夠明顯提高定位精度.在此之后，Wang 等人利用深度學習的方法，分別提出了Phase-Fi[10]和Deep-Fi[11]兩種定位系統.Phase-Fi 系統提取CSI 相位信息，利用網絡權值表示位置指紋，在實際室內環境中實驗，能夠實現客廳1.03 m 和實驗室1.98 m 的平均定位精度. Deep-Fi 系統也能在不同實驗情況下實現米級定位精度.文獻[12]提出一種基于卷積神經網絡(convolutional neural network,CNN)的定位方法，該方法利用不同信道的CSI 振幅和相位差構造位置指紋，與Phase-Fi 系統相比，定位精度提高了57.64%.但基于CSI 定位的前提條件是該區域無線基礎設施較為完善，能夠實現Wi-Fi 信號的全覆蓋，但在部分場景中難以具備這樣的條件，難以實現對目標的精確定位.

在上述的定位方法中，主動定位方法通常需要在空間中布設多個接收傳感器，一般用于目標自身對外輻射信號的情況，難以實現單發單收情況下對目標的定位.而在被動定位情況下，對目標的定位精度通常只能達到米級，無法實現超分辨定位.因此，如何在室內復雜電波傳播環境下，利用單接收站實現對目標的超分辨被動定位，仍然有很多問題亟待解決.

本文基于多徑復雜信道的室內定位理論，將復雜室內環境視為二維的時間反演腔模型，利用不規則的墻壁增強目標與復雜場景中的障礙物的相互作用，進一步增強多徑效應，從而接收的電磁波中也包含了更加豐富的目標信息，最終能夠實現復雜室內環境下對目標的單站精確定位，為室內定位提供了一種新的方法.

1 基于多徑復雜信道的室內定位原理

假設我們考慮圖1 所示的室內定位問題.有一個輻射源位于A(rt)點，有一個接收傳感器位于B(rr)點，有一個目標位于C(r0)點.A點輻射源輻射的信號在室內空間傳播，照射到C點目標，產生散射信號，該信號經過多徑傳輸到達B點接收點.現在的目的是利用B點的單站接收信號對C點目標進行定位.

圖1 室內環境示意圖Fig.1 Schematic diagram of indoor environment

輻射源輻射的信號記為st(t,rt)，經過多徑傳播到達目標點的照射信號為

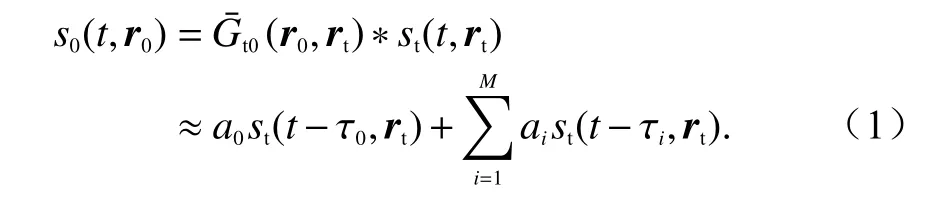
式中：*表示卷積運算；M表示室內復雜環境下有M條信號傳播路徑；ai為第i條信道接收信號的幅度；τi為第i條信道的時延.電磁波在近場傳播過程中，包含物體、墻壁之間的相互作用，是一個非線性過程，所以我們這里用一個信道傳遞函數(r0,rt)來表達，其中包含了目標位置信息.式(1)中第二行將傳輸信道近似為一線性多徑信道，第一項表示在視距情況下接收點接收到的直達波信號，第二項表示經過各種反射、散射的多徑信號的疊加.

式(1)中的照射信號與目標作用后產生散射信號，經過多徑傳輸信道到達接收傳感器后的表達式為

圖2 是在室內二維情況下，利用電磁仿真軟件計算產生的2PSK 發射信號和兩個不同位置目標的接收信號的波形圖.

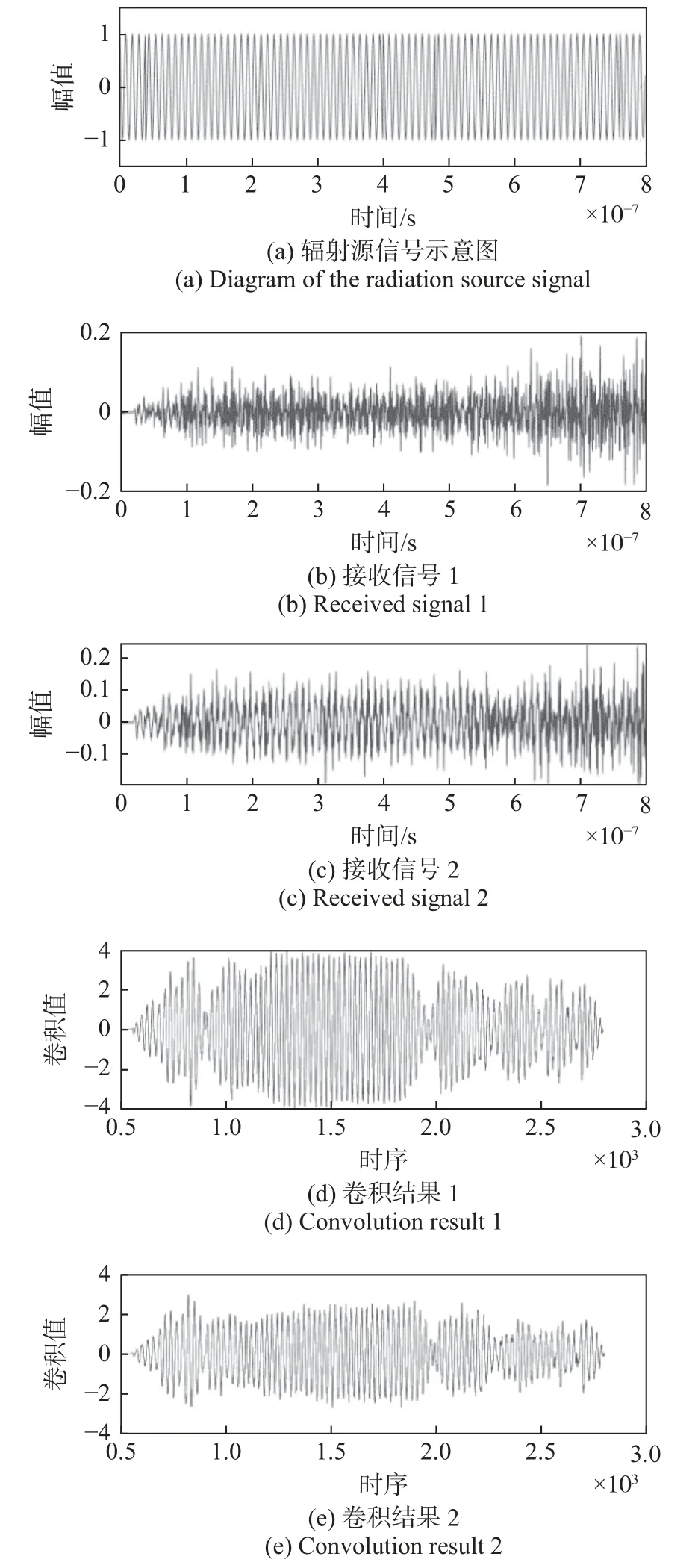
圖2 發射信號和接收信號示意圖Fig.2 Schematic diagram of transmitted and received signals

圖2(a)為發射的2PSK 信號，圖2(b)和(c)為目標位于不同位置點的接收信號.從圖2(b)、(c)可以看出，由于復雜傳播信道的作用，不同位置目標經過兩次復雜信道的傳輸，在接收點的信號包含了豐富的多徑信息.我們利用發射信號與接收信號卷積來近似觀察復雜信道特征，得到圖2(d)和(e)，這些信號的起伏特征可為不同位置目標定位提供重要信息.

從信息角度來考慮，由于復雜室內環境中的多徑效應，接收信號包含更多的目標位置信息.由于不規則墻壁的存在，信號傳播過程中會出現多次反射、散射的現象，在這一過程中，一方面由于復雜傳播信道中格林函數的貢獻，另一方面由于目標與障礙物間的復雜相互作用，包含的倏逝波信息轉移到傳輸波，從而接收點的接收信號中會包含攜帶目標位置精細的細節信息.利用這些信息，就能夠實現對目標的精確定位，甚至超分辨定位.

接收信號中信道傳遞函數(r0;rr,rt)中包含目標位置信息，當室內環境確知，輻射源位置rt和接收傳感器位置rr也確知的情況下，它包含目標位置信息r0，輻射信號是其作用對象.對于常規的Wi-Fi 類信號，其載頻f0已知，調制樣式ms已知.問題是如何利用這些已知信息對r0實現最優估計？

從式(4)可見，r0與接收信號之間是一個復雜的非線性函數關系，要寫出這樣的表達式非常困難，如何求解式(4)，我們自然想到機器學習的方法.

2 基于深度學習的定位算法實現

神經網絡的通用近似定理告訴我們，深度學習神經網絡可以逼近到任何一個連續有界非線性函數.因此，我們可以通過神經網絡學習的方法解決式(4)的問題.

本文根據電磁仿真的訓練數據集，合理設計深度學習CNN 結構，將定位問題轉化為回歸模型的問題.通過數據采集、特征提取和模型訓練，建立信道指紋與位置之間的非線性關系來完成被動定位.

2.1 數據集的產生

考慮圖3 所示的二維典型的三居室房間布局情況下的定位問題.其中，Nx、Ny是每個房間對應剖分的網格數，在本文設定的場景下，Nx、Ny是常數.為了模擬整個空間電磁波的傳播，我們在房間墻壁外設置了一個完全匹配層(uniaxial perfect lymatched layer,UPML).

對場景參數進行設置.室內環境是二維典型的三居室房間布局，如圖3 所示，包括兩個房間和一個走廊.A 區為實驗室，長8 m，寬6 m；B 區為走廊，長4 m，寬1.4 m；C 區為辦公室，長6 m，寬4 m.根據穩定性條件，設置網格剖分大小為 Δx=Δy=0.2 m，因此三個場景分別占據30×40、7×20 和20×30 個網格，共1 558 個網格點.組合場景由不規則混凝土墻壁包圍，墻壁的電導率和相對介電常數分別為 σ=0.06和εr=6.4，墻壁厚度一般為24 cm，因此設置墻壁占據一層網格.墻壁外部區域填充的是空氣，最外圍由UPML 包圍，作為電磁仿真的吸收邊界.

圖3 房間模型參數設置Fig.3 Parameter settings for the room model

在神經網絡訓練過程中，訓練數據對于神經網絡的訓練至關重要，也直接影響了訓練生成的網絡對于處理新數據的準確性.本文利用MATLAB 進行編程，產生發射信號，利用時域有限差分(finitedifference time-domain，FDTD)法仿真出輻射源發射信號到接收點進行采集的傳播過程.設置目標位于室內不同位置，輻射源輻射利用隨機產生的m序列調制的2PSK 信號，同時接收點記錄目標位置和采集接收數據，形成訓練數據集.

2.1.1 輻射信號設置

對于接收站持續采集的信號，我們需要保證在輸入層輸入的訓練數據中含有包含目標位置的有效信息，即保證輸入的訓練數據中應盡可能多地包含發射信號經過目標反射后的散射回波以及經過多次反射、散射后的多徑信號，使得位于遠場的接收站能夠接收更多的目標位置相關信息.

本文采用的輻射信號是目前數據通信中常用的2PSK 調制信號，為了滿足傳輸數據的隨機性，這里采用m序列產生調制數據，以盡可能地考慮定位系統對數據通信的內容沒有任何限制和要求.

PSK 信號是一種常用信號，使用二進制的基帶信號來控制載波的相位，使載波的相位能夠反映出數字消息的特征，表達式如下：

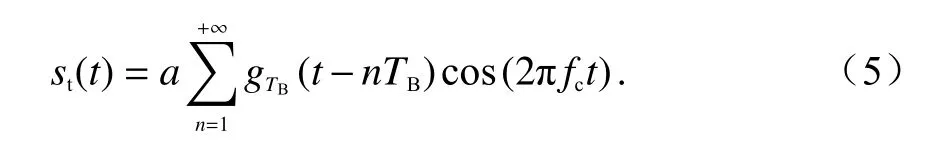
式中：a表示脈沖幅度；TB為矩形脈沖的持續時間；fc為載波信號的頻率.基帶信號(t)與高頻載波相乘，使得數字基帶信號能夠控制高頻載波的相位.

2.1.2 基于FDTD 的數據集獲取

FDTD 以差分原理為基礎，從麥克斯韋方程出發，直接將其轉化為差分方程，能夠在離散數值時空中仿真再現電磁波傳播的物理過程.其二維TM 波的差分方程迭代公式為：

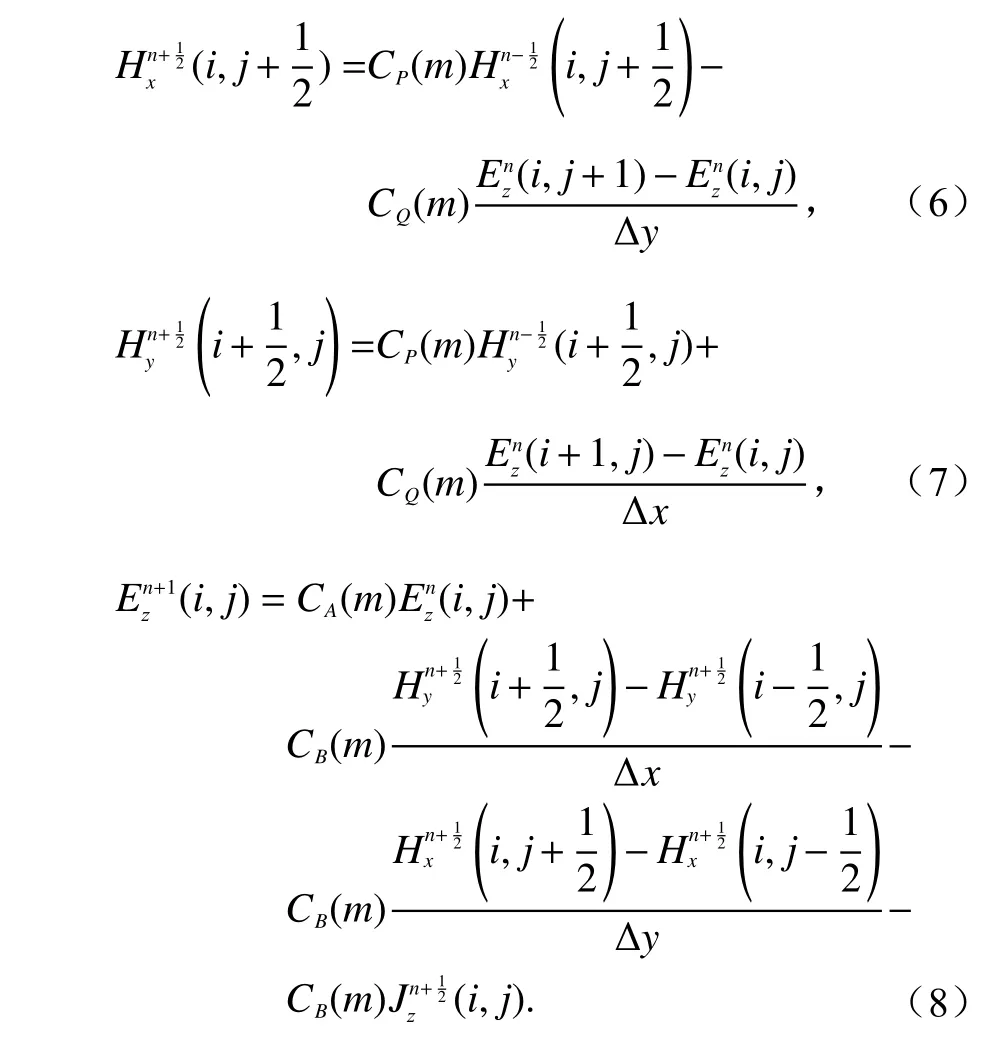
式中，CA(m),CB(m),CP(m),CQ(m)是與媒質參數和時間、空間網格大小有關的參數[13].

輻射信號用線電流源J模擬，由式(8)中引入進行激勵和輻射.

待定位目標假設是一個正方形的金屬散射體，占據3×3 個網格.在產生不同數據集樣本的過程中，將目標沿著室內場景的剖分網格按序移動，記錄其處于不同位置時對應的接收信號.在定位過程中，默認目標中心點坐標 (x,y)代表整個目標的位置，目標所占據網格的大小及整體位置坐標為

為保證離散后差分方程組的解是收斂和穩定的，離散麥克斯韋方程的穩定性和收斂性對時間和空間離散間隔有一定的限制.依據Courant 穩定性條件以及數值色散對空間離散間隔的要求，對空間離散 Δx、Δy，時間離散 Δt做出如下規定：

式中，λ表示信號的最小波長.

經過FDTD 迭代適當步數達到穩態后，記錄接收點場強數據作為我們的訓練輸入數據，記錄目標點位置作為輸出標簽數據.

利用FDTD 算法對圖3 所示室內場景結構進行仿真，得到的室內場強分布如圖4 所示.

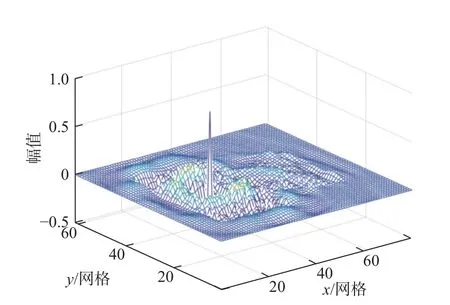
圖4 室內場強分布Fig.4 Distribution of indoor electrical field

由于室內的多徑反射，傳遞函數的復雜性，場強的空間分布信息非常豐富.

2.2 定位算法神經網絡的結構設計

依據信號的物理特征構建有效的神經網絡結構對算法至關重要.從多徑信號中提取目標位置信息，需要充分考慮多徑信號的時序特征，循環神經網絡是一個不錯的選擇，但循環神經網絡計算非常耗時，效果并不理想.

針對時序數據的這一特性，本文提出采用CNN來實現，利用卷積處理局部序列的前后關聯性和特征提取，將看似雜亂無章的接收信號轉換為蘊含信道傳遞規律的卷積結果.2PSK 信號經過多徑傳輸，由圖2 可以看出卷積是提取多徑信息的有效方法，但由于發射信號調制數據并非已知，而我們知道發射信號序列是由0、1 構成，也可以理解成由00、01、10、11 序列構成，進一步理解由000-111 構成.考慮到0、1 沒有碼元的過渡信息，000-111 八個卷積核對接收數據長度有一定要求，本文采用00、01、10、11 序列構成四個一維卷積核，實現對包含目標位置信息的信道特征進行提取.圖5 為圖3 場景下某一位置目標產生的接收信號與四個卷積核卷積后得到的結果.

圖5 接收信號與不同卷積核的卷積結果Fig.5 Convolution results of received signals with different convolution kernels

由圖5 可以看到，不同的卷積核卷積結果呈現不同的規律性.從物理意義上講，卷積結果體現了目標經過墻壁、目標反射散射后的時延變化特征，從而將時序信號中的時延信息轉換為體現空間分布情況的位置信息，然后利用全連接層，捕獲不同位置點的精細位置特征，最終實現室內精確定位.

CNN 結構如圖6 所示，神經網絡主要由兩部分構成：CNN 層、全連接層.

圖6 CNN 結構Fig.6 Structure of CNN

輸入層為接收傳感器接收到的一段N維時間序列x=[x1,x2,···,xN]，在輸入數據維數的選取上，為了使其充分含有信號傳播過程中的空間多徑信息，我們選取N=1 000，包含十個碼元長度和四十個載波周期.

在自定義卷積核的過程中，為了與發射的2PSK信號保持一致，卷積核中包含0 和1 兩種碼元信息，考慮到調制碼元含有信息及碼元長度的不同，決定CNN 層采用四個1×200 的卷積核.由于不同卷積核的卷積結果對應著不同的物理意義，需要充分保留卷積結果，因此將池化層大小設為1，不對卷積結果做出舍棄.

全連接層設計為兩層隱藏層，由于要解決的是室內定位問題，目標的位置坐標變化限制在一定范圍內，因此兩個隱層的激活函數分別設為ReLU 和Sigmoid；神經元個數分別設為1 024 和512；最終的輸出層結果y對應著目標所處位置的橫縱坐標，是一個回歸問題；輸出層采用線性激勵函數.

CNN 選用均方誤差(mean square error，MSE)作為代價函數，表達式為

式中：N為小批量樣本的樣本數量；y?(x)和y(x)分別為對目標的預測坐標及標簽坐標.

綜上所述，得到圖7 所示的訓練流程圖.

圖7 CNN 訓練流程Fig.7 The process of CNN training

3 實驗結果及分析

在實驗中，本文利用FDTD 方法產生神經網絡需要的訓練數據集和測試數據集，設置入射波為二維TM 波.針對不同情況，分別討論接收傳感器固定在室內和室外、室內環境存在噪聲、目標大小發生變化的定位情況.

3.1 實驗一

本節討論輻射源位于室內固定位置(25,30)，接收傳感器位于室內固定位置(58,38)時，利用神經網絡對室內目標的定位情況.

在數據集采集過程中，目標位于空間位置(x,y)處，輻射源持續發射信號，輻射信號采用m序列調制的2PSK 信號，載波設置為100 MHz.接收傳感器對信號進行接收.假設接收信號長度為Nt，神經網絡輸入維度N=1 000，記K=■Nt/N」，即目標每一處位置標簽(x,y)對應著接收信號的K組數據集.

我們將CNN 與普通全連接層神經網絡進行對比，觀察二者的定位效果.為了減少計算量，本文設置訓練小批量樣本大小為256，訓練輪數為100，學習率為0.008，優化器為Adam.

在定位耗費時間方面，主要對網絡的訓練耗時比較多，且與筆記本性能關系較大，筆記本型號是ThinkPad T14s,CPU 為AMD 銳龍7 PRO 4850U，集成顯卡.

目前數據集大小是312 620×1 000，1 000 為輸入長度，312 620 為數據組數.其中90%作為訓練集，10%作為測試集.利用CNN 訓練一輪的時間為3 min 左右，通常訓練二十幾輪網絡能夠基本收斂，可以根據所需要的定位精度確定訓練輪數.在網絡訓練結束后，我們對測試集內所有點進行定位，經過計時，三萬多組數據的測試集定位大概需要1 min.

設計對比試驗中的普通全連接層神經網絡，記為FC Net，其中含兩層隱藏層，第一層隱藏層1 200 個神經元，激活函數為ReLU；第二層隱藏層512 個神經元，激活函數為Sigmoid；其余參數設定同CNN.

表1 為兩種不同神經網絡測試結果.

表1 兩種神經網絡的測試結果Tab.1 Results of the two neural networks

圖8 為不同情況下的訓練和測試MSE 曲線.

圖8 訓練和測試MSE 曲線(室內單接收站)Fig.8 Training and test MSE curves(indoor single receiving station)

從實驗結果能夠明顯看出，相較于普通全連接層神經網絡，本文設計的組合CNN 具備更高的訓練效率和更好的訓練效果，僅利用普通神經網絡八分之一的訓練量，就達到了與其精度相差不大的訓練效果.在訓練數據量相當的情況下，CNN 訓練精度遠遠高于普通全連接層神經網絡.對于測試數據，該方法的平均坐標定位距離誤差為0.621 個網格，對應到空間實際平均定位距離誤差為12.42 cm.

經過分析，CNN 的優越性主要體現在，普通全連接層僅僅是對數據的訓練，而非建立在時序信號物理特性的基礎上進行的分析訓練.本文的發射信號是m序列調制的2PSK 信號，是四種碼卷積核形式信號的組合，經過空間中的多徑傳播，接收傳感器對其進行接收，二者通過卷積，即不斷滑動求和，能夠捕捉到各種多徑信號.卷積相關峰波動較大的地方，代表信號在空間傳播過程中遇到墻壁等障礙物引起的反射，導致相位發生突變.當與含有不同碼元信息的卷積核卷積時，這種相位的突變能夠體現室內環境的幾何結構，且由于不規則的墻壁構設、障礙物間的復雜相互作用，接收信號會包含攜帶目標精細幾何細節的信息，因此可以通過卷積從中訓練出有效位置信息.

3.2 實驗二

本實驗檢驗利用室外接收傳感器對室內目標的定位效果.實驗環境同實驗一，接收傳感器位于室外固定位置(57,15).

在本輪實驗中，利用CNN 進行訓練，本文設置K=203，訓練小批量樣本大小為256，訓練輪數為100，學習率為0.008，優化器設置為Adam.

由于訓練至30 輪時已基本收斂，下降幅度很小，因此取前30 輪代價函數值畫出變化曲線.圖9 為前30 輪的訓練和測試MSE 曲線.

由圖9 明顯看出，CNN 能夠有效學習接收信號中的位置信息，從而實現室外接收站對室內目標的精確定位.測試過程中，平均定位距離誤差為0.482 個網格，對應空間實際平均定位距離誤差為9.64 cm.

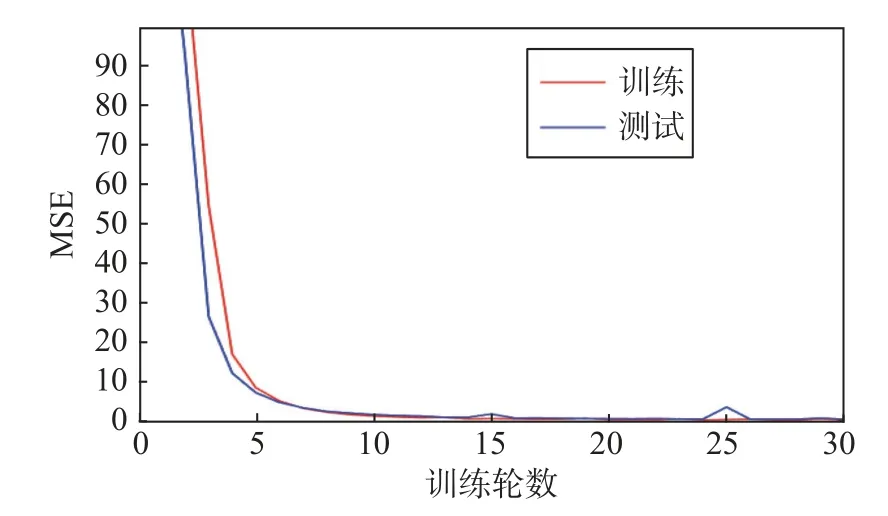
圖9 訓練和測試MSE 曲線(室外單接收站)Fig.9 Training and test MSE curves (outdoor single receiving station)

圖10 為分別利用訓練后網絡和測試接收數據集預測五個不同位置目標的定位分布圖.圖中紅色圓點為目標的位置標簽，散落在目標周圍的點為訓練后的網絡對目標的定位情況，顏色越淺，則定位坐標偏離目標位置越遠.從對同一位置目標的定位分布可以發現，通過該算法估計出的定位坐標均勻地分布在標簽周圍，即定位誤差方差較小，且每次定位精度較為穩定，能夠實現室外單接收站對室內目標的精確定位.

圖10 CNN 對任意目標位置的定位分布圖Fig.10 The location distribution of CNN towards targets at any position

3.3 實驗三

本實驗檢驗算法在不同信噪比條件下利用CNN 對目標的定位情況.實驗環境同實驗一.在實際環境中，或多或少地存在噪聲的影響，我們人為地在接收端加入高斯白噪聲，以模擬噪聲存在情況下的室內定位，觀察該方法在不同信噪比條件下對目標的定位情況.訓練過程中，利用CNN，設置K=203，訓練小批量樣本大小為256，訓練輪數為100，學習率為0.000 8，優化器為Adam.

表2 為不同信噪比下的定位情況.

表2 不同信噪比下的測試結果Tab.2 Results with different SNRs

通過對上述結果的分析，我們能夠實現對不同信噪比環境下利用單接收站實現對室內目標的精確定位，且信噪比越高，定位精度越高.

為了減少訓練次數，驗證網絡的泛化性，本文利用在室內理想無噪聲情況下的訓練網絡，實現對其他存在噪聲條件下的定位.當測試數據中信噪比為20 dB 時，對目標的平均定位距離誤差為3.812 個網格，對應空間實際平均定位距離誤差為76.24 cm；當測試數據中信噪比為30 dB 時，對目標的平均定位距離誤差為0.662 個網格，對應空間實際平均定位距離誤差為13.24 cm；當測試數據中信噪比為40 dB 時，對目標的平均定位距離誤差為0.43 個網格，對應空間實際平均定位距離誤差為8.6 cm.說明無噪聲理想環境下訓練的網絡對含噪聲信號定位具有一定的泛化性.經過分析，在對不同信噪比測試信號數據的定位過程中，卷積的過程相當于是滑動平均，能夠起到噪聲平滑的作用.同時可以看出，隨著信噪比降低，定位精度下降明顯，即定位算法對噪聲具有敏感性.信噪比在高于20 dB 情況下，算法仍然能夠得到比較滿意的定位精度.

3.4 實驗四

本實驗檢驗算法在待定位目標大小發生變化的情況下利用CNN 對目標的定位情況.實驗環境同實驗一.

首先由實驗一得到目標大小為3×3 個網格訓練好的網絡，利用該網絡結構對1×1 大小的目標進行定位測試.經過測試，平均定位距離誤差為6.378 個網格，對應空間實際平均定位距離誤差為1.276 m.

然后設置目標大小為1×1，產生訓練數據，并對其進行訓練，訓練環境同實驗一，網絡訓練MSE 為0.333，測試MSE 為2.488.利用訓練好的網絡結構對3×3 大小的目標進行定位測試，經過測試，平均定位距離誤差為5.359 個網格，對應空間實際平均定位距離誤差為1.072 m.

對以上測試結果進行分析，由于待定位目標大小發生變化，其產生散射場的等效電流發生變化，接收信號隨之發生變化，因此定位精度會受到影響.但在用訓練好的網絡對不同大小的目標進行定位時，本算法仍然能夠實現米級的定位精度，說明本算法對不同大小目標的定位具有一定的適應性，適用于對定位精度要求不高的情況下的粗略定位.

3.5 實驗五

本實驗檢驗算法在待定位目標大小發生變化的情況下利用CNN 對目標的定位情況.實驗環境在實驗一基礎上增設一個金屬柜，如圖11 所示.

圖11 室內場景示意圖(有金屬柜)Fig.11 Setting of room model parameter with a metal cabinet

金屬柜占據的網格坐標位置范圍為

在場景發生變化的情況下，需要對訓練數據集進行更新，利用FDTD 方法生成新的訓練集和測試集.訓練結果如下所示：訓練MSE 為0.076，測試MSE 為0.188，平均測試定位誤差為0.505 個網格，對應實際誤差為10.10 cm.

記室內房間沒有金屬柜的環境為場景A，室內房間增設金屬柜的環境為場景B，利用場景A 訓練的網絡對場景B 的測試數據進行測試，定位效果不甚理想.經過分析發現主要是因為在室內場景中放置金屬柜以后，對室內輻射源信號的傳播信道影響較大，導致其與場景A 下的空間傳播路徑區別很大，因此由場景A 訓練出的神經網絡節點間的權重和偏置相差很大，CNN 難以對場景B 的目標進行精確定位.

4 結 論

本文提出一種室內單站定位技術，利用CNN 對室內電波傳播的多徑效應構成的復雜信道信息進行學習，通過自定義卷積核，賦予神經網絡結構一定的物理意義，實現高效的精確定位.本文通過訓練實現了固定接收單傳感器位于室內和室外情況下的精確定位.

在單接收站位于室內時，能夠實現一個網格(0.2 m)內的精確定位，對測試數據的平均定位距離誤差為0.621 個網格(12.42 cm)；當單接收站位于室外時，測試數據的平均定位距離誤差為0.482 個網格(9.64 cm)；針對存在噪聲環境試驗發現，噪聲在信噪比高于20 dB 情況下，算法仍然能夠得到比較滿意的定位精度.該算法具備一定的抗噪聲性和泛化性，為室內定位提供了一種新的方法.本文是在二維相對理想條件下進行的算法設計，算法如何推廣到三維，以及適應不同大小的目標、目標的運動情況都需要進一步研究.