山區(qū)不等高多跨連續(xù)剛構(gòu)橋設計計算分析
王玲麗 蔡健
1.貴州省交通規(guī)劃勘察設計研究院有限公司 貴州 貴陽 550001 2.中交公路規(guī)劃設計院貴州分院 貴州 貴陽 550001
貴州高速為典型的山區(qū)公路,當橋位處地面起伏很大時,會出現(xiàn)同一座橋中各墩高度相差非常懸殊的情況。大墩高比下各墩的抗推剛度相差較多,邊主墩與中主墩須分別進行設計。根據(jù)李民偉、寧曉駿“不等高雙肢薄壁墩對大跨度連續(xù)剛構(gòu)靜力影響”[1]的結(jié)論,墩高比對橋梁上部結(jié)構(gòu)靜力影響相對較小,上部結(jié)構(gòu)可采用相同的剛束,橋墩可根據(jù)墩高比的不同,采用相同截面不同配筋或不同截面不同配筋的方法滿足規(guī)范要求。
多跨連續(xù)剛構(gòu)橋是墩梁固結(jié)的多次超靜定結(jié)構(gòu),在預應力、混凝土的收縮徐變、非設計合攏溫度下合攏等的作用下,橋墩中將產(chǎn)生較大的內(nèi)力,橋墩各肢的位移也有較大差別,上述不利情況可通過一定的措施得到改善,文中結(jié)合120m預應力混凝土連續(xù)剛構(gòu)橋為例,簡要介紹不等高多跨連續(xù)剛構(gòu)橋設計計算分析。
1 項目概況
該橋場區(qū)位于貴州西部高原山區(qū),受溶蝕影響,地形較為復雜。橋梁按路線分幅設計,主橋采用(65.5+120+120+65.5)m預應力混凝土連續(xù)剛構(gòu)橋,主墩高度左幅分別為46m、131m、80m,右幅分別為50m、131m、90m;過渡墩高度左幅為21m,右幅為30m。該橋左幅橋型布置圖如圖1所示。
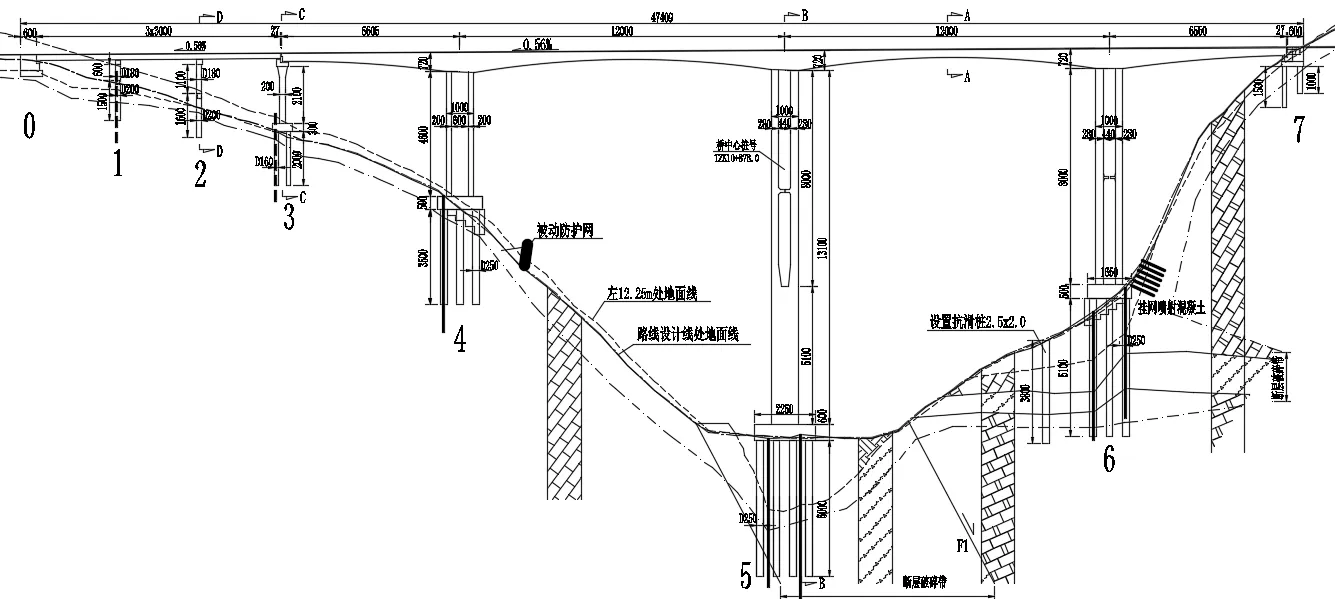
圖1 左幅橋型布置圖
2 主墩構(gòu)造設計
該橋主墩墩高相差懸殊,最矮的4號主墩左右幅墩高分為46m、50m,最高的5號主墩左右幅墩高均為131m,較高的6號主墩左右幅墩高分為80m、90m,最高墩與最矮墩的墩高比為2.85:1,較高墩與最矮墩的墩高比為1.8:1。計算發(fā)現(xiàn)邊主墩墩頂、底彎矩較大,抗裂計算較難通過,最高墩的墩底彎矩也較大,設計藉由減小邊墩的截面尺寸、增大中主墩剛度(中主墩采用上部雙肢薄壁、下部為箱形的組合結(jié)構(gòu))來改善受力,橋墩分別設計成三種結(jié)構(gòu)形式,最矮的4號主墩采用實心墩,最高的5號主墩采用上部雙肢薄壁、下部箱形的組合結(jié)構(gòu),較高的6號主墩采用雙肢薄壁空心墩。為保證箱梁0號塊橫隔板與橋墩的剛度匹配,箱梁的0號塊也設計成兩種形式,與實心墩相接的0號塊設置一道1.5m厚的橫隔板,與雙肢薄壁墩相接的0號塊設置兩道60cm厚的橫隔板,橫隔板間距1.6m。
橋墩細部構(gòu)造分別為:雙肢實心墩(橫向?qū)?.5m,縱向?qū)?.0m),兩片墩間凈距為6.0m,墩身不設系梁;薄壁空心墩與箱墩組合結(jié)構(gòu),上部80m高度范圍內(nèi)為雙肢薄壁空心墩(橫向?qū)?.5m,縱向?qū)?.8m),下部51m范圍內(nèi)為整體式箱墩(橫向?qū)?.5m,縱向?qū)?0m);雙肢薄壁空心墩(橫向?qū)?.5m,縱向?qū)?.8m),兩片墩間凈距為4.4m。為保證高墩在上部結(jié)構(gòu)懸臂澆筑施工時的穩(wěn)定性,在高墩墩身間設臨時系梁,系梁高0.8m,與墩身同寬,在上部箱梁合攏前予以移除。
3 主橋設計計算
以左幅橋為例建立計算模型,分述合攏順序、溫度作用、收縮徐變、合攏前頂推力對主墩的影響。
①合攏順序?qū)χ鞫盏挠绊懀翰捎靡韵聝煞N形式進行對比:1.先對稱合攏邊跨而后對稱合攏中跨;2.先對稱合攏中跨而后對稱合攏邊跨。兩種合攏方式對主墩墩頂及墩底彎矩、墩頂位移的影響見表1。
由表1可見,合攏順序?qū)χ鞫諒澗亍⒍枕斘灰频挠绊戄^小,可忽略不計。根據(jù)“高墩多跨連續(xù)剛構(gòu)橋合龍方案及合龍頂推力計算研究”[2]中的,“邊跨合龍后,由于邊支座摩擦力等因素,在次邊跨施加頂推力較難達到頂推邊墩的效果”[2],為此,該橋采用先中跨后邊跨的合攏順序。
②溫度作用對主墩的影響:該橋箱梁在23度下合攏,合攏溫度比設計溫度(15度)高8度,也就相當于全橋成橋后一直受到降溫8度的溫度力作用。降溫8度下各墩墩頂?shù)淖畲笪灰啤澗厝绫?所示(位移以向大樁號方向移動為正,向小樁號方向移動為負,彎矩以小樁號側(cè)受拉為正,大樁號側(cè)受拉為負)。
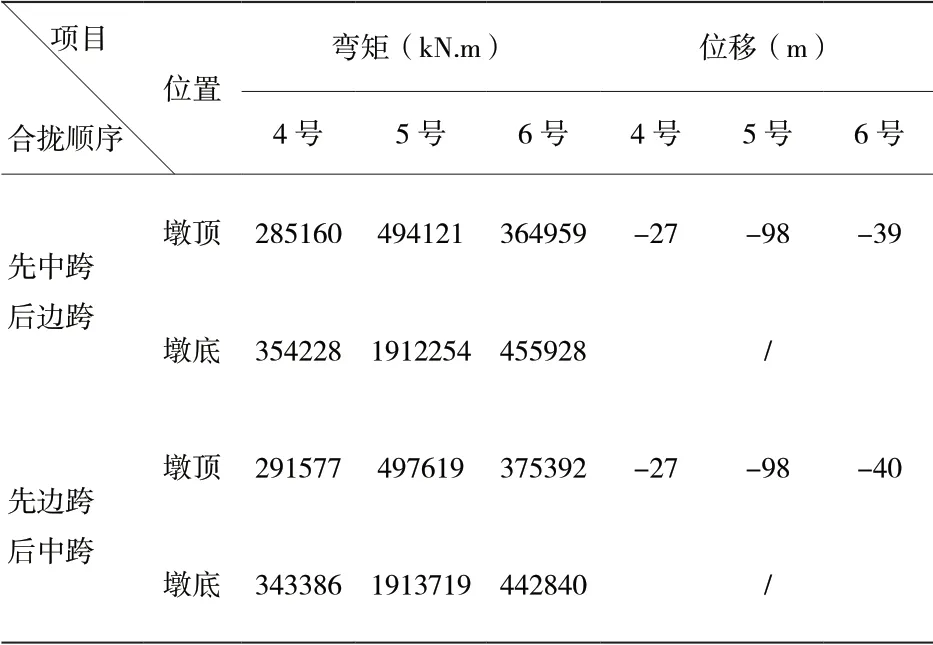
表1 不同合攏方式對各墩彎矩、位移的影響
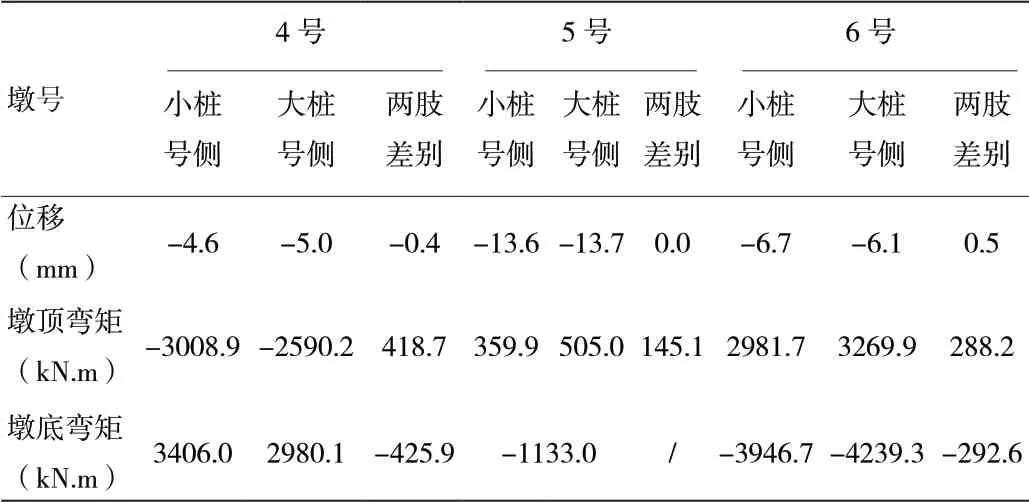
表2 降溫8度下各墩墩頂?shù)淖畲笪灰?/p>
由表中數(shù)據(jù)可知,降溫8度作用引起的各墩墩頂?shù)淖畲笪灰啤⒍枕數(shù)讖澗鼐^大,各墩均向小樁號方向偏移,橋墩各肢的位移相差不大,橋墩各肢的彎矩相差較大。
③收縮徐變對主墩的影響:剛成橋、成橋5年時、成橋10年時各墩的最大位移如表2所示,彎矩如表3所示。
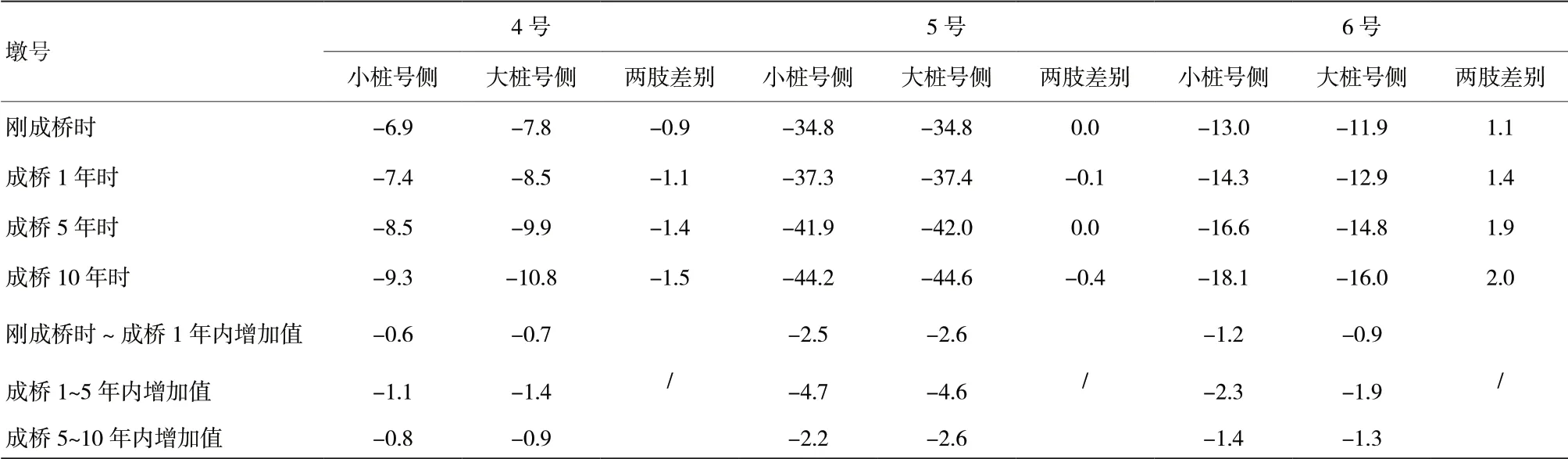
表3 各年各墩墩頂?shù)淖畲笪灰疲╩m)
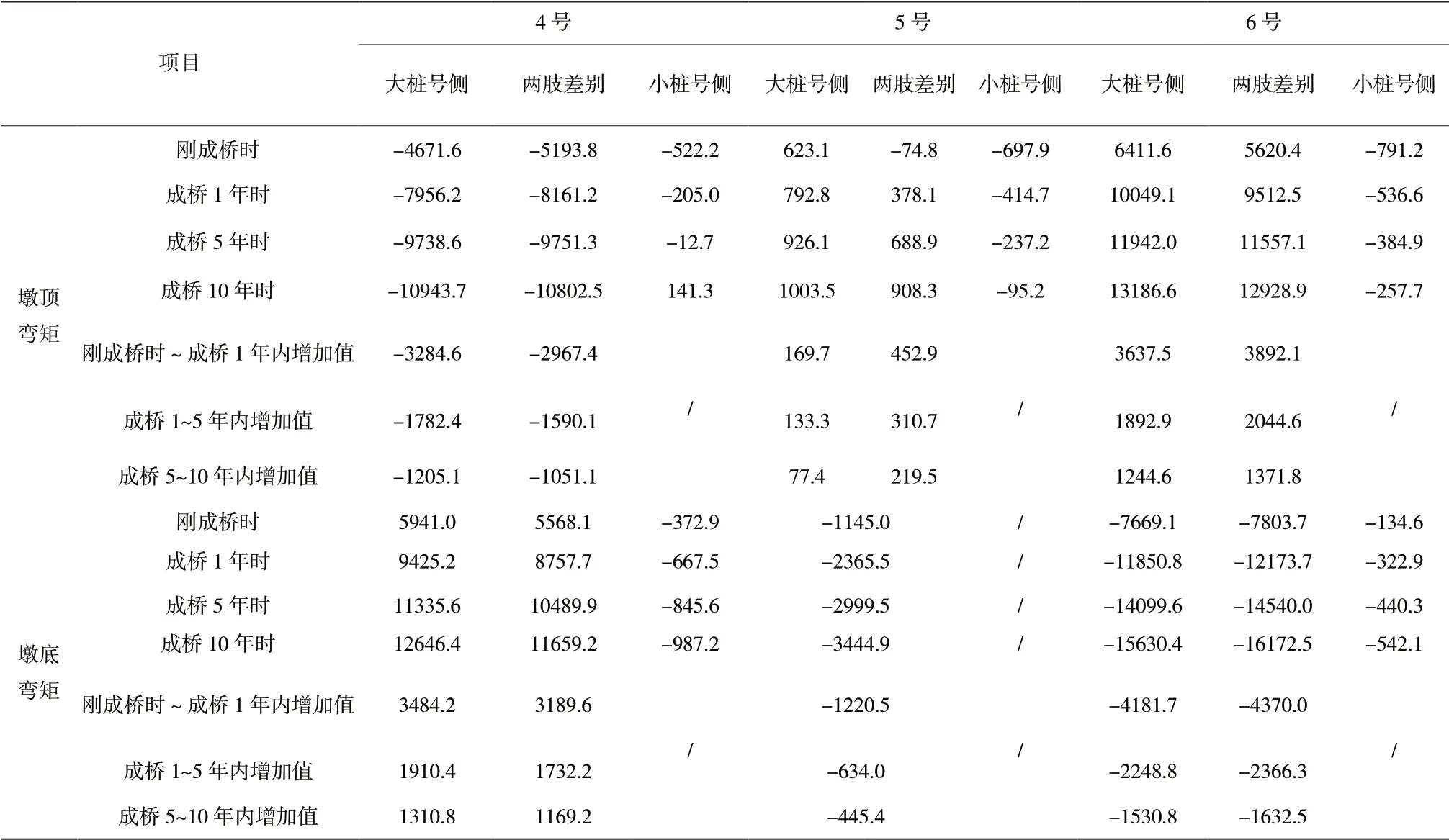
表4 各年各墩的彎矩(kN.m)
由表3可知,除5號墩剛成橋時及其后各年各肢的位移基本一致外,其余各墩各肢的位移均有一定的差別,且隨著時間增加差別越來越大。收縮徐變下各墩成橋1~5年內(nèi)的位移增加值最多,位移增加值在1.1mm以上,之后成橋5~10年內(nèi)位移增加值減少。
由表4可知,收縮徐變下各墩的彎矩增加較多,成橋1年內(nèi)的彎矩增加最多,其后各年的增加幅度逐漸減小,但趨勢上仍在增加。剛成橋時橋墩各肢的彎矩相差較大,收縮徐變下各肢墩頂彎矩的差別逐漸減少,墩底彎矩的差別逐漸增加。
④頂推對主墩的影響:為降低或消除混凝土的收縮徐變、非設計合攏溫度下合攏時留存在橋墩中的內(nèi)力,減小成橋后收縮徐變下各肢位移的差別,可于合攏前在合攏段兩側(cè)的箱梁上施加適當?shù)捻斖屏Γ鬼斖屏Ξa(chǎn)生的彎矩正好平衡混凝土的收縮徐變以及非設計合攏溫度下合攏引起的彎矩。假定橋墩中非設計合攏溫度下合攏時產(chǎn)生的彎矩為Md,各年混凝土的收縮徐變下的彎矩,第一年收縮徐變下的彎矩為M1、第二~五年收縮徐變下的彎矩為M2、第六~十年收縮徐變下的彎矩為M3,采用下面公式計算需平衡的彎矩M=Md+M1+0.9xM2+0.5xM3,為減少長期荷載在橋墩中產(chǎn)生的作用,對長期收縮徐變下的彎矩值進行了折減。通過試算求出需施加的頂推力的大小,在4、5號墩之間施加710kN的頂推力,在5、6號墩之間施加600kN頂推力,頂推后橋墩各年的位移、彎矩如表5、6所示。
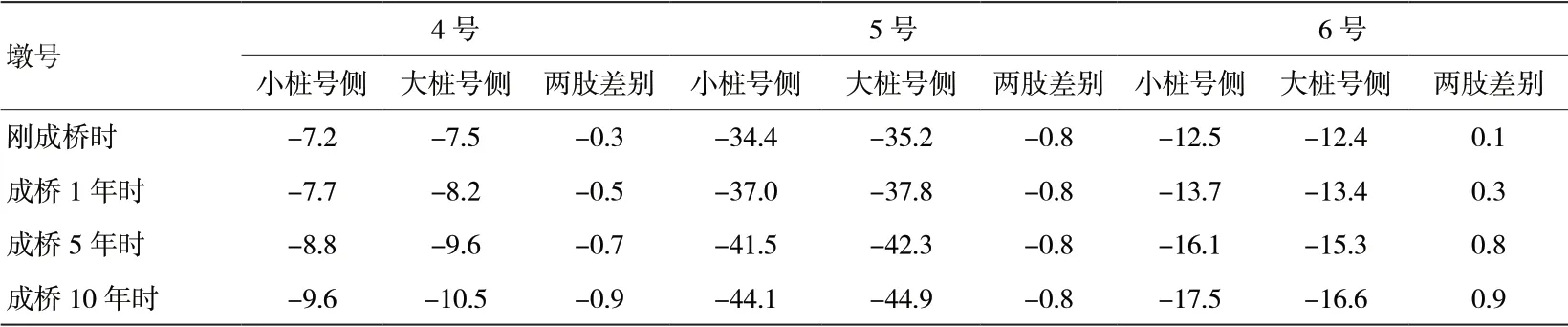
表5 頂推后各年各墩墩頂?shù)淖畲笪灰疲╩m)
對比表3、5可以看出,頂推后橋墩各年的位移與頂推前相差不多,但頂推后橋墩各肢的位移差別減小了。
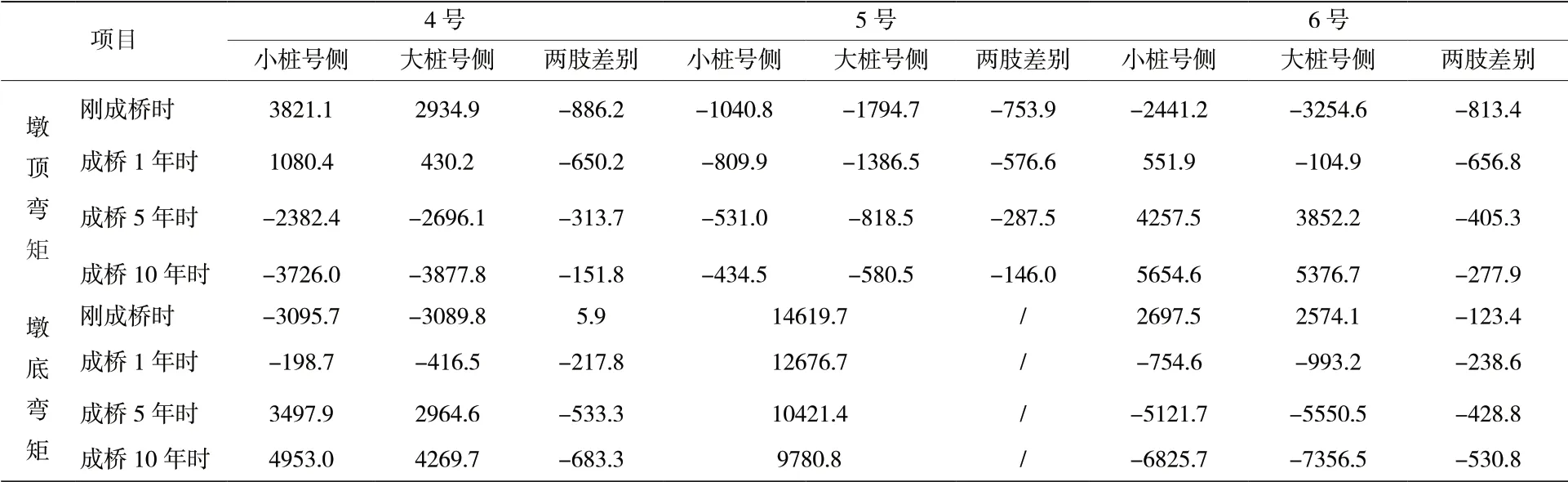
表6 頂推后各年各墩的彎矩(kN.m)
對比表4、6可以看出,頂推后4、6號墩各年的彎矩比頂推前大幅減少,頂推后成橋10年時這兩個橋墩的彎矩數(shù)值比頂推前減少50%以上,橋墩受力改善明顯,因為頂推后橋墩的彎矩方向與混凝土的收縮徐變產(chǎn)生的彎矩方向相反,隨著收縮徐變的增加,橋墩彎矩由上緣受拉變?yōu)橄戮壥芾ɑ蛴上戮壥芾優(yōu)樯暇壥芾W罡叩?號墩各年的彎矩比頂推前增加較多,但隨著時間的增加,增加值明顯減小。
頂推前收縮徐變下橋墩最大彎矩發(fā)生在較矮的橋墩墩底,頂推后收縮徐變下橋墩最大彎矩發(fā)生在最高的橋墩墩底,頂推改善了較矮橋墩的受力,同時受力較大的高墩,因為截面尺寸較大,設計計算比較容易滿足規(guī)范要求。
4 結(jié)束語
文中結(jié)合120m不等高多跨連續(xù)剛構(gòu)橋,簡要介紹了該橋的設計特點、上下部構(gòu)造設計,并得出如下結(jié)論:
1)大墩高比下各墩的抗推剛度相差較多,邊主墩與中主墩須分別進行設計。2)不同合攏順序?qū)χ鞫諒澗亍⒍枕斘灰频挠绊戄^小,可忽略不計,為減少邊支座摩擦力等因素的影響,采用先中跨后邊跨的合攏順序。3)由混凝土的收縮徐變、非設計合攏溫度下合攏等產(chǎn)生的永久內(nèi)力均較大,橋墩各肢的位移差別也較大,永久內(nèi)力、各肢的位移差別可通過合攏前的頂推得到改善。先計算不頂推時由混凝土的收縮徐變、非設計合攏溫度下合攏在橋墩中產(chǎn)生的彎矩,并進行適當?shù)慕M合,算出需要平衡的彎矩,而后通過試算求出頂推力的大小。

