質數、積數及“哥德巴赫猜想”
馮 浚
(甘肅省蘭州市稅務局 730070)
在數學領域,對數的基礎研究始終都沒有停止.對于質數,目前尚無較為簡明的類似偶數,奇數的數學表達式.鑒于此,可以從數最初的狀態入手,發現新的特性.
1 質數、積數
1.1 定義
1.1.1 質數的定義:正整數中,只能被1和自己整除的數為質數.
為了便于研究,用q表示質數.
故,在正整數中,按由小到大順序排列的質數是:1,2,3,5,7,11,…,對應表示為:q1,q2,q3,q4,q5,q6,….
1.1.2 積數的定義:正整數中,質數以外的數為積數.同理,用p表示積數.則p=m1×m2.
(1)
p稱為積數,m1,m2稱為因數(m1>1,m2>1);m1,m2若為質數,則稱為質因數;上式中最小的因數一定是質數,可稱其為最小質因數.如16=4×4=2×8.
則其因數為4,或2,8;最小因數為2,也為16的最小質因數.
1.2 表達式
1.2.1 積數的表達
根據質數,積數的特性,經邏輯推導,對最小質因數為qn的所有積數及qn,可用下列式子表示:
(2-1)
式(2-1)中,n=0,±1,±2,±3,…, 1≤n2≤(q2-1),1≤n3≤(q3-1),…,1≤nn-1≤(qn-1-1).
由于q2=2,q3=3,q4=5,q5=7,q6=11,…,qn,則n2=1,n3=1,2,n4=1,2,3,4,n5=1,2,3,4,5,6,n6=1,2,3,4,5,6,7,8,9,10,…nn-1=1,2,3,…,qn-1-1.
1.2.2 質數的表達
與(2-1)式同理,對1和所有大于qn的質數,以及最小質因數大于qn的所有積數,可用下式表示:
(2-2)
式(2-2)中,n=0,±1,±2,±3,… ,1≤n2≤(q2-1),1≤n3≤(q3-1),…,1≤nn≤(qn-1).
由于:q2=2,q3=3,q4=5,q5=7,q6=11,…,qn,則n2=1,n3=1,2,n4=1,2,3,4,n5=1,2,3,4,5,6,n6=1,2,3,4,5,6,7,8,9,10,…nn=1,2,3,…,qn-1.
1.3 負積數,負質數
根據正,負數的特點,為了便于研究,計算等,引入負積數,負質數概念.
A,則式(2-1)積數的表達為
(2-3)
式(2-3)中,n=0,±1,±2,±3,…,1≤n2≤(q2-1),1≤n3≤(q3-1),…,1≤nn-1≤(qn-1-1).
由于q2=2,q3=3,q4=5,q5=7,q6=11,…,qn,則n2=1,n3=1,2,n4=1,2,3,4,n5=1,2,3,4,5,6,n6=1,2,3,4,5,6,7,8,9,10,…nn-1=1,2,3,…,qn-1-1.
舉例如下:
(1)當最小質因數為2時,即qn=q2=2 ,n1=q1-1=1-1=0 ;則:P2=q2!n
n=0,±1,±2,±3,…,
n=0,±1,±2,±3,…,n2=1.

n=0,±1,±2,±3,…,n2=1,n3=1,2.
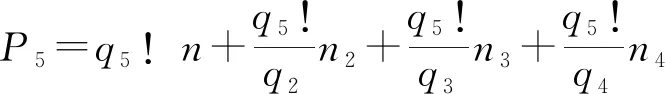
n=0,±1,±2,±3,…,n2=1,n3=1,2,n4=1,2,3,4.

n=0,±1,±2,±3,…,n2=1,n3=1,2,n4=1,2,3,4,n5=1,2,3,4,5,6,B,則式(2-2)質數的表達為
(2-4)
式(2-4)中,n=0,±1,±2,±3,…
1≤n2≤(q2-1),1≤n3≤(q3-1),…,1≤nn≤(qn-1).
由于:q2=2,q3=3,q4=5,q5=7,q6=11,…,qn
則:n2=1,n3=1,2,n4=1,2,3,4,n5=1,2,3,4,5,6,n6=1,2,3,4,5,6,7,8,9,10,…nn=1,2,3,…,qn-1.
舉例如下:

n=0,±1,±2,±3,…,n2=1.

n=0,±1,±2,±3,…,n2=1,n3=1,2.
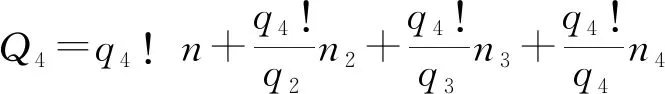
n=0,±1,±2,±3,…,n2=1,n3=1,2,n4=1,2,3,4.

n=0,±1,±2,±3,…,n2=1,n3=1,2,n4=1,2,3,4,
n5=1,2,3,4,5,6.

n=0,±1,±2,±3,…,n2=1,n3=1,2,n4=1,2,3,4,n5=1,2,3,4,5,6,n6=1,2,3,4,5,6,7,8,9,10.
1.4 首數集
1.4.1 積數首數集
分析式(2-3)可得,PN是由若干個等差數列組成.而最小質因數的不同,則等差數列的數量也不相同.
在式(2-3)中,所有大于0并且小于qn!(即:0∠PN∠qn!)的數稱之為首數,并且所有的首數組成首數集,用Bn表示.
則式(2-3)可用下式表示:
PN=qn!n+Bn
(3-1)
式(3-1)中,n=0,±1,±2,±3,….
由此可以得出結論一:qn及最小質因數為qn的所有積數,可組成若干個公差為qn!的等差級數.即其可用若干個公差為qn!的等差級數表示.
其中,最小數為qn,次之為(qn)2.
舉例如下:
(1)最小質因數由2開始,當最小質因數為2時,qn=q2=2 ,qn!=q2!=1*2=2,n1=q1-1=1-1=0 ;則:B2=0;P2=q2!+B2=1*2n+0=2n.故q2時,q2!=2,B2=0,P2=2n.即偶數表達式P2=2n,可表述為:其為2及最小質因數為2的所有積數.

P3=q3!n+B3=1*2*3*n+3=6n+3故q3時,q3!=6,B3為:3,P3=6n+3
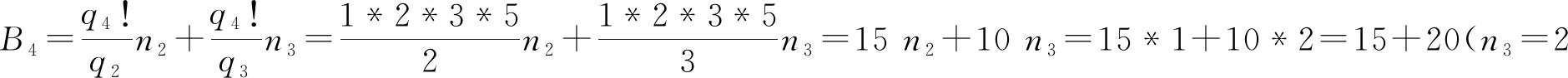
由于q4!為30,即公差為30;故調整后B4為:5,25,故q4時,q4!= 30,B4為:5, 25 (即B4=5,25)
P4=30n+5,30n+25

由于q5!為210,即公差為210;故調整后B4為:203,161,119,77,133,91,49,7,即7,49,77,91,119,133,161,203.故q5時,q5!= 210,B5為:7,49,77,91,119,133,161,203,P5=210n+7,210n+49,210n+77,210n+91,210n+119,210n+133,210n+161,210n+203,即P5=210n+{7,49,77,91,119,133,161,203}.
1.4.2 質數首數集
同理,在式(2-4)中,所有大于0并且小于qn!(即:0∠QN∠qn!)的數稱之為首數,并且所有的首數組成首數集,用An表示.
則式(2-4)可用下式表示:
QN=qn!n+An
(3-2)
式(3-2)中,n=0,±1,±2,±3,….
由此可以得出結論二:1和所有大于qn的質數,以及最小質因數大于qn的所有積數,可組成若干個公差為qn!的等差級數.即其可用若干個公差為qn!的等差級數表示.
其中,最小數為1,次之為qn+1;最小積數p為(qn+1)2.
舉例如下:
(1)當q2時,即qn=q2=2時,
對1和所有大于2的質數,以及最小質因數大于2的所有積數如下:
qn=q2=2,qn!=q2!=1*2=2,n2=q2-1=2-1=1;

Q2=q2!n+A2=1*2n+1=2n+1
故q2時,q2!=2,A2=1,Q2=2n+1.
即奇數表達式Q2=2n+1,可表述為:其為1和大于2的所有質數,以及最小質因數大于2的所有積數的總和.
(2)q3時,即qn=q3=3時,
對1和所有大于3的質數,以及最小質因數大于3的所有積數如下:
qn=q3=3,qn!=q3!=1*2*3=6,n2=1,n3=1,2;
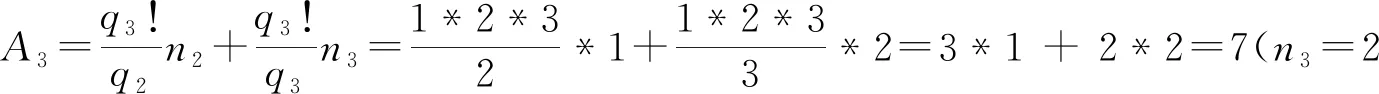
由于q3!為6,即公差為6;故調整后A3為:1, 5;故:q3時,q3!=1*2*3=6,A3為:1, 5(即A3=1, 5)Q3=6n+1,6n+5
(3)q4時,即qn=q4=5時,對1和所有大于5的質數,以及最小質因數大于5的所有積數如下:
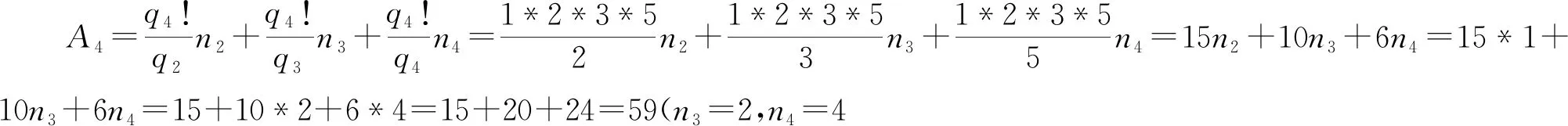
及:15+10*2+6*3
=53(n3=2,n4=3時)
=47(n3=2,n4=3時)
=41(n3=2,n4=1時)
=49(n3=1,n4=4時)
=43(n3=1,n4=3時)
=37(n3=1,n4=2時)
=31(n3=1,n4=1時)
由于q4!為30,即公差為30;
故調整后A4為:1,7,11,13,17,19,23,29
故:q4時,q4!=1*2*3*5=30,
A4為:1,7,11,13,17,19,23,29
Q4=30n+1,30n+7,30n+11,30n+13,30n+17,30n+19,30n+23,30n+29
即Q4=30n+{1,7,11,13,17,19,23,29}
(4)q5時,即qn=q5=7時,
對1和所有大于7的質數,以及最小質因數大于7的所有積數如下:
qn=q5=7,qn!=q5!=1*2*3*5*7=210,
n2=1,n3=1,2,n4=1,2,3,4,n5=1,2,3,4,5,6;

=105n2+70n3+42n4+30n5=105*1+70*2+42*4+30*6=105+140+168+180
=593(n3=2,n4=4,n5=6時)
及.….…(分別帶入具體數值,此處略)
由于q5!為210,即公差為210;
故調整后A5為1,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97,101,103,107,109,113,121,127,131,137,139,143,149,151,157,163,167,169,173,179,181,187,191,193,197,199,209.
故q5時,q5!=1*2*3*5*7=210,
A5為:1,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97,101,103,107,109,113,121,127,131,137,139,143,149,151,157,163,167,169,173,179,181,187,191,193,197,199,209.
Q5=q5!n+A5=210n+{1,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97,101,103,107,109,113,121,127,131,137,139,143,149,151,157,163,167,169,173,179,181,187,191,193,197,199,209.}
1.4.3 質數首數集與積數首數集之間的邏輯關系
在QN中,對于An,其開始連續qn+1級的等差數列,為An+1和Bn+1.
舉例如下:
q3時,即qn=q3=3,qn+1=q4=5,q3!=6;B3為:3;P3=6n+3;A3為:1,5;
Q3=6n+1,6n+5
A3開始連續q4級(即5級)的等差數列具體為:
1,7,11,13,19,25
5,11,17,23,25,29,
則A4為:1,7,11,13,17,19,23,29;
B4為:5,25.
2 質數、積數的有關特性和規律
之前,對于質數做了基本的分類.即:在正整數中,按由小到大順序排列的質數是:1,2,3,5,7,11,…,對應表示為:q1,q2,q3,q4,q5,q6,…qn….
將具體相關數值帶入各表達式中,分析研究可初步得到一些規律和特性,即積數表達式與質數表達式的邏輯關系等等.特別是首數集非常重要,其為質數,積數的重要基礎和內容,其特性和規律在某種意義上也是質數,積數的特性和規律.
在此,可將質數等做進一步分類.
2.1 初步分類及基本特性
2.1.1 常質數:數值1存在于任意An中,可將1稱為常質數.
2.1.2 基楚質數:分析表達式(3-2)等,可將q1,q2,q3,q4,q5,q6,…qn稱為基楚質數.
并且,通過已知的基楚質數,應用式(3-2)等可以求出更大更多的基楚質數.
結論三:通過已得出的基楚質數,可求出小于任意一個數的所有質數.即:可以求出任意大的所有質數.
2.1.3 對稱分布情況:
(1),Pn,Bn,Qn,An相對于0對稱分布.
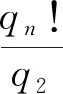

2.2 質數,積數的有關特性和規律
2.2.1 以上表達式帶入具體數值后如下:
(1)q1時,即qn=q1=1時,為常質數.Pn及Qn相同,為:n.
(2)q2時,即qn=q2=2時,q2!=2,
B2為0,P2=2n;其為偶數表達式.
A2為1,Q2=2n+1;其為奇數表達式.
則此時,基楚質數為2,
(3)q3時,即qn=q3=3時,q3!=6,B3為:3,
P3=6n+3
A3為1,5
Q3=6n+1,6n+5
具體為1,7,11,13,19,25,︱31,…6n+1
5,11,17,23,25,29,︱35,…6n+5
則此時,基楚質數為2,3,
(4)q4時,即qn=q4=5時,q4!=30,B4為:5,25
P4=30n+5,30n+25
具體為5,35,65,95,125,…30n+5
25,55,85,115,145,…30n+25
A4為:1,7,11,13,17,19,23,29
Q4=30n+{1,7,11,13,17,19,23,29}
具體為:

則此時,基楚質數為2,3,5,(qn+1)2=(q5)2=49
故:7,11,13,17,19,23,29,31,37,41,43,47均為質數(結論二).
(5)q5時,即qn=q5=7時,q5!=210,
B5為:7,49,77,91,119,133,161,203,
P5=210n+{7,49,77,91,119,133,161,203}
具體為:

A5為:1,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97,101,103,107,109,113,121,127,131,137,139,143,149,151,157,163,167,169,173,179,181,187,191,193,197,199,209.
Q5=q5!n+A5=210n+{1,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97,101,103,107,109,113,121,127,131,137,139,143,149,151,157,163,167,169,173,179,181,187,191,193,197,199,209.}
具體為:

則此時,基楚質數為2,3,5,7,(qn+1)2=(q6)2=121
故:11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97,101,103,107,109,113均為質數(結論二).
2.2.2 有關特性和規律
(1)在QN中,設任意一個數Qm;則Qm=qn!nm+Am,若Qm為因數是qm的積數,則Qm一定能被qm整除;并且,在QN中,存在Qm+n,nm+n=(nm+nn).即Qm+n=qn!nm+n+Am=qn!(nm+nn)+Am=qn!nm+Am+qn!nn
當nn是qm的倍數時,Qm+n也一定是因數為qm的積數.
結論四:在QN中,對于任意一個因數為qm的積數Qm,在其所在的等差數列中,相對于Qm其等差數是其qm的整數倍時,其一定是因數為qm的積數,并且只有其是因數為qm的積數.當qm為qn+1時,其一定是最小質因數為qn+1的積數.
由于在QN中,所有積數的最小質因數是qn+1,故:在QN中,任一公差為qn!的等差數列,在連續qn+1項中只有一個最小質因數為qn+1的積數.
(2),對于QN,可進一步分為QN+1和PN+1.
即:對1和所有大于qn的質數,以及最小質因數大于qn的所有積數,可進一步分為:1和所有大于qn+1的質數,以及最小質因數大于qn+1的所有積數,即:QN+1;和最小質因數為qn+1的所有積數(含qn+1),及PN+1.即:QN=QN+1+PN+1
(3),在QN中,最小質因數為qn+1的所有積數在QN中占比最大,占QN全體的qn+1分之一;所占比例遞減的積數分別是最小質因數為qn+2,qn+3,qn+4,…的積數.
并且,在QN中,
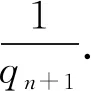
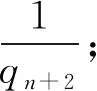

…
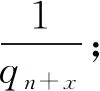
結論五:qn越大,其積數在QN中所占比例越小.
3 關于“哥德巴赫猜想”
哥德巴赫1742年給歐拉的信中哥德巴赫提出了以下猜想:任一大于2的偶數都可寫成兩個質數之和.但是一直無法證明.
現就質數,積數和偶數等進一步分析研究如下.
3.1 偶數與兩個質數之差
由以上可得:
3.1.1 在QN中,對于任意兩個數Ax,Ay;此兩數之差為Xn,在其所在的等差數列中,此兩數同時加,減相同數量的公差,其相對應的兩數之差均滿足此條件,即兩數之差同樣為Xn;所以在QN中有無數組數滿足此條件.
即Xn=Ax-Ay=qn!nAx-qn!nAy
舉例如下:
(1),q3時,即qn=q3=3時,q3!=6,基楚質數為2,3;
B3為:3,P3=6n+3
A3為:1,5
Q3=6n+1,6n+5
具體為:1,7,11,13,19,25,︱31,…6n+1
5,11,17,23,25,29,︱35,…6n+5
設:Ax=23,Ay=7;
則:X3=23-7=16
X3=16=qn!nAx-qn!nAy=n6*23-n6*7
即:Q3中,17-1,及23-13,35-19,41-25…均為16.
(2)q4時,即qn=q4=5時,q4!=30,基楚質數為2,3,5,
B4為:5,25
P4=30n+5,30n+25
A4為:1,7,11,13,17,19,23,29
Q4=30n+{1,7,11,13,17,19,23,29}
具體為:

設Ax=23,Ay=11;
則X4=23-11=12
X4=12=qn!nAx-qn!nAy=n30*23-n30*11
即Q4中,23-11,53-41,83-71,113-101…均為12.
3.1.2 在QN中,對于任意兩個數Ax,Ay;此兩數之差為Xn,在其同時連續qn+1級的等差數列中,其相對應的在QN+1中,有(qn+1-2)組滿足此條件,另外2組分別是:Ax為最小質因數是qn+1的積數和Ay為最小質因數是qn+1的積數的一組.
舉例如下:
q3時,即qn=q3=3時,q3!=6,基楚質數為2,3;qn+1=q4=5;B3為:3,P3=6n+3
A3為:1,5
Q3=6n+1,6n+5
設:Ax=23,Ay=7;
則:X3=23-7=16
X3=16=qn!nAx-qn!nAy=n6*23-n6*7
即:Q3中,其同時連續5級的等差數列為:(23,7),(29,13),(35,19),(41,25),(47,31).
其相對應的在Q4中,有3組滿足此條件,分別是(23,7),(29,13),(47,31).另外兩組不在Q4中的是Ax為最小質因數是5的積數,即積數為35的一組(35,19)和Ay最小質因數是5的積數,即積數為25的一組(41,25).
3.1.3 在QN中,對于任意兩個數Ax,Ay;此兩數之差為Xn.
(1),當QN大于等于Q2時,由于其中所有的數均為奇數,故Xn一定是偶數.
(2),當:q3時,即qn=q3=3時,q3!=6,基楚質數為2,3;B3為:3,P3=6n+3
A3為:1,5
Q3=6n+1,6n+5
具體為:1,7,11,13,19,25,︱31,…6n+1
5,11,17,23,25,29,︱35,…6n+5
在Q3中,對于任意兩個數Ax,Ay;此兩數之差為偶數X3,在其同時連續q4級(即5級)的等差數列中,對于Ax-Ay(即X3大于0小于等于6,即0 滿足X3為2的有5組. 即X3=Ax-Ay=2時,有5組, 如(5,7),(11,13),(17,19),(23,25),(29,31); 滿足X3為4的有5組. 即X3=Ax-Ay=4時,有5組, 如(1,5),(7,11),(13,17),(19,23),(25,29); 滿足X3為6的有10組. 即X3=Ax-Ay=6時,有10組, 如(1,7),(7,13),(13,19),(19,25),(25,31),(5,11),(11,17),(17,23),(23,29),(29,35); 對于Ax-Ay(即X3)大于6,即6 由于任意一個大于6的偶數,均可用:6n+2,6n+4,6n,這三種情況之一表示; 故在Q3中,對于兩個數Ax,Ay;此兩數之差可為任意一個偶數X3,同理,在其同時連續q4級(即5級)的等差數列中,至少有5組滿足此條件.當X3為6n+2或6n+4時,有5組;當X3為6n時,有10組. 例如:滿足X3為8的有5組. 即X3=Ax-Ay=8=6+2時,有5組, 為(5,13),(11,19),(17,25),(23,31),(29,37); 滿足X3為10的有5組. 即X3=Ax-Ay=10=6+4時,有5組, 為(1,11),(7,17),(13,23),(19,29),(25,35); 滿足X3為12的有10組. 即X3=Ax-Ay=12=6+6=2*6時,有10組, 為(1,13),(7,19),(13,25),(19,31),(25,37),(5,17),(11,23),(17,29),(23,35),(29,41); (3),q4時,即qn=q4=5時,q4!=30,基楚質數為2,3,5, B4為:5,25;P4=30n+5,30n+25 A4為:1,7,11,13,17,19,23,29 Q4=30n+{1,7,11,13,17,19,23,29} 由于在Q3中,對于任意兩個數Ax,Ay;此兩數之差X3可以是任意一個偶數.同時,由于在Q3中,在其同時連續q4級(即5級)的等差數列中,其相對應的在Q4中,至少有3組滿足此條件. 故在Q4中,對于兩個數Ax,Ay;此兩數之差同樣可以是任意一個偶數.同時,在其同時連續q5級(即7級)的等差數列中,至少有7組滿足此條件.其相對應的在Q5中,至少有5組滿足此條件. 以此類推,可以得出結論六:在QN中,對于兩個數Ax,Ay;此兩數之差Xn可以是任意一個偶數.即:對于任意一個偶數,可以由無數組QN中的兩數之差表示. 3.1.4 對于任意一個偶數,在QN中,有無數組兩個數之差滿足此條件(結論六).而QN越大, 在QN中,質數占比越小(結論五).則在QN中無數組兩個數之差滿足此條件的,并且同為質數的比例越大. 所以可以得出結論七:對于任意一個偶數,可以由無數組兩個質數相減表示. 3.2.1 在QN及An中,質數和積數的有關情況一 (1)對于Qx,Ax的前qx+1項的總和為Ax+1+Bx+1. 例如,對于Q5,A5的前q6項的總和為A6+B6. (2)對于Qx中,所有積數的最小質因數為qx+1. … 舉例如下: 對于Q5中,所有積數的最小質因數為q6. … (3)在Qx中,由于在以上積數占比的計算中都包含最小質因數,并且各積數均大于或等于其最小質因數的平方.所以,在Qx中,Ax的前qx+1項的總和中,同一最小質因數的積數在其中的實際占比小于或等于其算數平均占比. 對于Qx,在Ax的前qx+1項的總和中, … 3.2.2 在QN及An中,質數和積數的有關情況二 (1)對于式(3-2),即QN=qn!n+An;具體為:Q3=q3!n+A3,即Q3=6n+A3 Q4=q4!n+A4,即Q4=30n+A4 Q5=q5!n+A5,即Q5=210n+A5 Q6=q6!n+A6,即Q6=2310n+A6 Q7=q7!n+A7,即Q7=30030n+A7 Q8=q8!n+A8,即Q8=510510n+A8 對于式(3-1),即PN=qn!n+Bn;具體為:P3=q3!n+B3,即P3=6n+B3 P4=q4!n+B4,即P5=30n+B4 P5=q5!n+B5,即P5=210n+B5 P6=q6!n+B6,即P6=2310n+B6 P7=q7!n+B7,即P7=30030n+B7 P8=q8!n+B8,即P8=510510n+B8 … (2)按照以上算式進行計算得出如下: 對于Q3,Q3=q3!n+A3,即Q3=6n+A3;在A3的前q4項的總和中,積數只有最小質因數為q4的積數.其占比用Z3表示為:0.2. 對于Q4,Q4=q4!n+A4,即Q4=30n+A4;在A4的前q5項的總和中,積數為最小質因數為q5到q7的積數.積數算數平均占比(總和)用Z4表示約為:0.23836. 對于Q5,Q4=q5!n+A5,即Q5=210n+A5;在A5的前q6項的總和中,積數為最小質因數為q6到q16的積數.積數算數平均占比(總和)用Z5表示約為:0.27186. 對于Q6,Q6=q6!n+A6,即Q6=2310n+A6;在A6的前q7項的總和中,積數為最小質因數為q7到q41的積數.積數算數平均占比(總和)用Z6表示約為:0.25060. 對于Q7,Q7=q7!n+A7,即Q7=30030n+A7;在A7的前q8項的總和中,積數為最小質因數為q8到q128的積數.積數算數平均占比(總和)用Z7表示約為:0.24440. 對于Qn,在An的前qn+1項的總和中,積數算數平均占比(總和)用Zn表示;若以Y軸為Zn,X軸為Qn,則其關系如下: 由此具體分析如下: 對于Q3和Q4,其屬于開始階段,在Ax的前qx+1項的總和中,由于部分因素未出現,其不能完全吻合總體特性和規律.但自Q5后,各種因素的出現,故其可顯示總體特性和規律.即:對于Qx,在Ax的前qx+1項的總和中,所有積數算數平均占比(總和)在出現峰值0.27186后,其趨勢為逐漸緩慢下降. 并且,由此可得推斷一:對于Qx,在Ax的前qx+1項的總和中,所有積數算數平均占比(總和)均處于較低的占比,且遠低于50%. 3.2.3 證明 由結論七可得:任意一偶數Xn,則在QN中,存在Ax,Ay,滿足:Xn=Ax-Ay(0 當qn! 對于Xn,Ax,Ay,也滿足:Xn=(Ax-mqn-1!)-(Ay-mqn-1!);(m=1,2,3,…) 當m1qn-1!開始大于Ay起,(Ay-m1qn-1!)<0,此時,Xn實際為兩數相加.并且自此起到(m2+1)qn-1!開始大于Ax起的前1級,即0<(Ax-m2qn-1!),{Ax-(m2+1)qn-1!}<0時,至少有qn組滿足此(由于qn! 例如:Xn=104,則q4! m1=4,m2=21, 即Xn=(127-4*6)-(23-4*6)=103+1 Xn=(127-5*6)-(23-5*6)=97+7 Xn=(127-6*6)-(23-6*6)=91+13 … Xn=(127-20*6)-(23-20*6)=7+97 Xn=(127-21*6)-(23-21*6)=1+103 共18組. (1)當Xn≤q4!,即Xn≤30時, 可代入具體數值計算證明:Xn均可由一組以上兩個質數相加表示. 即:Xn=qx+qy (2)當q4! 存在Xn=(Ax-mq3!)-(Ay-mq3!)=(Ax-m*6)-(Ay-m*6)(m=1,2,3,…) 即Xn=(Ax-m1*6)-(Ay-m1*6)=(Ax-m1*6)+(m1*6-Ay) Xn={Ax-(m1+1)6}+{(m1+1)6-Ay} Xn={Ax-(m1+2)6}+{(m1+2)6-Ay} … Xn=(Ax-m2*6)+(m2*6-Ay) 滿足等式,并且等式右邊兩數均大于0的至少有q4組,即至少有5組. 而在這些組中,包含q4分之一的為最小質因數是q4的積數;故在這些組中,即:在此至少5組中,包含5分之一的為最小質因數是5的積數;所以在這些組中,至少有3組為:“在A4的前7項的總和”中的數.由于其積數算數平均占比(總和)小于50%(Z4約為:0.23836);所以其中至少有一組兩數均為質數.并且具體計算也可證明. 例如,例如Xn=32,則q4! 也滿足:Xn=(Ax-mq3)-(Ay-mq3)=(43-m*6)-(11-m*6) m1=2,m2=7, 即Xn=(43-2*6)-(11-2*6)=31+1 Xn=(43-3*6)-(11-3*6)=25+7 Xn=(43-4*6)-(11-4*6)=19+13 Xn=(43-5*6)-(11-5*6)=13+19 Xn=(43-6*6)-(11-6*6)=7+25 Xn=(43-7*6)-(11-7*6)=1+31 共6組. 最小質因數是5的積數的組為:(25,7)和(7,25);在A4的前7項的總和中的數有4組,為(31,1),(19,13),(13,19),(1,31);并且均為質數. (3)當q5! 存在Xn=(Ax-mq4!)-(Ay-mq4!)=(Ax-m*30)-(Ay-m*30)(m=1,2,3,…) 即Xn=(Ax-m1*30)-(Ay-m1*30)=(Ax-m1*30)+(m1*30-Ay) Xn={Ax-(m1+1)30}+{(m1+1)30-Ay} Xn={Ax-(m1+2)30}+{(m1+2)30-Ay}… Xn=(Ax-m2*30)+(m2*30-Ay) 滿足等式,并且等式右邊兩數均大于0的至少有q5組,即7組. 而在這些組中,包含q5分之一的為最小質因數是q5的積數;故在這些組中,即:在而此至少7組中,包含7分之一的為最小質因數是7的積數;所以在這些組中,至少有5組為:“在A5的前11項的總和”中的數.由于其積數算數平均占比(總和)小于50%(Z5約為:0.27186);所以其中至少有一組兩數均為質數. 例如,例如:Xn=210,則q5! 也滿足:Xn=(Ax-mq4)-(Ay-mq4)=(212-m*30)-(11-m*30) m1=1,m2=7, 即Xn=(223-1*30)-(11-1*30)=193+19 Xn=(223-2*30)-(11-2*30)=163+49 Xn=(223-3*30)-(11-3*30)=133+79 Xn=(223-4*30)-(11-4*30)=103+109 Xn=(223-5*30)-(11-5*30)=73+139 Xn=(223-6*30)-(11-6*30)=43+169 Xn=(223-7*30)-(11-7*30)=13+199 共7組. 最小質因數是7的積數的組為:(163,49)和(133,79);在A5的前11項的總和中的數有5組,為(193,19),(103,109),(73,139),(43,169),(13,199);并且兩數均為質數的有4組,為(193,19),(103,109),(73,139),(13,199). (4)當qn! 存在Xn=(Ax-mqn-1!)-(Ay-mqn-1!) (m=1,2,3,…) 即Xn=(Ax-m1qn-1!)-(Ay-m1qn-1!) Xn=(Ax-m1qn-1!)+(m1qn-1!-Ay) Xn={Ax-(m1+1)qn-1!}+{(m1+1)qn-1!-Ay} Xn={Ax-(m1+2)qn-1!}+{(m1+2)qn-1!-Ay} … Xn=(Ax-m2qn-1!)+(m2qn-1!-Ay) 注:m1,m2滿足:0<{Ay-(m1-1)qn-1!},(Ay-m1qn-1!)<0; 并且0<(Ax-m2qn-1!),{Ax-(m2+1)qn-1!}<0. 滿足等式右邊兩數均大于0的至少有qn組. 而在這些組中,包含qn分之一的為最小質因數是qn的積數;故在這些組中,至少有其總組數減二組(最少是q4! 所以可以得出結論八:對于任意一個偶數,可以由一組以上兩個質數相加表示. 3.3.1 在正整數的范圍內: 對于任意一個偶數,可以由無數組兩個質數相減表示;并且也可以由一組以上兩個質數相加表示. 3.3.2 引入負質數概念后,為: 對于任意一個大于零的偶數,可以由無數組兩個質數相加表示;其中兩個質數均大于零情況至少有一組.3.2 偶數與兩個質數之和




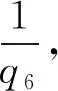
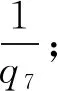
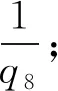





3.3 綜合以上可歸納如下

